A 3D elastic micropolar model of vertebral trabecular bone from lattice homogenization of the bone microstructure

Abstract

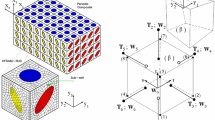
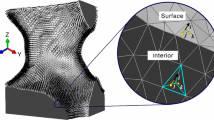
A 3D anisotropic micropolar continuum model of vertebral trabecular bone is presently developed accounting for the influence of microstructure-related scale effects on the macroscopic effective properties. Vertebral trabecular bone is modeled as a cellular material with an idealized periodic structure made of open 3D cells. The micromechanical approach relies on the discrete homogenization technique considering lattice microrotations as additional degrees of freedom at the microscale. The effective elastic properties of 3D lattices made of articulated beams taking into account axial, transverse shearing, flexural, and torsional deformations of the cell struts are derived as closed form expressions of the geometrical and mechanical microparameters. The scaling laws of the effective moduli versus density are determined in situations of low and high effective densities to assess the impact of the transverse shear deformation. The classical and micropolar effective moduli and the internal flexural and torsional lengths are identified versus the same microparameters. A finite element model of the local architecture of the trabeculae gives values of the effective moduli that are in satisfactory agreement with the homogenized moduli.

Appendix: homogenized elastic rigidities of the 3D hexagonal orthotropic lattice

The elastic constants in the homogenized stiffness matrix express versus the geometrical and micromechanical parameters of the unit cell as follows:

$$\begin{aligned} {E}_{11}&= \frac{E_{s} \pi {r}^{2}C_{t} \left( {3LE_{s} {r}^{2}C_{t}^{2} +L^{3}C_{t}^{2} G_{s} {k}_{s} +3Lr^{2}G_{s} k_{s} +6hr^{2}G_{s} k_{s} -3Lr^{2}C_{t}^{2} {G}_{s} {k}_{s}} \right) }{L_{v} \left( {h+LS_{t}} \right) \left( {6r^{2}C_{t}^{2} hG_{s} k_{s} +3E_{s} r^{2}L+G_{s} k_{s} {L}^{3}+2hL^{2}G_{s} k_{s} +6hr^{2}E_{s} -2L^{2}hC_{t}^{2} G_{s} k_{s} -6E_{s} hr^{2}C_{t}^{2} } \right) }; \\ E_{12}&= E_{21} =\frac{E_{s} \pi r^{2}C_{t} S_{t} \left( {3E_{s} r^{2}+G_{s} k_{s} L^{2}-3r^{2}G_{s} k_{s}} \right) }{L_{v} \left( {6r^{2}C_{t}^{2} hG_{s} k_{s} +3E_{s} r^{2}L+G_{s} k_{s} {L}^{3}+2hL^{2}G_{s} k_{s} +6hr^{2}E_{s} -2L^{2}hC_{t}^{2} G_{s} k_{s} -6E_s hr^{2}C_t^{2}} \right) }; \\ E_{22}&= -\frac{E_{s} \pi r^{2}\left( {h+LS_t } \right) \left( {-G_{s} k_{s} L^{2}+3E_{s} r^{2}C_t^{2} +G_{s} k_{s} L^{2}C_{t}^{2} -3r^{2}G_{s} k_{s} C_{t}^{2} -3E_{s} {r}^{2}} \right) }{LL_{v} C_{t} \left( {6r^{2}hG_{s} k_{s} C_{t}^{2} +3E_{s} {r}^{2}L+G_{s} k_{s} L^{3}+2hL^{2}G_{s} k_{s} +6hr^{2}E_{s} -2L^{2}hG_{s} k_{s} C_{t}^{2} -6E_{s} hr^{2}C_{t}^{2} } \right) };\\ E_{13}&= E_{31} =E_{23} =E_{32} =0;E_{33} =\frac{E_s \pi r^{2}}{LC_t \left( {h+LS_{t} } \right) };\\ E_{44}&= -\frac{3}{2}\frac{E_{s} \pi r^{4}G_{s} k_{s} C_{t} \left( {\begin{array}{l} -6h^{2}E_{s} r^{2}-3r^{2}h^{2}G_{s} k_{s} -3L^{2}r^{2}G_{s} k_{s} + 6C_{t}^{2} L^{2}E_{s} r^{2}-4S_{t} hL^{3}G_{s} k_{s} \\ -2C_{t}^{2} Lh^{3}G_{s} k_{s} -6C_{t}^{2} LhE_{s} {r}^{2}-3C_{t}^{2} h^{2} E_{s} r^{2}+3C_{t}^{2} r^{2}h^{2}G_{s} k_{s} -6L^{2}E_{s} r^{2} \\ +2L^{4}C_{t}^{2} G_{s} k_{s} -2G_{s} k_{s} L^{4}-12LhS_{t} E_{s} r^{2}-6LhS_{t} r^{2}G_{s} k_{s} -L^{2}h^{2}C_{t}^{2} G_{s} k_{s} -2L^{2}h^{2}G_{s} k_{s} \\ \end{array}} \right) }{L_{v} \left( {G_{s} k_{s} L^{2}+3E_{s} r^{2}} \right) \left( {\begin{array}{l} 3S_{t} L^{3}r^{2}G_{s} k_{s} -3Lr^{2}C_{t}^{2} S_{t} h^{2}G_{s} k_{s} +9S_{t} Lr^{2}h^{2}G_{s} k_{s} +6C_{t}^{2} S_{t} hr^{2}L^{2}E_{s} +C_{t}^{2} S_{t} h^{2}L^{3}G_{s} k_{s} \\ +3r^{2}h^{2}LC_{t}^{2} S_{t} E_{s} +2C_{t}^{2} S_{t} h^{3}L^{2}G_{s} k_{s} -3C_{t}^{2} h^{3}r^{2}G_{s} k_{s} +h^{3}L^{2}G_{s} k_{s} +2h^{4}LC_{t}^{2} G_{s} k_{s} \\ +3C_{t}^{2} h^{3}E_{s} ^{2}+3h^{3}G_{s} k_{s} r^{2}+9hL^{2}r^{2}G_{s} k_{s} +6h^{2}LC_{t}^2 r^{2}E_{s} -6r^{2}C_{t}^2 hL^{2}G_{s} k_{s} \\ \end{array}} \right) };\\ E_{45}&= -\frac{3}{2}\frac{E_{s} \pi r^{4}G_{s} k_{s} C_{t} \left( {\begin{array}{l} -6h^{2}E_{s} r^{2}L-6L^{3}E_{s} r^{2}-3C_{t}^2 r^{2}h^{2}LG_{s} k_{s} +2C_{t}^2 L^{2}h^{3}G_{s} k_{s} +3C_{t}^2 h^{2}E_{s} r^{2}L-2L^{5}G_{s} k_{s} \\ -4S_{t} hL^{4}G_{s} k_{s} +3r^{2}h^{2}LG_{s} k_{s} -2L^{3}h^{2}G_{s} k_{s} +3L^{3}r^{2}G_{s} k_{s} +6h^{3}C_{t}^2 E_{s} r^{2} \\ +6L^{3}C_{t}^2 E_{s} r^{2}+C_{t}^2 L^{3}h^{2}G_{s} k_{s} -12S_t L^{2}hE_s r^{2}+6S_t r^{2}hL^{2}G_{s} k_{s} +2L^{5}C_{t}^2 G_{s} k_{s} \\ \end{array}} \right) }{L_{v} \left( {G_{s} k_{s} L^{2}+3E_{s} r^{2}} \right) \left( {\begin{array}{l} 3S_{t} L^{3}r^{2}G_s k_s -3Lr^{2}C_t^2 S_t h^{2}G_s k_s +9S_t Lr^{2}h^{2}G_{s} k_{s} +6C_{t}^2 S_{t} hr^{2}L^{2}E_{s} +C_{t}^2 S_{t} h^{2} L^{3}G_{s} k_{s} \\ +3r^{2}h^{2}LC_{t}^2 S_{t} E_{s} +2C_{t}^2 S_{t} h^{3}L^{2}G_{s} k_{s} -3C_{t}^2 h^{3}r^{2}G_{s} k_{s} +h^{3}L^{2}G_{s} k_{s} +2h^{4}LC_{t}^2 G_{s} k_{s} \\ +3C_{t}^2 h^{3}E_{s} r^{2}+3h^{3}G_{s} k_{s} r^{2}+9hL^{2}r^{2}G_{s} k_{s} +6h^{2}LC_{t}^2 r^{2}E_{s} -6r^{2}C_{t}^2 hL^{2}G_{s} k_{s} \\ \end{array}} \right) };\\ E_{54}&= \frac{3}{2}\frac{E_s \pi r^{4}G_s k_s \left( {\begin{array}{l} 3S_t C_t^2 r^{2}h^{2}G_s k_s -3h^{2}r^{2}S_{t} G_{s} k_{s} +2G_{s} k_{s} L^{4}S_{t} C_{t}^2 -2S_{t} C_{t}^2 h^{3}LG_{s} k_{s} +6L^{2}S_{t} {C}_{t}^2 E_{s} r^{2}-S_{t} C_{t}^2 L^{2}h^{2}G_{s} k_s \\ -6S_{t} C_{t}^2 hLE_{s} r^{2}-3S_{t} C_{t}^2 h^{2}E_{s} r^{2}-3L^{2} r^{2}S_{t} G_{s} k_{s} +6LhC_t^2 r^{2}G_{s} k_{s} +2G_{s} k_{s} L^{3}hC_{t}^2 +6LhC_{t}^2 E_{s} r^{2} \\ -6Lr^{2}hG_{s} k_{s} \\ \end{array}} \right) }{L_{v} LC_{t} \left( {G_s k_s L^{2}+3E_s r^{2}} \right) \left( {\begin{array}{l} 6r^{2}LhS_{t} G_{s} k_{s} +3r^{2}h^{2}C_{t}^2 E_{s} +h^{2}L^{2}C_{t}^2 G_{s} k_{s} +3r^{2}h^{2}G_{s} k_{s} \\ +6LhC_{t}^2 E_{s} r^{2}+2C_{t}^2 h^{3}LG_{s} k_{s} +3L^{2}r^{2}G_{s} k_{s} -3C_{t}^2 h^{2}r^{2}G_{s} k_{s} \\ \end{array}} \right) };\\ E_{55}&= \frac{3}{2}\frac{E_s \pi r^{4}G_s k_s \left( {\begin{array}{l} C_{t}^2 S_{t} L^{2}h^{2}G_{s} k_{s} -3S_{t} C_{t}^2 r^{2}h^{2}G_{s} k_s + 2S_{t} Lh^{3}C_{t}^2 G_{s} k_{s} +6C_{t}^2 S_{t} L^{2}E_{s} r^{2}+3r^{2}h^{2} S_{t} G_{s} k_{s} +2S_{t} C_{t}^2 L^{4}G_{s} k_{s} \\ +3L^{2}S_{t} r^{2}G_{s} k_{s} +3C_{t}^2 S_{t} h^{2}E_{s} r^{2}+6S_{t} C_{t}^2 hE_{s} r^{2}L-6LhC_{t}^2 r^{2}G_{s} k_{s} +2G_{s} k_{s} L^{3}hC_{t}^2 +6LhC_ {t}^2 E_{s} r^{2} \\ +6Lr^{2}hG_{s} k_{s} \\ \end{array}} \right) }{L_{v} LC_{t} \left( {G_{s} k_{s} L^{2}+3E_{s} r^{2}} \right) \left( {\begin{array}{l} 6r^{2}LhS_{t} G_{s} k_{s} +3r^{2}h^{2}C_{t}^2 E_{s} +h^{2}L^{2}C_{t}^2 G_{s} k_{s} +3r^{2}h^{2}G_{s} k_{s} \\ +6LhC_{t}^2 E_{s} r^{2}+2C_{t}^2 h^{3}LG_{s} k_{s} +3L^{2}r^{2}G_{s} k_{s} -3C_{t}^2 h^{2}r^{2}G_{s} k_{s} \\ \end{array}} \right) };\\ E_{66}&= \frac{3}{2}\frac{E_{s} \pi r^{4}G_{s} k_{s} \left( {\begin{array}{l} 6S_{t} hE_{s} r^{2}L_{v} +9S_{t} LE_{s} r^{2}L_{v} +L_{v}^2 h^{2}S_{t} G_{s} k_{s} -3L^{2}S_{t} C_{t}^2 E_{s} r^{2}+2S_{t} h^{3}L_{v} G_{s} k_{s} \\ +3L^{3}S_{t} L_{v} G_{s} k_{s} +3E_{s} r^{2}h^{2}S_{t} +S_{t} L^{2} L_{v}^2 G_{s} k_{s} -L_{v}^2 S_{t} L^{2}C_{t}^2 G_{s} k_{s} +3S_{t} L^{2}E_{s} r^{2} \\ +6hE_{s} r^{2}L_{v} -6LhC_{t}^2 E_{s} r^{2}-2LhL_{v}^2 C_{t}^2 G_s k_{s} +6LhE_{s} r^{2}+2LhL_{v}^2 G_{s} k_{s} +2L^{2}hL_{v} G_{s} k_{s} \\ \end{array}} \right) }{L_{v} LC_{t} \left( {G_{s} k_{s} L^{2}+ 3E_s r^{2}} \right) \left( {\begin{array}{l} 2LhS_t L_v^2 G_s k_s +6LhS_t E_s r^{2}+L^{3}G_s k_s L_v +3h^{2}E_s r^{2}+3L^{2}E_s r^{2}+3E_s r^{2}LL_v \\ +2h^{3}L_v G_s k_s +6hE_s r^{2}L_v +h^{2}L_v^2 G_s k_s +L^{2}L_v^2 G_s k_s -3L^{2}C_t^2 E_s r^{2}-L^{2}C_t^2 L_v^2 G_s k_s \\ \end{array}} \right) };\\ E_{67}&= \frac{3}{2}\frac{E_s \pi r^{4}G_s k_s \left( {\begin{array}{l} L^{3}S_{t} L_{v} G_{s} k_{s} -6S_{t} hE_{s} r^{2}L_{v} +3S_{t} LE_{s} r^{2} L_{v} +S_{t} L_{v}^2 L^{2}C_{t}^2 G_{s} k_{s} -2S_{t} h^{3}L_{v} G_{s} k_{s} \\ +3S_{t} L^{2}C_{t}^2 E_{s} r^{2}-S_{t} L^{2}L_{v}^2 G_{s} k_{s} -3E_{s} r^{2}h^{2}S_{t} -3S_{t} L^{2}E_{s} r^{2}-L_{v}^2 h^{2}S_{t} G_{s} k_{s} \\ +2L^{2}hL_{v} G_{s} k_{s} +2LhL_{v}^2 C_{t}^2 G_{s} k_{s} +6LhC_t^{2} E_s r^{2}+6hE_{s} r^{2}L_{v} -6LhE_s r^{2}-2LhL_v^{2} G_{s} k_{s} \\ \end{array}} \right) }{L_{v} LC_{t} \left( {G_{s} k_{s} L^{2} +3E_s r^{2}} \right) \left( {\begin{array}{l} 2LhS_{t} L_{v}^{2} G_{s} k_{s} +6LhS_{t} E_{s} r^{2}+L^{3}G_{s} k_{s} L_{v} +3h^{2}E_{s} r^{2} \\ +3L^{2}E_{s} r^{2}+3E_{s} r^{2}LL_v +2h^{3}L_{v} G_{s} k_{s} +6hE_s r^{2}L_v \\ +h^{2}L_v^2 G_{s} k_{s} +L^{2}L_{v}^2 G_{s} k_{s} -3L^{2}C_{t}^2 E_{s} r^{2}-L^{2}C_{t}^2 L_{v}^2 G_{s} k_{s} \\ \end{array}} \right) };\\ E_{76}&= -\frac{3}{2}\frac{E_s \pi r^{4}G_s k_s \left( {\begin{array}{l} -2LhL_v^2 S_{t} G_{s} k_{s} -6LhS_{t} E_{s} r^{2}+2h^{3}L_{v} G_{s} k_{s} -3L^{2}E_{s} r^{2}+3E_{s} r^{2}LL_{v} +L^{3}G_{s} k_{s} L_{v} \\ +6hE_{s} r^{2}L_{v} -L^{2}L_{v}^2 G_{s} k_{s} -3h^{2}E_{s} r^{2}-{h}^ {2}L_{v}^2 G_{s} k_{s} +3L^{2}C_{t}^2 E_{s} r^{2}+{L}^{2}C_{t}^2 L_{v}^2 G_{s} k_{s} \\ \end{array}} \right) }{LC_{t} \left( {G_{s} k_{s} L_{v}^2 +3E_{s} r^{2}} \right) \left( {\begin{array}{l} 2h^{4}L_{v} G_{s} k_{s} +h^{3}L_v^{2} G_{s} k_{s} +S_{t} L^{4}L_v G_s k_{s} +9hL^{2}E_{s} r^{2}+hL^{3}L_{v} G_{s} k_{s} \\ +9S_{t} h^{2}E_{s} r^{2}L+S_{t} L^{3}L_{v}^2 G_s k_{s} +3S_{t} L^{3} E_{s} r^{2}-S_{t} {C}_t^2 L^{3}{L}_{v}^2 G_{s} k_{s} -3S_{t} C_{t}^2 L^{3}E_s r^{2} \\ -3C_{t}^2 hL^{2}L_{v}^2 G_{s} k_{s} -9C_t^2 hL^{2}E_{s} r^{2}+2S_{t} Lh^{3}L_{v} G_{s} k_{s} +3L^{2}S_{t} E_{s} r^{2}L_{v} +3hE_{s} r^{2}LL_{v} \\ +3h^{3}E_{s} r^{2}+3hL^{2}L_{v}^2 G_{s} k_{s} +6LhS_{t} E_{s} r^{2} L_{v} +3S_{t} h^{2}L_{v}^2 LG_{s} k_{s} +6E_{s} L_{v} r^{2}h^{2} \\ \end{array}} \right) };\\ \end{aligned}$$

$$\begin{aligned} E_{77}&= \frac{3}{2}\frac{E_{s} \pi r^{4}G_{s} k_{s} \left( {\begin{array}{l} 18LhS_{t} E_{s} r^{2}+6LhL_{v}^2 S_{t} G_{s} k_{s} +3h^{2}L_v^2 G_{s} k_{s} +L^{3}G_{s} k_{s} L_{v} +3E_{s} r^{2}LL_{v} +3L^{2}L_{v}^2 G_{s} k_{s} \\ +9h^{2}E_{s} r^{2}+6hE_{s} r^{2}L_{v} +2h^{3}L_{v} G_{s} k_{s} +9L^{2}E_{s} r^{2}-3L^{2}C_{t}^2 L_{v}^{2} G_{s} k_{s} -9L^{2}C_{t}^2 E_{s} r^{2} \\ \end{array}} \right) }{LC_{t} \left( {G_{s} k_{s} L_{v}^2 +3E_{s} r^{2}} \right) \left( {\begin{array}{l} 2h^{4}L_{v} G_{s} k_{s} +h^{3}L_{v}^2 G_{s} k_{s} +S_{t} L^{4}L_v G_s k_{s} +9hL^{2}E_{s} r^{2}+hL^{3}L_{v} G_{s} k_{s} \\ +9S_{t} h^{2}E_{s} r^{2}L+S_{t} L^{3}L_{v}^2 G_{s} k_{s} +3S_{t} L^{3} E_{s} r^{2}-S_{t} C_{t}^2 L^{3}L_{v}^2 G_{s} k_{s} -3S_{t} C_{t}^2 L^{3}E_s r^{2} \\ -3C_{t}^2 hL^{2}L_{v}^2 G_{s} k_{s} -9C_t^2 hL^{2}E_s r^{2}+2S_t Lh^{3}L_v G_s k_s +3L^{2}S_t E_s r^{2}L_v +3hE_s r^{2}LL_v \\ +3h^{3}E_s r^{2}+3hL^{2}L_v^2 G_s k_s +6LhS_t E_s r^{2} L_v +3S_t h^{2}L_v^2 LG_s k_s +6E_s L_v r^{2}h^{2} \\ \end{array}} \right) };\\ E_{88}&= \frac{3}{2}\frac{E_s \pi r^{4}G_s k_s \left( {9C_t^2 E_s r^{2}L+3C_{t}^2 L_{v}^2 LG_{s} k_{s} +L^{2}G_{s} k_{s} L_{v} +3E_{s} r^{2}L_{v} } \right) }{LC_{t} \left( {G_{s} k_{s} L_{v}^2 +3E_{s} r^{2}} \right) \left( {h+LS_{t} } \right) \left( {3C_{t}^2 E_{s} r^{2}L+C_{t}^2 L_{v}^2 LG_s k_s +L^{2}G_s k_s L_v +3E_s r^{2}L_v } \right) }; \\ E_{89}&= -\frac{3}{2}\frac{E_s \pi r^{4}G_s k_s \left( {L^{2}G_{s} k_{s} L_{v} -C_{t}^2 L_{v}^2 LG_{s} k_{s} -3C_{t}^2 E_{s} r^{2}L +3E_{s} r^{2}L_{v} } \right) }{LC_{t} \left( {G_{s} k_{s} L_{v}^2 +3E_{s} r^{2}} \right) \left( {h+LS_{t} } \right) \left( {3C_{t}^2 E_{s} r^{2}L+C_{t}^{2} L_{v}^{2} LG_{s} k_{s} +L^{2}G_{s} k_{s} L_{v} +3E_{s} r^{2}L_v } \right) }; \\ E_{98}&= \frac{3}{2}\frac{E_{s} \pi r^{4}G_{s} k_{s} C_{t} \left( {L^{2}G_{s} k_{s} L_{v} -C_{t}^2 L_{v}^2 LG_{s} k_{s} -3C_{t}^2 E_{s} r^{2} L+3E_{s} r^{2}L_{v} } \right) }{L_{v} \left( {G_{s} k_{s} L^{2}+3E_{s} r^{2}} \right) \left( {h+LS_{t}} \right) \left( {3C_{t}^2 E_{s} r^{2}L+C_{t}^2 L_{v}^2 LG_{s} k_{s} +L^{2}G_{s} k_{s} L_{v} +3E_{s} r^{2}L_v } \right) }; \\ E_{99}&= \frac{3}{2}\frac{E_s \pi r^{4}G_s k_s C_t \left( {3L^{2}G_{s} k_{s} L_{v} +9E_{s} r^{2}L_{v }+3C_t^2 E_{s} r^{2}L+C_t^2 L_{v}^2 LG_{s} k_{s} } \right) }{L_{v} \left( {G_{s} k_{s} L^{2}+3E_s r^{2}} \right) \left( {h+LS_t } \right) \left( {3C_t^2 E_s r^{2}L+C_t^2 L_{v}^2 LG_{s} k_{s} +L^{2}G_{s} k_{s} L_{v} +3E_{s} r^{2}L_v } \right) }; \\ K_{11}&= -\frac{1}{4}\frac{\pi r^{4}C_t G_s \left( {\begin{array}{l} -2L_{v}^2 C_{t}^2 G_{s}^2 Lk_s -6E_{s} LhL_{v} C_{t}^2 G_{s} k_{s} -6C_{t}^2 LE_{s} r^{2}G_{s} -LE_s L_v^2 G_s k_s -3L_v E_s^2 Lhk_s \\ -3LE_s^2 r^{2}-6hE_s^2 r^{2}-2hL_v^2 E_s G_s k_s +LL_v^2 E_s C_t^2 G_s k_s +3LE_s^2 hC_t^2 L_v k_s +3LE_s^2 C_t^2 r^{2} \\ \end{array}} \right) }{L_v \left( {h+LS_t } \right) \left( {\begin{array}{l} 3C_t^2 hE_s^2 r^{2}+L_v^2 C_t^2 E_s hG_s k_s +LL_v^2 G_s^2 k_s +3L_v E_s LhG_s k_s +3LE_s r^{2}G_s \\ +2hL_v^2 G_s^2 k_s +6hE_s r^{2}G_s -2hL_v^2 G_s^2 C_t^2 k_s -6hC_t^2 E_s r^{2}G_s \\ \end{array}} \right) };\\ K_{12}&= K_{21} =-\frac{1}{4}\frac{\pi r^{4}C_t S_t G_s \left( {E_{s} -2G_{s} } \right) \left( {3E_{s} r^{2}+L_{v}^2 G_{s} k_{s} +3hL_{v} E_{s} k_{s} } \right) }{L_{v} \left( {\begin{array}{l} 3C_{t}^2 hE_{s}^2 r^{2}+L_{v}^2 C_{t}^2 E_{s} hG_{s} k_{s} +LL_v^2 G_s^2 k_{s} +3L_{v} E_{s} LhG_{s} k_{s} +3LE_{s} r^{2}G_{s} \\ +2hL_{v}^2 G_{s}^2 k_{s} +6hE_{s} r^{2}G_{s} -2hL_{v}^2 G_{s}^2 C_t^2 k_s -6hC_t^2 E_s r^{2}G_s \\ \end{array}} \right) };\\ K_{22}&= \frac{1}{4}\frac{\pi r^{4}G_s \left( {h+LS_t } \right) \left( {2G_s -2C_t^2 G_s +C_t^2 E_s } \right) \left( {3E_{s} r^{2}+L_{v}^2 G_{s} k_{s} +3hE_{s} k_{s} L_{v} } \right) }{LL_{v} C_{t} \left( {\begin{array}{l} 3C_{t}^2 hE_{s}^2 r^{2}+L_{v}^2 C_{t}^2 E_{s} hG_{s} k_{s} +LL_{v}^2 G_s^2 k_{s} +3L_{v} E_{s} LhG_{s} k_{s} +3LE_{s} r^{2}G_{s} \\ +2hL_{v}^2 G_{s}^2 k_{s} +6hE_{s} r^{2}G_{s} -2hL_{v}^2 G_{s}^2 C_{t}^2 k_s -6hC_{t}^2 E_{s} r^{2}G_{s} \\ \end{array}} \right) };\\ K_{13}&= K_{31} =K_{23} =K_{32} =0;K_{33} = \frac{1}{2}\frac{G_{s} \pi r^{4}}{LC_{t} \left( {h+LS_{t} } \right) };\\ K_{44}&= \frac{1}{4}\frac{\pi r^{4}C_{t} E_{s} \left( { \begin{array}{l} 3LE_{s}^2 C_{t}^2 r^{2}+LL_{v}^2 E_{s} C_{t}^2 G_{s} k_{s} +6E_{s} hLC_{t}^2 L_{v} G_{s} k_{s} +4hL_{v}^2 G_{s}^2 k_{s} +6LE_{s} r^{2}G_{s} +2LL_{v}^2 G_{s}^2 k_{s} \\ +12hE_{s} r^{2}G_s +12hLL_v G_{s}^2 k_{s} -6C_{t}^2 LE_{s} r^{2}G _s -2L_{v}^2 C_{t}^2 G_s^2 Lk_{s} -12LG_{s}^2 hC_{t}^2 L_{v} k_{s} \\ \end{array}} \right) }{L_v \left( {h+LS_t } \right) \left( {\begin{array}{l} 4hL_{v}^2 G_{s}^2 C_{t}^2 k_{s} +12hC_{t}^2 E_{s} r^{2}G_{s} +6LE_{s} hL_{v} G_s k_{s} +3LE_{s}^2 r^{2}+6hE_s^2 r^{2} \\ +2hL_{v}^2 E_{s} G_s k_{s} +LE_{s} L_v^2 G_{s} k_{s} -6C_{t}^2 E_{s}^2 hr^{2}-2L_{v}^2 C_t^2 E_{s} hG_{s} k_{s} \\ \end{array}} \right) };\\ K_{45}&= K_{54} =-\frac{1}{4}\frac{\pi r^{4}C_t S_t E_s \left( {E_{s} -2G_{s} } \right) \left( {6hL_{v} G_{s} k_{s} +3E_{s} r^{2}+L_{v}^2 G_{s} k_{s} } \right) }{L_v \left( {\begin{array}{l} 4hL_{v}^2 G_{s}^2 C_{t}^2 k_{s} +12hC_{t}^2 E_{s} r^{2}G_{s} +6LE_{s} hL_{v} G_{s} k_{s} +3LE_{s}^2 r^{2}+6hE_{s}^2 {r}^{2} \\ +2hL_{v}^2 E_{s} G_{s} k_{s} +LE_{s} L_{v}^2 G_{s} k_{s} -6C_{t}^2 E_{s}^2 hr^ {2}-2L_{v}^2 C_{t}^2 E_{s} hG_{s} k_{s} \\ \end{array}} \right) };\\ K_{55}&= -\frac{1}{4}\frac{\pi r^{4}E_{s} \left( {h+LS_t } \right) \left( {C_{t}^2 E_{s} -E_{s} -2C_{t}^2 G_{s} } \right) \left( {6hL_{v} G_{s} k_{s} +3E_{s}^2 r^{2}+L_{v}^2 G_{s} k_{s} } \right) }{LL_{v} C_{t} \left( {\begin{array}{l} 4hL_{v}^2 G_{s}^2 C_{t}^2 k_s +12hC_{t}^2 E_s {r}^{2}G_s +6LE_{s} hL_{v} G_{s} k_{s} +3LE_{s}^2 r^{2}+6hE_{s}^2 r^{2} \\ +2hL_{v}^2 E_{s} G_{s} k_{s} +LE_{s} L_{v}^2 G_{s} k_{s} -6C_{t}^2 E_{s}^2 hr^{2}-2L_{v}^2 C_{t}^2 E_{s} hG_{s} k_{s} \\ \end{array}} \right) };\\ K_{66}&= \frac{1}{4}\frac{\pi r^{4}E_s \left( {h+LS_t } \right) }{LL_{v} C_{t} \left( {L+2h} \right) };K_{67} =K_{76} =0;K_{77} =\frac{1}{4}\frac{\pi r^{4}E_{s} }{LC_{t} \left( {h+LS_{t} } \right) };\\ K_{88}&= \frac{1}{4}\frac{\pi r^{4}E_{s} }{LC_{t} \left( {h+LS_{t} } \right) };K_{89} =K_{98} =0;K_{99} =\frac{1}{4} \frac{\pi r^{4}C_{t} E_{s} }{L_{v} \left( {h+LS_{t} } \right) }. \\ \end{aligned}$$