Dielectrophoretic cell motion model over periodic microelectrodes with unit-cell approach

Abstract

The micro-separator constructed with periodic bottom microelectrodes and a continuous top electrode has been developed previously for continuous cell sorting by dielectrophoresis. To understand its full potential and to facilitate future device development, the working mechanism of such electrode design is investigated by mathematical simulation. We first present a unit-cell methodology to model spatial electric field strength (E) over the microelectrode space due to its periodic nature. Unit-cell methodology is useful in modeling of E distribution for the microelectrode space, allowing computing spatial dielectrophoretic force with much less computational efforts. By using the computed dielectrophoretic force, a cell motion model, which takes into consideration the dielectrophoretic, Stokes, buoyancy and gravitational forces on a cell, is established for the prediction of cell trajectory over the separation channel. This study demonstrates the validity of this model in predicting live and dead NIH-3T3 cells motions over the microelectrode space of the micro-separator by comparing numerical and experimental results. In conclusion, a mathematical model that combines unit-cell methodology and cell motion model has been proposed and has demonstrated its potential use as an effective tool for the evaluation of electrode with a periodic nature.

Appendices

Appendix 1: Model for E simulation

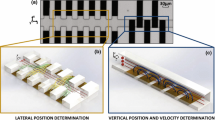
The theoretical model, as shown in Fig. 2a, has dimensions of 1,104.7 µm × 1,003.4 µm × 32 µm (length, L × width, W × height, H). It is constructed with a continuous top electrode and an array of 9 × 9 discrete bottom microelectrodes. The microelectrodes are modeled with dimensions and arrangement as shown in Fig. 1c, and at 1.2 µm below the model bottom surface to match the actual design. The setting of 200 µm for the spacing between the closest microelectrode and the respective sidewall (l) is to minimize boundary effect caused by the sidewalls.

Applying quasi-electrostatic approximation, the distribution of E ($= - \nabla \Phi$, where $\Phi$ is the electrical potential) for the model domain could be obtained by solving the Laplace’s equation $\left( {\nabla \cdot \nabla\Phi = 0} \right)$. With voltage drop over the top and bottom ITO conductors (under experimental conditions at f = 250 kHz and σ _f = 503.4 µS/cm), the effective voltage across the DEP buffer in the microchannel (∆V _Channel ) over the electrode space was computed to be 62.0 % V _SEP (simulation results not shown). Hence, with V _SEP of 2.5 and 3.5 V_P in the experiments, the corresponding ∆V _Channel was 1.55 and 2.17 V_P, respectively. With these considerations, the boundary conditions to the model are as follows:

• $\Phi =\Delta \varvec{V}_{{\varvec{Channel}}}$ to all triangular red filled areas on the model bottom surface with each area representing a single discrete microelectrode.

• $\Phi = 0$ to the model top surface representing the continuous top electrode.

• $\nabla \cdot\Phi = 0$ to all other surfaces representing the insulating boundaries. These surfaces include the 1.2-µm-thick edge surfaces of microelectrodes, the bottom surface of the model and the sidewalls.

To assess the grid independency of the E solutions, the model was meshed under: (1) a coarse mesh with ~3.527 × 10⁷ elements and (2) a fine mesh with ~5.555 × 10⁷ elements. With the maximum differences in E between the two meshed cases less than 3.06 % for all z-elevations studied, the accuracy presented by the coarse mesh is therefore acceptable.

Appendix 2: Unit-cell domains

Figure 6 presents the six unit-cell domains. The geometries, dimensions and locations for each unit-cell domain defined in the theoretical model are described as follows:

Fig. 6

Geometries, dimensions and locations for six different unit-cell domains defined in theoretical model

• Unit-cell A, as shown in Fig. 6a, has its domain corner at (x, y, z) = (0 µm, 544.7 µm, 0 µm) with dimensions of 432.5 µm × 400 µm × 32 µm (L × W × H). Its domain includes the space with the upper left 3 × 3 microelectrodes of the 9 × 9 microelectrodes.

• Unit-cell B, as shown in Fig. 6b, has its domain corner at (x, y, z) = (0 µm, 487.7 µm, 0 µm) with dimensions of 432.5 µm × 60 µm × 32 µm (L × W × H). Its domain includes the space with the 1 × 3 microelectrodes on the 4th row across from the 1st to the 3rd columns of the 9 × 9 microelectrodes.

• Unit-cell C, as shown in Fig. 6c, has its domain corner at (x, y, z) = (432.5 µm, 580.7 µm, 0 µm) with dimensions of 80 µm × 400 µm × 32 µm (L × W × H). Its domain includes the space with the 3 × 1 microelectrodes on the 4th column across from the 1st to the 3rd rows of the 9 × 9 microelectrodes.

• Unit-cell D, as shown in Fig. 6d, has its domain corner at (x, y, z) = (432.5 µm, 520.7 µm, 0 µm) with dimensions of 80 µm × 60 µm × 32 µm (L × W × H). Its domain includes the space with the single microelectrode on the 4th row and the 4th column of the 9 × 9 microelectrodes.

• Unit-cell E, as shown in Fig. 6e, has its domain corner at (x, y, z) = (672.5 µm, 613.7 µm, 0 µm) with dimensions of 430 µm × 380 µm × 32 µm (L × W × H). Its domain includes the space with the upper right 3 × 3 microelectrodes of the 9 × 9 microelectrodes.

• Unit-cell F, as shown in Fig. 6f, has its domain corner at (x, y, z) = (672.5 µm, 553.7 µm, 0 µm) with dimensions of 430 µm × 60 µm × 32 µm (L × W × H). Its domain includes the space with the 1 × 3 microelectrodes on the 4th row across from the 7th to the 9th columns of the 9 × 9 microelectrodes.

Appendix 3: Analysis on t _z and t _x

The approach to estimate t _z and t _x is as follows:

• (a) For a cell at the assumed z-elevation (z _i ) within the space in a unit-cell D (i.e., a repeating unit-cell of the theoretical model), the $\overline{{\left\langle {{\varvec{F}}_{{{\mathbf{DEP\_}}\varvec{z}}} } \right\rangle }} |_{{z_{i} }}$ on the cell is first calculated. $\overline{{\left\langle {{\varvec{F}}_{{{\mathbf{DEP\_}}\varvec{z}}} } \right\rangle }} |_{{z_{i} }}$ denotes the averaged z-directional dielectrophoretic force over the x–y plane of the unit-cell D at z _i and is expressed as:

  $$\overline{{\left\langle {{\varvec{F}}_{{{\mathbf{DEP\_}}\varvec{z}}} } \right\rangle }} |_{{z_{i} }} = \pi \varepsilon_{\text{f}} R^{3} \text{Re} \left[ {f_{{\text{cm}}} } \right]\left( {\overline{{\frac{\partial }{\partial z}\left| \varvec{E} \right|^{2} }} |_{{z_{i} }} } \right),\quad \text{where}\quad \overline{{\;\frac{\partial }{\partial z}\left| \varvec{E} \right|^{2} }} |_{{z_{i} }} = \frac{{\sum\nolimits_{x = i}^{m} {\sum\nolimits_{y = j}^{n} {\left( {\frac{\partial }{\partial z}\left| \varvec{E} \right|^{2} } \right)_{{x,y,z_{i} }} } } }}{{m{ \times }n}}$$

  (11)

• (b) The averaged z-directional velocity at z _i for the cell $\left( {\overline{{w_{\text{c}} }} |_{{z_{i} }} } \right)$ is then calculated by dividing the resultant z-component force on the cell by the F _Stokes coefficient $\left( {f = 6\pi \eta RK_{z} } \right)$:

  $$\overline{{w_{\text{c}} }} |_{{z_{i} }} = \left( {\frac{{\left( {\rho_{\text{f}} - \rho_{\text{c}} } \right)\text{V}_{\text{c}} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {g} + \overline{{\left\langle {{\varvec{F}}_{{{\mathbf{DEP\_}}\varvec{z}}} } \right\rangle }} |_{{z_{i} }} }}{{6\pi \eta RK_{z} |_{{z_{i} }} }}} \right)$$

  (12)

  where $K_{z} |_{{z_{i} }}$ is the F _Stokes correction factor for the cell levitated at z _i .

• (c) The required time (t _j ) for a cell experiencing an averaged positive z-component force to ascend from a lower z-elevation z _l to a higher z-elevation (z _h ) or a cell experiencing an averaged negative z-component force to descend from z _h to z _l can be estimated as:

  $$\begin{aligned} t_{j} & = \left| {\frac{{z_{l} - z_{h} }}{{\overline{{w_{\text{c}} }} |_{{z_{l} }} }}} \right|\,\text{for cell experiencing an averaged positive}\, z \text{-component force} \\ & = \left| {\frac{{z_{h} - z_{l} }}{{\overline{{w_{\text{c}} }} |_{{z_{h} }} }}} \right|\,\text{for cell experiencing an averaged negative}\, z \text{-component force} \\ \end{aligned} $$

  (13)

• (d) The time (t _z ) taken for the cell experiences an averaged positive/negative z-component force to travel from the lowest/highest possible z-elevation to the highest/lowest possible z-elevation (i.e., assuming a minimum gap of 1.1R between the cell center and microchannel top/bottom surface) is estimated as:

  $$t_{z} = \sum\limits_{{}}^{{}} {t_{j} }$$

  (14)

• (e) The time for cell of a similar type to traverse over 100 columns of microelectrode array (t _x ) is estimated by taking the average time for twelve cells of a similar type traversing the first 32 microelectrode columns in the experimental images and multiples by $\frac{100}{32}$. From experimental images on the separation of live/dead NIH-3T3 cells, t _x for live and dead cells, respectively, were 9.27 and 5.10 s under V _SEP of 2.5 V_P, and 14.01 and 5.00 s, respectively, under V _SEP of 3.5 V_P.

• (f) By comparing $\frac{{t_{z} }}{{t_{x} }}$, the timescale for a cell in descent or ascent with respect to that in traversing over the microelectrode array can be obtained. If $\frac{{t_{z} }}{{t_{x} }} \to 0\,\%$, the cell is considered to settle instantaneously upon entering the microelectrode region and traverses the microelectrode array at the settled z-elevation (z _s). If $\frac{{t_{z} }}{{t_{x} }}$ is large, the cell settles gradually and only reaches the presumed z _s after it traverses a substantial number of microelectrode columns (or may not even settle at the presumed z _s even it has traversed the entire microelectrode array if $\frac{{t_{z} }}{{t_{x} }} \ge 100\%$). In such scenario, the cell traverses microelectrode array with changing z-elevation.

Figure 7 presents t _z for live and dead cells that descend from z _i of 1.1R below the microchannel top surface to z _i of 1.1R above the microchannel bottom surface, under ∆V _Channel of: (a) 1.55 V_P, and (b) 2.17 V_P. The descent for live cell is rapid, with t _z of 0.637 and 1.098 s for 2.17 V_P and 1.55 V_P, respectively. A smaller t _z at increased ∆V _Channel is attributed to a stronger positive $\overline{{\left\langle {{\varvec{F}}_{{{\mathbf{DEP\_}}\varvec{z}}} } \right\rangle }} |_{{z_{i} }}$ on the live cell. For dead cell with neutral DEP behavior, its descent is much more gradual than that of the live cell, with t _z of 7.301 s under 1.55 V_P and 7.483 s under 2.17 V_P.

Fig. 7

t _z for live cell (that has nominal diameter of Ø17.34-µm) to descend from z _i of 22.463 to 9.537 µm and for dead cell (that has nominal diameter of Ø16.73-µm) to descend from 22.7895 to 9.2015 µm in 32.0-µm-height microchannel under ∆V _Channel of: a 1.55 V_P, and b 2.17 V_P

With the highest and lowest ∆V _Channel applied, $\frac{{t_{z} }}{{t_{x} }}$ for live cells were only 4.55 and 11.84 %, respectively. This implies that live cells traverse most of the microelectrode array with z-elevations near to the microchannel bottom surface. With $\frac{{t_{z} }}{{t_{x} }} \ge 143.16\,\%$ for dead cells, this signifies that dead cells would traverse the microelectrode array at many possible z-elevations, with its z-elevation strongly depends on its initial z-elevation.