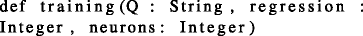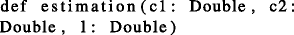Scalable aggregation predictive analytics

Abstract

We introduce a predictive modeling solution that provides high quality predictive analytics over aggregation queries in Big Data environments. Our predictive methodology is generally applicable in environments in which large-scale data owners may or may not restrict access to their data and allow only aggregation operators like COUNT to be executed over their data. In this context, our methodology is based on historical queries and their answers to accurately predict ad-hoc queries’ answers. We focus on the widely used set-cardinality, i.e., COUNT, aggregation query, as COUNT is a fundamental operator for both internal data system optimizations and for aggregation-oriented data exploration and predictive analytics. We contribute a novel, query-driven Machine Learning (ML) model whose goals are to: (i) learn the query-answer space from past issued queries, (ii) associate the query space with local linear regression & associative function estimators, (iii) define query similarity, and (iv) predict the cardinality of the answer set of unseen incoming queries, referred to the Set Cardinality Prediction (SCP) problem. Our ML model incorporates incremental ML algorithms for ensuring high quality prediction results. The significance of contribution lies in that it (i) is the only query-driven solution applicable over general Big Data environments, which include restricted-access data, (ii) offers incremental learning adjusted for arriving ad-hoc queries, which is well suited for query-driven data exploration, and (iii) offers a performance (in terms of scalability, SCP accuracy, processing time, and memory requirements) that is superior to data-centric approaches. We provide a comprehensive performance evaluation of our model evaluating its sensitivity, scalability and efficiency for quality predictive analytics. In addition, we report on the development and incorporation of our ML model in Spark showing its superior performance compared to the Spark’s COUNT method.

1 Introduction

Recent R&D efforts in the modern big data era have been dominated by efforts to accommodate distributed big datasets with frameworks that enable highly quality and scalable distributed/parallel data analyzes. Platforms such as MapReduce [14], Yarn [29], Spark [32] and Mahout [22] are nowadays commonplace. Predictive modeling [26], [23] and exploratory analysis [2, 3, 6, 20] are commonly based on statistical aggregation operators over the results of exploration queries [4, 7]. Such queries involve large datasets (which may themselves be the result of linking of other different datasets) and a number of range predicates over multidimensional data vectorial representation, structured, semi- and unstructured data. High quality query-driven data exploration and quality modeling is becoming increasingly important in the presence of large-scale data since accurately predicting aggregations over range predicate queries is a fundamental data exploration task [12] in big data systems. Frequently, data analysts, data scientists, and statisticians are in search of approximate answers to such queries over unknown data subspaces, which supports knowledge discovery and underlying data function estimation. Imagine exploratory and predictive analytics [9] based on a stream of such aggregation operators over data subspaces being issued, until the scientists/analysts extract sufficient statistics or fit local function estimators, e.g., coefficient of determination, product-moment correlation coefficient, and multivariate local linear approximation over the subspaces of interest.

In modern big data systems like Spark [32], often data to be analyzed possibly extends over a large number of federated data nodes, perhaps even crossing different administration domains and/or where data owners (nodes) may only permit restricted accesses (e.g., aggregations) over their data. Similarly, in the modern big data era, large datasets are often stored in the Cloud. Hence, even when access is not restricted, accesses to raw data needed to answer aggregate queries are costly money-wise. Quality predictive modeling solutions which are widely applicable, even in such scenarios, are highly desirable.

Consider a d-dimensional data space $\mathbf {x} \in \mathbb {R}^{d}$.

Definition 1 (Range Query)

Let a d-dim. box be defined by two boundary vectors [a ₁,…,a _d ]^⊤ and [b ₁,…,b _d ]^⊤, a _i ≤ b _i , $a_{i},b_{i} \in \mathbb {R}$. A range query is represented by the 2d-dimensional vector q = [a ₁, b ₁, a ₂, b ₂,…,a _d , b _d ]^⊤ where a _i and b _i is lower and higher value, respectively, for the i-th dimension. Query q is a hyper-rectangle with faces parallel to the axes.

Definition 2 (Query Distance)

¹ The normalized Euclidean distance between queries q and q ^′ is $\lVert \mathbf {q} - \mathbf {q^{\prime }} \rVert _{2} = \frac {1}{\sqrt {2d}}{\sum }_{i = 1}^{d}\left (a_{i}-a^{\prime }_{i}\right )^{2} + \left (b_{i}-b^{\prime }_{i}\right )^{2}$, where $\frac {1}{\sqrt {2d}}$ is a normalization factor since $0 \leq \lVert \mathbf {q} - \mathbf {q}^{\prime } \rVert _{2} \leq \sqrt {2d}$.

Definition 3 (Answer Set Cardinality)

Given a range query q and a dataset $\mathcal {B}$ of data points $\mathbf {x} \in \mathbb {R}^{d}$, $y \in \mathbb {N}$ is the cardinality of the answer set of those $\mathbf {x} \in \mathcal {B}$ in the interior of the hyper-rectangle defined by query q satisfying a _i ≤ x _i ≤ b _i , ∀i.

The reader could refer to Appendix for a nomenclature.

The reason we focus on the COUNT aggregation operator is that the answer Set Cardinality Prediction (SCP) of a multidimensional range query is a fundamental task, playing a central role in predictive modeling. With multidimensional range queries, analysts define the subspaces in $\mathbb {R}^{d}$ of interest within the overall data space. High quality cardinality prediction in such subspaces then becomes important for data mining, data exploration, time series analysis, and big data visualization tasks [9, 12] of data (sub)spaces of interest.

In predictive modeling, data scientists routinely define specific regions of a large dataset that are worth exploring and wish to derive and accurately predict statistics over the populations of these regions. This amounts to the SCP of the corresponding range queries. In addition to being an important aggregation operator, in database systems accurate cardinality prediction (which amounts to the well known selectivity estimation problem) is explicitly used for query processing optimization, empowering query optimizers to choose, for instance, the access plan which produces the smallest intermediate-query results (which have to be retrieved from disks and communicated over the network) saving time, resource waste, and money (e.g., in Clouds). Furthermore, SCP is a core operator in modern big data frameworks. Notably, in Spark [32] one of the five fundamental actions defined is the so-called count action, which is executed over the underlying raw data at each data node.

1.1 Motivation & research objectives

Well-established and widely adopted techniques for Approximate aggregation-Query Processing (AQP) based on sampling, histograms, self-tuning histograms, wavelets, and sketches [13] have been proposed. Their fundamental and naturally acceptable assumption is that the underlying data are always accessible and available, thus it is feasible to create and maintain their statistical structures. For instance, histograms [15] require scanning of all data to be constructed and being up-to-date; the self-tuning histograms [1] require additionally the execution of queries to fine tune their statistical structures; the sampling methods [16] execute the queries over the sample to extrapolate the cardinality prediction result.

Consider now a big data environment, where a federation of data nodes store large datasets. There are cases where the data access to these nodes’ data may be either restricted, (e.g., government medical and DNA databases and demographic and neighborhood statistic datasets). Furthermore, many real-world large-scale data systems may limit the number of queries that can be issued and/or charge for excessive data accesses. For example, there may exist per-IP limits (for web interface queries) or per developer key limits (for API based queries). Even when the (daily) limit is high enough, repeated executions actually have high monetary cost (e.g., in cloud deployments), waste communication overhead due to remote query execution, and computational resources. The accessed data nodes can either fully execute the queries (to produce exact results) or locally deploy an AQP technique to produce estimates. In the latter case, we must rely upon the SCP accuracy provided by the applied traditional AQP technique. Hence, the cardinality prediction accuracy is upper bounded by the predictability capability of the AQP method.

The above discussion raises the following desiderata: it is important to develop quality AQP techniques that:

• D1: are applicable to all data-environment scenarios (restricted-access or not),

• D2: are inexpensive, i.e., avoid relying on excessive querying of and communication with the data nodes, while

• D3: offering high prediction accuracy, and

• D4: being prudent in terms of compute-network-store resource utilization.

Let us consider an indicative baseline solution for AQP in our environment. One approach is to store, e.g., locally to a central node, all the AQP structures (e.g., histograms, samples, sketches, etc.) from a federation of data nodes. Thus, we can simply locally access this node for SCP. Firstly, this violates our first desideratum, as privacy issues emerge (data access restrictions). Obviously, retaining all AQP structures, provides one with the whole valuable information about the underlying data (e.g., in the case of histograms, we obtain the underlying probability data distribution p(x), while in sampling methods we retain actual samples from the remote datasets). Even, in cases where the local accesses to AQP structures were secured (which is again subject to major security concerns), we would have to cope with the problem of AQP structure updates. The maintenance of those structures in the face of updates demands high network bandwidth overhead, cost for data transfer (in a Cloud setting), latency for communicating with the remote nodes during updates of the underlying dataset at these nodes, and scalability and performance bottleneck problems arise at the central node. Therefore, this approach does not scale well and can be expensive, violating our 2nd and 3rd criteria above.

An alternative baseline solution would be to do away with the central node and send the query to the data nodes, which maintain traditional AQP statistical structure(s) and send back their results to the querying node. As before, this violates many of our desiderata. It is not applicable to restricted-access scenarios (violating criterion 1) and involves heavy querying of the data node (violating criteria 2 and 4). Even if this was the case (by violating criteria 1, 2, and 4), the construction and maintenance of an AQP structure would become a prohibited solution; we struggle with huge volumes of data (data universe explosion phenomenon; imagine only the creation of a multidimensional histogram over 1 zettabyte). These facts help expose the formidable challenges to the problem at hand, (a significant problem for large-scale predictive analytics) which to the best of our knowledge, has not been studied before. In this work we study a query-driven SCP in a big data system taking into consideration the above-mentioned desiderata. Although significant data-centric AQP approaches for cardinality prediction have been proposed [13] a solution for our intended environments of use is currently not available.

There are three fundamental pressures at play here. The first pertains to the development of a solution for cardinality prediction that is efficient, and scalable, especially for distributed scale-out environments, wherein extra communication costs, remote invocation techniques, and estimation latency are introduced. The second pertains to the quality of cardinality prediction results in terms of accuracy and model fitting, where as we shall see traditional solutions fall short. The third concerns the wide-applicability of a proposed method, taking into account environments where data accesses may be restricted, We propose a solution that addresses all these tensions. Conceptually, its fundamental difference from related works is that it is query-driven, as opposed to data-driven, and is thus based on a ML model (trained by a number of queries sent to a data node) and later utilized to predict answers to new incoming queries.

The challenging aim of our approach is to swiftly provide cardinality prediction of ad-hoc, unseen queries while (i) avoiding executing them over a data node, saving communication and computational resources and money, and (ii) not relying on any knowledge on the p(x), and any knowledge about nodes’ data. Through our query-driven SCP, an inquisitive data scientist, who explores data spaces, issues aggregate queries, and discovers hidden data insights, can extract accurate knowledge, efficiently and inexpensively.

1.2 Related work

Given a d-dim. data space $\mathbf {x} \in \mathbb {R}^{d}$ the holy grail approaches focus on: (i) inspecting the (possibly huge) underlying dataset and estimate the underlying probability density function (pdf) p(x). Histograms (typically multidimensional) as fundamental data summarization techniques are the cornerstone, whereby the estimation of p(x) is highly exploited for SCP of range queries, e.g., [1, 15]. The traditional methods of building histograms do not scale well with big datasets. Histograms need to be periodically rebuilt in order to update p(x) thus, exacerbating the overhead of this approach. Central to our thinking is the observation that a histogram is constructed solely from data, thus obviously being not applicable to our problem for the above-mentioned reasons. Histograms are also inherently unaware on the cardinality prediction requests, i.e., query patterns. Their construction method rely neither on query distribution p(q) nor on joint p(q, y) but only on p(x). As a result, such methods do not yield the most appropriate histogram for a given p(q) [11]. The limitations of this method are also well-known [27, 30].

To partially address some of the above limitations, prior work has proposed self-tuning histograms (STHs) e.g., [1, 27]. The STHs learn a centrally stored dataset from scratch (i.e., starting with no buckets) and rely only on the cardinality result provided by the execution of a query, referred to as Query Feedback Records (QFR). STHs exploit the actual cardinality from QFR and use this information to build and refine traditional histograms. Formally, given a query q over data with cardinality y, the methods of STHs estimate the conditional p(x|y, q) since the main purpose is to construct and tune a histogram conditioned on query patterns. Fundamentally, the limitations in STHs in our problem stem from the fact that they estimate p(x|y, q), thus, having to data access (in multidimensional STHs, at least one scan of the set $\mathcal {B}$ is required), deal with the underlying data distribution and make certain assumptions of the statistical dependencies of data.

Other histogram-based cardinality prediction methods utilize wavelets [31] or entropy-based [28]; the list is not exhausted. Briefly, the idea is to apply wavelet decomposition to the dataset to obtain a compact data synopsis based on the wavelet coefficients. By nature, wavelets-based AQP relies on the synopsis construction over data thus could not be applied to our problem. Overall, STHs and the other advanced histogram-based approaches, are associated with data access for estimating p(x) or any other p(x|q,…) thus not applicable in our problem. Sampling methods [16] have been also proposed for SCP. They share the common idea to evaluate the query over a small subset of the dataset and extrapolate the observed cardinality. Finally, another approach for AQP answering to SCP is data sketching; we refer the reader to [13] for a useful survey of sketching techniques. Sketching algorithms construct estimators from the raw data and yielding a function of these estimators as the answer to the query. Therefore, as discussed above, we neither have access to data nor to a sample of them, thus yielding the data sketching and sampling methods inapplicable to our problem.

In conclusion, the data-centric approaches in related work are not applicable to our problem since they require explicit access to data to construct their AQP structures and maintain them up-to-date. For this reason, our proposed solution to this novel setting is query-driven.

Our model can be highly useful when it is very costly (in time, money, communication bandwidth) to execute aggregation operators over the results of complex range queries (including joins of datasets and arbitrary selection predicates), when data are stored at the cloud, or at federations of data stores, across different administration domains, etc. And, to our knowledge, it is the only approach that can address this problem setting. It is worth noting that this paper significantly extends our previous work presented in [5]. The interesting reader could refer to [5] to assess the performance of our solution with respect to traditional data-centeric (AQP) systems for cardinality prediction namely with multidimensional histograms, popular self-tuning histograms, and sampling methods. In [5], through comprehensive experiments we showed that the query-driven approach, which extracts knowledge from the issued queries and corresponding answers, provides higher cardinality prediction accuracy and performance, while being more widely applicable. Based on the scalability and efficiency of this approach, we further generalize our model in [5] and implement generalized ML algorithms within the most popular big data system, Spark. Specifically, the major differences of the proposed generic ML model discussed in this paper with that of our paper in [5] are:

• We propose a generalization of the ML model in [5] by introducing (i) associative local linear regression models for cardinality prediction and (ii) the concept of the coefficients lattice in self-organizing maps statistical learning algorithm;

• We provide the theoretical analysis and convergence of the learning algorithms of the generalized ML model (Theorems 2 and 4);

• We implement our ML model within the Spark system;

• We provide comprehensive experiments showing the quality of prediction of our ML model through a variety of evaluation metrics.

• We experiment with the scalability performance of our ML model compared with the Spark’s COUNT method for answer-set cardinality estimation.

1.3 Organization

The structure of the paper is as follows: Section 2 reports on the rationale of our approach and the research challenges for the SCP, while summarizes the contribution and our research outcome. In Section 3, we provide preliminaries for unsupervised & heteroassociative competitive statistical learning and the self-organizing maps along with the problem formulation for SCP. Section 4 provides the set cardinality learning methodology, the machine learning algorithms over the novel introduced lattice concepts and the fundamental convergence theorems of our neuron-based model. In Section 5 we provide an implementation of our model in the Spark system, while Section 6 reports on a comprehensive performance and comparative assessment with the build-in Spark COUNT over real large-scale datasets introducing different experimental scenarios. Finally, Section 7 concludes the paper with future research directions.

2 Challenges & overview

Our approach is query-driven. The first requirement (and challenge) of our approach is to incrementally learn the query patterns p(q) at any time, thus being able to (i) detect possible changes to user interests on issuing queries and (ii) reason about the similarity between query patterns. The second requirement (and challenge) is to learn the association q → y between a query q and its cardinality y, i.e., p(y|q), thus being able to predict the cardinality. The third requirement (and challenge) is to learn such association without relying on the underlying p(x) which in our case is totally unknown and inaccessible. The fourth requirement (and challenge) is to update p(q) and p(q, y) based on changes in query patterns and to data. Query distributions are known to be non-uniform, with specific portion of the data space being more popular. However, query patterns change with time, reflecting changes of users interests to exploring different sections of the datasets of nodes. Hence, we must swiftly adapt and learn on-the-fly the new query patterns, updating p(q, y) and p(q). Furthermore, updates on the underlying datasets of nodes can independently occur, altering p(x). We must also deal with such mutations, implying the need to maintain the current q → y association, subject to updates of the underlying data. We require a model to meet the above-mentioned requirements.

2.1 Overview of COUNT predictive learning

Consider a set $\mathcal {Q} = \{(\mathbf {q}_{i},y_{i})\}_{i = 1}^{n}$ of training pairs and a new query q with actual result y. Our major aim is to predict its result $\hat {y}$ using only $\mathcal {Q}$ without executing q. Let us discuss some baseline solutions:

A first idea is to keep all pairs (q _i , y _i ) and given q we find the most similar query q _j with respect to Euclidean distance and predict $\hat {y} = y_{j}$, with $(\mathbf {q}_{j},y_{j}) \in \mathcal {Q}$. We can also involve the k closest queries to q and average their cardinality values, i.e., k-nearest neighbors regression, as will be further analyzed later. The major problems here are: (i) we must store and search all previous pairs for each new query; $\mathcal {Q}$ can be huge. Deciding which pairs to discard is not a trivial task (a new pair might convey useful information while another new one might be a redundant / repeated query); (ii) when data change (updates on raw data), which impacts the query results, it is not trivial to determine which pairs from $\mathcal {Q}$ and how many to update. Even worse, all pairs may need updating; (iii) when query patterns change (new user interests), then there may be many pairs in $\mathcal {Q}$ that will not contribute to cardinality prediction (the new queries are actually far distant to the previous ones) or even negatively impact the final result.

To avoid such problems we extract knowledge from $\mathcal {Q}$ as to how query and cardinality depend on each other. We could cluster similar queries given the Euclidean distance, thus forming a much smaller set $\mathcal {L}$ of representative (prototype) queries w with $|\mathcal {L}| \ll |\mathcal {Q}|$. For instance, $\mathbf {w} \in \mathcal {L}$ can be the centroid of those queries from $\mathcal {Q}_{\mathbf {w}} \subset \mathcal {Q}$ with distances from w be the smallest among all other representatives. However, we are not just interested in clustering $\mathcal {Q}$. We should partition $\mathcal {Q}$ aiming at cardinality prediction. An approach could be to assign to each $\mathbf {w}_{i} \in \mathcal {L}$ a ‘representative’ cardinality value, e.g., the average cardinality of those queries that belong to $\mathcal {Q}_{\mathbf {w}_{i}}$. Once this assignment is achieved, we only keep $\mathcal {L}$ and discard $\mathcal {Q}$.

Nonetheless, our requirements include incremental learning of the query space in light of cardinality prediction. We require an adaptive clustering algorithm that incrementally, i.e., with only one pass of $\mathcal {Q}$, quantizes $\mathcal {Q}$ but also with respect to minimizing the prediction error. Also, the adoption of an on-line quantization algorithm, like on-line k-means is not directly applicable in our case as we don’t wish to simply quantize the query space; we explicitly require quantization of the query space in light of cardinality prediction. Moreover, on-line regression methods, e.g., incremental regression trees [17], on-line support vector regression [24], could not fulfill all requirements. This is because, we also deal with the fact that queries are continuously observed, conveying the way users are interested in data exploration. The capability of the model to adapt to such changes requires explicit information on accessing the very specific regions of the query patterns space; this is neither easily provided nor supported by incremental regression methods. Moreover, the problem here is not only to adapt to changes on the query patterns but to decide which and how representative(s) or regions of the query patterns space to update upon data and/or query updates.

2.2 Contribution & research outcome

We introduce a novel and scalable Machine Learning (ML) model $\mathcal {M}$ that incrementally extracts information about the q → y association by learning p(q) and, in parallel, p(y|q). Once trained, model $\mathcal {M}$ predicts the cardinality of an unseen query without requesting its execution. The major technical contributions are:

• a prediction error-driven, associative local regression model for predicting the aggregate results of range queries.

• theoretical analysis of convergence of our machine learning algorithms over large-scale squared and absolute loss minimization.

• implementation of our algorithms in the Spark system.

• comprehensive experimental results analyzing the performance of our model and showcasing its benefits vis-à-vis the data-centric Spark’s COUNT method for set-cardinality estimation.

3 Preliminaries & problem formulation

3.1 Preliminaries

We overview the essentials of our ML model, namely Unsupervised Competitive Learning (UCL) [21] and Heteroassociative Competitive Learning (HCL) [19].

3.1.1 Unsupervised competitive learning

UCL partitions a query pattern space $\mathbb {R}^{2d}$ characterized by an unknown p(q), $\mathbf {q} \in \mathbb {R}^{2d}$. A prototype or neuron w _j represents a local region of $\mathbb {R}^{2d}$. UCL distributes M neurons w ₁,…,w _M in $\mathbb {R}^{2d}$ to approximate p(q). A UCL model learns as w _j changes in response to random training patterns. Competition selects which w _j the training pattern q modifies. Neuron w _j wins if it is the closest (based on 2-norm distance ∥q −w _j ∥₂) of the M neurons to q. During the learning phase of UCL, patterns q are projected onto their winning neurons, which competitively and adaptively move around the space to form optimal partitions that minimize the quantity $\int \lVert \mathbf {q}-\mathbf {w}_{j} {\rVert _{2}^{2}} p(\mathbf {q})\mathrm {d}\mathbf {q}$ with winning neuron w _j : ∥w _j −q∥₂ = min _i ∥w _i −q∥₂. The neurons upon a t-th training pattern q are incrementally updated as follows:

$$\begin{array}{@{}rcl@{}} {\Delta} \mathbf{w}_{j} = \beta(t) \left( \mathbf{q} - \mathbf{w}_{j}\right) \text{ and } {\Delta} \mathbf{w}_{i} = \mathbf{0} \text{, if } i \neq j, \end{array} $$

(1)

where learning rate β(t) ∈ (0,1] slowly decreases with the update step.

3.1.2 Kohonen’s self-organizing maps

Kohonen’s self-organizing maps (SOM) [19] is an advanced variant of a UCL, in which w _j corresponds to the j-th position r _j = [r _j1, r _j2] of a 2-dim. square lattice/matrix $\mathcal {L}$ (we notate $\mathbf {w}_{j} \in \mathcal {L}$). In SOM, neurons that are topologically close in the lattice correspond to patterns that are also closein $\mathbb {R}^{2d}$. This way a topographic mapping is learned between query pattern and lattice space. This is achieved by adapting not only the winner neuron w _j of a pattern q but also its topographical neighbors w _i to some degree through a Kernel distance function h(i, j; t) over the positions r _i and r _j of neurons w _i and w _j in $\mathcal {L}$, respectively. Usually, h(i, j; t) is a Gaussian neighborhood function:

$$ h(i, j;t) = \exp \left( -\frac{\parallel \mathbf{r}_{i} - \mathbf{r}_{j} {\parallel^{2}_{2}}}{2\rho^{2}(t)} \right). $$

(2)

Parameter ρ(t) is the width of the neighborhood with initial value ρ ₀ defined as $\rho (t) = \rho _{0} \exp (-\frac {t}{T_{\rho }})$, where T _ρ is a constant. A small width value corresponds to narrow neighborhood. We obtain SOM through an incremental update rule that adapts all neurons that are topographically close to w _j :

$$ {\Delta} \mathbf{w}_{i} = \beta(t)h(i, j;t)\left( \mathbf{q} - \mathbf{w}_{i}\right), \forall i. $$

(3)

A good choice of β(t) improves significantly the convergence of SOM [19]; usually $\beta (t) = \frac {\beta (t-1)}{1+\beta (t-1)}$ with β(0) = 1. SOM yields a high quality vector quantization from all UCL variants because of producing a structured ordering of the pattern vectors, i.e., similar query patterns are projected to similar neurons, making it ideal for our purposes. Figure 1 shows a SOM structure with neuron and position vectors before and after an update. UCL/SOM does not learn any conditional or joint association between different pattern spaces. In our case, we desire also to estimate an association between $\mathbb {R}^{2d}$ and $\mathbb {N}$, i.e., estimate p(q, y) with $\mathbf {q} \in \mathbb {R}^{2d}, y \in \mathbb {N}$, HCL comes into play.

Fig. 1

a A Self-organizing Map with neuron vectors w _j and position coordinates vector r _j ; b The adaptation of the self-organizing map after the projection of a query vector q to its closest neuron w _j on the neurons lattice $\mathcal {L}$

3.1.3 Heteroassociative competitive learning

HCL estimates indirectly an unknown joint p(q, y), while directly estimates a function $f: \mathbb {R}^{2d} \rightarrow \mathbb {N}$ over random pairs (q, y). In statistical learning theory [21], HCL refers to a function estimation model $\mathcal {M}(f, \alpha )$ (or simply $\mathcal {M}$) with parameter α ∈ Λ (Λ is a parameter space defined later) for estimating f. The problem of learning $\mathcal {M}$ is that of choosing from a set of functions f(q, α), α ∈ Λ, the one which minimizes the risk function:

$$ \mathcal{J}(\alpha) = \int L(y, f(\mathbf{q}, \alpha)) \mathrm{d}p(\mathbf{q},y), $$

(4)

given random pairs (q, y) drawn according to p(q, y) = p(q)p(y|q) with loss or estimation error $L(y, \hat {y})$ between actual y and predicted $\hat {y} = f(\mathbf {q}, \alpha )$, e.g., $L(y,\hat {y}) = |y - \hat {y}|$. The goal for HCL is to learn $\mathcal {M}(f, \alpha _{0})$ which minimizes $\mathcal {J}(\alpha )$ subject to unknown p(q, y), i.e., $\alpha _{0} = \arg \min _{\alpha \in {\Lambda }} \mathcal {J}(\alpha )$.

3.1.4 Stochastic gradient descent

Stochastic gradient descent (SGD) is considered to be one of the best methods for large scale loss minimization and has been experimentally and theoretically analyzed by [10]. Upon the presence of a t-th pattern (q, y), α(t) is updated by:

$$ {\Delta} \alpha(t) = - \beta(t) \nabla L(y,\hat{y};\alpha(t)), $$

(5)

where ∇L is the gradient of L at t-th pattern w.r.t. α(t).

3.2 Problem formulation

Consider a model $\mathcal {M}$ that estimates the cardinality prediction function

$$f: \mathbb{R}^{2d} \to \mathbb{N} $$

given a finite set $\mathcal {Q}$ of training pairs (q, y) drawn from the unknown p(q, y), i.e., y = f(q). The model $\mathcal {M}$ learns the mapping from query pattern space to cardinality domain by minimizing the risk function $\mathcal {J}(\alpha )$ in (4) with respect to a loss function (prediction error) $L(y,\hat {y})$. A loss function can be, e.g., λ-insensitive $L(y,\hat {y}) = \max \{|y-\hat {y}|-\lambda ,0\}, \lambda >0$, 0–1 loss $L(y,\hat {y}) = I(y \neq \hat {y})$ with I be the indicator function, squared loss $(y-\hat {y})^{2}$,or absolute $|y-\hat {y}|$.

The fundamental problem of the ML model for cardinality prediction is:

Problem 1

Given a dataset $\mathcal {B}$ and training pairs of queries and their answer-set cardinality values $(\mathbf {q}, y) \in \mathcal {Q}$, incrementally train a model $\mathcal {M}$ which minimizes $\mathcal {J}(\alpha )$.

4 Set cardinality predictive learning

4.1 Machine learning methodology

A natural, baseline solution for cardinality prediction is distance nearest-neighbors regression. This prediction scheme is based on utilizing the set cardinality values of similar historical queries to predict the set cardinality value for a new, unseen query. The notion of neighborhood is materialized by the distance (in some metric space, e.g., Euclidean space) of the unseen query q to a (stored) query $\mathbf {q}_{i} \in \mathcal {Q}$, whose cardinality value is y _i . Hence, the regression function for cardinality prediction y = f(q; k) refers to the average value of the cardinality values of the k-th closest stored queries q _i :

$$ y = f(\mathbf{q};k) = \frac{1}{|\mathcal{N}_{k}(\mathbf{q})|}\sum\limits_{i = 1}^{|\mathcal{N}_{k}(\mathbf{q})|}y_{i}: \mathbf{q}_{i} \in \mathcal{N}_{k}(\mathbf{q}), $$

(6)

where the neighborhood $\mathcal {N}_{k}(\mathbf {q})$ is the set of the k-th closest queries to unseen query q:

$$ \mathcal{N}_{k}(\mathbf{q}) = \{\mathbf{q}_{i} \in \mathcal{T}, \mathbf{q}^{\prime} \in \mathcal{T} \setminus \mathcal{N}_{k}(\mathbf{q}): \lVert \mathbf{q}_{i}-\mathbf{q}\rVert_{2} \leq \lVert \mathbf{q}^{\prime} - \mathbf{q} \rVert_{2}\}. $$

(7)

In this k-nearest neighbors regression (k-nn), the cardinality of the neighborhood k plays a significant impact on the accuracy of prediction. The choice of k is very critical: (i) a small value of k means that noise will have a higher influence on the prediction result; (ii) a large value of k, evidently, yields a computationally expensive prediction result and defeats the basic philosophy behind, i.e., queries that are near might have similar densities in cardinality values; e.g., by involving in the final prediction result irrelevant and non-similar queries. In general notion, k is chosen to be $\sqrt {|\mathcal {Q}|}$, where $|\mathcal {Q}|$ is the number of stored queries in $\mathcal {Q}$, thus, interdependent of the query dimensionality 2d. Moreover, a straightforward k-nn algorithm for cardinality prediction is $O(|\mathcal {Q}|d \log (k))$, which obviously, is not applicable for large-scale data-sets, especially when $k \sim \sqrt {|\mathcal {Q}|}$. This means that this (non-parametric) solution does not scale with the number of queries and dimensionality, thus, not suitable for scaling out for predictive analytics tasks like our problem.

We propose a solution, which scales with the number of queries and deals with the curse of dimensionality based on parametric regression, i.e., we attempt to incrementally extract knowledge from the $\mathcal {Q}$ set of historical queries and then, abstract a parametric model suitable to scale and, simultaneously, be computationally inexpensive for predictions. In this context, our scalable methodology learns from incoming queries and answers and dynamically builds a parametric model, thus (i) avoiding to maintain and process historical queries for making prediction and (ii) being capable to swiftly predict cardinality independent on the numbers of the queries.

Our objective is a scalable, parametric ML model $\mathcal {M}$ to:

• 1. incrementally quantize (cluster) the query pattern space, thus, abstracting the query space by certain M parameterized prototypes, with a user-specific fixed M;

• 2. learn the localities of the association q → y, thus, dealing with the curse of dimensionality [18] based on localized regression models;

• 3. predict the set cardinality given an unseen query in O(d log(M)) independent of the number of queries $|\mathcal {Q}|$.

The novelty of our model relies on the introduction of two simultaneous incremental learning tasks:

• Task 1: incremental query space quantization (UCL/SOM; unsupervised learning);

• Task 2: incremental local learning of the q → y association within the region of these neurons (HCL; supervised learning).

Both tasks rely on certain 2-dimensional lattices, where reside the parameters of the model. In Task 1, we abstract the lattice parameters as the query representatives (neurons). The parameters of the Task 2 refer to local output representatives (prototypes) depending on the representation of the prediction function, residing on a different lattice. In this work, we propose two variants for the cardinality prediction function f.

4.2 The lattice concept in machine learning methodology

4.2.1 Neuron input lattice

In this input lattice, hereinafter referred to as the neuron lattice $\mathcal {L}$, we estimate the parameters, i.e., SOM neurons, that represent the input space in our problem, i.e., the query patterns. The 2d-dimensional neurons $\mathbf {w}_{i} \in \mathcal {L}$ quantize the query space into a fixed number of M query sub-spaces. As will be elaborated later, this lattice is used for projecting an unseen query q onto a query sub-space and then leading to its associated output lattice for cardinality prediction.

4.2.2 Cardinality output lattice

In this output lattice, we estimate the (local) cardinality prototypes y _j , which are associated with each w _j . The y _j reside on a cardinality lattice $\mathcal {C}$ such that the j-th index of w _j refers to the j-th index of y _j . Hence, a point y _j in the cardinality lattice corresponds to a local associative constant function:

$$ f_{j}(\mathbf{q}) = y_{j}, \mathbf{q} \in \mathbb{R}^{2d}: j = \arg\min_{i \in [M]}\lVert \mathbf{q}-\mathbf{w}_{i} \rVert_{2}. $$

(8)

In the case of input lattice $\mathcal {L}$ and output lattice $\mathcal {C}$, the parameter set for model $\mathcal {M}$ is α = ({w _j },{y _j }),j = 1,…,M. Figure 2 shows the idea of the cardinality lattice.

Fig. 2

Cardinality lattice-based prediction: Projection- association-local prediction: Simultaneous UCL and HCL over lattices $\mathcal {L}$ and $\mathcal {C}$

4.2.3 Coefficient output lattice

In this output lattice, if the local associative function is varying considerably around a point, a piece-wise constant approximation may require many units. In this case, we refer to the estimation of the local linear regression coefficients $\mathbf {m}_{j} = [m_{j0}, m_{j1}, \ldots , m_{j2d}] \in \mathbb {R}^{2d + 1}$, which are associated with each query prototype w _j . That is the cardinality y is approximated by a linear combination of the query dimensions q = [q ₁,…,q _2d ], while m is the (2d + 1)-dimensional vector of the linear coefficients, with m ₀ being the intercept in the $\mathbb {R}^{2d} \times \mathbb {N}$ space. The m _j coefficients reside on a coefficient lattice $\mathcal {O}$ such that the j-th index of w _j refers to the j-th regression plane governed by the regression m _j q ^⊤. This defines a local regression plane over the query and cardinality space, defined by those queries that are projected on the query prototype w _j . Hence, a point m _j in the coefficient lattice corresponds to the parameter of the local linear regression function:

$$ f_{j}(\mathbf{q}) = \mathbf{m}_{j}\mathbf{q}^{\top}, \mathbf{q} \in \mathbb{R}^{2d}: j = \arg\min_{i \in [M]}\lVert \mathbf{q}-\mathbf{w}_{i} \rVert_{2}. $$

(9)

Figure 3 shows the idea of the coefficient lattice. In the case of input lattice $\mathcal {L}$ and output lattice $\mathcal {O}$, the parameter set for model $\mathcal {M}$ is α = ({w _j },{m _j }),j = 1,…,M.

Fig. 3

Coefficient lattice-based prediction: Projection- association-linear regression: Simultaneous UCL and HCL over lattices $\mathcal {L}$ and $\mathcal {O}$

4.3 Learning methodology

4.3.1 Overview

Consider the presence of a (random) training pair (q, y). The following steps demonstrate the methodology of exploiting such training pair for estimating the points on the: neuron, cardinality and regression lattices.

Projection

The query q from the training pair (q, y) is projected onto its (winner) closest neuron $\mathbf {w}_{j} \in \mathcal {L}$ from the neuron lattice. Certain neurons, including the winner w _j , are then adapted to this occurrence. In this step, we have to define the update rule Δw _i for the neurons in the neuron lattice.

Association

Simultaneously, the actual cardinality y from the training pair (q, y) is utilized to update certain points from the cardinality and regression lattices. Specifically, the corresponding prototype $y_{j} \in \mathcal {C}$, i.e., this is associated with the winner query neuron w _j , and the corresponding regression coefficient $\mathbf {m}_{j} \in \mathcal {O}$ are updated based on y and the query q (in the latter case) governed by feedback update rules. Such rules derive from the stochastic negative partial derivative (introduced later).

Prediction

The model $\mathcal {M}$ after locating the winner neuron w _j based on the input lattice, predicts the cardinality $\hat {y}$ using Kernel regression over (i) the local associative functions in the $\mathcal {C}$ lattice, and (ii) the local linear regression functions in the $\mathcal {O}$ lattice.

Feedback

The prediction result $\hat {y}$ feeds the $\mathcal {C}$ and $\mathcal {O}$ lattices for updating the cardinality prototypes and the regression coefficients, respectively.

4.4 The predictive learning algorithm

We adopt SOM for UCL since based on topology preservation we can claim that: if queries q and q ^′ are similar due to being projected onto the same neuron w _j of $\mathcal {L}$, then their images through the local associative and local regression functions f _j (q) and f _j (q ^′) on cardinality lattice $\mathcal {C}$ and coefficient lattice $\mathcal {O}$, respectively, are likely to be similar, too. This argument cannot be claimed by any other UCL method (e.g., k-means or fuzzy c-means clustering), which does not guarantee topological ordering of quantization vectors.

At this point, we can define the cardinality prediction function $\hat {y} = f(\mathbf {q},\alpha )$ based on the local associative and regression functions, and in the sequel, report on the loss function $L(y,\hat {y})$. Consider two range queries q, q ^′ normalized firstly in [0,1]^2d (only for simplicity in our analysis). Let the winner neuron $\mathbf {w}_{j} \in \mathcal {L}$ and its corresponding (i) local associative function f _j (q), i.e., cardinality prototype $y_{j} \in \mathcal {C}$ and (ii) local linear regression function f _j (q), i.e., regression coefficient $\mathbf {m}_{j} \in \mathcal {O}$ to a random query q.

The cardinality prediction f is not only based on f _j (q), but also on the contribution of the neighboring f _i (q) defined by the topographical neighborhood of winner w _j . This is achieved by a kernel function $\mathcal {K}_{\epsilon }(\lVert \mathbf {r}_{i} - \mathbf {r}_{j}\rVert _{2})$ over the normalized location vectors r _i and r _j (i.e., ∥r _i ∥,∥r _j ∥≤ 1) of the associated neurons w _i and w _j in the input lattice $\mathcal {L}$, respectively. That is, $\hat {y} = f(\mathbf {q},\alpha )$ is produced by the (Nadaraya-Watson) Kernel regression model:

$$ \hat{y} = f(\mathbf{q},\alpha) = \frac{{\sum}_{i = 1}^{M}\mathcal{K}_{\epsilon}(\lVert \mathbf{r}_{i} - \mathbf{r}_{j}\rVert)f_{i}(\mathbf{q})}{{\sum}_{i = 1}^{M}\mathcal{K}_{\epsilon}(\lVert \mathbf{r}_{i} - \mathbf{r}_{j}\rVert)} $$

(10)

with $j = \arg \min _{\mathbf {w}_{i} \in \mathcal {L}}\lVert \mathbf {q}-\mathbf {w}_{i}\rVert _{2}$. In this paper, we utilize the kernel $\mathcal {K}_{\epsilon }(x) = 0.75 \cdot \left (1- (\frac {x-0.5}{\epsilon })^{2}\right ) \cdot I(|x-\frac {1}{2}| \leq \epsilon )$, which is the Epanechnikov kernel function shifted to 0.5 and scaled by 0 < 𝜖 ≪ 0.5. Obviously, any other kernel functions can be also adopted e.g., uniform, triangular, quadratic, with Epanechnikov being most commonly used kernel for regression. Topographically close neurons w.r.t. location vectors also imply close neurons w.r.t. Euclidean distance. However, the adoption of a Kernel function over the distance of neurons in $\mathbb {R}^{2d}$ could assume query components to be isotropically Gaussian, which is not a general case when d is relatively large. The predicted cardinality $\hat {y}$ is estimated by a kernel smoothing of those cardinality prototypes and linear regression coefficients, whose associated neurons are topographically close (w.r.t. 𝜖) to the winner neuron.

Given actual y and predicted $\hat {y}$ in (10), we then adopt the loss functions:

$$ L_{1}(y,\hat{y}) = |y - \hat{y}| \text{ and } L_{2}(y,\hat{y}) = (y - \hat{y})^{2} $$

(11)

since there are widely used for evaluating the prediction error in cardinality prediction as in [11, 15, 27].

We can now provide the (on-line) learning phase of the model $\mathcal {M}$ given a sequence of pattern (training) pairs (q(1),y(1)),(q(2),y(2)),… Query patterns q(t) are used for quantizing the query space (over $\mathcal {L}$) and cardinalities y(t) are used for learning the q → y association (over $\mathcal {C}$ and $\mathcal {O}$). Upon the presence of a pattern pair (q(t),y(t)) the winner $\mathbf {w}_{j}(t) \in \mathcal {L}$ is determined by

$$ j = \arg \min_{\mathbf{w}_{i} \in \mathcal{L}} \lVert \mathbf{q}(t) - \mathbf{w}_{i}(t)\rVert. $$

(12)

After the projection of q to winner w _j , the model $\mathcal {M}$ updates in an incremental manner the winner and all its neighbors of lattice $\mathcal {L}$ such that they approach the query pattern q with a magnitude of β(t)h(i, j; t). In the same time, the actual cardinality y is used for updating the corresponding: (i) $y_{j} \in \mathcal {C}$ along with all prototypes $y_{i} \in \mathcal {C}$ and (ii) $\mathbf {m}_{j} \in \mathcal {O}$ along with all coefficients $\mathbf {m}_{i} \in \mathcal {O}$ associated with the neighbors of winner neuron w _j . Notably, the update rules for each y _i and m _i are governed by the loss function $L(y,\hat {y})$ we aim to minimize, having $\hat {y}$ defined in (10).

In the case of the neuron-cardinality lattices for cardinality prediction, the model $\mathcal {M}$ estimates the parameter α = ({w _i },{y _i })i= 1M by minimizing the objective function $\mathcal {J}_{1}$ in (13)

$$\begin{array}{@{}rcl@{}} \mathcal{J}_{1}(\{\mathbf{w}_{i}\},\{y_{i}\}) & = & \frac{1}{2}{\int}_{\mathcal{W}} \sum\limits_{\mathbf{w}_{i} \in \mathcal{L}}h(i,j)\lVert \mathbf{w}_{i} - \mathbf{q} {\rVert_{2}^{2}} \mathrm{d}p(\mathcal{W})\\ && + {\int}_{\mathcal{Y}} \sum\limits_{y_{i} \in \mathcal{C}} h(i,j) |y-\hat{y}| \mathrm{d}p(\mathcal{Y}) \end{array} $$

(13)

being taken over an infinite sequence of $\mathcal {W} = \{\mathbf {q}(1)$, q(2),…} and corresponding $\mathcal {Y} = \{y(1), y(2), \ldots \}$ and $p(\mathcal {W})$, $p(\mathcal {Y})$ is the pdf of $\mathcal {W}$ and $\mathcal {Y}$, respectively, with

$$ \hat{y} = \frac{{\sum}_{i = 1}^{M}\mathcal{K}_{\epsilon}(\lVert \mathbf{r}_{i} - \mathbf{r}_{j}\rVert)y_{i}}{{\sum}_{i = 1}^{M}\mathcal{K}_{\epsilon}(\lVert \mathbf{r}_{i} - \mathbf{r}_{j}\rVert)} $$

(14)

and $j = \arg \min _{\mathbf {w}_{i} \in \mathcal {L}}\lVert \mathbf {q}-\mathbf {w}_{i}\rVert _{2}$. The factor $\frac {1}{2}$ is for mathematical convenience. Here, we utilize the L ₁ in (11) loss function, since the cardinality prototypes are local scalar constant values within each query sub-space.

In the case of the neuron-regression lattices for cardinality prediction, the model $\mathcal {M}$ estimates the parameter $\alpha = (\{\mathbf {w}_{i}\},\{\mathbf {m}_{i}\})_{i = 1}^{M}$ by minimizing the objective function $\mathcal {J}_{2}$ in (15)

$$\begin{array}{@{}rcl@{}} \mathcal{J}_{2}(\{\mathbf{w}_{i}\},\{\mathbf{m}_{i}\}) \!&=&\! \frac{1}{2}{\int}_{\mathcal{W}} \sum\limits_{\mathbf{w}_{i} \in \mathcal{L}}h(i,j)\lVert \mathbf{w}_{i} \,-\, \mathbf{q} {\rVert_{2}^{2}} \mathrm{d}p(\mathcal{W})\\ &&\! + \frac{1}{2}{\int}_{\mathcal{U}} \sum\limits_{\mathbf{m}_{i} \in \mathcal{O}} h(i,j) (y\,-\,\hat{y})^{2} \mathrm{d}p(\mathcal{U}) \end{array} $$

(15)

where $p(\mathcal {U})$ is the pdf of m, with $j = \arg \min _{\mathbf {w}_{i} \in \mathcal {L}}\lVert \mathbf {q}-\mathbf {w}_{i}\rVert _{2}$ and

$$ \hat{y} = \frac{{\sum}_{i = 1}^{M}\mathcal{K}_{\epsilon}(\lVert \mathbf{r}_{i} - \mathbf{r}_{j}\rVert)\mathbf{m}_{i}^{\top}\mathbf{q}}{{\sum}_{i = 1}^{M}\mathcal{K}_{\epsilon}(\lVert \mathbf{r}_{i} - \mathbf{r}_{j}\rVert)}. $$

(16)

Here, we utilize the L ₂ in (11) loss function, since we estimate the local linear regression coefficients within each query sub-space based on the ordinary least squares method.

Theorem 1

Given a training pair (q(t),y(t)), the model $\mathcal {M}$ converges to the optimal parameter α , which minimizes the risk function $\mathcal {J}_{1}(\alpha )$ in(13) with respect to loss function $L_{1}(y,\hat {y}) = |y-\hat {y}|$ and $\hat {y}$ is defined in(14), if neuron $\mathbf {w}_{i}(t) \in \mathcal {L}$ and its associated prototype $y_{i}(t) \in \mathcal {C}$ are updated as:

$$\begin{array}{@{}rcl@{}} {\Delta} \mathbf{w}_{i}(t) &\,=\,& \beta(t) h(i,j; t) \left( \mathbf{q}(t) - \mathbf{w}_{i}(t) \right) \end{array} $$

(17)

$$\begin{array}{@{}rcl@{}} {\Delta} y_{i}(t) & \,=\, & \beta(t) \sum\limits_{k = 1}^{M}h(k,j; t) \frac{\mathcal{K}_{\epsilon}(\lVert \mathbf{r}_{i} - \mathbf{r}_{j}\rVert)}{{\sum}_{k = 1}^{M}\mathcal{K}_{\epsilon}(\lVert \mathbf{r}_{k} - \mathbf{r}_{j}\rVert)}\\ && \times \text{sgn}\left( y(t)-\hat{y}(t)\right) \end{array} $$

(18)

where sgn(⋅)is the signum function, β(t)is the learning rate and h(i, j; t)is the neighborhood function, j is the index of the winner neuron w _j (t)of pattern query q(t)and predicted $\hat {y}(t)$ is determined by(14).

The proof of Theorem 1 is provided in [5]; we present it here for self-contained reasons.

Proof

We derive the analysis of convergence corresponding to lattices $\mathcal {L}$ and $\mathcal {C}$. We verify whether the quantization error $\lVert \mathbf {w} - \mathbf {q} {\rVert ^{2}_{2}}$ and loss $L_{1}(y,\hat {y}) = |y-\hat {y}|$ actually decreases as the learning phase proceeds, converging eventually to a stable state.

The convergence is evaluated through the average expected loss $\mathcal {J}_{1}$ in (13) being taken over an infinite sequence of $\mathcal {W} = \{\mathbf {q}(1), \mathbf {q}(2), \ldots \}$ and corresponding $\mathcal {Y} = \{y(1), y(2), \ldots \}$ and $p(\mathcal {W})$, $p(\mathcal {Y})$ is the pdf of $\mathcal {W}$ and $\mathcal {Y}$, respectively. Since both pdfs are unknown and sequences $\mathcal {Y}$ and $\mathcal {W}$ are actually finite we use the Robbins-Monro (RM) stochastic approximation for $\mathcal {J}_{1}$ minimization to find an optimal value for each w _i , y _i , i = 1,…,M. Based on RM the stochastic sample J ₁(t) of $\mathcal {J}_{1}$ is $J_{1}(t) = \frac {1}{2}{\sum }_{\mathbf {w}_{i} \in \mathcal {L}}h(i,j;t)\lVert \mathbf {w}_{i}(t) - \mathbf {q}(t) {\rVert _{2}^{2}} + {\sum }_{y_{i} \in \mathcal {C}} h(i,j;t) |y(t)-\hat {y}(t)|$. The J ₁(t) has to decrease at each new pattern at t by descending in the direction of its (partial) negative gradient. Hence, the SGD rule for each w _i is ${\Delta } \mathbf {w}_{i}(t) = -\frac {1}{2}\beta (t)\frac {\partial J_{1}(t)}{\partial \mathbf {w}_{i}(t)}$ and for y _i is ${\Delta } y_{i}(t) = -\beta (t) \frac {\partial J_{1}(t)}{\partial y_{i}(t)}$, where β(t) satisfies ${\sum }_{t = 0}^{\infty }\beta (t) = \infty$ and ${\sum }_{t = 0}^{\infty }\beta ^{2}(t) < \infty$ [21]. From the partial derivatives of J ₁(t) we obtain the update rules (17) and (18) for parameter set α. □

Remark 1

Note that the update rule (18) for prototypes y _i (t) involves the current prediction $\hat {y}(t)$ of the model during the t-th training pair in the learning phase. Naturally we update each y _i (t) in an on-line supervised regression fashion, in which we take the prediction $\hat {y}(t)$ in (14) as feedback. From (18) we observe that neighbor y _i (t) of y _j (t) is adapted by its relative contribution provided by the kernel function, which is rational since y _i (t) contributes with the same magnitude to the cardinality prediction. If $y(t) > \hat {y}(t)$, then y _i (t) increases linearly with its contribution to prediction approaching the actual y(t). On the other hand, i.e., $y(t) < \hat {y}(t)$, y _i (t) decreases to move away from $\hat {y}(t)$ and approaches y(t). When the current prediction error is zero, i.e., $L(y(t),\hat {y}(t)) = |y(t)-\hat {y}(t)| = 0$, there is no update on the cardinality prototypes. Neuron w _i (t) moves toward pattern query q(t) to follow the trend. Obviously, the more similar a pattern query q and a neuron w _i are, the less w _i gets updated.

Theorem 2 refers to the convergence of a neuron w _i to the local expectation query representative, i.e., centroid $\mathbb {E}[\mathbf {q}|\mathbb {Q}_{i}]$ in the input sub-space $\mathbb {Q}_{i}$.

Theorem 2

If $\mathbb {E}[\mathbf {q}|\mathbb {Q}_{i}]$ is the local expectation query of the subspace $\mathbb {Q}_{i}$ and prototype w _i is the subspace representative, $P(\mathbf {w}_{i} =\mathbb {E}[\mathbf {q}|\mathbb {Q}_{i}]) = 1$ at equilibrium.

Proof

The update rule for a neuron w _i based on Theorem 1 is Δw _i ∝ (q −w _i ). Let the i-th neuron w _i reach equilibrium: Δw _i = 0, which holds with probability 1. By taking the expectation of both sides we obtain

$$\begin{array}{@{}rcl@{}} \mathbf{0} &=& \mathbb{E}[{\Delta} \mathbf{w}_{i}] = \mathbb{E}[(\mathbf{q}-\mathbf{w}_{i})] = {\int}_{\mathbb{Q}_{i}}(\mathbf{q}- \mathbf{w}_{i})p(\mathbf{q})\mathrm{d}\mathbf{q}\\ &=& {\int}_{\mathbb{Q}_{i}}\mathbf{q}p(\mathbf{q})\mathrm{d}\mathbf{q} - \mathbf{w}_{i}{\int}_{\mathbb{Q}_{i}}p(\mathbf{q})\mathrm{d}\mathbf{q}. \end{array} $$

This indicates that w _i is constant with probability 1, and then by solving $\mathbb {E}[{\Delta } \mathbf {w}_{i}] = \mathbf {0}$, the w _i equals the centroid $\mathbb {E}[\mathbf {q}|\mathbb {Q}_{i}]$. □

If 𝜖 is selected such that $\mathcal {K}_{\epsilon }(\lVert \mathbf {r}_{i} - \mathbf {r}_{j}\rVert ) = 0, i \neq j$, then we obtain Δy _j ∼sgn(y − y _j ) in which only y _j of the winner w _j is updated, given that there is no significant impact from other neighboring neurons after convergence, i.e., ${\sum }_{k = 1}^{M}h(k,j) \overset {t \to \infty }{=} h(j,j) \cong 1$. We then provide the following theorem:

Theorem 3

If $\tilde {y}_{j}$ is the median of the partition $\mathbb {Y}_{j}$ corresponding to the image of query sub-space $\mathbb {Q}_{j}$ of winner w _j then $P(y_{j} = \tilde {y}_{j}) = 1$ at equilibrium.

The proof of Theorem 3 is provided in [5]; we present it here for self-contained reasons.

Proof

Let y _j correspond to w _j and assume the image of $\mathbb {Q}_{j} \subset \mathbb {R}^{2d}$ to subspace $\mathbb {Y}_{j} \subset \mathbb {N}$ via the y = f(q). The median $\tilde {y}_{j}$ of $\mathbb {Y}_{j}$ satisfies $P(y \geq \tilde {y}_{j}) = P(y \leq \tilde {y}_{j}) = \frac {1}{2}$. Suppose that y _j has reached equilibrium, i.e., Δy _j = 0, which holds with probability 1. By taking the expectations of both sides and replacing Δy _j with the update rule sgn(y − y _j ):

$$\begin{array}{@{}rcl@{}} E[{\Delta} y_{j}] & = & {\int}_{\mathbb{Y}_{j}}\text{sgn}(y- y_{j})p(y)\mathrm{d}y \\ & = & P(y \!\geq\! y_{j}) {\int}_{\mathbb{Y}_{j}}p(y)\mathrm{d}y \,-\, P(y \!<\! y_{j}) {\int}_{\mathbb{Y}_{j}}p(y)\mathrm{d}y\\ &=& 2P(y \geq y_{j})-1. \end{array} $$

Since Δy _j = 0 thus y _j is constant, then $P(y \geq y_{j}) = \frac {1}{2}$, which denotes that y _j converges to the median of $\mathbb {Y}_{j}$. □

Theorem 4

Given a training pair (q(t),y(t)), the model $\mathcal {M}$ converges to the optimal parameter α , which minimizes the risk function $\mathcal {J}_{2}(\alpha )$ in(15) with respect to loss function $L_{2}(y,\hat {y}) = (y-\hat {y})^{2}$ and $\hat {y}$ is defined in(16), if neuron $\mathbf {w}_{i}(t) \in \mathcal {L}$ and its associated linear regression coefficients $\mathbf {m}_{i}(t) \in \mathcal {O}$ are updated as:

$$\begin{array}{@{}rcl@{}} {\Delta} \mathbf{w}_{i}(t) & = & \beta(t) h(i,j; t) \left( \mathbf{q}(t) - \mathbf{w}_{i}(t) \right) \end{array} $$

(19)

$$\begin{array}{@{}rcl@{}} {\Delta} \mathbf{m}_{i}(t) & = & \beta(t)\sum\limits_{k = 1}^{M}h(k,j; t) \frac{\mathcal{K}_{\epsilon}(\lVert \mathbf{r}_{i} - \mathbf{r}_{j}\rVert)}{{\sum}_{k = 1}^{M}\mathcal{K}_{\epsilon}(\lVert \mathbf{r}_{k} - \mathbf{r}_{j}\rVert)}\\ && \times \left( y(t)-\hat{y}(t)\right)[1; \mathbf{q}(t)]^{\top} \end{array} $$

(20)

where β(t)is the learning rate and h(i, j; t)is the neighborhood function, j is the index of the winner neuron w _j (t)of pattern query q(t)and predicted $\hat {y}(t)$ is determined by(16).

Proof

As in the proof of the Theorem 1, the convergence is evaluated through the average expected loss $\mathcal {J}_{2}$ in (13) being taken over an infinite sequence of $\mathcal {W} = \{\mathbf {q}(1), \mathbf {q}(2), \ldots \}$ and corresponding $\mathcal {Y} = \{y(1), y(2), \ldots \}$ and $p(\mathcal {W})$. We rest on RM stochastic approximation for $\mathcal {J}_{2}$ minimization to find an optimal value for each w _i , m _i , i = 1,…,M. The stochastic sample J ₂(t) of $\mathcal {J}_{2}$ is $J_{2}(t) = \frac {1}{2}{\sum }_{\mathbf {w}_{i} \in \mathcal {L}}h(i,j;t)\lVert \mathbf {w}_{i}(t) - \mathbf {q}(t) {\rVert _{2}^{2}} + \frac {1}{2}{\sum }_{\mathbf {m}_{i} \in \mathcal {O}} h(i,j;t) (y(t)-\hat {y}(t))^{2}$. Hence, the SGD rule for each w _i is ${\Delta } \mathbf {w}_{i}(t) = -\frac {1}{2}\beta (t)\frac {\partial J_{2}(t)}{\partial \mathbf {w}_{i}(t)}$ and for m _i is ${\Delta } \mathbf {m}_{i}(t) = -\frac {1}{2}\beta (t) \frac {\partial J_{2}(t)}{\partial \mathbf {m}_{i}(t)}$, where β(t) satisfies ${\sum }_{t = 0}^{\infty }\beta (t) = \infty$ and ${\sum }_{t = 0}^{\infty }\beta ^{2}(t) < \infty$ [21]. From the partial derivatives of J ₂(t) we obtain the update rules (19) and (20) for parameter set α. □

Remark 2

As seen in (20), when determining the positions of regression coefficients, supervised (prediction) error is not only taken into account, but also the input q and the impact of all neurons (reflected by their neighborhood functions h(k; j) are taken into consideration. Through this coupled training of the regression coefficients and neurons positions, query and regression representatives are placed in the input and output space, respectively, in such a way so as to minimize the loss function L ₂.

Remark 3

Let us assume again that an 𝜖 is selected such that $\mathcal {K}_{\epsilon }(\lVert \mathbf {r}_{i} - \mathbf {r}_{j}\rVert ) = 0, i \neq j$. Given that both neurons and regression coefficients converge from Theorem 4, then, we obtain the update rule: Δm _j ∼ (y −m j⊤q)q, given that there is no significant impact from other neighboring neurons after convergence, i.e., ${\sum }_{k = 1}^{M}h(k,j) \overset {t \to \infty }{=} h(j,j) \cong 1$; here, for mathematical convenience, we absorbed the ’intercept’ constant of the local regression plane by adding a constant dimension of one to q. Evidently, this corresponds to the stochastic update rule for the multivariate linear regression utilizing the ordinary least squares method.

The learning phase of model $\mathcal {M}$ is described in Algorithm 1. The input is the training set of pairs $\mathcal {Q} = \{(\mathbf {q},y)\}$, 2-dim. lattices $\mathcal {L}$ and $\mathcal {C}$ (or $\mathcal {O}$) with M entries, and a stopping threshold 𝜃 > 0. The algorithm processes successive random pattern pairs until a termination criterion T _t ≤ 𝜃. T _t is the 1-norm between successive estimates of neurons and cardinality prototypes:

$$ T_{t} = \sum\limits_{i = 1}^{M}\left( \lVert \mathbf{w}_{i}(t)-\mathbf{w}_{i}(t-1)\rVert_{1} + |y_{i}(t)-y_{i}(t-1)|\right), $$

(21)

or regression prototypes,

$$ T_{t} = \sum\limits_{i = 1}^{M}\left( \lVert \mathbf{w}_{i}(t)-\mathbf{w}_{i}(t-1)\rVert_{1} + \lVert \mathbf{m}_{i}(t)-\mathbf{m}_{i}(t-1)\rVert_{1}\right), $$

(22)

with $\lVert \mathbf {w}_{i} \rVert _{1} = {\sum }_{k = 1}^{2d}|w_{ik}|$ and $\lVert \mathbf {m}_{i} \rVert _{1} = {\sum }_{k = 1}^{2d + 1}|m_{ik}|$. The output is parameter set α.

4.5 Set cardinality prediction

Once the parameter set α is trained (for both output lattice variants), and thus no more updates are realized on neurons, cardinality prototypes and local regression coefficients, we predict the cardinality $\hat {y}$ given a random query q as defined in (14) and (16). That is, we proceed with answer set cardinality estimation without executing the incoming query q.

Firstly, the query q is projected onto the neuron lattice $\mathcal {L}$ and its winner w _j is obtained. In the case of the cardinality lattice $\mathcal {C}$, the corresponding cardinality prototype y _j is the associated constant of the query sub-space $\mathbb {Q}_{j}$. In the case of the regression lattice $\mathcal {O}$, the local regression coefficient m _j is obtained. The predicted COUNT value is $\hat {y}$ calculated by the Kernel regression over the region around the images f _i (q) = y _i in lattice $\mathcal {C}$ and $f_{i}(\mathbf {q}) = \mathbf {m}_{i}^{\top }\mathbf {q}$ in lattice $\mathcal {O}$, respectively, such that $\mathcal {K}_{\epsilon }(\lVert \mathbf {r}_{i} - \mathbf {r}_{j}\rVert ) > 0$, for i = 1,…,M.

4.6 Computational complexity

During the learning phase of the model $\mathcal {M}$, we require to (i) find the closest (winner) neuron over the neuron lattice $\mathcal {L}$ and then (ii) update all M prototypes in both input and output lattices based on the neighborhood weight h(i, j),∀i. This requires O(d M) space and O(d M) for the updates. Since prototypes are updated during learning, the learning phase requires O(d/𝜃) [10] iterations to get T _t ≤ 𝜃. After learning, we obtain cardinality prediction in O(d log M) by applying an one-nearest neighbor search for the winner using a 2d-dim. tree structure over the neurons in $\mathcal {L}$. After locating the winner, then we just retrieve those neighboring neurons (constant number) which are determined by the Kernel neighboring function $\mathcal {K}_{\epsilon }$. In the case of updates, adaptation given a pair requires also O(d log M) time for searching for the winner. Hence, our proposed parametric model, after training, can provide prediction in O(d log M), which is independent of the size of the data $|\mathcal {B}|$ and the training set $|\mathcal {Q}|$, thus, being capable for scaling out predictive analytics tasks.

5 Implementation in Spark

We have implemented our model in the Spark system [32]. The reason behind this implementation is to explore how such models can be incorporated into Big Data Engines. In addition, we examine how much faster and how close our cardinality estimations are, compared with the result obtained from the built-in COUNT method provided by these engines. This section covers the basic concepts behind Spark [32] (currently a popular Big Data engine) and an overview of how we developed and incorporated our machine learning model into Spark.

5.1 Overview of Spark

The Resilient Distributed Datasets (RDDs) lie in the foundation of Spark. RDDs are fault-tolerant distributed data structures that allow users to save intermediate results in main memory. This means that, RDDs can be easily recovered once something goes wrong and that they can be easily distributed in a cluster environment to improve efficiency. Their recovery is relied on the lineage graph produced by Spark. A lineage graph is a Directed-Acyclic Graph that is used to record all of the changes made to a dataset. Hence, once something goes wrong it can be easily re-computed using the steps recorded. In addition, through this functionality, the users can control the number of partitions to optimize the data placement and, also, offer a rich set of operations [32]. The set of operations can be divided into transformations and actions which are described as follows:

5.1.1 Transformations in Spark

The RDDs are created by loading data files from permanent storage or by using transformations on loaded data. These transformations can change the loaded data through operations such as filter and map. A comprehensive list of the available transformations can be found at Spark’s website.² It is worth noting that transformations are not applied immediately. Instead, Spark uses a lineage graph and pipelines successive transformations to the original dataset once an action is called [32].

5.1.2 Actions in Spark

Spark contains a type of methods called actions. These operations return a value to the application or export data into storage [32]. Example of those types of actions are:

• 1. COUNT, which refers to the exact cardinality of a given query and corresponds to our ground truth for assessing the cardinality predictability of our model;

• 2. COLLECT, which returns a list of elements given a query;

• 3. SAVE, which stores the RDD into a permanent storage, e.g., HDFS or a local file system.

5.2 Machine learning model implementation

For UCL (Task 1), we implement the online SOM algorithm with M neurons. We make use of the neurons input lattice concept $\mathcal {L}$ described in Section 4.2.1 and we implement our UCL approach to partition the query space as described in Section 3.1.1. The neuron input lattice $\mathcal {L}$ contains all of our neurons and the winner is determined and updated as in (1) making use of Stochastic-Gradient descent. For HCL (Task 2), we implement the supervised linear regression model making use of the coefficient output lattice $\mathcal {O}$ described in Section 4.2.3, in which the coefficients $\mathbf {m}_{j} = [m_{j0}, m_{j1}, \ldots , m_{j2d}] \in \mathbb {R}^{2d + 1}$ are associated with each query prototype $\mathbf {w}_{j} \in \mathcal {L}$. We then generate our predictions using Kernel regression in (16).

5.3 Range queries workload

In our implementation and experiments we dealt with multidimensional queries corresponding to a 2-dimensional data space (d = 2). The two boundary vectors are a = [a ₁, a ₂]^⊤ and $\mathbf {b} = [b_{1},b_{2}]^{\top } , a_{i}\leq b_{i}, a_{i},b_{i} \in \mathbb {R}$. Hence, in the experiments, a range query q is represented by a 4-dimensional row vector q = [a ₁, b ₁, a ₂, b ₂]. We further adjust this representation to ease up the process of generating our query set $\mathcal {Q}$. In this context, our resulting queries are of the form q = [c ₁, c ₂, l] with center $c_{i} = \frac {a_{i}+b_{i}}{2}$, and volume l = b _i − a _i , i = 1,…,d. Through this representation, each query q is a hyper-cube.

5.4 Cardinality prediction in Spark

To allow the execution of our model by Spark, we had to extend the main abstraction class RDD. (Note that the models we used or variations of them are available in MLlib.³) However, using these models was not possible when trying to extend the Spark-Core module because of a cyclic-dependency error between MLlib and Spark-Core. Therefore, we introduce some new methods to make use of our model. The main methods are as follows:

• 1. Training: This method trains our model given a list of executed range queries, i.e., the training set $\mathcal {Q}$. This Spark method is written in Scala:

  

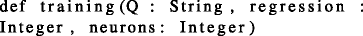
  where $\mathcal {Q}$ is the training set of queries, regression refers to the number of training queries to be considered for training the local linear regression models, and neurons refers to the number of neurons M in lattice $\mathcal {L}$ that partition the query-space.

• 2. Estimation: This method returns a cardinality estimation $\hat {y}$ given a range query q = [c ₁, c ₂, l]. This Spark method is written in Scala:

  

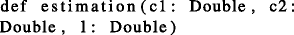
We also developed a number of helper methods to ease the execution of the two main methods.

• 1. Euclidean-Distance, which given two range queries, it calculates the Euclidean distance;

• 2. closest, which given a query q, it finds its closest neuron $\mathbf {w}_{j} \in \mathcal {L}$;

• 3. descent and movement, which update the winner neuron w _j w.r.t an incoming query q and learning rate β.

Executing our cardinality predictor in Spark involves two phases: the training and the prediction phase. The training phase is based on an input file containing the set $\mathcal {Q}=\{(\mathbf {q}_{i},y_{i})\}_{i = 1}^{n}$ corresponding to previously executed queries. The result of this phase generates an updated list of predicting the cardinality of incoming queries through the execution of the Estimation method. Executing these two phases in Spark involves loading up the dataset $\mathcal {Q}$ containing our previously executed queries into an RDD. For the training phase, we proceed using a map transformation to this set and create a new representation for query set $\mathcal {Q}$. The new representation, includes the corresponding closest neuron for each query q _i , i.e., $\mathbf {w}_{j}\in \mathcal {L}, j = \arg \min _{k \in [M]}\lVert \mathbf {q}_{i}-\mathbf {w}_{k} \rVert _{2}, \forall i$. Therefore, each tuple in the query set is now of the form $\mathcal {Q}=\{(\mathbf {q}_{i},y_{i},\mathbf {w}_{j})\}_{i = 1}^{n}$. To train the local linear regression models we iterate through all M neurons in lattice $\mathcal {L}$. For each neuron, we filter the query set $\mathcal {Q}$ such that we obtain a subset $\mathcal {Q}_{k} \subset \mathcal {Q}: \{(\mathbf {q}_{i},y_{i},\mathbf {w}_{j})\}_{i = 1}^{n} \text { and } j=k$. We then based on the subset $\mathcal {Q}_{k}$, train the associated linear regression models $f_{k}(\mathbf {q}) = \mathbf {m}_{k}^{\top }\mathbf {q}$. For the estimation phase, we do not require any transformations since the only thing we need are the coefficients m _j , j ∈ [M] for each one of the local linear regression models f _j (q) = m j⊤q; these are simply stored as global variables on runtime or in an external file.

Figure 4 shows the standard approach and our ML approach over Spark through an example where the actual cardinality y = 3678 as derived from the Spark’s COUNT. Specifically, we observe the dataset $\mathcal {B}$ of data points $\mathbf {x} \in \mathbb {R}^{d}$ being stored along with our training set $\mathcal {Q}$ holding training pairs of $\{(\mathbf {q}_{i},y_{i})\}_{i = 1}^{n}$ and our stored coefficients m from the coefficient lattice $\mathcal {O}$. Moreover, Figure 4 demonstrates how the COUNT is obtained using a standard approach with transformations and actions. It is worth noting that the standard approach requires expensive operations such as loading the whole dataset $\mathcal {B}$, filtering it in parallel and, then, executing a COUNT action. However, in our ML approach, we can skip this procedure and only incur the cost of loading our Coefficient lattice $\mathcal {O}$, or if our ML model was trained at runtime, we could already have this model stored as a global variable. We, then, proceed to predict the answer set cardinality $\hat {y}$ using inexpensive operations.

Fig. 4

The standard approach in obtaining the answer set cardinality y (COUNT) and our ML approach as a sequence of transformations and actions over the dataset $\mathcal {B}.$, which predicts the cardinality $\hat {y}$

6 Performance evaluation

We now turn to study the performance and accuracy of our implemented machine learning model in Spark. We measure the model’s accuracy using various metrics and also demonstrate how our model can be used to speed up joins in databases. In addition, we compare its average execution time and standard deviation with Spark’s own COUNT method over a standard file size. We also demonstrate the scalability of our solution by varying the file sizes. Finally, we measure the training time required by our machine learning model over different file sizes. Over the next sections, we introduce the evaluation metrics used and also explain how the training dataset was generated. Furthermore, we describe the experiment procedure followed and analyze the findings of our experiments.

6.1 Evaluation metrics

To evaluate our model we chose multiple evaluation metrics. These metrics are divided into two categories, accuracy and performance. Accuracy metrics help us determine whether the estimations generated by our model are close to the actual (true) values. These true values are obtained from the exact cardinality by invoking the COUNT Spark method. Performance metrics help us compare our solution with Spark’s own implementation of COUNT in terms of query processing time. In addition, they can help us identify bottlenecks in our solution when experimenting with different file sizes or parameters, thus, evaluating the scalability of our approach.

6.1.1 Cardinality prediction accuracy

The first accuracy metric for a prediction model is the Root Mean Squared Deviation (RMSD) which aggregates the magnitudes of the errors $(y_{i}-\hat {y}_{i})^{2}$ corresponding to the actual cardinality y _i and the predicted cardinality y _i of unseen query q _i for n prediction times:

$$RMSD = \sqrt{\frac{{\sum}_{i = 1}^{n}(\hat{y}_{i} - {y}_{i})^{2}}{n}}. $$

By adopting RMSD, we can examine how large our prediction errors are by using our model.

6.1.2 Coefficient of determination

The Coefficient of Determination R ² is calculated using the sum of squared residuals ${{\sum }_{i}^{n}}(y_{i}-\hat {y}_{i})^{2}$ and the total sum of squares ${{\sum }_{i}^{n}}(y_{i}-\bar {y})^{2}$ where $\bar {y}$ is the average cardinality value $\bar {y} = \frac {1}{n}{{\sum }_{i}^{n}}y_{i}$, i.e.,

$$R^{2} = 1 - \frac{{{\sum}_{i}^{n}}(y_{i}-\hat{y}_{i})^{2}}{{{\sum}_{i}^{n}}(y_{i}-\bar{y})^{2}}. $$

The R ² is a real number within [0,1] and indicates how closely the obtained approximation of $\hat {y} \approx f(\mathbf {q},\alpha )$ matches the actual cardinality y. The closer R ² is to 1, the better our model fits the data and is able to make accurate cardinality predictions.

6.1.3 Normalized RMSD (NRMSD)

A normalized version of RMSD is also used. Knowing the normalized RMSD helps us determine the ratio of the standard deviation to the mean. When calculated, its value is a percentage that indicates us how far off we are from the mean of the true cardinality values $\bar {y}$ we are trying to predict.

$$NRMSD = \frac{RMSD}{\bar{y}}. $$

6.1.4 Forecast interval

To get a better view of the dispersion between the predicted values $\hat {y}$ and the true values y we used the RMSD and NRMSD with the mean value of the true cardinality. By using the equations below we can see how much our estimation and the actual COUNT differ by orders of magnitude, i.e., by defining the intervals:

$$\bar{y} \pm RMSD, \qquad \bar{y} \pm NRMSD. $$

To effectively measure the performance of our solution, we conducted multiple experiments each time recording the time taken by different stages in our solution. The main aspects we wanted to measure was training time and execution time. Both of these are explained below.

6.1.5 Symmetric mean absolute percentage error (SMAPE)

The mean absolute percentage error (MAPE) for assessing the predictability capability of our model is not symmetric in the sense that interchanging $\hat {y}$ and y does not lead to the same answer. The cause of this asymmetry lies in the denominator of the MAPE formula: $\frac {|y-\hat {y}|}{y}$ dividing by the actual y instead of the predicted value $\hat {y}$ leads to a different result. This issue has been raised in [8] and [25]. Makridakis in [25] proposed a variation of the MAPE to provide symmetry and protected against outliers by dividing the absolute loss $|y-\hat {y}|$ by the arithmetic mean of the actual y and the predicted $\hat {y}$. This is known as the symmetric mean absolute percentage error (SMAPE):

$$SMAPE = \frac{100\%}{n}\sum\limits_{i = 1}^{n}\frac{|y_{i}-\hat{y}_{i}|}{y_{i} + \hat{y}_{i}} $$

SPAME provides a lower and an upper percentage bound, i.e., between [0,100]%, which is much easier to interpret adopting and due to its advantages of scale-independency.

Remark 4

Note that to evaluate the predictability of our model and fairly compare with the Spark’s COUNT built-in aggregation operator we adopt the above-mentioned metrics (RMSD, NRMSD, Coefficient of Determination, Forecast interval, and SMAPE), which align with the objective minimization prediction loss functions in the second part of (13) and (15). Recall, that we learning the query-cardinality association in light of minimizing the prediction loss in (11), thus, the SCP evaluation has to be consistent with these objective functions. Moreover, such prediction accuracy metrics are widely used for evaluating the prediction error in SCP as in [11, 15, 27].

6.1.6 Model training time

The recorded model training time is the time taken for our model to execute the SOM algorithm and then train the individual linear regression models for each neuron.

6.1.7 Query execution time

To be able to compare the performance of the COUNT method of Spark with our solution, the time required for each of the functions to return a result was measured.

6.2 Datasets & workloads

In Spark we used the real dataset RS4⁴ containing around 4 million 2-dimensional data (d = 2). The dataset contains sensor readings which were normalized and are bound within a range of [− 0.5,0.5]. This dataset was used to answer the cardinality range queries. We generate the training set $\mathcal {Q}$ and evaluation set $\mathcal {E}$, such that the evaluation set $\mathcal {E}$ is generated independently of $\mathcal {Q}$, thus, assuring completely unseen queries.

The training set size $|\mathcal {Q}| = s , s \in [10^{5},2 \cdot 10^{5},4 \cdot 10^{5}]$ and the number of neurons M = 20 for lattice $\mathcal {L}$ (and $\mathcal {C}$, $\mathcal {O}$). In addition, the evaluation set size $|\mathcal {E}| = 10^{3}$. The set $\mathcal {Q}$ contains a number of K query subspaces $\mathbb {Q}_{k} \subset \mathbb {R}^{2d}$. Each $\mathbb {Q}_{k}, k = 1,\ldots , K,$ is characterized by a query pattern-generator (c _k , v _k , ℓ _k ). The center of each q of $\mathbb {Q}_{k}$, for each dimension i, i = 1,…d, is sampled from a Gaussian distribution $\mathcal {N}(c_{ki},v_{ki})$ with mean c _{k i} , variance v _{k i} , and radius ℓ _{k i} ; i.e., lower bound a _{k i} = x _{k i} − ℓ _{k i} and upper bound b _{k i} = x _{k i} + ℓ _{k i} , center $x_{ki} \sim \mathcal {N}(c_{ki},v_{ki})$. The mean c _k for each dimension i was drawn uniformly at random, with c _k1 = [0.05,0.2] and c _k2 = [0.1,0.25]. The variance was constant for each subspace and at each dimension set to v _{k i} = 0.01. The volume of each query 2ℓ _{k i} is drawn uniformly at random from [0.01,0.05]. A random query q is then generated as follows: a $\mathbb {Q}_{k}$ is selected uniformly at random from K query spaces with equal probability $\frac {1}{K}$. Then, from $\mathbb {Q}_{k}$ we obtain the center (lower and upper values) and volume values for all attributes. Table 1 shows the parameters and the default values.

Table 1 Parameters

6.3 Performance assessment

The experiments were ran on a system with an i7 8-core processor and 6 GB RAM, under an Ubuntu 14.04 LTS OS. Spark (version 1.6) was setup in standalone mode working. We trained our models using the training method implemented over Spark. A number of experiments were executed and are outlined below:

• 1. Execute the evaluation set $\mathcal {E}$ against the dataset RS4 each time recording:

  • the cardinality value y from the Spark’s COUNT.

  • the predicted cardinality value $\hat {y}$ from our model.

  • the execution time for Spark’s COUNT method.

  • the execution time for our model.

• 2. Execute 100 queries over different file sizes: 1GB, 2GB, and 3GB and find the average execution time and its standard deviation for both COUNT over Spark and our model implementation.

• 3. Execute the model training method training 100 times over different file sizes and obtain the average training time. The training file sizes are: (i) ’Small File’ containing 1 ⋅ 10⁵ training pairs of queries and their cardinality values, (ii) ’Medium File’ containing 2 ⋅ 10⁵ training pairs of queries and their cardinality values, and (iii) ’Large File’ containing 4 ⋅ 10⁵ training pairs of queries and their cardinality values.

Using the results of these experiments, we were able to construct multiple graphs and run other side-experiments. We analyze our findings in the following section.

6.3.1 Accuracy experiments

Accuracy Experiment 1

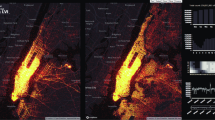
Table 2 shows the forecast interval, the RMSD value, the SMAPE value, and the coefficient of determination for our model. We present the actual and predicted cardinality in Fig. 5 (left) and a histogram, in Fig. 5 (right), showing the distribution of the difference $|y-\hat {y}|$ between our predictions $\hat {y}$ and the actual values y.

Table 2 Forecast interval for Experiment 1

As shown in Table 2, the true mean value for count is 91876 and our estimation is off at any time by around 10149 or 11% from the actual value for count. In addition, the coefficient of determination R ² = 0.99 indicating that our model fits the cardinality and query space significantly well and can proceed with accurate approximation of the y = f(q, α) function. Examining the Table 2 and the Fig. 5, we can determine the quality of accuracy of our predictions. Using these metrics, big data analysts can decide whether such estimations are acceptable with respect to the applications needs. Moreover, it is worth mentioning that the SMAPE value is 9% indicating the normalized symmetric absolute deviation from the actual cardinality value.

Fig. 5

(Left) The predicted $\hat {y}$ and actual y cardinality values; (right) histogram showing the distribution of the prediction error $y-\hat {y}$

Accuracy Experiment 2

Analyzing the results of Experiment 1, allowed us to gain some insight as to how accurate our predictions were. However, we wanted an effective way to measure whether such approximations are acceptable in applications we wish to use the proposed cardinality estimator. One of the ways our estimator can be used is for solving the selectivity estimation problem. Specifically, we examine our model from a qualitative perspective in the case where such an estimator can be used in query optimization. When joining two database relations, $\mathcal {R} \bowtie \mathcal {S}$, a common practice of optimized JOIN algorithms is to find the smaller relation in terms of cardinality and then perform the JOIN algorithm. In this case we need the cardinality of the two relations $\mathcal {R}$ and $\mathcal {S}$. In cases where the cardinality is unknown or $\mathcal {R}$ and $\mathcal {S}$ are intermediate relations, we need to perform a COUNT operation over both relations to find the smallest one. However, such an operation can be expensive especially in a Big Data environment. Hence, by adopting our SCP estimator, this operation can be performed at a fraction of the time. Our experiment measures the average false rate of our SCP estimator. By false rate, we mean the probability of our estimator being wrong about a comparison between the cardinalities of the two relations under the ⋈ operator. We use a zero–one loss function, which records the false rate for our SCP estimator. To be more precise, the ground truth value of a comparison, termed as Ground Truth Comparison (GTC) between the two relations comes from the actual system and from our SCP estimator. A comparison can have one of the following outcomes: (i) $|\mathcal {R}|>|\mathcal {S}|$; (ii) $|\mathcal {R}|<|\mathcal {S}|$; and (iii) $|\mathcal {R}|=|\mathcal {S}|$. If GTC and PRC are not in agreement for the outcome of a comparison then the false rate is incremented, otherwise it remains as is. By the end of our experiment we are left with a percentage denoting the probability of our estimator being incorrect when comparing two relations. For every result we got, we would compare it with the other N − 1 results we had. We would first compare the actual COUNT y and see which of the two queries had the largest cardinality. We would then compare their corresponding estimated cardinality result. The false rate provides insight on the degree of confidence on adopting our SCP methodology for the selectivity estimation problem in light of JOIN query optimization.

The Algorithm 2 explains this process with comparing the decisions coming from the GTC and our SCP method. The averaged false rate is 0.034342, which basically indicates that out of all the N − 1 = 999 query optimization decisions, that we made for each query, only 3% of them were false. That is, if our estimator was used to decide which relation is the smallest out of the ones involved in a JOIN, the smallest one would be found 97% of the time. A false rate of 3% indicates the upper qualitative degree of confidence for adopting our model in query optimization regardless of the quantified prediction error. This corresponds to the degree of confidence for using our SCP method for the selectivity estimation in JOIN queries without actually executing the query before the relational join ⋈ operator.

Accuracy Experiment 3

Figure 6(left) shows the RMSD error for our model against number of neurons M ∈ 5,10,20,30,50 for a constant number of query subspaces K = 20 over RS4 with d = 2. Our model achieves very low error as M increases indicating the need for an increased partitioning of our query-space. In addition, Fig. 6(right) demonstrates how an increase in M also affects how well our model $\mathcal {M}$ fits the underlying unknown function y = f(q, α). We note that for M > 20, the coefficient of determination does not change significantly suggesting that there is no need for introducing more neurons.

Fig. 6

(Left) The RMSD is improving by increasing the number of neurons M in lattice $\mathcal {L}$; (right) Coefficient Of Determination R ² improving after varying the number of neurons in lattice $\mathcal {L}$

6.3.2 Performance experiments

The next set of experiments were focused around the performance of our solution. This involved experiments to compare the execution time of the COUNT method over Spark and our method. In addition, we measured the performance of the training phase, which is essentially, the time required by the clustering process and the training of the linear regression models.

Performance Experiment 1

We measure the execution times obtained for Spark and our implementation by executing the evaluation set $\mathcal {E}, |\mathcal {E}|= 1000$ over RS4 holding 4 million rows. We record the time (ms) t _i required to obtain a value for COUNT for each query $\mathbf {q}_{i} \in \mathcal {E}$ and get the Mean Execution Time (MET) for both Spark and our model, i.e., $MET = \frac {1}{n} {\sum }_{i = 1}^{n}t_{i}$, with $n=|\mathcal {E}|= 1000$. We compare the two means M E T ₁ for Spark and M E T ₂ for our model and observe that we gain superior performance by approximately 4 orders of magnitude as M E T ₁ ≈ M E T ₂ ⋅ 10⁴. We also measure the Standard Deviation (SD) for the execution times of both Spark (S D ₁) and our model (S D ₂). The MET, SD, and median of the execution times are shown in Table 3. Again, we observe that the same pattern arising, showing that our model has less fluctuations in performance that Spark as $SD_{1} \approx \frac {1}{2}\cdot SD_{2} \cdot 10^{5}$. Therefore, it is safe to conclude that our solution provides a tremendous boost to big data applications and large-scale analytics tasks based on the cardinality of the analytics query answer sets.

Table 3 Performance comparison of Spark and our model

Performance Experiment 2

For the second performance experiment, we constructed two larger files from the original dataset $\mathcal {B}$ (RS4). We wanted to vary the size of the dataset to see the performance of our solution compared to Spark when the dataset size is increasing. We kept the original dataset and renamed it as ’Small Dataset’ (SD) with $|SD|=|\mathcal {B}|\approx 4 \cdot 10^{6}$. We then generated two more files, ’Medium Dataset’ (MD) and ’Large Dataset’ (LD) by replicating the existing rows by a factor of γ ∈{2,3}. In this context, we obtain: $|MD|=\gamma |\mathcal {B}|\approx 8 \cdot 10^{6}, \gamma = 2$ and $|LD|=\gamma |\mathcal {B}|\approx 1.2 \cdot 10^{7}, \gamma = 3$. The corresponding file sizes for these datasets are shown in Table 4. We, then, executed the evaluation set $\mathcal {E}$ over each data-set and obtained the MET for Spark’s COUNT method and our model as in Performance Experiment 1. The results of this experiment are shown in Fig. 7.

Table 4 File sizes

Fig. 7

Scalability: performance comparison of Spark and our method for different data set size (GB)

We can observe that as the file size gets larger the MET for COUNT over Spark exponentially grows. On the contrary, our model has relatively constant MET over all three files. The constant performance is due to the fact that our implementation does not need to execute any transformations or actions over Spark, thus, no computation or memory usage is required other than evaluating the linear regression model. This trend-line in Fig. 7 demonstrates how data size affects Spark and our solution. Evidently, this indicates the scalability capability of our model which is independent on the increase of the underlying data sizes.

Performance Experiment 3

In this performance experiment, we measured the time required for our model to pass through the training phase. Again, the number of neurons was set to M = 20. To better examine the training phase, we have created two larger training datasets. We left the original training set $\mathcal {Q}, |\mathcal {Q}|= 1 \cdot 10^{5}$ hereby referred to as ‘Small Query-set’ (SQ). Using the same process we generated a ’Medium Query-set’ (MQ), |M Q| = γ ^′⋅|Q| and a ’Large Query-set’ (LQ), |L Q| = γ ^′⋅|Q| where γ ^′∈{2,4}. The number of queries (and their corresponding actual cardinality values) contained in each file, along with the number of queries used for the SOM and the linear regression models training, are shown in Table 5. We run the training process 100 times over each file and obtain the Mean Training Time (MTT).

Table 5 Number of training pairs (query,cardinality)

The results of this experiment are shown in Fig. 8. We observe that the MTT grows exponentially with the size of the training dataset. Although, this might be a drawback of our implementation, it is a cost that will incur only once, as the training process is not required to run again unless the dataset changes. In addition, Fig. 8 shows the time required by the different stages in the training phase. The time allocated to Spark (‘Spark Op.’ in Fig. 8) refers to time not accounted for by our operations but allocated to Spark’s internal operations. The two stages concerned by our solution is SOM training and local linear regression training (LR in Fig. 8). It is clear that training the individual local linear models required longer time. However, the difference in time between the two stages is because of the larger amount of queries involved in the local linear regression training stage.

Fig. 8

Break down of the total Mean Training Time (MTT) over different file sizes in logarithmic scale; The mean training time consists of training for SOM, training for Local Linear Regression (LR) and allocated time for Spark Operations (Spark Op.)

7 Conclusions & future work

We introduce a novel perspective and solution for the problem of Set Cardinality Prediction. The fundamental unique characteristic of our approach is that it is query–driven. This is especially important for big data settings, as an increase in the underlying dataset size is largely inconsequential for our method’s efficiency and accuracy. The contributed neuron-based machine learning model (i) extracts knowledge from previous queries and their results, (ii) projects this knowledge onto two lattices (cardinality and coefficient lattices) of two self-organizing maps, and (iii) predicts the cardinality of the answer set. The model quantizes the query space and forms a cardinality and linear regression plane through learning the query-to-cardinality association. Our comprehensive experiments showcased the model’s robustness and that our model achieves very small error rates with small memory footprints outperforming the data-centric state-of-the-art. The proposed model represents the only solution applicable to general modern big data environments, which may include data nodes/owners placing access restrictions (e.g., for sensitive data) and/or where data accesses may be too costly to execute (e.g., in a cloud setting).

Our plans for future work focus on: (i) developing a framework that can dynamically and optimally switch between the training phases and query execution phases as analysts interests shift between data subspaces, and (ii) dealing with data spaces with on-line data mutations (insertions, deletions, and updates).

Appendix: Nomenclature

Notation	Explanation
$\mathcal {B}$	Dataset
$\mathcal {Q}$	Set of pairs (query,cardinality)
$\mathcal {E}$	Evaluation set
$\mathcal {L}$	Neuron lattice
$\mathcal {O}$	Coefficient output lattice
$\mathcal {C}$	Cardinality output lattice
M	Number of neurons
q	Range query vector
w	Neuron vector
m j	Coefficients vector for local linear regression, associated with neuron w j
$y \in \mathbb {N}$	Cardinality
$\mathcal {M}$	Machine learning model
β ∈ (0, 1)	Learning rate
r j = [r j,1, r j,2]	Location vector of neuron w j
h(i, j : t)	Neighborhood function
ρ	Width of the neighborhood function
α	Parameter set for model $\mathcal {M}$
Λ	Parameter space
$\hat {y}$	Predicted cardinality
$\mathcal {J}(\alpha )$	Risk function
$L(\hat {y}, y)$	Loss function
$\mathcal {N}_{k}(\mathbf {q})$	Set of the k-th closest queries to query q.
K 𝜖 (u)	Kernel function
𝜃	Stopping training threshold.
T t	1-norm between successive estimates of neurons and cardinality prototypes