4D modelling for rapid assessment of biventricular function in congenital heart disease

Abstract

Although more patients with congenital heart disease (CHD) are now living longer due to better surgical interventions, they require regular imaging to monitor cardiac performance. There is a need for robust clinical tools which can accurately assess cardiac function of both the left and right ventricles in these patients. We have developed methods to rapidly quantify 4D (3D + time) biventricular function from standard cardiac MRI examinations. A finite element model was interactively customized to patient images using guide-point modelling. Computational efficiency and ability to model large deformations was improved by predicting cardiac motion for the left ventricle and epicardium with a polar model. In addition, large deformations through the cycle were more accurately modeled using a Cartesian deformation penalty term. The model was fitted to user-defined guide points and image feature tracking displacements throughout the cardiac cycle. We tested the methods in 60 cases comprising a variety of congenital heart diseases and showed good correlation with the gold standard manual analysis, with acceptable inter-observer error. The algorithm was considerably faster than standard analysis and shows promise as a clinical tool for patients with CHD.

Appendix

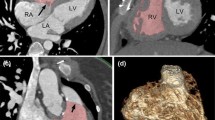
The position of any point on the model in Fig. 2 is given by:

$$\begin{aligned} \mathbf {x}(\xi _d) = \sum _{p}{\Psi _{p}(\xi _d)\mathbf {x}_{p}} \end{aligned}$$

(4)

where $\Psi$ are the basis functions, i.e. bicubic Bézier in $\xi _1$ and $\xi _2$ and linear in $\xi _3$.

Equation 1 was minimized by linear least squares, by solving the resulting normal equations $Ax=b$ using an iterative preconditioned conjugate gradient method. A matrix was decomposed into:

$$\begin{aligned} \mathbf A = \mathbf A _{data} + \mathbf A _{smoothing} + \mathbf A _{predicted points} \end{aligned}$$

(5)

An effective preconditioner is provided by the following [6]:

$$\begin{aligned} \Xi ^{-1} = (\mathbf A _{smoothing} + \mathbf A _{predicted points})^{-1} \end{aligned}$$

(6)

This preconitioner was chosen as it is similar to the A matrix and can be precalculated.

In order to find the D-Affine smoothing term (Eq. 3, Jacobian of motion can be calculated as follows:

$$\begin{aligned} J_{ij} = \tfrac{\partial x_{i}}{\partial X_{j}} = \sum _{l}{\tfrac{\partial x_{i}}{\partial \xi _{l}}\tfrac{\partial \xi _{l}}{\partial X_{j}}} = \sum _{l}{\tfrac{\partial u_{i}}{\partial \xi _{l}}\tfrac{\partial \xi _{l}}{\partial X_{j}}+\delta _{ij}}. \end{aligned}$$

(7)

The Kronecker delta is represented by $\delta _{ij}$. In the case of homogeneous affine motions, the Jacobian is constant, with respect to the model coordinates, and thus the resulting norm is zero. Therefore the D-Affine smoothing scheme penalizes deviations from affine deformations. In fact, $S(\mathbf u )$ is zero for any global affine transformation, and is therefore invariant to superimposed rigid body motions. It is also quadratic in the displacement parameters, leading to a linear least squares minimisation (each coordinate field being solved separately using the same system of equations). The derivative of the Jacobian is calculated by:

$$\begin{aligned} \frac{\partial {J}_{ij}}{\partial {\xi }_{k}} = \sum _{l}{\frac{\partial ^{2}x_{i}}{\partial {\xi }_{k}\partial {\xi }_{l}}}\frac{\partial {\xi }_{l}}{\partial {X}_{j}} + \frac{\partial {x}_{i}}{\partial {\xi }_{l}} \frac{\partial }{\partial {\xi }_{k}}\left[ \frac{\partial {\xi }_{k}}{\partial {x}_{j}}\right] \end{aligned}$$

(8)

Derivatives of the displacement field are given by:

$$\begin{aligned}&\mathbf x (\xi ) = \sum _{n}{\Psi _{n}(\xi )x_{n}} \end{aligned}$$

(9)

$$\begin{aligned}&\frac{\partial \mathbf{x }}{\partial {\xi }_{k}} = \sum _{n}{\Psi _{n,k}(\xi )x_{n}} \end{aligned}$$

(10)

$$\begin{aligned}&\frac{\partial ^{2}\mathbf{x }}{\partial {\xi }_{k}\partial {\xi }_{l}} =\sum _{n}{\Psi _{n,k,l}(\xi )x_{n}} \end{aligned}$$

(11)

where $\Psi _n$ are the basis functions, ($\Psi _{n,k}$ are derivatives with respect to the model coordinates, etc) and $\xi$ are the model coordinates. In order to calculate the smoothing terms in each element, we need the derivatives of Eq. 3 with respect to the $mth$ parameter in the $qth$ displacement field. Let:

Table 5 Condition values of tests 1 and 3 with different weights

$$\begin{aligned} g_{ij} = \frac{\partial {\xi }_{i}}{\partial {X}_{j}} = \left[ \frac{\partial {X}_{i}}{\partial {\xi }_{j}}\right] ^{-1} \end{aligned}$$

(12)

and

$$\begin{aligned} h_{ijk}= \frac{\partial }{\partial {\xi }_{k}}\left[ \frac{\partial {\xi }_{i}}{\partial {X}_{j}}\right] \end{aligned}$$

(13)

Components of the $\mathbf A _{smoothing}$ matrix can then be calculated using Gaussian quadrature from the derivatives of Eq. 3 with respect to the model field parameters:

$$\begin{aligned} \frac{\partial {S}}{\partial {u}_{mq}}= & {} 2\sum _{g}{w_{g}}\sum _{k}{\alpha _{k}}\sum _{j}\left\{ \left[ \sum _{l}{\sum _{n}{\Psi _{n,kl}u_{nq}g_{lj}}}\right. \right. \nonumber \\&\left. + \sum _{l}{\sum _{n}{\Psi _{n,l}u_{nq}h_{ljk}}}\right] \left[ \sum _{l}{\Psi _{m,kl}g_{lj}}\right. \nonumber \\&\left. \left. +\sum _{l}{\Psi _{m,l}h_{ljk}}\right] \right\} \end{aligned}$$

(14)

where $w_g$ are the Gauss point weights and the basis functions are evaluated at the Gauss point positions.

Since the optimum solution is found using a preconditioned conjugate gradient, the conditioning of the A matrix (Eq. 5) is important. Table 5 shows the condition number of $\Xi ^{-1}{} \mathbf A$ and number of PCG iterations required for tests 1 and 3. The condition numbers can be reproduced using different weights, where they have be scaled in the relationship of 10 for the predicted points and guide-points and $10^2$ for the smoothing term. The preconditioned conjugate gradient performed with a tolerance of $1\times 10^{-6}$ and a maximum of 100 iterations.

It was also noted that the numerical accuracy improved with increasing weights. The minimum absolute value (the smallest absolute number) in the A matrix was $2.7\times 10^{-12}$ for a smoothing weight of 0.0001, predicted point weight of 0.001 and guide-point weight of 0.0025. For a smoothing weight of 10,000, predicted point weight of 1 and the guide-point weight of 2.5 the smallest absolute value was $2.7\times 10^{-4}$. Since a type double (used in all experiments) will store up to 16 decimal places, increasing the minimum absolute value in the A matrix will reduce the effect of truncation errors.

The smoothing weighting must therefore be carefully chosen, considering (1) goodness of fit, (2) conditioning of $\Xi ^{(-1)} \mathbf A$, and (3) the size of the minimum absolute value. The minimum size of the matrix elements is important as the closer it is to machine precision, the greater the impact of truncation errors.