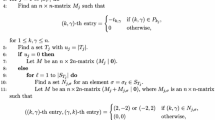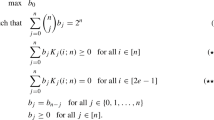Abstract
Let \(C\) be an extremal binary doubly even self-dual code of length \(n\) and \(D_{w}\) be the support design of \(C\) for a weight \(w\). We introduce the two numbers \(\delta (C)\) and \(s(C)\): \(\delta (C)\) is the largest integer \(t\) such that, for all wight, \(D_{w}\) is a \(t\)-design; \(s(C)\) denotes the largest integer \(t\) such that there exists a \(w\) such that \(D_{w}\) is a \(t\)-design. In this paper, we consider the possible values of \(\delta (C)\) and \(s(C)\).
Similar content being viewed by others
References
Alltop W.O.: Extending \(t\)-designs. J. Comb. Theory Ser. A 18, 177–186 (1975).
Assmus Jr E.F., Mattson Jr H.F.: New 5-designs. J. Comb. Theory 6, 122–151 (1969).
Bachoc C.: On harmonic weight enumerators of binary codes. Des. Codes Cryptogr. 18(1–3), 11–28 (1999).
Bannai E., Koike M., Shinohara M., Tagami M.: Spherical designs attached to extremal lattices and the modulo p property of Fourier coefficients of extremal modular forms. Mosc. Math. J. 6, 225–264 (2006).
Calderbank A.R., Delsarte P., Sloane N.J.A.: A strengthening of the Assmus–Mattson theorem. IEEE Trans. Inf. Theory 37, 1261–1268 (1991).
Delsarte P.: Hahn polynomials, discrete harmonics, and \(t\)-designs. SIAM J. Appl. Math. 34(1), 157–166 (1978).
Horiguchi N., Miezaki T., Nakasora H.: On the support designs of extremal binary doubly even self-dual codes. Des. Codes Cryptogr. 72, 529–537 (2014).
Horiguchi N., Miezaki T., Nakasora H.: Erratum to: “On the support designs of extremal binary doubly even self-dual codes”. Des. Codes Cryptogr. 73, 1027–1028 (2014).
Janusz G.J.: Overlap and covering polynomials with applications to designs and self-dual codes. SIAM J. Discret. Math. 13(2), 154–178 (2000).
Mallows C.L., Odlyzko A.M., Sloane N.J.A.: Upper bounds for modular forms, lattices, and codes. J. Algebra 36, 68–76 (1975).
Zhang S.: On the nonexistence of extremal self-dual codes. Discret. Appl. Math. 91, 277–286 (1999).
Acknowledgments
The authors wish to thank Masaaki Kitazume for helpful discussions in Chiba University. The authors also thank Eiichi Bannai for providing the reference [9]. The second author would like to thank Masaaki Harada for useful discussions in Tohoku University. This work was supported by JSPS KAKENHI (22840003, 24740031).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by V. D. Tonchev.
Rights and permissions
About this article
Cite this article
Miezaki, T., Nakasora, H. An upper bound of the value of \(t\) of the support \(t\)-designs of extremal binary doubly even self-dual codes. Des. Codes Cryptogr. 79, 37–46 (2016). https://doi.org/10.1007/s10623-014-0033-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10623-014-0033-7