Abstract
We consider environmental regulation in a context where firms invest in abatement technology under conditions of uncertainty about subsequent abatement cost, but can subsequently adjust output in the light of true marginal abatement cost. Where an emissions tax is the only available instrument, policy faces a trade-off between the incentive to invest in abatement technology and efficiency in subsequent output decisions. More efficient outcomes can be achieved by supplementing the emissions tax with direct regulation of abatement technology, or by combining the tax with an abatement technology investment subsidy. We compare the properties of these alternative instrument combinations.
Similar content being viewed by others
1 Introduction
It is well known that uncertainty about the costs of pollution abatement has implications for the choice between alternative forms of pollution regulation. Weitzman’s celebrated analysis (Weitzman 1974) sets out conditions under which regulation using a price-based instrument such as an environmental tax on emissions would be more or less efficient than regulation by quantity, such as a system of tradeable emission quotas. Developing this line of analysis, Roberts and Spence (1976) show that in fact a mixed instrument, combining elements of price and quantity regulation, would out-perform either price or quantity regulation alone. In particular, they demonstrate that the expected welfare costs of quantity regulation based on tradeable emission quotas will be reduced if supplemented by an element of price regulation, in the form of upper and lower bounds to the permitted range of permit prices. Judged against the ex post optimum this mixed regulatory regime–with appropriately-chosen parameters-performs better than either price or quantity regulation alone.
In this paper, we explore the implications of uncertainty for optimal environmental regulation in a context which extends, and in some respects contrasts with the approach taken by these earlier papers.
Like Roberts and Spence we are particularly interested in characterising cases where combined use of two regulatory instruments may be able to achieve outcomes which mitigate the potentially-extreme ex post inefficiencies that arise from dependence on a single regulatory approach. Unlike Roberts and Spence, however, we focus on cases where efficient quantity regulation, in the form of tradeable emissions quotas, is not an available option. This is a case of considerable practical relevance, especially in contexts where the number of firms to be regulated is too small to sustain a competitive market for tradable permits, or where the transactions costs of emissions trading are too high. We therefore focus on an initial regulatory approach based on an emissions tax, supplemented by other instruments with certain second-best limitations. Nevertheless it would be reasonable to anticipate that there would be some symmetry between our analysis and that of Roberts and Spence, and we explore the extent to which this is the case.
A second respect in which our analysis develops this earlier literature is that we provide a clearer characterisation of the uncertainties and informational asymmetries, and the way in which these constrain the operation of environmental regulation. Like this earlier literature we consider cases where uncertainty differentially affects governments and firms, and unlike policy-makers, the firms in our model are able to make certain decisions in the light of the true realised state. However, our model involves a richer set of decisions, which provide a clearer context for this asymmetry. In particular, both governments and firms are forced to make decisions about one form of abatement, based on long-term investment, before the uncertainty is resolved. Firms subsequently make a second decision affecting their emissions when they decide on their level of output, and this decision is made after the uncertainty has been resolved. We argue later that this context provides a clearer motivation for the presence of uncertainty, and its differential impact on policy and business decision-makers than the rather ad hoc uncertainty in the earlier literature.
The model we consider is one in which a regulatory agency seeks to control pollution from firms which produce a commodity that they sell at an exogenous price. The assumption that the price is exogenous allows us to neglect general equilibrium effects, and to focus on the issues of direct interest. We might for example think of this as a commodity which is traded in a global market, but other interpretations are possible.
We represent uncertainty in our model as uncertainty about the output price.Footnote 1 This is unknown to the authorities at the time the regulatory parameters are set, and is unknown to the firm at the time they make long-term irreversible investments in abatement technology, but firms make their output decisions based on the true price realisation. When the world price for the product is high, firms will wish to produce more, and their higher output generates additional pollution. To the extent that pollution abatement can be partly achieved through output reductions, a higher output price translates into a higher marginal cost of pollution abatement.
Uncertainty about the costs of pollution abatement can take different forms. One version involves once-and-for-all scenario in which at some future date a state of the world will unfold and then remain unchanged. At the time when policy decisions are made, it is uncertain which state of the world will emerge. With this form of uncertainty it is perhaps difficult to explain why policy cannot subsequently be adjusted in the light of actual circumstances, but a case for a once-and-for-all solution may still be made as argued by Roberts and Spence (1976, p. 193).Footnote 2 A second type of uncertainty arises in a “vibrating” system, in which there is frequent variation in states over time.Footnote 3 If policy cannot be adjusted rapidly enough to changing states, it will be necessary to set available instruments so as to maximise average social efficiency over time or across contingencies. A third interpretation of uncertainty in policy-making is actually an information asymmetry: the government lacks information about circumstances that are crucial for the effects of policy decisions—“inadequate information” or an “information gap” in the words of Weitzman (1974, p. 480.) In our model, we focus on forms of uncertainty that involve a clear temporal sequence rather than information asymmetry, but the uncertainty about the future could equally well be interpreted as a single uncertain event or a rapidly-changing sequence of randomly generated states.
Related literature includes a number of studies of instrument choice, and studies of irreversible abatement investment under uncertainty.
In the first category, Christiansen and Smith (2011) consider how second-best limitations on available instruments give rise to a case for combined use of multiple instruments, even in the absence of uncertainty. The instrument choice literature also includes discussion of the properties of relative emissions quotas—in other words, quotas defined relative to output - which will tend to encourage abatement, while having a lower impact on output decisions than absolute quotas. Ebert (1998) for example, considers a model of relative standards in a context with no uncertainty and identical firms. He characterises the optimal relative standard where it is the only instrument employed and shows that it is never equivalent to an optimally chosen environmental tax.
The literature on irreversibility in abatement investment includes a number of papers looking at the timing of abatement investments, assuming a stochastic time path for demand or output price (see e.g. Xepapadeas 2001, and Chao and Wilson 1993). In this context investors have the option to delay irreversible investment, and will choose to do so in states where prices are unfavourable. As a result, the market price for emissions allowances will exceed the marginal cost of abatement investment by an amount which can be interpreted as an option value. In our model, these issues do not arise, as we assume that a single investment (commitment) decision is made, and that the firm has no choice about timing.
Baldursson and Fehr (2004) set up a model where profits are uncertain due to uncertain future number of firms and uncertain polluting emissions prior to abatement. They consider a long-term irreversible investment under uncertainty and a short-term abatement decision after the uncertainty is resolved, with both decisions affecting polluting emissions. This is a distinction similar to ours. Most of the analysis is devoted to quota regimes, but they also briefly address a tax regime. By the assumptions of their model the marginal profitability of investment is deterministic, in contrast to the model we present in this paper. Due to this assumption, Baldursson and Fehr’s model achieves cost efficiency in emission reductions through the conventional result that all abatement activities are carried out up to the point where the respective marginal abatement costs are equated to the tax. This property does not hold in our model, and it is this which creates the case for combined use of multiple instruments
In the next section we set up the basic economic model, and we characterise the behaviour of firms in Sect. 3. In Sect. 4 we consider policy when the regulator is confined to using an emissions tax as the sole instrument. Sections 5 and 6 then show how the availability of an additional instrument, in the form respectively of regulation of abatement technology or subsidy to abatement investment, can improve the regulatory outcome. Section 7 draws some conclusions.
2 The Economic Setting
In our model there are a fixed number of firms which produce a homogeneous good, using a production process which generates emissions. Emissions can be reduced through initial investment in an abatement technology, and also by varying the level of output. These decisions are made at different times and with different amounts of information available:
-
At an initial stage, firms must commit to the abatement technology they will use while facing uncertainty about output price and the future output level to be chosen conditional on that price. At this stage the firm incurs any up-front costs of investment in the chosen abatement technology. In addition, adopting a more effective abatement technology at this stage will increase the subsequent cost of producing each unit of output. (Later in the paper, when we consider emissions taxes and other policy instruments, we will assume that these too must be set at this stage, in the face of uncertainty about output prices.)
-
At a subsequent stage, the output price is revealed, and firms make decisions about output levels in full knowledge of the output price and given their technology commitment from the initial stage. At this stage the firms incur the costs of production and of operating the abatement technology that they selected at the initial stage.
The strategy of a firm at the initial stage will be to look ahead to the subsequent stage and, for each possible abatement technology they could select at the first stage, consider how much to produce conditional on any price being revealed. The first-stage commitment to a particular abatement technology will affect the cost of producing each unit of output in the second stage, and will also affect the reduction in emissions that is achieved, for any given level of output. The firm will then base its initial abatement technology decision on the expected profits at the subsequent stage that will result from any initial decision.
One possible practical interpretation of our model is that it represents the type of decisions that have to be made about pollution abatement in the power sector. Typically, acid rain policies include some major investments in pollution abatement facilities at power stations, such as flue gas desulphurisation (FGD) “scrubbers”. These investments are large and irreversible, and have to be made in the face of uncertainty about many relevant variables, including the future level of the electricity price. They also significantly affect the costs of future operation, and hence of future changes in output and emissions. For example, data provided by Islas et al. (2005) on the initial capital costs and subsequent operating and maintenance costs for a range of \(\hbox {SO}_{2}\) abatement technologies indicate that the capital costs and additional operating costs for many such abatement technologies may be of broadly similar orders of magnitude. Where the electricity price in future is low, a power station that has selected an abatement technology involving high unit costs of operation might be able to reduce emissions more cheaply (ie at less sacrifice in terms of profit) by reducing its level of output than a power station that has chosen an equally-effective abatement technology where the costs are primarily those of the initial investment. For both, however, the amount of abatement that can be achieved through output reduction will be lower than for a “dirty” power station which initially chose a relatively cheap technology offering little abatement. In other words, the initial abatement technology decision, made before future prices are known, will have implications for the costs of reducing emissions during future operation.
We formalise our model in terms of a representative firm that produces \(x\) units of a good. The good is sold at an exogenous price \(p\), which is assumed to be stochastic with density \(f(p)\). Our assumption that the price is exogenous is made to avoid unnecessary complexity; it might, for example, be understood to reflect the case of firms which are price-takers in international trade. The (private) cost of production, neglecting abatement, is \(C(x)\). \(\gamma \) parameterises the choice of abatement technology, which is made in the first stage and is assumed to be irreversible; it reflects the reduction in emissions per unit of output. In the absence of any abatement activity \(\gamma =0\). Adopting an abatement technology, each unit of emissions is is reduced to a fraction \(1-\gamma \) of the no-abatement level. In general, \(0\le \gamma \le 1\). The cost of abatement is \(G(x,\gamma )\,+\,K(\gamma )\) where \(K(\gamma )\) is an initial cost, unrelated to subsequent output, and \(G(x,\gamma )\) is an operating cost of the abatement technology, which depends on the output level.
\(K(\gamma )\) is the fixed (ie output-independent) cost of installing the equipment needed to reduce the emission level to \(1-\gamma \). It turns out that what really matters in the subsequent analysis is whether \({K}'(\gamma )\) is zero or strictly positive. The former case may occur either because there is no payment at all up front or because the up-front payment is the same for all \(\gamma \). However, in order to limit the number of cases to consider, in what follows we shall simply refer to cases with and without a fixed cost. Where \({K}'(\gamma )>0\), we assume that \({K}''(\gamma )\ge 0\).
\(G(x,\gamma )\) is interpreted as the cost of applying the technology \(\gamma \) to \(x\) units of output. We assume that \(\partial G(x,\gamma )/\partial x{>}0, \partial G(x,\gamma )/\partial \gamma >0, \partial ^{2}G(x,\gamma )/\partial x^{2}{\ge } 0, \partial ^{2}G(x,\gamma )/\partial \gamma ^{2}>0\) and \(\partial ^{2}G(x,\gamma )/\partial x\partial \gamma >0\). Using the abatement technology is more costly the larger is the output to which it is applied and the higher is the abatement rate \(\gamma \) that it achieves.
In general, firms have different cost structures and may choose different output and abatement levels, and may therefore have different levels of emissions. Aggregate emissions across all firms are \(Z=\sum _i {(1-\gamma _i )x_i } \). The emissions give rise to an external cost which is assumed to be an increasing and strictly convex function of aggregate emissions expressed as \(D(Z)=D\left( {\sum _i {(1-\gamma _i )x_i } } \right) \) where \({D}'>0\) and \(D{''}>0\). The external cost is increasing in output (\(x_i )\) and decreasing in abatement effort (\(\gamma _i\)).
Given our assumptions, the social surplus arising from the activities of the firms is the gross output value net of social (private and external) costs, which equals
Emissions can be diminished either by increasing \(\gamma \) or reducing output, \(x\). The marginal cost of abatement by reducing \(x\) is \(p\,-\,{C}'_i \,-\,\partial G_i /\partial x_i \) which is stochastic due to the randomness of \(p\).
In the interest of tractability and ease of exposition, we shall consider special cases adopting simple functional forms in parts of the paper. We define one of these as follows:
-
Special case S1 Linear private and social marginal cost functions. We set \(C(x)=cx^{2}/2\) where \(c\) is a positive parameter, and \(G(x,\gamma )=k(\gamma )x\), where \({k}'>0\) and \({k}''>0\). The former assumption is the widely-adopted simplification that marginal production cost is linear in output. The latter assumption is that there is a fixed cost of operating the abatement equipment per unit of output to which it is applied. The unit cost will be larger where a more advanced technology is operated.
The equivalent expression to (1) in the special case S1 is
The marginal cost of abatement by reducing \(x\) in this case is \(p-c_i x-k_i (\gamma )\).
3 Producer Behaviour
In this section we characterise the behaviour of producers, who are subject to a tax \(\tau \) per unit of emissions, set irrevocably by the government prior to the time at which producers commit to their initial decisions about the abatement technology they will employ, \(\gamma \). Recall that when the firms must make their abatement technology decision they are uncertain about the output price, but that their subsequent output decisions are made after the output price is known.
The profits of each producer \(i\) will be
After the price uncertainty has been resolved, the firm chooses an output level to maximise profits conditional on the \(\gamma _i\). This yields the first order condition
and the second order condition
The first order condition implicitly defines \(x_i \) as a function of \(\gamma _i \) and \(\tau :x_i (p,\tau ,\gamma _i )\).
Prior to the price uncertainty being resolved, expected profits are
where E denotes the expectations operator. Inserting \(x_i (p,\tau ,\gamma _i )\), yields \(E\left( {\Pi _i } \right) \) as a function of \(\gamma _i\) and \(\tau \). The firm chooses \(\gamma _i \), the abatement technology, to maximise expected profits. This yields the first order condition
where the Envelope Theorem has been invoked. The second order condition is
Doing comparative statics to analyse the effect of a tax change, we first differentiate (4) with respect to \(\tau \) to find the effect of the tax for a given abatement technology. We get
and it follows that \(\frac{\partial x_i }{\partial \tau }<0\). Differentiating (4) wrt \(\gamma _i \) we find
The effect will depend on the sign of \(\frac{\partial ^{2}G_i }{\partial x_i \partial \gamma _i }-\tau \). There are two potentially conflicting effects. When a better abatement technology is chosen an increase in output will generate less additional pollution, and add less to the tax liability, which will stimulate production. However, choosing a better abatement technology will make production more costly.
Differentiating (6) to explore the effect of the tax on the choice of abatement technology, we find
allowing for the fact that \(x_i \) is a function of \(\tau \). We note that there are conflicting effects. A larger emission tax will increase the tax savings from further abatement and stimulate investment in abatement technology. The effect is larger the larger is expected output. Secondly, a larger tax will lower output and hence the amount of pollution affected by improved abatement technology, making it less worthwhile to invest. Finally, a lower output will reduce the operating cost of using a better abatement technology, inducing more investment.
Now consider the special case of the cost functions S1 introduced above, where \(G(\gamma ,x)=k(\gamma )x\),
Also setting \(C(x)=cx^2 /2\), we now get, for firm \(i\),
and it follows that
and
The first order condition for the choice of \(\gamma _i \) now becomes \(\left( {\tau -k_i ^{\prime }(\gamma _i )} \right) E(x_i )-{K}'_i (\gamma _i )=0\), so that
implying that \(\partial x_i /\partial \gamma _i \ge 0\). Firms will choose the same abatement technology if all cost elements are the same in all firms, i.e. \(k_i ^{\prime }(\gamma ),{K}'_i (\gamma _i )\) and \(c_i \) do not vary across firms. We also note that if \({K}'_i =0\), and the cost of abatement is the same in every firm, \(k_i (\gamma )=k(\gamma )\), all firms will choose the same technology \(\gamma \) given by \(\gamma ={k}'^{-1}(\tau )\). This will hold even if production costs differ, in other words, if firms have different values for \(c_i \).
Inserting the special case S1 in (9), we get
As in the general case, we have the opposing effects on \(d\gamma _i /d\tau \) considered above. However, in the case S1 where \({K}'_i =0\), we get \(\tau -k_i ^{\prime }(\gamma _i )=0\) and \(d\gamma _i /d\tau =1/{k}''_i (\gamma _i )>0\). In this case it also follows that \(\partial x_i /\partial \gamma _i =0\). The output level is independent of the abatement technology, because the tax saving and the cost effect cancel out.
In order to limit the number of possible cases to investigate, we will assume that a larger tax will stimulate investment in abatement technology, \(d\gamma _i /d\tau >0\). This assumption applies for the remainder of the paper, in both specific and general cases, as this seems the more plausible case.
Finally, consider the total effect of \(\tau \) on \(x_i\) allowing for the fact that the tax will affect output both directly and indirectly via the effect on investment in abatement technology: \(\frac{dx_i }{d\tau }=\frac{\partial x_i }{\partial \tau }+\frac{\partial x_i }{\partial \gamma _i }\frac{\partial \gamma _i }{\partial \tau }\).
Due to the ambiguity of \(\partial x_i /\partial \gamma _i \), the sign of \(dx_i /d\tau \) is also ambiguous. The immediate impact of a higher tax is to reduce output, but investment in a better abatement technology may stimulate output because of the lower emission tax liability.
We can now summarise the various behavioural responses.
In the general case we find the following: For a given choice of abatement technology, \(\gamma \), a higher tax will diminish output: \(\partial x/\partial \tau <0\). Improving the abatement technology will have ambiguous effects on the output level as it will lower the tax burden but increase the cost of production. Where the choice of abatement technology is endogenous a higher tax will have conflicting effects both on the choice of abatement technology and output.
For the special functional forms S1 in which private and social marginal cost functions are linear we find \(\frac{\partial x}{\partial \tau }\) and \(\frac{dx}{d\tau }=\frac{\partial x}{\partial \tau }+\frac{\partial x}{\partial \gamma }\frac{\partial \gamma }{\partial \tau }\) are independent of \(p\). Where \({K}' >0\) we find that \(\frac{\partial x}{\partial \gamma }>0\). Where \({K}'=0\) we find \(\frac{\partial x}{\partial \tau }=0,\frac{dx}{d\tau }=\frac{\partial x}{\partial \tau }+\frac{\partial x}{\partial \gamma }\frac{\partial \gamma }{\partial \tau }=0, \frac{\partial x}{\partial \gamma }=0\) and \(\frac{\partial \gamma }{\partial \tau }>0\). Where the initial abatement technology decision involves a non-zero sunk investment cost, a more effective abatement technology leads to increased output.
4 The Government Sets \(\tau \) Only
In this and subsequent sections we consider various government policies. We start with the case where the government sets an emissions tax but does not directly interfere with the producer’s choice of abatement technology. Our assumption is that this tax must be set prior to output price uncertainty being resolved, and that it then must remain fixed. In setting the emissions tax \(\tau \) the government takes into account that this will affect the producer’s choice of output once the price becomes known, and also the producer’s choice of abatement technology prior to knowing the price.
The government maximises the expected social surplus
Differentiating with respect to \(\tau \), we get
which must be equated to zero at the optimum. Making use of (4) and (6), we obtain
An alternative formulation is
where \(dx_i /d\tau =\partial x_i /\partial \tau +(\partial x_i /\partial \gamma _i )(\partial \gamma _i /\partial \tau )\).
Making use of standard statistical concepts, we can reformulate terms as follows
In the absence of uncertainty, the pollution tax would be set equal to the marginal external damage. The question is whether, in the presence of uncertainty, we would wish to set the pollution tax equal to the expected marginal external damage: \(\tau =E({D}')\). If the marginal damage, \({D}'\), is constant across states, we would indeed wish to do so. In this case the cost function would be linear rather than convex. However, where the marginal damage varies across states, the outcome will be improved by setting the tax so that it provides a greater marginal incentive in the states where the marginal damage is greatest.
To consider what this implies, we take the tax set at the rate of expected marginal external damage as a point of departure. We get
Where output is larger, the marginal external cost is larger and the first covariance in this expression is positive. Under the assumption that the tax stimulates investment in abatement technology, the first main term is then positive. The intuition for this sign is that investment in abatement technology will have a larger impact the larger is the scale of polluting production and accordingly the marginal external cost.
In general we cannot tell how the tax effect on output varies across states. We note that where the marginal output response to the tax \(\left( {dx_i /d\tau } \right) \) is non-increasing in output level, i.e. the polluting output is reduced more (or increased less) when the marginal external cost is larger, \(\hbox {cov}\left( {{D}',dx_i /d\tau } \right) \le 0\). This would obviously be true both in a linear case and in an isoelastic case, and appears to be a plausible assumption. Then both terms in (18) would be non-negative.
We can draw the following conclusion.
Proposition 1
\(C\hbox {ov}\left( {{D}',dx_i /d\tau } \right) \le 0\) is a sufficient but not a necessary condition for the Pigouvian tax to be optimally set above the expected marginal external damage: \(\tau >E({D}')\). This condition will hold in the special case S1.
Setting the tax equal to the expected marginal damage does not allow for the fact that due to the convexity of the damage function the benefit from diminishing the external cost is larger in states where emissions are larger. Inducing further investment in abatement technology will have the effect of directing more of the emission reductions to those states since a better abatement technology will have a larger impact where it affects a larger number of units of output. This effect is reflected by the first of the terms in (18). If in addition the impact of the tax directly on output is larger in those states (the second covariance in (18) is negative) there will be a benefit from increasing the tax beyond the average effect equal to the expected marginal damage.
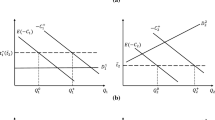
Since the damage function is strictly convex in total output, the expected value of the damage reduction from investment in abatement technology will exceed the expected tax savings of the producer, so there will be underinvestment in abatement from the social perspective. There is a social gain from further investment, not allowed for by the private investor. To encourage greater abatement investment—and hence greater emissions reductions in states where marginal damage is large—the tax must be set above the expected marginal damage. The drawback is that there will then be a downward distortion of output for a given abatement technology as the external cost is now being over-internalised.Footnote 4 For a given investment level, the output is too small. Where a tax is the only instrument it cannot simultaneously achieve both the desired output level and the desired investment. The optimum is characterised by a trade-off between the concerns with output and investment.
In formal terms, this is demonstrated by (17), where the overall effect of the tax is broken down into the direct effect on output and the effects of the induced change in abatement technology, where the latter in turn consists of the effect via output and the abatement effect on emissions for a given output. Where \(\tau >E({D}')\), as highlighted in Proposition 1, the first main term in (17) is negative reflecting excessive output reduction. Where (17) is equated to zero at the pure tax optimum, this negative effect must be offset by a positive marginal effect of abatement investment at the optimum, as captured by the remaining terms. In this sense there will be a combination of “underproduction” and “underinvestment” at the optimum, and alleviating one of the distortions can only be achieved by aggravating the other. In other words, partial increases in output and investment, would both be socially desirable but not achievable by a tax alone. In the next section we will discuss opportunities for realising these gains by using the tax and direct regulation of technology as separate instruments.
5 The Government Sets \(\tau \) and \(\gamma \)
Where cost functions are identical across firms, producers will obviously choose the same value of \(\gamma _i\). This is of course an extremely strict assumption, and in general \(\gamma _i\) will vary across firms. However, where the special functional forms S1 apply, and there is no payment up front, a sufficient condition for a uniform value of \(\gamma _i\) is simply that the cost function \(k_i(\gamma _i )\) is the same for all firms. This may be a reasonable assumption where a new abatement technology becomes available and is widely adopted.
Consider the case with uniform \(\gamma \) where the government can set \(\tau \) and \(\gamma \). Maximisation of the expected social surplus then implies the first order conditions
where (4) has been invoked.
which is equivalent to
Assuming \(\frac{\partial x_i }{\partial \tau }\) is constant across states, and accordingly \(\hbox {cov}\left( {{D}',\frac{\partial x_i }{\partial \tau }} \right) =0\), as in our special case S1, we get from (19) that \(\tau =E({D}')\). Also assuming that \(\partial x_i /\partial \gamma _i \) is invariant across states, we can then write:
The benefit from increasing \(\gamma \) consists of an expected reduction in external cost and a gain from directing the reductions towards cases where they are more highly valued (as captured by the covariance). This benefit must be traded off against the cost of adopting and running a more advanced abatement technology.
As \(E\left( {\partial G_i /\partial \gamma } \right) +E\left( {K_i ^{\prime }} \right) \)is increasing in \(\gamma \), we can see that \(\gamma \)will be larger where the expected marginal damage is larger, and where the marginal damage varies more strongly across states with different output levels.
We can summarise our findings as follows
Proposition 2
Where the government can determine both the emission tax and the abatement technology, and the tax effect on output is uniform across states, the tax is optimally set equal to the expected marginal damage.
Where the effect of abatement technology on output is constant across states, the optimal abatement technology is characterised by the benefit-cost trade-off
\(\gamma \) will be larger where the expected marginal damage is larger, and where the marginal damage varies more strongly across states with different output levels.
To shed further light on the effects, we consider the following special case, S2:
-
Special case S2 There is no payment up front, \(K_i ^{\prime }=0\). The cost structure is the same in all firms and given by the special functions S1 considered above: \(C(x)=cx^{2}/2\) and \(G(x,\gamma )=k(\gamma )x\). We also assume that the damage (external cost) function has the form \(D(Z)=D\left( {\sum _i {(1-\gamma _i )x_i } } \right) \quad =\frac{1}{2}eZ^{2}=\frac{1}{2}e\left( {\sum _i {(1-\gamma _i )x_i } } \right) ^{2}\) where \(e\) is a positive parameter, and \(Z\) denotes aggregate emissions.
In these circumstances,
as we know from above that \(\tau =E\left( {{D}'} \right) \), and (20) is equivalent to
It follows that
The left hand side is increasing in \(\gamma \). It follows that \(\gamma \) is larger the larger is the damage parameter \(e\), and \(\gamma \) is larger the larger is the variance of X for a given expected value. The latter finding is easy to understand since the beneficial property of the investment is that its impact is stronger where output and (marginal) damage are larger, and this is accentuated when the output level does indeed vary a lot across states.
Proposition 3
In case S2 where the government sets the emission tax, \(\tau \), and regulates the abatement technology \(\gamma \), the optimal use of the instruments is characterised by \(\tau =E\left( {e\sum _j {(1-\gamma )x_j } } \right) \) and \(k^{\prime }(\gamma )=e(1-\gamma )E\left( {\left( X \right) ^{2}} \right) /E\left( X \right) \). The tax is set equal to the expected marginal damage, and the investment in abatement technology is set to reflect the output (and damage) variance across states.
In the discussion above we have been considering the case where it makes sense to set a uniform abatement technology \(\gamma \). Where, however, there is heterogeneity among firms, there will be a case for variation in abatement technology. A uniform standard will then involve inefficiencies, but might still outperform a regime based on tax alone. However, optimally-differentiated direct regulation of the abatement technology of each individual firm to reflect firm-level heterogeneity is likely to be difficult to implement. For this case, therefore, we turn our attention to the use of subsidies to stimulate investment in abatement technology.
6 Subsidising Investment in Abatement Technology
In the discussion above we have shown that relying solely on an emissions tax to achieve abatement will require the tax to be set above the level of expected marginal damage, and that a better outcome, with investment in more-effective abatement technology, could be achieved by supplementing the emissions tax with a second instrument, in the form of direct regulation of abatement technology. In this section, we consider an alternative, market-based, approach, in which the second instrument takes the form of a subsidy to abatement investment. Such subsidy schemes exist or are often proposed either as explicit subsidies or in the form of a tax rebate to reward abatement.Footnote 5
We consider two kinds of subsidy to acquisition of abatement technology. The first, which we denote \(S\), is an “abatement cost” subsidy, taking the form of a payment in proportion to any fixed cost of investing in abatement technology, \(SK_i \left( {\gamma _i} \right) \). The second, which we denote \(s\), is an “output-scaled” abatement subsidy, \(s\gamma _i x_i\). We may note that since \(\gamma _i\) is a measure of abatement per unit of output \(\gamma _i x_i\) is a measure of firm i’s volume of abatement when its output is \(x_i\). In other words, the output-scaled subsidy is paid in proportion to the emission reduction achieved by the technology at the subsequent output level.
We begin by returning to (17) above, which we can formulate as
In order to limit the number of possible cases to address, we shall confine our attention to the case where the first line of (17’) is negative, as it will be in the special case S1 considered above.
and
In the subsidy regime, profits are given by
The first and second order conditions for the producer’s optimal choice of \(x_i \) and \(\gamma _i \), respectively, are
and
Comparative statics yield
We see that
It is obvious from (26) that
We consider first the case of the abatement cost subsidy \(S\). We can see that \(S\) will have no direct impact on firms’ output levels, i.e. \(x_i\) will remain unchanged for fixed \(\gamma _i\). However, the induced change in \(\gamma _i\) will affect \(x_i\).
Starting from the case where there is no subsidy, we consider the effect of adding a small subsidy. Allowing S to deviate slightly from zero gives the following effect on the expected surplus:
where the sign is due to assumption (23) above. This is an unsurprising result in view of our discussion above. The effect of S is to induce beneficial investment in abatement technology without directly affecting output.
We now consider the output-scaled abatement subsidy \(s\). This takes the form of a payment, per unit of abatement, based on the emissions reduction achieved by the chosen abatement technology, given the firm’s actual level of output. The subsidy payment provides encouragement to abatement investment, but at the same time provides an incentive for subsequent output. A change in \(s\) will affect \(x_i\) both directly via the cost of production and indirectly via the induced change in \(\gamma _i \). If we again take as point of departure the no-subsidy case, \(s=0\), comparative statics yields the following:
In general, the marginal increase in subsidy has opposing effects. A larger \(s\) will lower the private cost of investment and make it more profitable. It will also lower the cost of production and enhance output, which in turn makes it more profitable to invest in abatement technology. However, a larger output will enhance the operating cost of better technology and make the technology more costly. We assume that the last effect will not outweigh the other more direct effects.
Departing from the pure tax optimum, the question is what can be obtained by means of the subsidy beyond what is already achieved by the tax. This is easily demonstrated by making use of the initial optimality condition \(\partial E(\psi )/\partial \tau =0\), allowing us to write:
Making use of the fact that \(\partial x_i /\partial s=-\frac{\gamma _i }{1-\gamma _i }\partial x_i /\partial \tau \) and \(\frac{\partial \gamma _i }{\partial s}=\frac{\partial \gamma _i }{\partial \tau }\), we get
where the sign is due to (22).
The subsidy \(s\), unlike \(S\), will directly affect output in addition to investment. Indeed, it will stimulate output, which is a beneficial effect as initially the tax depresses output below the desirable level as a side effect of using the tax to induce investment. The effect on investment is no different from the effect of the tax on investment. The difference is that in contrast to the tax the subsidy will stimulate output and therefore it is that output effect that appears in (32).
Proposition 4
Where an optimal emission tax is used in the absence of regulation of abatement technology the social surplus can be enhanced by introducing one of two forms of subsidy to investment in abatement technology, a percentage subsidy to investment expenditure on abatement technology, \(S\), or an output-scaled subsidy s. Both stimulate investment in abatement technology, while avoiding the excessive incentive for output reduction which arises when using the emissions tax as the sole instrument. In particular, the output-scaled abatement subsidy \(s\) acts to stimulate output as well as investment, while the abatement investment subsidy S only acts through its impact on investment.
To compare a subsidy and direct regulation, now consider the \(s\) subsidy with our special cost functions S1, assuming no up-front payment and uniform \(k_i =k\), which is the case in which imposing a uniform abatement standard would be most appropriate. Given our assumed subsidy scheme the profits of each producer \(i\) are
As before, the producer is assumed to maximise profits after the price uncertainty has been resolved. Maximising profits with respect to output yields
\(\gamma _i \) is chosen to maximise expected profits, which requires that
implying that \(\gamma _i =\gamma ={k}'^{-1}(\tau +s)\).
Moreover it follows that
which confirms that \(\tau \) and \(s\) have the same effect on the choice of abatement scale \(\gamma \). The fact that subsidising abatement technology provides a stimulus to choosing larger abatement scale that is no different from that of an emission tax may throw doubt on the gains from adding this instrument. Moreover a tax discourages polluting production while a subsidy makes production cheaper and increases output, which is the well-known disadvantage of subsidising abatement rather than taxing emissions. However, as we realised above, the combined use of the two instruments can yield additional benefits.
It is possible to show that using the proper combination of the emissions tax and subsidy instruments can in fact reproduce the allocation achieved by means of direct regulation and a tax. Denote this allocation by \(\gamma \!{*}\) and \(x_i{*}\) (for all \(i\)) and denote by \(\tau \!{*}\) the optimal tax used in conjunction with direct regulation. We use the notation \(\tilde{\tau }\) and \(\tilde{s}\) for the tax and the subsidy when that combination is being used. From (34) we see that to obtain \(\gamma \!{*}\) one has to set \(\tilde{\tau }+\tilde{s}={k}'(\gamma \!{*})\). Combining the supply functions for the two cases from (10) and (33) we have that in order to obtain \(x_i{*}\) we must have
which requires that \(\tilde{\tau }(1-\gamma \!{*})-\tilde{s}\gamma \!{*}=\tau \!{*}(1-\gamma \!{*})\). Adding this to \(\tilde{\tau }+\tilde{s}={k}'(\gamma \!{*})\) then gives us two equations to determine the instruments needed to implement the same allocation as the one achieved with a tax and direct regulation. We note that \(\tilde{\tau }=\tau \!{*}+\tilde{s}\gamma \!{*}/(1-\gamma \!{*})\). The interesting implication is that when deploying a subsidy rather than direct regulation the tax will be set at a higher rate.
Proposition 5
In the special case S1 and assuming no up-front payment and uniform \(k_i =k\), the same second best optimum can be achieved by using either a combination of an emission tax and direct regulation of abatement technology, or alternatively a higher emission tax combined with an “output-scaled” subsidy to investment in abatement technology.
7 Conclusions
It is well known that uncertainty about the costs of emissions abatement can establish a case for combined use of different regulatory instruments, such as price-based regulation through an emissions tax and quantity-based regulation through a tradeable emissions quota (Roberts and Spence 1976). In this paper we have considered a different case for combined use of multiple instruments under conditions of uncertainty, in which the regulator seeks to influence a once-for-all abatement investment decision, while being uncertain about the costs of further abatement opportunities that arise in the course of subsequent operation. We suggest that the temporal sequence of decisions that must be taken provides a more natural framework for characterising abatement cost uncertainties.
The conventional wisdom, based on deterministic cases, is that where an emissions tax reflects the external cost, firms will choose the appropriate balance between different forms of abatement—in other words, initial investment in abatement technology and subsequent abatement through output reductions in the course of operation will both be employed up to the point where the respective marginal cost of abatement equals the emissions tax rate. In these cases there is no need for the tax to be supplemented by instruments bearing directly on abatement investment. We show that the optimal policy may be different when future abatement costs are uncertain or fluctuate over time, and the tax instrument is insufficiently flexible to be adjusted to all conceivable circumstances.
In the model we have described in this paper, both firms and the regulator face initial uncertainty about future output prices, and hence about the cost of abatement through future output changes. If the emissions tax is employed as the sole instrument and set at the level of expected marginal external damage, as would be optimal in the absence of uncertainty, there will normally be ex post inefficiencies, since the tax will provide the same incentive for abatement in states of the world in which emissions are large and damage is high as it provides in states where damage is lower. Ideally we would like an instrument which provides particular encouragement to abatement in states of the world where damage is high. If state-adjusted taxes are not available, the tax will normally need to be set above the level of expected marginal external damage, to induce further investment in abatement technology, which has the effect of directing more of the emissions reductions to states of the world where emissions, and hence marginal damage costs, are higher. However, the tax achieves this at the cost of encouraging excessive abatement through output reductions in subsequent operation.
Given the inefficiency of regulation through a fixed emissions tax alone, we have considered whether combined use of multiple instruments can improve the regulatory outcome. First, we have demonstrated that if it were possible to directly regulate the abatement technology decisions of firms, efficient abatement investment could be achieved with less damage to output levels than with the tax alone. However, efficient direct regulation, differentiated to take account of the costs of individual firms, is likely to have very high informational requirements that would in practice rule this option out. Uniform direct regulation of abatement decisions might be more feasible in practice, but would involve a trade-off: a better adjustment to ex post costs, but inefficient distribution of abatement across heterogeneous firms.
A market-based alternative, better able to reflect the costs of individual firms, would be to pay subsidies to abatement investment. We have considered two forms of subsidy, one which pays a percentage of the cost of abatement investment, and the other which pays an amount based on the effectiveness of the abatement technology employed and the subsequent output level of the firm (measured as the emission reduction achieved by the technology at the subsequent output level). We show that under conditions of uncertainty it will always be desirable to supplement an emissions tax with a subsidy to abatement, rather than to rely on the emissions tax alone. If used as the sole instrument the tax would have to be set at a level which can lead to an excessive subsequent reduction in output, so that the externality is over-internalised for a given abatement technology. As the tax and the subsidy have the same effect on investment in abatement technology but differ in their effect on output, the gain from introducing a subsidy is that it mitigates the excessive output effect without weakening the incentive to invest in abatement technology. Likewise, using a subsidy on its own would have the well-known disadvantage that it would encourage polluting emissions by lowering the cost of production and hence raising output. However, when the two instruments are deployed together, the output stimulus from the subsidy becomes a virtue, in that it acts to offset the excessive discouragement of output when the tax is set at the level necessary to achieve adequate abatement investment.
Finally, we compare the outcome that can be achieved with the combined use of an emissions tax and subsidy with the second-best optimum based on the emissions tax and optimally-differentiated regulation. Here we have confined our discussion to the case where firms would choose uniform gamma, avoiding the complexity issue. We show that, if the second form of subsidy is employed, it would be possible to achieve the same second-best optimum as with the tax and regulation. When combined with the subsidy, the emissions tax would be set at a higher rate than when combined with direct regulation.
Notes
A similar representation of abatement cost uncertainty appears in Quirion (2005), who compares separately the merits of three possible policy instruments, a tax, an absolute emissions cap, and a relative emissions cap.
“...we are rejecting the idea that the government can ‘feel out’ the ‘optimum’ by successively announcing and revising its policies...” “Given these circumstances, we have opted for the once-and –for –all-problem...” Op. cit. p. 193.
This is a possibility alluded to by Weitzman (1974): He refers to “elements of genuine randomness” (op. cit. p. 480) and adds: “like day-to-day fluctuations” (op. cit. footnote 1).
The tax-inclusive cost facing the producers will overstate the social cost of production (including the external cost).
Rajah and Smith (1993).
References
Baldursson FM, Von der Fehr N-HM (2004) Price volatility and risk exposure: on market-based environmental policy instruments. J Environ Econ Manage 48(1):682–704
Chao H-P, Wilson R (1993) Option value of emission allowances. J Regul Econ 5(3):233–249
Christiansen V, Smith S (2011) Externality-correcting taxes and regulation. Scand J Econ 114(2):358–383
Ebert U (1998) Relative standards: a positive and normative analysis. J Econ 67(1):17–38
Islas J, Manzini F, Grande G, Pérez M (2005) SO2, NOx, and particle control technologies and abatement costs for the Mexican electricity sector final report 00142, Centre for Energy Research (CIE). UNAM, México
Quirion P (2005) Does uncertainty justify intensity emission caps? Resour Energy Econ 27(4):343–353
Rajah N, Smith S (1993) Taxes, tax expenditures, and environmental regulation. Oxf Rev Econ Policy 9(4): 41–65
Roberts MJ, Spence M (1976) Effluent charges and licenses under uncertainty. J Public Econ 5(3–4):193–208
Weitzman ML (1974) Prices vs. quantities. Rev Econ Stud 41(4):477–491
Xepapadeas A (2001) Environmental policy and firm behaviour. In: Carraro C, Metcalf GE (eds) Behavioral and distributional effects of environmental policy: abatement investment and location decisions under uncertainty and irreversibility. University of Chicago Press, IL
Zhao J (2003) Irreversible abatement investment under cost uncertainties: tradable emission permits and emission charges. J Public Econ 87(12):2765–2789
Acknowledgments
We are grateful to two anonymous referees for comments on an earlier version of this paper. A previous version of the paper was presented at the 67th Congress of the IIPF in Ann Arbor. We are grateful to Beat Hintermann and other participants for comments. Christiansen’s contribution to the paper is part of the research at the ESOP Centre and Oslo Fiscal Studies at the Department of Economics at the University of Oslo, supported by the Research Council of Norway.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Christiansen, V., Smith, S. Emissions Taxes and Abatement Regulation Under Uncertainty. Environ Resource Econ 60, 17–35 (2015). https://doi.org/10.1007/s10640-013-9755-7
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10640-013-9755-7