Skip to main content
SpringerLink
Log in

Frequency and Severity Modelling Using Multifractal Processes: An Application to Tornado Occurrence in the USA and CAT Bonds

  • Published:
Environmental Modeling & Assessment Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

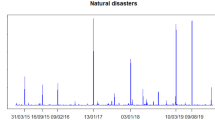
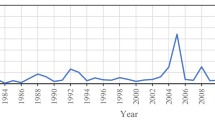
This paper proposes a statistical model for insurance claims arising from climatic events, such as tornadoes in the USA, that exhibit a large variability both in frequency and intensity. To represent this variability and seasonality, the claims process modelled by a Poisson process of intensity equal to the product of a periodic function, and a multifractal process is proposed. The size of claims is modelled in a similar way, with gamma random variables. This method is shown to enable simulation of the peak times of damage. A two-dimensional multifractal model is also investigated. The work concludes with an analysis of the impact of the model on the yield of weather bonds linked to damage caused by tornadoes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Notes

  1. http://webra.cas.sc.edu/hvriapps/sheldus_setup/sheldus_login.aspx

References

  1. Barrieu, P., & Scaillet, O. (2010). “A primer on weather derivatives.” In: Filar, Jerzy A. and Haurie, Alain, (eds.), Uncertainty and environmental decision making: A handbook of research and best practice. International series in operations research & management science (138) (pp. 155-176). Springer US, doi: 10.1007/978-1-4419-1129-2_5.

  2. Schmock, U. (1999). “Estimating the value of the Wincat coupons of the Winthertur insurance convertible bond.” A study of the model risk. ASTIN Bulletin, 29(1), 101–163.

    Article  Google Scholar 

  3. Barrieu, P., & Dischel, R. (2002).“Financial weather contracts and their application in risk management.” Chapter in Climatic Risk and the Weather Market, Risk Book, Risk Waters Group.

  4. Lopez Cabrera, B. (2010). “Weather Risk Management: CAT bonds and weather derivatives.” PhD Dissertation, Humboldt Universitaet, Berlin. http://edoc.hu-berlin.de/dissertationen/lopez-cabrera-brenda-2010-04-27/PDF/lopez-cabrera.pdf.

  5. Vaugirard, V. (2003). Valuing catastrophe bonds by Monte Carlo simulations. Applied Mathematical Finance, 10, 75–90.

    Article  Google Scholar 

  6. Lee, J. P., & Yub, M. T. (2007). Valuation of catastrophe reinsurance with catastrophe bonds. Insurance: Mathematics and Economics, 41(2), 264–278.

    Google Scholar 

  7. Alaton, P., Djehiche, B., & Stillberger, D. (2002). On modelling and pricing weather derivatives. Applied Mathematical Finance, 9, 1–20.

    Article  Google Scholar 

  8. Campbell, S., & Diebold, F. (2005). Weather forecasting for weather derivatives. Journal of American Statistical Association, 100(469), 6–16.

    Article  CAS  Google Scholar 

  9. Dornier, F., & Queruel, M. (2000). "Caution to the wind." Risk Magazine, EPRM, July, pp. 30-32.

  10. Benth, F. E., & Benth, J. S. (2007). The volatility of temperature and pricing of weather derivatives. Quantitative Finance, 7(5), 553–561.

    Article  Google Scholar 

  11. Benth, F. E., & Benth, J. S. (2009). The volatility of temperature and pricing of weather derivatives. Quantitative Finance, 7(5), 553–561.

    Article  Google Scholar 

  12. Hainaut, D. (2012). “Pricing of an insurance bond, with stochastic seasonal effects.” Bulletin Français d'actuariat. Juillet 2012.

  13. Chiera, B. A., Filar, J. A., Zachary, D. S., & Gordon, A. H. (2010). “Comparative Forecasting and a test of Persistence in the El Nino Southern Oscillation” In: Filar, Jerzy A. and Haurie, Alain, (eds.), Uncertainty and environmental decision making: A handbook of research and best practice. International series in operations research & management science (138) (pp. 255-273) Springer.

  14. Lovejoy, S., & Schertzer, D. (2007). Scale, scaling and multifractals in geophysics: Twenty years on. Nonlinear dynamics. In: A. A. Tsonis, J. Elsner (Ed.), Geosciences (pp. 311-337). Springer.

  15. Sachs, D., Lovejoy, S., & Schertzer, D. (2002). The multifractal scaling of cloud radiances from 1m to 1km. Fractals, 10, 253–265.

    Article  Google Scholar 

  16. Tchiguirinskaia, I., Schertzer, D., Lovejoy, S., & Veysseire, J. M. (2006). Wind extremes and scales: multifractal insights and empirical evidence, In: EUROMECH Colloquium on Wind Energy, edited by P. S. Eds. J. Peinke, Springer-Verlag.

  17. Calvet, L., & Fisher, A. J. (2008). "Multifractal volatility. Theory, forecasting and pricing". Academic Press. Elsevier.

  18. Resnick, S., & Samorodnitsky, G. (2003). Limits of on/off hierarchical product models for data transmission. The Annals of Applied Probability, 13(4), 1355–1398.

    Article  Google Scholar 

  19. Mu, M., & Zheng, Q. (2005). Zigzag oscillation in variational data assimilation with physical "on-off" processes. Monthly Weather Review, 133.

  20. Brody, D. C., Syroka, J., & Zervos, M. (2002). “Dynamical pricing of weather derivatives”. Quantitative Finance 2, p. 189-198.

    Google Scholar 

  21. Mandlebrot, B. (1982). "The fractal geometry of nature". Freeman.

  22. Mandelbrot, B. (1997). Fractals and scaling in finance: Discontinuity, concentration, risk. Berlin: Springer Verlag.

    Book  Google Scholar 

  23. Mandlebrot, B. (2001). Scaling in financial prices: Multifractals and the star equation. Quantitative Finance, 1, p124–p130.

    Article  Google Scholar 

  24. Major, J. A., & Lantsman, Y. (2001). "Actuarial applications of multifractal modeling part 1: Introduction and spatial applications." Non-refereed Paper of the Casualty Actuarial Society Forum.

  25. Jung, R. C., & Tremayne, A. R. (2011). Useful models for time series of counts or simplywrong ones? AStA Advances in Statistical Analysis, 95(1), 59–91.

    Article  Google Scholar 

  26. Bremaud, P. (1981). Point processes and queues martingales dynamics. New York: Springer Verlag.

    Book  Google Scholar 

  27. Lecki, T. R., & Rutkowski, M. (2004). "Credit risk: Modeling, valuation and hedging". Springer Finance.

  28. Hamilton, J. D. (1989). A new approach to the economic analysis of nonstationary time series and the business cycle. Econometrica, 57(2), 357–384.

    Article  Google Scholar 

  29. Kalman, R. E. (1960). A new approach to linear filtering and prediction problems. Journal of Basic Engineering, 82(1), 35–45.

    Article  Google Scholar 

  30. Calvet, L., & Fisher, A. J. (2001). Forecasting multifractal volatility. Journal of Econometrics, 105, 27–58.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Rennes Business School-CREST, Rennes, France

    Donatien Hainaut

  2. Département de mathématiques, UQAM, Québec, Canada

    Jean-Philippe Boucher

Authors
  1. Donatien Hainaut
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jean-Philippe Boucher
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Donatien Hainaut.

Appendix A.

Appendix A.

Proving the fractal nature of the number and cost of claims can be done by a visual analysis of autocovariance in levels. For any integrated process Z (number or cost of claims), the autocovariance in levels is defined as:

$$ {\delta}_Z\left(t,q\right)= Cov\left({\left|Z\left(a,\varDelta t\right)\right|}^q,{\left|Z\left(a+t,\varDelta t\right)\right|}^q\right) $$

and which quantifies the dependence of the size of increments

$$ Z\left(a+t,\varDelta t\right)=Z\left(a+t\right)-Z(t)\left|q\right. $$

such that statistical moments exist. Calvet and Fisher [30] show that multifractal processes have hyperbolically declining autocovariances in levels when t/Δt → ∞. In Fig. 8, these autocovariances (q = 2) are plotted for N t  − λ(t) and for C t  − τ(t). Autocovariances are well hyperbolically decreasing. The same trends are observed if q = 3.

Fig. 8
figure 8

Autocovariances in levels for different time lags

Full size image

Rights and permissions

Reprints and permissions

About this article

Cite this article

Hainaut, D., Boucher, JP. Frequency and Severity Modelling Using Multifractal Processes: An Application to Tornado Occurrence in the USA and CAT Bonds. Environ Model Assess 19, 207–220 (2014). https://doi.org/10.1007/s10666-013-9388-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10666-013-9388-9

Keywords

Search

Navigation