1 Introduction

Classical random walk (RW), as a significant tool, is omnipresent in natural sciences and social sciences, and has been utilized to solve a great deal of problems, including estimation of the volume of a convex body [1], graph connectivity [2], approximating the permanent of a non-negative matrix [3]. Recently, this concept was generalized to the quantum scenario by several groups [4–10], namely quantum walk (QW), in the hope of developing new quantum algorithms. After that, QW has attracted a lot of attention of researchers and has achieved a tremendous success in various applications, such as quantum state transfer [11, 12], graph isomorphism testing [13–15], constructing quantum Hash scheme [16, 17], and image encryption [18]. There are two major types of quantum walks, discrete-time quantum walk (DTQW) [7] and continuous-time quantum walk (CTQW) [8]. The key difference between them is that DTQW has an extra coin system. In addition, DTQW evolves at discrete time intervals, while CTQW at any time. In this paper, we restrict our attention to DTQW.

During the study of discrete-time quantum walk, one-dimensional two-state homogeneous DTQW has been extensively studied. In a simplest model, a quantum walker carries a two-sided quantum coin taking values, left and right. At each step, a so-called coin operator firstly acts only on coin state. Then, the walker moves one step backward or forward according to the outcome of the coin state, which can be implemented by a so-called shift operator. In this way, the system evolves step by step. Later, quantum walk is studied deeply and generated to several cases, e.g., multiple coins [19], multiple walkers [20], time-dependent coin [21]. As one important extension, one-dimensional three-state homogeneous Grover DTQW (called “G3 DTQW”) was first introduced by Inui et al. [22]. In this model, the walker can stay at the same position during a time step. Compared to the two-state model, this model exhibits some distinct properties. The most intriguing one is the localization effect, that is, the walker can be found in the vicinity of the the initial position with a nonzero probability even in the limit of infinite number of steps. In 2012, Štefaňák et al. [23] put forward two kinds of generalized G3 DTQW. One is a parametrization of eigenvectors of the Grover coin, called “G3- ρ DTQW”. The other is a parametrization of eigenvalues of the Grover matrix, called “G3- φ DTQW”. The localization effect can be observed in the two models. However, the localization effect disappears for some initial states. Recently, the above three kinds of localizing quantum walks are intensively studied in the literatures [24–31].

Another interesting extension of one-dimensional two-state quantum walk is presented by Wójcik et al. [32] and this model displayed an astonishing localization effect. Afterwards, considerable attention has been paid to this subject both theoretically [28, 33–38] and experimentally [39]. Although the localization effect can be observed in both G3- ρ DTQW and this quantum walk, the causes are different. The reason of G3- ρ DTQW is that the evolution operator has a non-empty point spectrum [23, 24], whereas that of the second one is the spatial perturbation. Obviously, we cannot help attempting to know what may happen if these two extensions are combined. In this paper, a three-state quantum walk with a phase defect at a designated position is proposed. In this manner, the effect of a single-point phase defect (SPPD) on the G3- ρ DTQW is discussed via considering three quantities, position probability distribution, position standard deviation, and the time-averaged probability at the designated position added the phase.

The rest of the paper is organized as follows. In the next section, a definition of G3- ρ DTQW with SPPDs is given. In Section 3, we study properties of the model. Finally, a short discussion and conclusion is given in Section 4.

2 G3- ρ DTQW with SPPDs

Let’s start with a brief review of G3- ρ DTQW. The whole Hilbert space of the model is depicted as \(\mathcal {H}=\mathcal {H}_{\text {p}}\otimes \mathcal {H}_{\text {c}}\). Here, one orthogonal basis of a three-dimensional coin space \(\mathcal {H}_{\text {c}}\) is {|0〉,|1〉,|2〉}, where these three coin states represent left, stay, and right, respectively. The space \(\mathcal {H}_{\text {p}}\) denotes a so-called position space spanned by orthogonal position vectors \(\{|x\rangle |x\in \mathbb {Z}\}\), where \(\mathbb {Z}\) denotes a set of integers. So, the basis states of the whole quantum system are \(\{|x,c\rangle |x\in \mathbb {Z},c=0,1,2\}\). Thus, the generic state of quantum system at time t can be written as

$$\begin{array}{@{}rcl@{}} |\psi(t)\rangle = \sum\limits_{x=-\infty}^{+\infty}(\alpha_{x}(t)|x,0\rangle + \beta_{x}(t)|x,1\rangle + \gamma_{x}(t)|x,2\rangle), \end{array} $$
(1)

where, the probability amplitude α x (t), β x (t), and γ x (t) are complex functions. So, the probability of finding the walker at the position x at time t is expressed as follows,

$$\begin{array}{@{}rcl@{}} p_{x}(t) = |\alpha_{x}(t)|^{2} + |\beta_{x}(t)|^{2} + |\gamma_{x}(t)|^{2}, \end{array} $$
(2)

satisfying \(\sum \limits _{x=-\infty }^{+\infty } p_{x}(t) =1\).

The time evolution of the system at each step is defined by

$$\begin{array}{@{}rcl@{}} U_{\rho}=\left( \sum\limits_{c=0,1,2}|c\rangle\langle c|\otimes S_{c}\right)(C(\rho)\otimes I), \end{array} $$
(3)

where, S c is a shift operator given by S c |x〉=|x + c−1〉. C(ρ) is a coin operator defined by

$$ C(\rho) = \left( \begin{array}{ccc} -\rho^{2} & \rho\sqrt{2-2\rho^{2}} & 1-\rho^{2} \\ \rho\sqrt{2-2\rho^{2}} & 2\rho^{2}-1 & \rho\sqrt{2-2\rho^{2}} \\ 1-\rho^{2} & \rho\sqrt{2-2\rho^{2}} & -\rho^{2} \end{array} \right), $$
(4)

with the coin parameter ρ ∈ (0, 1).

Given a initial state |ψ(0)〉, we apply the operator U to the system t times successively, then the final state of the system is

$$\begin{array}{@{}rcl@{}} |\psi(t)\rangle &=& U^{t} |\psi(0)\rangle. \end{array} $$
(5)

Generally speaking, the walker starts from the origin, i.e. x = 0. In this paper, we also take the same assumption. So, the initial state is depicted as

$$ |\psi(0)\rangle =|0\rangle\otimes|\psi_{c}(0)\rangle, $$
(6)

where |ψ c (0)〉 is the initial coin state. It has shown that the choice of the initial coin state affects some features of the quantum walk model. More recently, in order to unveil unknown features which are hidden in the standard basis description, a suitable basis given by the eigenstates of the coin operator can be used as the initial coin state [27, 40]. So, the same initial coin state is also employed in this paper.

Now, we consider a modified quantum walk with SPPDs. In this model, the walker will gain an extra phase e iϕ at any designated position at each step, which can be achieved by replacing S c with S c (ϕ). This new shift operator is

$$ S_{c}(\phi)|x\rangle=e^{i\phi\delta_{x,n}}|x+c-1\rangle, $$
(7)

where n is a designated position, ϕ ∈ (0, 2π) and δ x, n is the Kronecker delta. Thus, the evolution operation of this model is changed to

$$\begin{array}{@{}rcl@{}} U_{\rho,\phi}=\left( \sum\limits_{c}|c\rangle\langle c|\otimes S_{c}(\phi)\right)(C(\rho)\otimes I). \end{array} $$
(8)

In order to investigate properties of QW model, another two physical quantities are used generally. One is the time-averaged probability at the origin given by

$$\begin{array}{@{}rcl@{}} \bar{p}_{0}(t) =\frac{1}{T}\sum\limits_{t=0}^{T-1}p_{0}(t). \end{array} $$
(9)

The quantum walk model exists localization effect, if the limit value of \(\bar {p}_{0}(t)\) is a positive value [22].

The other physical quantity is the position standard deviation σ(t) of the position probability distribution. It can be calculated by

$$\begin{array}{@{}rcl@{}} \sigma(t)= \sqrt{\langle x^{2}\rangle_{t} - \langle x{\rangle_{t}^{2}}}, \end{array} $$
(10)

where \(\langle x\rangle _{t}={\sum }_{x} xp_{x}(t),\langle x^{2}\rangle _{t}={\sum }_{x} x^{2}p_{x}(t)\). The slope of σ(t) is used to quantify the spreading rate of the walker.

3 Results

Before studying the properties of G3- ρ DTQW with SPPDs, we need to choose a suitable initial coin state. We utilize the eigenstates of the coin operator to construct the initial coin state. The eigenvectors of the coin operator C(ρ) [27] take the following forms

$$\begin{array}{@{}rcl@{}} |\sigma^{+}\rangle & = & \sqrt{\frac{1 - \rho^{2}}{2}}|0\rangle +\rho|1\rangle + \sqrt{\frac{1 - \rho^{2}}{2}}|2\rangle,\\[-2pt] |\sigma_{1}^{-}\rangle & = & \frac{\rho}{\sqrt{2}}|0\rangle -\sqrt{1-\rho^{2}}|1\rangle + \frac{\rho}{\sqrt{2}}|2\rangle, \\[-2pt] |\sigma_{2}^{-}\rangle & = & \frac{1}{\sqrt{2}}(|0\rangle - |2\rangle). \end{array} $$
(11)

Thus, the initial coin state is constructed in the form

$$ |\psi_{C}\rangle = g_{+}|\sigma^{+}\rangle + g_{1}|\sigma_{1}^{-}\rangle + g_{2}|\sigma_{2}^{-}\rangle, $$
(12)

with |g +|2 + |g 1|2 + |g 2|2 = 1.

In order to analyze this model in a sufficient way, we will consider two possible cases. The first is that the phase defect is added at n = 0 when the walker starts from the origin. The second case is that the phase defect is added at n ≠ 0 when the walker also starts from the origin.

Now we investigate G3- ρ DTQW with SPPDs at the origin for three initial coin states. At first, the eigenstate |σ +〉 is taken as the initial coin state. Without phase defect (ϕ = 0), there is a single peak at the origin, as shown in Fig. 1a. When the SPPD ϕ = π/8, the localized probability p 0(100) begins to increase, and both peaks on the edges appear [see Fig. 1b]. However, when ϕ = π/2, the localized probability decreases slightly and both peaks on the edges become quite apparent [see Fig. 1c]. When ϕ = π, both peaks on the edges grow small and the localized probability now is a larger value [see Fig. 1d].

Fig. 1
figure 1

The position probability distribution of the G3- ρ DTQW with the coin parameter ρ = 0.5 with SPPD ϕ at the origin after t = 100 steps. a without phase defect, b with SPPD ϕ = π/8, c ϕ = π/2, (d) ϕ = π. The initial coin state is |σ +〉

Full size image

In Fig. 2a, the position standard deviations of G3- ρ DTQW with SPPD ϕ = π at the origin are not much different from that of G3- ρ DTQW. However, when ϕ = π/8, π/2, the values of σ(t) are bigger than that of G3- ρ DTQW. That is, the walker spreads more quickly than that of G3- ρ DTQW. Figure 2b shows that the time-averaged probability at the origin rapidly goes to a constant, which indicates that the localization effect exists for the four values of ϕ. Moreover, the values of \(\bar {p}_{0}(100)\) are different for the four values of ϕ, which means that the degree of the localization is different. It is interesting to study that how to achieved to a strong localization effect. This model have only three parameters t, ρ, and ϕ. Here, we set t = 50 and study the dependence of the time-averaged probability at the origin on two parameters ρ and ϕ, as shown in Fig. 3a. It can been seen that the time-averaged probability is symmetrical about straight line ϕ = π.

Fig. 2
figure 2

a The position standard deviation of the G3- ρ DTQW with the coin parameter ρ = 0.5 with SPPD ϕ at the origin for t = 100 steps. b The time-averaged probability at the origin of the G3- ρ DTQW with the coin parameter ρ = 0.5 with SPPD ϕ at the origin for t = 100 steps. The initial coin state is |σ +〉

Full size image
Fig. 3
figure 3

a The time-averaged probability at the origin at t = 50 against the parameters ρ and ϕ of the G3- ρ DTQW with SPPD ϕ at the position n = 0. b The time-averaged probability at the origin at t = 50 against the parameters ϕ of the G3- ρ DTQW with SPPD ϕ at the position n = 0. We set ρ = 0.8. The initial coin state is |σ +〉

Full size image

To investigate this problem more clearly, the method proposed in Ref. [41] is utilized . In this method, we fix one parameter ρ (or ϕ) firstly. Then, we vary the value of the other parameter ϕ (or ρ) and obtain the corresponding time-average probability at the origin. Evidently, a certain number range of ϕ (or ρ) can be deduced on the condition that the time-average probability is greater than a threshold. That is to say, a strong localization is obtained. For instance, we can assume that ρ = 0.8 and t = 50, the result as shown in Fig. 3b. It can be seen that strong localization effect may be observed in the range ϕ ∈ [0, π/4]. By this way, the concrete values of two parameters ρ and ϕ can be calculated to achieve a strong localization effect in the presented quantum walk model.

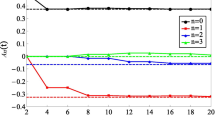
Second, we take the eigenstate \(|\sigma _{1}^{-}\rangle \) as the initial coin state. Without phase defect (ϕ = 0), only two peaks on the edges of the distribution exist, as shown in Fig. 4a. When ϕ = π/8, the peak at the origin appears and the height of both peaks on the edges decrease [see Fig. 4b]. The localized probability increases with the phase ϕ increasing from ϕ = π/8 to ϕ = π/2 [see Fig. 4c]. When ϕ = π, there is only a single peak at the origin [see Fig. 4d]. In Fig. 5a, the position standard deviations grow much smaller with the phase ϕ increasing from 0 to π, which means that the walker of G3- ρ DTQW with SPPDs at the origin spreads more slowly than that of G3- ρ DTQW. Figure 5b shows that the localization effect exists for the values of ϕ except ϕ = 0. The time-averaged probability at the origin as a function of two parameters ρ and ϕ for t = 50 steps is shown in Fig. 6, which is also symmetrical about straight line ϕ = π. A strong localization effect can be observed in the region surrounded by the yellow curve [see Fig. 6].

Fig. 4
figure 4

The position probability distribution of the G3- ρ DTQW with the coin parameter ρ = 0.5 with SPPD ϕ at the origin after t = 100 steps. a without phase defect, b with SPPD ϕ = π/8, c ϕ = π/2, d ϕ = π. The initial coin state is \(|\sigma _{1}^{-}\rangle \)

Full size image
Fig. 5
figure 5

a The position standard deviation of the G3- ρ DTQW with the coin parameter ρ = 0.5 with SPPD ϕ at the origin for t = 100 steps. b The time-averaged probability at the origin of the G3- ρ DTQW with the coin parameter ρ = 0.5 with SPPD ϕ at the origin for t = 100 steps. The initial coin state is \(|\sigma _{1}^{-}\rangle \)

Full size image
Fig. 6
figure 6

The time-averaged probability at the origin at t = 50 against the parameters ρ and ϕ of the G3- ρ DTQW with SPPD ϕ at the position n = 0. The initial coin state is \(|\sigma _{1}^{-}\rangle \)

Full size image

Finally, we take the eigenstate \(|\sigma _{2}^{-}\rangle \) as the initial coin state. Without phase defect (ϕ = 0), there are three peaks, as shown in Fig. 7a. Two are on the edges of the distribution and one is at the origin. When ϕ = π/8, the height of the three peaks decreases [see Fig. 7b]. When ϕ = π/2 and ϕ = π, the localization probability tends to 0, which means that the localization effect disappears. Moreover, both peaks on the edges of the distribution also tend to 0. The walker is trapped at the both positions x = ±1 with high probabilities [see Fig. 7c and d], which did not happen in the two-state case. The reason why this interesting phenomenon comes out is clearly related to the fact that the initial coin state \(|\sigma _{2}^{-}\rangle \) is a variation of the dark state for |1〉.

Fig. 7
figure 7

The position probability distribution of the G3- ρ DTQW with the coin parameter ρ = 0.5 with SPPD ϕ at the origin after t = 100 steps. a without phase defect, b with SPPD ϕ = π/8, c ϕ = π/2, d ϕ = π. The initial coin state is \(|\sigma _{2}^{-}\rangle \)

Full size image

Compared to the case without phase defect , the position standard deviations of the G3- ρ DTQW with the phase π/8 are not much changed. Whereas, the standard deviations of the G3- ρ DTQW with the phases π/2 or π grow much smaller, which is shown in Fig. 8a. Figure 8b shows that the localization effect exist for all the values of the phase ϕ. The time-averaged probability at the origin as a function of two parameters ρ and ϕ for a given t = 50 is shown in Fig. 9, which is also symmetrical about straight line ϕ = π. A strong localization effect can also be observed in the region surrounded by the yellow curve.

Fig. 8
figure 8

a The position standard deviation of the G3- ρ DTQW with the coin parameter ρ = 0.5 with SPPD ϕ at the origin for t = 100 steps. b The time-averaged probability at the origin of the G3- ρ DTQW with the coin parameter ρ = 0.5 with SPPD ϕ at the origin for t = 100 steps. The initial coin state is \(|\sigma _{1}^{-}\rangle \)

Full size image
Fig. 9
figure 9

The time-averaged probability at the origin at t = 50 against the parameters ρ and ϕ of the G3- ρ DTQW with SPPD ϕ at the position n = 0. The initial coin state is \(|\sigma _{1}^{-}\rangle \)

Full size image

In the above, the SPPD ϕ is added at the origin. It is interesting to study the localization effect if the SPPD ϕ is added at any other position. So, we set ρ = 0.5, t = 100, ϕ = π/2 and study the position probability distribution for different designated positions n = 1, 2, 5, 10, as shown in Figs. 10, 11 and 12. Some important features to note: (1) when x = 1, the walker localizes at x = 1 for the three initial coin state, however, the walker not localizes at x when x ≥ 2, which is similar to the conclusion in the two-state model [35]; (2) when x ≥ 2, localization at the origin can be still observed for the initial coin state |σ +〉 and \(|\sigma _{2}^{-}\rangle \), which did not happen in the two-state case [33]; (3) for the initial coin state \(|\sigma _{1}^{-}\rangle \), similarly to the two-state case [33], scattering effects can be observed.

Fig. 10
figure 10

The position probability distribution of the G3- ρ DTQW with the coin parameter ρ = 0.5 with SPPD ϕ = π/2 at at different positions after t = 100 steps. a n = 1, (b) n = 2, (c) n = 5, (d) n = 10. The initial coin state is |σ +〉

Full size image
Fig. 11
figure 11

The position probability distribution of the G3- ρ DTQW with the coin parameter ρ = 0.5 with SPPD ϕ = π/2 at at different positions after t = 100 steps. a n = 1, (b) n = 2, (c) n = 5, (d) n = 10. The initial coin state is \(|\sigma _{1}^{-}\rangle \)

Full size image
Fig. 12
figure 12

The position probability distribution of the G3- ρ DTQW with the coin parameter ρ = 0.5 with SPPD ϕ = π/2 at at different positions after t = 100 steps. a n = 1, (b) n = 2, (c) n = 5, (d) n = 10. The initial coin state is \(|\sigma _{2}^{-}\rangle \)

Full size image

4 Conclusion

Before giving a conclusion, we briefly introduce another quantum walk. In Ref. [23], besides G3- ρ DTQW, Stefaňák et al have presented another generalized Grove quantum walk, i.e., G3- φ DTQW. The corresponding coin operator is depicted as follows,

$$ C(\varphi) = \frac{1}{6}\left( \begin{array}{ccc} -1-e^{2i\varphi} & 2(1+e^{2i\varphi}) & 5-e^{2i\varphi} \\ 2(1+e^{2i\varphi}) & 2(1-2e^{2i\varphi}) & 2(1+e^{2i\varphi}) \\ 5-e^{2i\varphi} & 2(1+e^{2i\varphi}) & -1-e^{2i\varphi} \end{array} \right), $$
(13)

with the coin parameter \(\varphi \in (0,\frac {\pi }{2})\). In the same way, we are also able to propose the G3- φ DTQW with SPPDs. Similarly, the eigenstates of the coin operator are utilized to construct the initial coin state. Therefore, the eigenvectors of the coin operator C(φ) [27] are in the following forms,

$$\begin{array}{@{}rcl@{}} |\gamma^{+}\rangle & = & \frac{1}{\sqrt{3}}\left( |0\rangle + |1\rangle + |2\rangle\right), \\[-2pt] |\gamma_{1}^{-}\rangle & = & \frac{1}{\sqrt{6}}\left( |0\rangle - 2|1\rangle + |2\rangle \right),\\[-2pt] |\gamma_{2}^{-}\rangle & = & \frac{1}{\sqrt{2}}\left( |0\rangle - |2\rangle\right). \end{array} $$

The properties of this quantum walk are investigated by performing numerical simulation on classical computer. We take the eigenvector |γ +〉 as a initial coin state for example. The simulation results are shown in Figs. 13, 14 and 15. Obviously, this quantum walk has the similar properties to the G3- ρ DTQW with SPPDs. The main difference exists in the time-averaged probability. In the G3- φ DTQW with SPPDs, it is not symmetrical, as shown in Fig. 15.

Fig. 13
figure 13

The position probability distribution of the G3- ρ DTQW with the coin parameter φ = π/6 with SPPD ϕ at the origin after t = 100 steps. a without phase defect, (b) with SPPD ϕ = π/8, (c) ϕ = π/2, (d) ϕ = π. The initial coin state is |γ +〉

Full size image
Fig. 14
figure 14

a The position standard deviation of the G3- ρ DTQW with the coin parameter φ = π/6 with SPPD ϕ at the origin for t = 100 steps. b The time-averaged probability at the origin of the G3- ρ DTQW with the coin parameter φ = π/6with SPPD ϕ at the origin for t = 100 steps. The initial coin state is |γ +〉

Full size image
Fig. 15
figure 15

The time-averaged probability at the origin at t = 50 against the parameters ρ and ϕ of the G3- ρ DTQW with SPPD ϕ at the position n = 0. The initial coin state is |γ +〉

Full size image

We have studied a family of three-state quantum walks with SPPDs. Here, three eigenstates of the coin operator are considered as the initial coin states. It is shown that three characteristic peaks of the distribution for a special coin state are able to be controlled by varying the position and strength of the phase defect. Especially, we find that the initial coin state \(|\sigma _{2}^{-}\rangle \) may be a variation of the dark state for |1〉, which is not found in other quantum walks. Moreover, it is shown that the degree of localization effect can also be governed by the coin parameter, initial state and the phase defect’s position and strength. Compared with G3 DTQWs without SPPD, the proposed model can obtain larger maximal value of \(\bar {p}_{0}(t)\), which indicates that a stronger localization effect can be observed. Obviously, these conclusions may widen some possible applications of the model.