1 Introduction

Quantum game theory is an interdisciplinary field that combines quantum theory and game theory. The first attempt to describe a game in the quantum domain applied to a simple coin tossing game [1] and 2 × 2 bimatrix games [2, 3]. Shortly after that quantum game theory has found applications in various fields including decision sciences [4,5,6], financial theory [7,8,9] or mathematical psychology [5]. One of the economic applications concerns duopoly problems. First attempts at exploring quantum game theory to this field were made in [10, 11]. Iqbal and Toor’s scheme was further investigated, for example, in [12,13,14,15,16], Li, Du and Massar’s scheme in [17,18,19,20,21].

The Li-Du-Massar scheme appears to be a generally accepted quantum scheme for duopoly examples. It provides a “minimal” quantum structure of a two-player strategic-form game with a continuum of strategies. The scheme, originally designed for Cournot duopoly, enables the players to avoid an inefficient Nash equilibrium by means of quantum resources. Moreover, it preserves the uniqueness of the solution [10, 22]. In essence, the result has been proved for a specific Cournot duopoly example. Thus, the natural question arises whether the uniqueness of Nash equilibrium and its efficiency (Pareto optimality) hold in a more general setting. A natural generalization of the classically played Cournot duopoly is due to [23] (see also [24]), where the payoff functions of the players are assumed to depend on the demand and cost functions. Then suitable requirements on the payoff functions such as concavity of the demand function and convexity of the cost function imply a unique Nash equilibrium. This work is intended to generalize the above-mentioned fact to the game played according to the Li-Du-Massar model.

Our presentation is self-contained, and designed to be accessible without a background in game theory and quantum theory. The work starts with the important preliminaries from game theory. We also provide the reader with the idea of quantum game introduced in [10]. In Section 4 our main results are stated and proved.

2 Preliminaries on Game Theory

For completeness of exposition, we recall some of the standards facts on game theory that will be needed throughout the paper.

The basic object studied in game theory is a game in strategic form [25].

Definition 1

A game in strategic form is a triple (N,(S i ) i∈N ,(u i ) i∈N ) in which

  • N = {1,2,…, n} is the set of players,

  • S i is the set of strategies of player i, for each player i ∈ N,

  • \(u_{i}\colon S_{1}\times {\dots } \times S_{n} \to \mathbb {R}\) is a function associating each vector of strategies s = (s i ) i∈N with the payoff u i (s) to player i, for each player i ∈ N.

Cournot duopoly problem is one of the earliest economic models of competition between two players [26]. Player 1 and 2 offer quantities q 1 and q 2 of a homogeneous product and compete for the same market of potential buyers. The price of the product is a decreasing function that depends on the total quantity q = q 1 + q 2. Based on [27], the Cournot duopoly example can be viewed as a strategic form game (N,(S i ) i∈N ,(u i ) i∈N ) with the components defined as follows:

  1. 1.

    the set of players is N = {1,2},

  2. 2.

    player i’s strategy set is S i = [0, ∞) with typical element q i ,

  3. 3.

    player i’s payoff function u i is given by formula

    $$ u_{i}(q_{1}, q_{2}) = q_{i}P(q_{1},q_{2}) - cq_{i}, ~q_{1},q_{2} \in [0,\infty), $$
    (1)

    where P(q 1, q 2) represents the price of the product,

    $$ P(q_{1},q_{2}) = \left\{\begin{array}{ll} a-q_{1}-q_{2} &\text{if}~q_{1}+q_{2}<a,\\ 0 &\text{if}~q_{1}+q_{2} \geq a, \end{array}\right. $$
    (2)

    and c is a marginal cost such that a > c > 0.

Nash equilibrium is a fundamental solution concept of strategic-form games. It is a way of predicting reasonable results of the game, in particular, the result of the Cournot duopoly example. A Nash equilibrium is a strategy vector at which each strategy is a best reply to the other strategies [25].

Definition 2

A strategy vector \(s^{*}=(s^{*}_{1}, \dots , s^{*}_{n})\) is a Nash equilibrium if for each player i ∈ N and each strategy s i ∈ S i the following is satisfied:

$$ u_{i}(s^{*}) \geq u_{i}(s_{i}, s^{*}_{-i}). $$
(3)

The Cournot competition defined by (1) and (2) has the unique Nash equilibrium \((q^{*}_{1}, q^{*}_{2}) = ((a-c)/3, (a-c)/3)\). The existence of the Nash equilibrium is due to concavity of the payoff functions. In general, the following theorem can be proved [28].

Theorem 1

Let X 1 and X 2 be two compact convex sets in \(\mathbb {R}^{m}\) and \(\mathbb {R}^{n}\), respectively. Let u 1(x 1, x 2) and u 2(x 1, x 2) be two continuous functions on X 1 × X 2 such that u 1(x 1, x 2) is concave in x 1 for fixed x 2, and u 2(x 1, x 2) is concave in x 2 for fixed x 1. Then there exists a Nash equilibrium \((x^{*}_{1}, x^{*}_{2})\).

One can check (see, for example [27]) that the Nash equilibrium in the Cournot competition is not efficient. The players can benefit from playing strategy profile (q 1, q 2) = ((a − c)/4,(a − c)/4)). In other words, the Nash equilibrium \((q^{*}_{1}, q^{*}_{2})=((a-c)/3, (a-c)/3))\) is not Pareto-optimal.

Definition 3

Given a collection of payoff functions

$$ (u_{1}(x_{1}, \dots, x_{n}), \dots, u_{n}(x_{1}, \dots, x_{n})) $$
(4)

for an n-person nonzero sum game, we say that a strategy profile \((x^{*}_{1}, \dots , x^{*}_{n})\) is Pareto-optimal if there is no strategy profile \((x^{\prime }_{1}, \dots , x^{\prime }_{n})\) such that

$$ u_{i}(x^{\prime}_{1}, \dots, x^{\prime}_{n}) \geq u_{i}(x^{*}_{1}, \dots, x^{*}_{n}) $$
(5)

for i ∈{1,…, n} and

$$ u_{i}(x^{\prime}_{1}, \dots, x^{\prime}_{n}) > u_{i}(x^{*}_{1}, \dots, x^{*}_{n}) $$
(6)

for at least one i.

3 The Li-Du-Massar Quantum Duopoly Scheme

Let us recall the key elements of the Li-Du-Massar approach to duopoly examples [10] (see [29] for more details). Let |00〉 be the initial state and \(J(\gamma ) = e^{-\gamma (a^{\dag }_{1}a^{\dag }_{2} - a_{1}a_{2})}\) be a unitary operator, where γ ≥ 0 and \(a^{\dag }_{i}\) (a i ) represents the creation (annihilation) operator of electromagnetic field i. The player i’s strategies are unitary operators of the form

$$ D_{i}(x_{i}) = e^{x_{i}(a^{\dag}_{i} - a_{i})/ \sqrt{2}}, x_{i} \in [0,\infty), i = 1,2. $$
(7)

Then the operator J(γ) and the strategy profile D 1(x 1) ⊗ D 2(x 2) determine the final state |Ψf〉,

$$ |{\Psi}_{\mathrm{f}}\rangle = J^{\dag}(\gamma)(D_{1}(x_{1})\otimes D_{2}(x_{2}))J(\gamma)|00\rangle. $$
(8)

The quantity q i (or the price p i in the case of Bertrand duopoly examples) is then obtained by performing the measurement \(X_{i} = \left (a^{\dag }_{i} + a_{i}\right )/\sqrt {2}\) on the state |Ψf〉. The result is

$$ \begin{array}{l} q_{1} = \langle {\Psi}_{\mathrm{f}} | X_{1} |{\Psi}_{\mathrm{f}}\rangle = x_{1}\cosh{\gamma} + x_{2}\sinh{\gamma},\\ q_{2} = \langle {\Psi}_{\mathrm{f}} | X_{2} |{\Psi}_{\mathrm{f}}\rangle = x_{2}\cosh{\gamma} + x_{1}\sinh{\gamma}. \end{array} $$
(9)

We obtain the quantum extension of the classical Cournot duopoly by substituting (9) into (1),

$$ u_{1(2)}(x_{1}, x_{2}, \gamma) = \left\{\begin{array}{ll}q_{1(2)}(a-c-e^{\gamma}(x_{1} + x_{2})) &\text{if}~e^{\gamma}(x_{1} + x_{2}) < a,\\ -cq_{1(2)} &\text{if}~e^{\gamma}(x_{1} + x_{2}) \geq a. \end{array}\right. $$
(10)

We see from (7) that player i’s strategies can be identified with choosing x i ∈ [0, ∞). Furthermore, (9) shows that the scheme correlates the players’ strategies, and the higher the value of γ, the stronger correlation between x 1 and x 2.

It is worth pointing out that the resulting outputs (9) are not in units of x i ’s. Given x 1 and x 2 fixed, we see at once that q i increases with γ, for i = 1,2.

For convenience, we normalize (9). It can be done by setting

$$ x_{i} \mapsto D\left( \frac{x_{i}}{e^{\gamma}}\right). $$
(11)

It follows easily from (11) that the resulting quantities become

$$ q^{\prime}_{1} = \frac{x_{1}\cosh\gamma + x_{2}\sinh\gamma}{e^{\gamma}}, \quad q^{\prime}_{2} = \frac{x_{2}\cosh\gamma + x_{1}\sinh\gamma}{e^{\gamma}}. $$
(12)

Both ways of describing the correlation of x 1 and x 2 are equivalent when studying the Cournot duopoly by means of the Li-Du-Massar scheme. One can check that substituting (12) into (1) results in the unique Nash equilibrium \((x^{*}_{1}, x^{*}_{2})\) such that

$$ x^{*}_{1} = x^{*}_{2} = \frac{a-c}{3 + \tanh\gamma}. $$
(13)

In the case of (9) the Nash equilibrium strategy is

$$ x^{*}_{i} = \frac{(a-c)\cosh\gamma}{1 + 2e^{2\gamma}}, $$
(14)

which is simply the division of (13) by e γ. Using (12) is more convenient, for example, for comparing the classical and quantum equilibria. Note that strategy (13) ranges from the classical equilibrium strategy (a − c)/3 to strategy (a − c)/4 being part of the Pareto-optimal profile.

4 Quantum Approach to Generalized Cournot Duopoly

The generalization of the Cournot duopoly, as presented in [24], assumes that the price P(q 1, q 2) of the product is a function of the demand D(q) that depends on the total quantity q = q 1 + q 2. The cost function C(q i ) returns the cost of producing q i units of the good. As a result, player i’s payoff function is of the form

$$ u_{i}(q_{1}, q_{2}) = q_{i}D(q_{1} + q_{2}) -C(q_{i}). $$
(15)

We now determine the payoff functions u i according to the Li-Du-Massar approach. It is easily seen that the normalized quantities (12) satisfy equation q 1 + q 2 = x 1 + x 2. By substituting (12) into (15) we obtain

$$ \begin{array}{l} u_{1}(x_{1}, x_{2}, \gamma) = \frac{x_{1}\cosh\gamma + x_{2}\sinh\gamma}{e^{\gamma}}D(x_{1} +x_{2}) - C\left( \frac{x_{1}\cosh\gamma + x_{2}\sinh\gamma}{e^{\gamma}}\right),\\ u_{2}(x_{1}, x_{2}, \gamma) = \frac{x_{2}\cosh\gamma + x_{1}\sinh\gamma}{e^{\gamma}}D(x_{1} +x_{2}) - C\left( \frac{x_{2}\cosh\gamma + x_{1}\sinh\gamma}{e^{\gamma}}\right), \end{array} $$
(16)

for x 1, x 2 ≥ 0. As the following states, the payoff functions (16) determine the game with a unique Nash equilibrium under some further restrictions on D and C.

Proposition 1

Suppose that the demand function D(x 1 + x 2) is a continuous, strictly decreasing, concave function in the interval 0 ≤ x 1 + x 2 ≤ a, twice-differentiable in 0 < x 1 + x 2 < a that satisfies

$$ D(0) >0, \quad D(x_{1} + x_{2}) = 0, x_{1}+x_{2} \geq a. $$
(17)

Let the cost function C(x i ) be a strictly increasing, twice-differentiable, non-negative convex function with

$$ \frac{dC(0)}{dx_{i}}< D(0). $$
(18)

Then, the game defined by (16) has exactly one Nash equilibrium given by (x ∗, x ∗). The Nash equilibrium strategy is determined by the unique solution of the equation

$$ D(2x) + \frac{(1+\tanh\gamma)x}{2}\frac{dD(2x)}{dx} - \frac{dC(x)}{dx}= 0 $$
(19)

in the interval 0 < x < a.

Proof

Note that under the above assumptions,

$$\begin{array}{@{}rcl@{}} \frac{\partial^{2} u_{1(2)}(x_{1}, x_{2}, \gamma)}{\partial x^{2}_{1(2)}} &=& \frac{2\cosh\gamma}{e^{\gamma}}\frac{\partial D(x_{1} + x_{2})}{\partial x_{1(2)}}\\ &&+ \frac{x_{1(2)}\cosh\gamma + x_{2(1)}\sinh\gamma}{e^{\gamma}}\frac{\partial^{2}D(x_{1}+x_{2})}{\partial x^{2}_{1(2)}}\\ &&-\frac{\partial^{2}C\left( \frac{x_{1(2)}\cosh\gamma+x_{2(1)}\sinh\gamma}{e^{\gamma}}\right)}{\partial x_{1(2)}^{2}}<0. \end{array} $$
(20)

Hence, u i for i = 1,2 is strictly concave in x i , and by Theorem 1, there exists a Nash equilibrium in the strategic-form game ({1,2},{[0, ∞),[0, ∞)},{u 1, u 2}). We first prove that there is no Nash equilibrium (x1∗, x2∗) for which \(x^{*}_{1} + x^{*}_{2} \geq a\). According to the assumptions on D(x 1 + x 2), in that case,

$$ u_{1(2)}(x_{1}, x_{2}, \gamma) = -C\left( \frac{x_{1(2)}\cosh\gamma + x_{2(1)}\sinh\gamma}{e^{\gamma}}\right). $$
(21)

Since − C((x 1(2) coshγ + x 2(1) sinhγ)/e γ) < 0 for x 1 + x 2 ≥ a and γ ≥ 0, and C is strictly increasing, player i is better off choosing x i = 0 rather than \(x^{*}_{i}\ne 0\). Furthermore, it cannot be the case that \((x^{*}_{1}, x^{*}_{2}) = (0,0)\). Indeed, ∂u 1(x 1, x 2, γ)/∂x 1 is continuous with respect to x 1 and

$$ \frac{\partial u_{1}(0,0, \gamma)}{\partial x_{1}} = \frac{\cosh\gamma}{e^{\gamma}}D(0) - \frac{\partial C(0)}{\partial x_{1}} >0. $$
(22)

By the sign-preserving property, ∂u 1(x 1,0, γ)/∂x 1 > 0 in a nonempty interval (0, ε). It follows that u 1(x 1,0, γ) is strictly increasing in (0, ε). Hence player 1 gains from switching from strategy x 1 = 0 to x 1 > 0.

Let us assume that \(x^{*}_{i} > 0\) for i = 1,2. Since \(x^{*}_{1}\) is an Nash equilibrium strategy, the payoff function \(u_{1}(x_{1}, x^{*}_{2}, \gamma )\) attains its maximum at \(x_{1} = x^{*}_{1}\). This gives

$$\begin{array}{@{}rcl@{}} \frac{\partial u_{1}(x^{*}_{1}, x^{*}_{2}, \gamma)}{\partial x_{1}} &=& \frac{\cosh\gamma}{e^{\gamma}}D(x^{*}_{1} + x^{*}_{2}) + \frac{x^{*}_{1}\cosh\gamma + x^{*}_{2}\sinh\gamma}{e^{\gamma}}\frac{\partial D(x^{*}_{1} + x^{*}_{2})}{\partial x_{1}} \\&&- \frac{\partial C\left( \frac{x^{*}_{1}\cosh\gamma + x^{*}_{2}\sinh\gamma}{e^{\gamma}}\right)}{\partial x_{1}} = 0 \end{array} $$
(23)

and

$$\begin{array}{@{}rcl@{}} \frac{\partial u_{2}(x^{*}_{1}, x^{*}_{2}, \gamma)}{\partial x_{2}} &=& \frac{\cosh\gamma}{e^{\gamma}}D(x^{*}_{1} + x^{*}_{2}) + \frac{x^{*}_{2}\cosh\gamma + x^{*}_{1}\sinh\gamma}{e^{\gamma}}\frac{\partial D(x^{*}_{1} + x^{*}_{2})}{\partial x_{2}}\\ &&- \frac{\partial C\left( \frac{x^{*}_{2}\cosh\gamma + x^{*}_{1}\sinh\gamma}{e^{\gamma}}\right)}{\partial x_{2}} = 0. \end{array} $$
(24)

By assumption, the demand function D depends merely on x 1 + x 2. This clearly forces

$$ \frac{\partial D(x_{1} + x_{2})}{\partial x_{1}} = \frac{\partial D(x_{1} + x_{2})}{\partial x_{2}}. $$
(25)

Subtracting (23) from (24) yields

$$\begin{array}{@{}rcl@{}} &&\frac{x^{*}_{1}-x^{*}_{2}}{e^{2\gamma}}\frac{\partial D(x^{*}_{1} + x^{*}_{2})}{\partial x_{1}}-\left( \frac{\partial C\left( \frac{x^{*}_{1}\cosh\gamma + x^{*}_{2}\sinh\gamma}{e^{\gamma}}\right)}{\partial x_{1}} - \frac{\partial C\left( \frac{x^{*}_{2}\cosh\gamma + x^{*}_{1}\sinh\gamma}{e^{\gamma}}\right)}{\partial x_{2}}\right) = 0.\\ \end{array} $$
(26)

Suppose, contrary to our claim, that \(x^{*}_{1} > x^{*}_{2}\). Since C is convex, the derivatives ∂C/∂x i for i = 1,2 are increasing. Moreover ∂D(x 1 + x 2)/∂x 1 < 0 for x 1 + x 2≠ 0. Using the fact that inequality x 1 > x 2 is equivalent to

$$ (x_{1}\cosh\gamma + x_{2}\sinh\gamma)e^{-\gamma} > (x_{2}\cosh\gamma + x_{1}\sinh\gamma)e^{-\gamma} $$
(27)

for all γ ∈ [0, ∞), we conclude that the left-hand side of (26) is negative. So it must be the case that \(x^{*}_{1} \leq x^{*}_{2}\). However, by a similar argument, \((x^{*}_{1}, x^{*}_{2})\) with \(x^{*}_{1} < x^{*}_{2}\) does not satisfy (26). We thus get \(x^{*}_{1} = x^{*}_{2} = x^{*}\). Note that by the chain rule,

$$ \frac{\partial D(x_{1} + x_{2})}{\partial x_{1}} = \frac{d D(x_{1} + x_{2})}{d (x_{1} + x_{2})} $$
(28)

and

$$ \frac{\partial C\left( \frac{x_{1}\cosh\gamma + x_{2}\sinh\gamma}{e^{\gamma}} \right)}{\partial x_{1}} = \frac{\cosh\gamma}{e^{\gamma}}\frac{dC\left( \frac{x_{1}\cosh\gamma + x_{2}\sinh\gamma}{e^{\gamma}} \right)}{d\left( \frac{x_{1}\cosh\gamma + x_{2}\sinh\gamma}{e^{\gamma}}\right)}. $$
(29)

Since we can restrict our attention to x 1 = x 2 = x, the derivatives (28) and (29) in this case can be written as

$$\begin{array}{@{}rcl@{}} \frac{\partial D(x_{1} + x_{2})}{\partial x_{1}} &=& \frac{dD(2x)}{d(2x)} = \frac{1}{2}\frac{dD(2x)}{dx},\\ \frac{\partial C\left( \frac{x_{1}\cosh\gamma + x_{2}\sinh\gamma}{e^{\gamma}} \right)}{\partial x_{1}} &=& \frac{\cosh\gamma}{e^{\gamma}}\frac{dC(x)}{dx}. \end{array} $$
(30)

Taking into account (30) we can simplify (23) and (24) to

$$ \frac{\cosh\gamma}{e^{\gamma}}\left( D(2x) - \frac{dC(x)}{dx}\right) + \frac{x}{2}\frac{dD(2x)}{dx} = 0 $$
(31)

which is equivalent to (19).

The proof is completed by showing that the equilibrium strategy x ∗ is a unique root of (19). Denote by h(x) the left hand-side of (19). Then, by assumption,

$$ h(0) = D(0) - \frac{dC(0)}{dx}> 0. $$
(32)

Since D is continuous, D(a) = 0, and it has a negative and decreasing derivative, for y ∈ (0, a/2) sufficiently close to a/2

$$ h\left( y\right) \approx \frac{(1+\tanh\gamma)y}{2}\frac{dD(2y)}{dx} -\frac{dC(y)}{dx} <0. $$
(33)

Direct consideration of dh(x)/dx shows that h(x) is strictly decreasing in 0 < x < a/2. Hence h(x) has a unique root in 0 < x < a/2. This finishes the proof. □

Remark 1

Proposition 1 becomes a reformulation of Theorem 7.2.4 (see [24]) in case γ = 0. According to that theorem, Nash equilibrium strategy is supposed to be the unique solution of the equation

$$ D(2x) + xD^{\prime}(2x) - C^{\prime}(x)= 0. $$
(34)

if functions D and C satisfy similar assumptions to ones given in Proposition 1. In fact, (34) does not lead us to the Nash equilibrium as term D ′(2x) of (34) needs handling with greater care. Applying (34) to the Cournot duopoly example mentioned in the Preliminaries (see also Example 1 below) yields equation a − 4x − c = 0 whose the solution is part of the Pareto-optimal outcome. In order to avoid this issue we need to take the derivative of D(2x) with respect to 2x.

In what follows, we apply Proposition 1 to determine Nash equilibria in the quantum Cournot-type competition. The following example gives us a look at how (19) simplifies the analysis required to find Nash equilibria compared to [10, 22].

Example 1

Consider the classical Cournot duopoly example studied in [10, 22]. In that case,

$$ D(x_{1} + x_{2}) = \left\{\begin{array}{ll} a - (x_{1}+x_{2}) &\text{if}~x_{1}+x_{2} < a \\ 0 &\text{otherwise} \end{array}\right., \quad C(x_{i}) = cx_{i}, \;c>0. $$
(35)

Now (19) becomes

$$ a-2x -(1+\tanh\gamma)x -c = 0. $$
(36)

The above equation leads to the unique solution

$$ x^{*}(\gamma) = \frac{a-c}{3 + \tanh\gamma} \xrightarrow[\gamma \to \infty]{} \frac{a-c}{4}. $$
(37)

It is equivalent with the result obtained by means of the best response correspondences [22].

As the next example illustrates, Nash equilibria can be easily found also in case the demand function or the cost function are not linear.

Example 2

Let

$$ D(x_{1} + x_{2}) = \left\{\begin{array}{ll} a - (x_{1} + x_{2})^{2} &\text{if}~ x_{1} + x_{2} <a\\ 0 &\text{otherwise} \end{array}\right., \quad C(x_{i}) = \sqrt{a}x_{i}. $$
(38)

Equation (19) now reads

$$ a-2\sqrt{a} x - 4x^{2}(2 +\tanh\gamma)= 0 $$
(39)

yielding the unique positive solution

$$ x^{*}(\gamma) = \frac{\sqrt{a}}{1+\sqrt{9 + 4\tanh\gamma}}. $$
(40)

Having determined the Nash equilibrium in the game defined by (38) we are now in a position to compare the resulting payoffs for different values of γ. Focusing on strategy profiles in the form (x, x) we can use u i (x 1, x 2,0) to study the payoffs in both the classical and quantum game as we have u i (x, x,0) = u i (x, x, γ). A direct calculation shows that

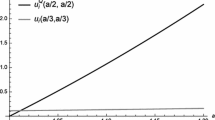
$$\begin{array}{@{}rcl@{}} u_{i}(x^{*}(0), x^{*}(0), 0) &=&\frac{\sqrt{a^{3}}}{8}< \frac{\sqrt{a^{3}}\left( 4\tanh\gamma + \sqrt{4\tanh\gamma + 9} + 5\right)}{\left( \sqrt{4\tanh\gamma + 9}+ 1\right)^{3}} \\ &=& u_{i}(x^{*}(\gamma), x^{*}(\gamma), 0) \end{array} $$
(41)

for γ ∈ (0, ∞). The value u i (x ∗(γ), x ∗(γ),0) converges to \(\sqrt {a^{3}}\left (13\sqrt {13} - 19\right )/216 \approx 0.129\sqrt {a^{3}}\) as γ increases to infinity (see, Fig. 1).

Fig. 1
figure 1

The values of payoff function u i in Example 2 for a = 1

Full size image

In the classical version of the Cournot problem presented in Example 1, the Nash equilibrium is not efficient. Both players could strictly benefit from playing ((a − c)/4,(a − c)/4)–the Pareto-optimal profile that is the limit of Nash equilibria in the Li-Du-Massar approach to the game as γ goes to infinity. The same applies to Example 2. The limit of the right-hand side of inequality (41) is the maximal payoff that both players can gain in the game. It turns out that this is a general result.

Proposition 2

Let (x ∗(γ), x ∗(γ)) be a Nash equilibrium in the Li-Du-Massar approach to the generalized Cournot duopoly. Then a strategy profile (x ∗, x ∗) such that \(x^{*} = \lim _{\gamma \to \infty }x^{*}(\gamma )\) is Pareto-optimal.

Proof

We obtain the Pareto-optimal profile in the classical Cournot duopoly by solving the following problem

$$ \operatornamewithlimits{arg\,max}_{x_{1}, x_{2} \geq 0}(u_{1}(x_{1}, x_{2}, 0) + u_{2}(x_{1}, x_{2}, 0)). $$
(42)

By the definition of u 1 and u 2 we have

$$ u_{1}(x_{1}, x_{2}, 0) + u_{2}(x_{1}, x_{2}, 0) = (x_{1} + x_{2})D(x_{1} + x_{2}) - (C(x_{1}) + C(x_{2})). $$
(43)

As C is convex, it follows that

$$ C(x_{1}) + C(x_{2}) \geq 2C\left( \frac{x_{1} + x_{2}}{2}\right). $$
(44)

Hence it is sufficient to consider

$$ \operatornamewithlimits{arg\,max}_{0 \leq x\leq a/2}(xD(2x) - C(x)) $$
(45)

in order to obtain a solution of (42). Write g(x) = xD(2x) − C(x). Then

$$ \frac{d^{2}g(x)}{dx^{2}} = 2\frac{dD(2x)}{dx} + x\frac{d^{2}D(2x)}{dx^{2}} - \frac{d^{2}C(x)}{dx^{2}} <0. $$
(46)

in the interval 0 < x < a/2. We conclude from (46) that g is strictly concave in 0 ≤ x ≤ a/2, and finally that a local maximum x ∗ of g is unique and global. Clearly

$$ \frac{dg(x^{*})}{dx} = D(2x^{*}) + x^{*}\frac{dD(2x^{*})}{dx} - \frac{dC(x^{*})}{dx} = 0. $$
(47)

Note that (47) is the limit of (19) as γ goes to infinity. We know from Proposition 1 that (19) gives a Nash equilibrium strategy in the quantum Cournot duopoly. Thus, (19) determines the Pareto-optimal equilibrium as γ approaches infinity. This is the desired conclusion. □

5 Conclusions

Studies on quantum game theory so far have given us a lot of information about how specific games can be described in the quantum domain. The work presented in this paper was an attempt to generalize some of the existing results rather than examine another game. Our research has shown that the results concerning a Cournot duopoly example can be extended to a wide class of games. In each case of the Cournot-type competition including nonlinear demand and cost functions, the Li-Du-Massar approach to the game implies the unique Nash equilibrium converging to the Pareto-optimal outcome as the entanglement measure goes to infinity. The equilibrium can be easily found by solving an equation that is of similar complexity than one in the classical case.