A combined experimental and modelling approach to aortic valve viscoelasticity in tensile deformation

Abstract

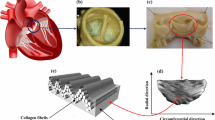
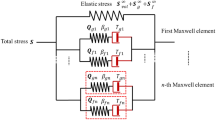
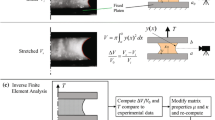
The quasi-static mechanical behaviour of the aortic valve (AV) is highly non-linear and anisotropic in nature and reflects the complex collagen fibre kinematics in response to applied loading. However, little is known about the viscoelastic behaviour of the AV. The aim of this study was to investigate porcine AV tissue under uniaxial tensile deformation, in order to establish the directional dependence of its viscoelastic behaviour. Rate dependency associated with different mechanical properties was investigated, and a new viscoelastic model incorporating rate effects developed, based on the Kelvin-Voigt model. Even at low applied loads, experimental results showed rate dependency in the stress–strain response, and also hysteresis and dissipation effects. Furthermore, corresponding values of each parameter depended on the loading direction. The model successfully predicted the experimental data and indicated a ‘shear-thinning’ behaviour. By extrapolating the experimental data to that at physiological strain rates, the model predicts viscous damping coefficients of 8.3 MPa s and 3.9 MPa s, in circumferential and radial directions, respectively. This implies that the native AV offers minimal resistance to internal shear forces induced by blood flow, a potentially critical design feature for substitute implants. These data suggest that the mechanical behaviour of the AV cannot be thoroughly characterised by elastic deformation and fibre recruitment assumptions alone.

Appendix 1

Let the variables (a ₁, a ₂, a ₃) identify a particle in the original configuration of the continuum, and (x ₁, x ₂, x ₃) be the coordinates of that particle when the body is deformed. The deformation of the body is known if (x ₁, x ₂, x ₃) is a known function of (a ₁, a ₂, a ₃) [29]:

$$ x_{i} = x_{i} \left( {a_{1} , a_{2} , a_{3} } \right),i = 1,2,3 $$

(11)

This could mathematically be considered as a transformation from a ₁, a ₂, a ₃ to x ₁, x ₂, x ₃. The transformation is one-to-one, such that is the functions in (11) are single-valued, continuous and have a unique inverse:

$$ a_{i} = a_{i} \left( {x_{1} ,x_{2} ,x_{3} } \right) $$

(12)

for every point in continuum [29].

Consider an infinitesimal line element connecting the point P(a ₁, a ₂, a ₃) to a neighbouring point P′(a ₁ + da ₁, a ₂ + da ₂, a ₃ + da ₃). The length of the line PP′ in the original configuration of the continuum will be:

$$ ds_{0}^{2} = da_{1}^{2} + da_{2}^{2} + da_{3}^{2} $$

(13)

When P and P′ are deformed to the points Q(x ₁, x ₂, x ₃) and Q′(x ₁ + dx ₁, x ₂ + dx ₂, x ₃ + dx ₃), respectively, the length ds of the new deformed QQ′ line is:

$$ ds^{2} = dx_{1}^{2} + dx_{2}^{2} + dx_{3}^{2} $$

(14)

From Eqs. 11 and 12 one can get:

$$ dx_{i} = {\frac{{\partial x_{i} }}{{\partial a_{j} }}}da_{j} ,\,da_{i} = {\frac{{\partial a_{i} }}{{\partial x_{j} }}}dx_{j} $$

(15)

Considering Eq. 15, Eqs. 13 and 14 can now be written as:

$$ ds_{0}^{2} = da_{i} da_{j} \delta_{ij} = {\frac{{\partial a_{i} }}{{\partial x_{l} }}} \cdot {\frac{{\partial a_{j} }}{{\partial x_{m} }}}dx_{l} dx_{m} \delta_{ij} $$

(16)

$$ ds^{2} = dx_{i} dx_{j} \delta_{ij} = {\frac{{\partial x_{i} }}{{\partial a_{l} }}} \cdot {\frac{{\partial x_{j} }}{{\partial a_{m} }}}da_{l} da_{m} \delta_{ij} $$

(17)

where δ _ij is the Kronecker delta. Now the following can be written:

$$ ds^{2} - ds_{0}^{2} = dx_{i} dx_{j} \delta_{ij} - da_{i} da_{j} \delta_{ij} = \left( {{\frac{{\partial x_{l} }}{{\partial a_{i} }}} \cdot {\frac{{\partial x_{k} }}{{\partial a_{j} }}} - \delta_{ij} } \right)da_{i} da_{j} $$

(18)

The Green strain tensor is defined by the term in parenthesis in the above equation as [29]:

$$ \varepsilon_{ij} = \frac{1}{2}\left( {{\frac{{\partial x_{l} }}{{\partial a_{i} }}} \cdot {\frac{{\partial x_{k} }}{{\partial a_{j} }}} - \delta_{ij} } \right) $$

(19)

Defining the extension ratios in the principle planar directions of 1 and 2 by λ ₁ and λ ₂, as the ratio of the final length of the element to its original length, we will have:

$$ \lambda_{1} = {\frac{{\partial x_{1} }}{{\partial a_{1} }}},\,\lambda_{2} = {\frac{{\partial x_{2} }}{{\partial a_{2} }}} $$

(20)

Now the components of the Green strain tensor in Eq. 19 for deformation in directions 1 and 2 can be written by the extension ratios in Eq. 20 as:

$$ \left\{ \begin{aligned} \varepsilon_{11} &= {\frac{{\left( {\lambda_{1}^{2} - 1} \right)}}{2}} \hfill \\ \varepsilon_{22} &= {\frac{{\left( {\lambda_{2}^{2} - 1} \right)}}{2}} \hfill \\ \varepsilon_{12} &= \varepsilon_{21} = 0 \hfill \\ \end{aligned} \right. $$

(21)

Taking the time derivative of Eq. 18 gives the rate of deformation tensor in terms of the time rate of Green strain tensor:

$$ \left[ {\left( {{\frac{{\partial v_{i} }}{{\partial x_{j} }}}} \right) + \left( {{\frac{{\partial v_{j} }}{{\partial x_{i} }}}} \right)} \right]dx_{i} dx_{j} = 2\dot{\varepsilon }_{ij} da_{i} da_{j} $$

(22)

where v _i is the ith component of the in-plane velocity field, x _i , and the rate of deformation tensor would be:

$$ V_{ij} = \frac{1}{2}\left[ {\left( {{\frac{{\partial v_{i} }}{{\partial x_{j} }}}} \right) + \left( {{\frac{{\partial v_{j} }}{{\partial x_{i} }}}} \right)} \right] $$

(23)

For an arbitrary choice of coordination component, and considering Eq. 22, the above equation becomes:

$$ V_{ij} = \dot{\varepsilon }_{kl} \left( {{\frac{{\partial a_{k} }}{{\partial x_{i} }}}} \right)\left( {{\frac{{\partial a_{l} }}{{\partial x_{j} }}}} \right) $$

(24)

From Eqs. 21 and 24, the components of the rate of deformation tensor in directions 1 and 2 can be obtained as:

$$ \left\{ \begin{aligned} V_{11} &= {\frac{{\dot{\lambda }_{1} }}{{\lambda_{1} }}} \hfill \\ V_{22} &= {\frac{{\dot{\lambda }_{2} }}{{\lambda_{2} }}} \hfill \\ V_{12} &= V_{21} = 0 \hfill \\ \end{aligned} \right. $$

(25)