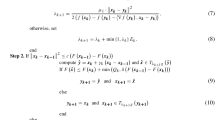Abstract
This paper proposes an inertial Bregman proximal gradient method for minimizing the sum of two possibly nonconvex functions. This method includes two different inertial steps and adopts the Bregman regularization in solving the subproblem. Under some general parameter constraints, we prove the subsequential convergence that each generated sequence converges to the stationary point of the considered problem. To overcome the parameter constraints, we further propose a nonmonotone line search strategy to make the parameter selections more flexible. The subsequential convergence of the proposed method with line search is established. When the line search is monotone, we prove the stronger global convergence and linear convergence rate under Kurdyka–Łojasiewicz framework. Moreover, numerical results on SCAD and MCP nonconvex penalty problems are reported to demonstrate the effectiveness and superiority of the proposed methods and line search strategy.




Similar content being viewed by others
References
Ahookhosh, M., Themelis, A., Patrinos, P.: A Bregman forward-backward linesearch algorithm for nonconvex composite optimization: superlinear convergence to nonisolated local minima (2019). arXiv:1905.11904
Alecsa, C.D., László, S.C., Pinţa, T.: An extension of the second order dynamical system that models Nesterov’s convex gradient method. Appl. Math. Optim. (2020). https://doi.org/10.1007/s00245-020-09692-1
Alvarez, F., Attouch, H.: An inertial proximal method for maximal monotone operators via discretization of a nonlinear oscillator with damping. Set Valued Anal. 9, 3–11 (2001)
Attouch, H., Bolte, J., Svaiter, B.F.: Convergence of descent methods for semi-algebraic and tame problems: proximal algorithms, forward–backward splitting, and regularized Gauss-Seidel methods. Math. Program. 137, 91–129 (2013)
Attouch, H., Peypouquet, J., Redont, P.: A dynamical approach to an inertial forward–backward algorithm for convex minimization. SIAM J. Optim. 24, 232–256 (2014)
Auslender, A., Teboulle, M.: Interior gradient and proximal methods for convex and conic optimization. SIAM J. Optim. 16, 697–725 (2006)
Auslender, A., Teboulle, M.: Projected subgradient methods with non-Euclidean distances for non-differentiable convex minimization and variational inequalities. Math. Program. 120, 27–48 (2009)
Bauschke, H.H., Bolte, J., Chen, J., Teboulle, M., Wang, X.: On linear convergence of non-Euclidean gradient methods without strong convexity and Lipschitz gradient continuity. J. Optim. Theory Appl. 182, 1068–1087 (2019)
Bauschke, H.H., Combettes, P.L.: Convex Analysis and Monotone Operator Theory in Hilbert Spaces. Springer, Berlin (2011)
Bauschke, H.H., Dao, M.N., Lindstrom, S.B.: Regularizing with Bregman–Moreau envelopes. SIAM J. Optim. 28, 3208–3228 (2018)
Beck, A., Teboulle, M.: A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2, 183–202 (2009)
Bertsekas, D.P.: Nonlinear Programming. Athena Scientific, Belmont (1999)
Bolte, J., Sabach, S., Teboulle, M.: Proximal alternating linearized minimization or nonconvex and nonsmooth problems. Math. Program. 146, 459–494 (2014)
Bolte, J., Sabach, S., Teboulle, M., Vaisbourd, Y.: First-order methods beyond convexity and Lipschitz gradient continuity with applications to quadratic inverse problems. SIAM J. Optim. 28, 2131–2151 (2018)
Boţ, R.I., Csetnek, E.R., László, S.C.: An inertial forward-backward algorithm for the minimization of the sum of two nonconvex functions. EURO J. Comput. Optim. 4, 3–25 (2016)
Cai, J.-F., Candès, E.J., Shen, Z.: A singular value thresholding algorithm for matrix completion. SIAM J. Optim. 20, 1956–1982 (2010)
Carmon, Y., Duchi, J.C., Hinder, O., Sidford, A.: Accelerated methods for nonconvex optimization. SIAM J. Optim. 28, 1751–1772 (2018)
Chen, C., Chan, R.H., Ma, S., Yang, J.: Inertial proximal ADMM for linearly constrained separable convex optimization. SIAM J. Imaging Sci. 8, 2239–2267 (2015)
Fan, J., Li, R.: Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 96, 1348–1360 (2001)
Gao, X., Cai, X., Han, D.: A Gauss-Seidel type inertial proximal alternating linearized minimization for a class of nonconvex optimization problems. J. Global Optim. 76, 863–887 (2020)
Ghadimi, S., Lan, G.: Accelerated gradient methods for nonconvex nonlinear and stochastic programming. Math. Program. 156, 59–99 (2016)
Ghayem, F., Sadeghi, M., Babaie-Zadeh, M., Chatterjee, S., Skoglund, M., Jutten, C.: Sparse signal recovery using iterative proximal projection. IEEE Trans. Signal Process. 66, 879–894 (2018)
Guo, K., Han, D.: A note on the Douglas–Rachford splitting method for optimization problems involving hypoconvex functions. J. Global Optim. 72, 431–441 (2018)
Han, D.: A generalized proximal-point-based prediction-correction method for variational inequality problems. J. Comput. Appl. Math. 221, 183–193 (2008)
Hien, L.T.K., Gillis, N., Patrinos, P.: Inertial block mirror descent method for non-convex non-smooth optimization (2019). arXiv:1903.01818
Hsieh, Y.-P., Kao, Y.-C., Mahabadi, R.K., Yurtsever, A., Kyrillidis, A., Cevher, V.: A non-Euclidean gradient descent framework for non-convex matrix factorization. IEEE Trans. Signal Process. 66, 5917–5926 (2018)
Jain, P., Kar, P.: Non-convex optimization for machine learning. Found. Trends Mach. Learn. 10, 142–336 (2017)
Johnstone, P.R., Moulin, P.: Local and global convergence of a general inertial proximal splitting scheme for minimizing composite functions. Comput. Optim. Appl. 67, 259–292 (2017)
Li, H., Lin, Z.: Accelerated proximal gradient methods for nonconvex programming. In: Proceedings of NeurIPS, pp. 379–387 (2015)
Liang, J., Monteiro, R.D., Sim, C.-K.: A FISTA-type accelerated gradient algorithm for solving smooth nonconvex composite optimization problems (2019). arXiv:1905.07010
Lorenz, D.A., Pock, T.: An inertial forward-backward algorithm for monotone inclusions. J. Math. Imaging Vis. 51, 311–325 (2015)
Lu, C., Tang, J., Yan, S., Lin, Z.: Nonconvex nonsmooth low rank minimization via iteratively reweighted nuclear norm. IEEE Trans. Image Process. 25, 829–839 (2016)
Lu, H., Freund, R.M., Nesterov, Y.: Relatively smooth convex optimization by first-order methods, and applications. SIAM J. Optim. 28, 333–354 (2018)
Moudafi, A., Oliny, M.: Convergence of a splitting inertial proximal method for monotone operators. J. Comput. Appl. Math. 155, 447–454 (2003)
Mukkamala, M.C., Ochs, P., Pock, T., Sabach, S.: Convex-concave backtracking for inertial Bregman proximal gradient algorithms in non-convex optimization (2019). arXiv:1904.03537
Nesterov, Y.: A method for solving the convex programming problem with convergence rate O(\(1/k^2\)). Soviet Math. Dok. 27, 372–376 (1983)
Nesterov, Y.: Gradient methods for minimizing composite functions. Math. Program. 140, 125–161 (2013)
Ochs, P., Chen, Y., Brox, T., Pock, T.: iPiano: inertial proximal algorithm for nonconvex optimization. SIAM J. Imaging Sci. 7, 1388–1419 (2014)
Ochs, P., Fadili, J., Brox, T.: Non-smooth non-convex Bregman minimization: unification and new algorithms. J. Optim. Theory Appl. 181, 244–278 (2019)
Osher, S., Burger, M., Goldfarb, D., Xu, J., Yin, W.: An iterative regularization method for total variation-based image restoration. Multiscale Model. Simul. 4, 460–489 (2005)
Pock, T., Sabach, S.: Inertial proximal alternating linearized minimization (iPALM) for nonconvex and nonsmooth problems. SIAM J. Imaging Sci. 9, 1756–1787 (2016)
Polyak, B.T.: Some methods of speeding up the convergence of iteration methods. USSR Comput. Math. Math. Phys. 4, 1–17 (1964)
Rockafellar, R.T., Wets, R.J.B.: Variational Analysis. Springer, Berlin (2009)
Teboulle, M.: A simplified view of first order methods for optimization. Math. Program. 170, 67–96 (2018)
Themelis, A., Stella, L., Patrinos, P.: Forward-backward envelope for the sum of two nonconvex functions: further properties and nonmonotone linesearch algorithms. SIAM J. Optim. 28, 2274–2303 (2018)
Wen, B., Chen, X., Pong, T.K.: Linear convergence of proximal gradient algorithm with extrapolation for a class of nonconvex nonsmooth minimization problems. SIAM J. Optim. 27, 124–145 (2017)
Wu, Z., Li, M.: General inertial proximal gradient method for a class of nonconvex nonsmooth optimization problems. Comput. Optim. Appl. 73, 129–158 (2019)
Wu, Z., Li, M., Wang, D.Z., Han, D.: A symmetric alternating direction method of multipliers for separable nonconvex minimization problems. Asia Pac. J. Oper. Res. 34(6), 1750030 (2017)
Yang, L.: Proximal gradient method with extrapolation and line search for a class of nonconvex and nonsmooth problems (2018). arXiv:1711.06831
Yin, W., Osher, S., Goldfarb, D., Darbon, J.: Bregman iterative algorithms for \(\ell _1\)-minimization with applications to compressed sensing. SIAM J. Imaging Sci. 1, 143–168 (2008)
Zhang, C.-H.: Nearly unbiased variable selection under minimax concave penalty. Ann. Stat. 38, 894–942 (2010)
Zhang, X., Barrio, R., Martínez, M.A., Jiang, H., Cheng, L.: Bregman proximal gradient algorithm with extrapolation for a class of nonconvex nonsmooth minimization problems. IEEE Access 7, 126515–126529 (2019)
Acknowledgements
The authors are grateful to the anonymous referees for their valuable comments, which largely improve the quality of this paper. This work was supported by Startup Foundation for Introducing Talent of NUIST grant 2020r003, National Natural Science Foundation of China grant 11771078, Natural Science Foundation of Jiangsu Province grant BK20181258, and National Research Foundation of Singapore grant NRF-RSS2016-004.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 A.1 Proof of Lemma 3
Proof
Since \(\nabla f\) is Lipschitz continuous with the modulus \(L_f\), it follows from Lemma 1 that
On the other hand, recall that \(f=f_1-f_2\) with \(f_1\) and \(f_2\) being convex, and their gradients \(\nabla f_1\) and \(\nabla f_2\) being Lipschitz continuous with moduli \(L_f\) and \(l_f\), respectively, thus we have
Summing the above two inequalities, and associating with \(f=f_1-f_2\) and \(\nabla f=\nabla f_1-\nabla f_2\), we get
Next, from the minimization subproblem (9c), and the fact that \(D_h(x^{k},x^k)=0\) by the definition in (8), we have
Rearranging the terms, we obtain
Combining the inequalities (30), (31) and (32) and recalling \(F:=f+g\), we obtain
Next, recall that \(\varDelta _k:=x^k-x^{k-1}\) in (13), then it follows from (9a) and (9b) that
and
Substituting the above equalities into (33), we have
where the second inequality follows from the \(\sigma _h\)-strong convexity of h, i.e.,
and the last inequality follows from \(\beta _k L_f \le \frac{\alpha _k}{\lambda _k}\) (see Assumption 2) and
Then, by the definition of \(\delta _k\) in (14) and the nondecreasing behavior of \(\{\lambda _k\}\) in Assumption 2, we get
From the definition of \(H_{\delta _k}(x^{k},x^{k-1})\) in (14) and the condition \(\beta _k \le {L_f}/{(L_f+l_f)}\) in Assumption 2, we obtain
Moreover, by the condition (10), it holds that
Then, we have
Together with (35), we get the assertion (12) immediately. Furthermore, it follows from \(-\frac{\varepsilon }{2\lambda _k}<0\) by Assumption 2 that \(\{H_{\delta _k}(x^{k},x^{k-1})\} \) is monotonically nonincreasing. This completes the proof. \(\square \)
1.2 A.2 Proof of Theorem 1
Proof
(i) For any initial point \(x^0\in {\mathbb {R}}^n\), we know that \(x^1\in \mathrm{dom}F\) and thus \(F(x^1)<\infty \). It follows from Lemma 3 that the sequence \(\{H_{\delta _k}(x^{k},x^{k-1})\} \) is monotonically nonincreasing, thus we have
Thus the sequence \(\{x^k\}_{k\ge 1}\) is contained in the level set \(\{x\in {\mathbb {R}}^n\,|\,F(x)\le F(x^1)\}\), which is bounded regardless of the choice of \(x^0\) by the coercivity of F in Assumption 1. This is enough for showing that the whole sequence \(\{x^k\}_{k\ge 0}\) is bounded.
(ii) We first conclude that there exists an upper bound \({\bar{\lambda }} = {\sigma _h}/{L_f}\) such that \(\lambda _k\le {\bar{\lambda }}\) for any \(k \ge 0\) from the condition (10). Otherwise, there is a \(k_0 \ge 0\) such that for any \(k \ge k_0\)
Obviously, there is no \(\beta _k\) satisfying the above inequalities. Therefore, we have \(\lambda _k\le {\bar{\lambda }}=\sigma _h/L_f\) and it holds that \(\frac{\varepsilon }{2\lambda _k}\ge \frac{\varepsilon }{2{\bar{\lambda }}}\). Summing up (12) with \(k=1,2,\ldots ,N\) and combining the inequality \(\frac{\varepsilon }{2\lambda _k}\ge \frac{\varepsilon }{2{\bar{\lambda }}}\) yield that
Letting N tend to \(\infty \) and recalling that \(\varepsilon >0\) and \({\bar{\lambda }} >0\), the assertion (ii) follows directly.
(iii) From the definition of \(H_{\delta _k}(x^k,x^{k-1})\) in (14), we know that \(\{H_{\delta _k}(x^k,x^{k-1})\}\) is bounded from below since \(F\ge {\underline{F}}>-\infty \). On the other hand, it follows from Lemma 3 that \(\{H_{\delta _k}(x^k,x^{k-1})\}\) is monotonically nonincreasing, hence \(\{H_{\delta _k}(x^k,x^{k-1})\}\) is convergent. This together with the boundedness of \(\delta _k\),
and \(\lim _{k\rightarrow \infty }\Vert \varDelta _k\Vert =0\) in the assertion (ii), we obtain that \(\{F(x^k)\}\) is convergent.
(iv) Since \(\{x^k\}\) is bounded, there exists at least one cluster point. Let \({\tilde{x}}\) be a cluster point and \(\{x^{k_n}\}\) be the subsequence of \(\{x^k\}\) such that \(\lim _{n\rightarrow \infty }x^{k_n}={\tilde{x}}\). From the iterative step (9c), we know that for any integer k,
Then, we have
Using the fact \(D_h(x^{k+1},x^k)\ge \frac{\sigma _h}{2}\Vert x^{k+1}-x^k\Vert ^2\) and choosing \(k:=k_n-1\,(n\ge 1)\), we obtain
By taking the superior limit above as \(n\rightarrow \infty \), and using the fact in (ii), the continuity of \(\nabla f\) and h, \(x^{k_n}\rightarrow {\tilde{x}}\) as \(n\rightarrow \infty \), and the fact that \(\{z^k\}\) is bounded and so is \(\nabla f(z^k)\), we have
On the other hand, by the lower semicontinuity of g, we get
Hence, we have \( \lim _{n\rightarrow \infty } g(x^{k_n}) = g({\tilde{x}}).\) Together with the definition of F in (1) and the continuity of f, we have
Define \(\xi ^{k_n}:= -\frac{1}{\lambda _{k_n-1}}\left[ (x^{k_n-1}-y^{k_n-1})-(\nabla h(x^{k_n})-\nabla h(x^{k_n-1}))\right] +\nabla f(x^{k_n})-\nabla f(z^{k_n-1}),\,n\ge 1\). Then, by the optimality condition (11), we have
Recalling (9a) and (9b), \(\lim _{n\rightarrow \infty }\Vert \varDelta _{k_n}\Vert =0\) by statement (ii), the continuity of \(\nabla h\) and \(\nabla f\), and the boundedness of \(\{\alpha _{k}\}\), \(\{\beta _{k_n}\}\) and \(\{\lambda _{k_n}\}\) by Assumption 2, we get \(\lim _{n\rightarrow \infty }\xi ^{k_n}=0\). Together with \(\lim _{n\rightarrow \infty }x^{k_n}= {\tilde{x}}\), (36) and (37), we obtain
which implies that \({\tilde{x}}\in \mathrm{crit}F\). Furthermore, it is easy to derive that F is finite and constant on the set of all cluster point \({\tilde{x}}\) from Assumption 1 and the above conclusions as that in [13, Lemma 5]. This completes the proof. \(\square \)
Rights and permissions
About this article
Cite this article
Wu, Z., Li, C., Li, M. et al. Inertial proximal gradient methods with Bregman regularization for a class of nonconvex optimization problems. J Glob Optim 79, 617–644 (2021). https://doi.org/10.1007/s10898-020-00943-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10898-020-00943-7