The Hosoya index and the Merrifield–Simmons index

Abstract

In this article, we give sharp bounds on the Hosoya index and the Merrifield–Simmons index for connected graphs of fixed size. As a consequence, we determine all connected graphs of any fixed order and size which maximize the Merrifield–Simmons index. Sharp lower bounds on the Hosoya index are known for graphs of order n and size $m\in [n-1,2n-3]\cup \left( {n-1\atopwithdelims ()2},{n\atopwithdelims ()2}\right]$; while sharp upper bounds were only known for graphs of order n and size $m\le n+2$. We give sharp upper bounds on the Hosoya index for dense graphs with $m\ge {n\atopwithdelims ()2}-2n/3$. Moreover, all extreme graphs are also determined.

1 Introduction

We consider simple graphs, namely graphs without loops or multiple edges in this article. Let $G=(V,E)$ be a graph. The order of G is |V| and the size of G is |E|. Denote by $G^c$ the complement of G. For a vertex $v\in V$, we denote by $N_G(v)$ (or simply N(v)) the neighborhood of v in G and the degree of v is |N(v)|. A matching of G is a set of disjoint edges in G and a stable set of G is a subset of vertices which induces an edgeless subgraph. The Hosoya index of G, denoted by Z(G), is the number of all matchings in G. The Merrifield–Simmons index or Fibonacci number of G, denoted by F(G), is the number of all stable sets in G; and let c(G) be its complement, i.e., the number of all cliques in G. For simplicity, we write c(U) instead of c(G[U]), where G[U] is a subgraph of G induced by a subset U of V. Denote by $K_n$, $P_n$, and $S_n$, a complete graph, a path, and a star of order n respectively. A graph of order n and size m is called almost complete if $m>{n-1\atopwithdelims ()2}$. Let $f_n=\frac{1}{\sqrt{5}}\left[ \left( \frac{1+\sqrt{5}}{2}\right) ^n-\left( \frac{1-\sqrt{5}}{2}\right) ^n\right]$ be the nth Fibonacci number throughout.

The Hosoya index was first introduced in 1971 by Hosoya [7] as a molecular-graph based structure descriptor, which he named topological index. Hosoya showed that certain physico-chemical properties of alkanes (in particular, their boiling points) are well correlated with this index. On the other hand, the Merrifield–Simons index introduced by Merrifield and Simmons in 1980s [10, 11] is also known as the Fibonacci number of a graph introduced by Prodinger and Tichy [16] in the literature of mathematics. Enlightening connections of these two indices are observed in the literature. The most direct connection is that for a graph G and its line graph L(G), we have $F(L(G))=Z(G)$ by their definitions. Moreover, it is discovered that heuristically speaking, the graph with maximum Hosoya index is similar to the graph with minimum Merrifield–Simmons index; and the graph with minimum Hosoya index is similar to the graph with maximum Merrifield–Simmons index. For example, Gutman [6] in 1977 proved that the path is the tree that maximizes the Hosoya index and the star is the tree that minimizes it; while Prodinger and Tichy [16] in 1982 proved that the path minimizes the Merrifield–Simmons index and the star maximizes it among all trees of fixed order. The same pattern also exists in unicyclic graphs and bicyclic graphs, see [1,2,3,4,5, 12, 13, 15, 19, 20, 22]. However, Liu et al. [8] in 2015 showed that different patterns appear in tricyclic graphs. Let us summarize the case of trees as a theorem which is used later on.

Theorem 1

[6, 16] Among all trees of order n, the star $S_n$ minimizes the Hosoya index and maximizes the Merrifield–Simmons index, while the path $P_n$ maximizes the Hosoya index and minimizes the Merrifield–Simmons index. Moreover, $F(S_n)=2^{n-1}+1$, $Z(S_n)=n$, $F(P_n)=f_{n+2}$, and $Z(P_n)=f_{n+1}$.

For simplicity, we call a graph maximizer if it maximizes the corresponding index. The minimizer is similarly defined. It is clear that $c(G)\ge n+m+1$ for a graph G of order n and size m. Considering the complement, we have $F(G)\ge {n\atopwithdelims ()2}+n-m+1$ for $m\ge \frac{n^2}{4}-\frac{n}{2}$ with equality if and only if the largest stable set of G has at most two vertices. On the other hand, Zhao and Liu [23] in 2006 determined the connected graph of order n and size m that maximizes the Merrifield–Simmons index for $m\le 2n-3$. In 2007, Wood [21] gave a sharp upper bound on the Merrifield–Simmons index for all possible values of m in its complement form. Extending their results, we establish sharp bounds on these indices for connected graphs of fixed size.

Theorem 2

Let G be a connected graph of size m and let $\gamma =(1+\sqrt{1+8m})/2$. The following statements hold.

• 1. ${\lceil \gamma \rceil +1\atopwithdelims ()2}-m+1\le F(G)\le 2^m+1$. The first equality holds if and only if G is almost complete and $G^c$ is triangle-free, and the second equality holds if and only if G is a star.

• 2. $m+1 \le Z(G)\le f_{m+2}=\frac{1}{\sqrt{5}}\left[ \left( \frac{1+\sqrt{5}}{2}\right) ^{m+2}-\left( \frac{1-\sqrt{5}}{2}\right) ^{m+2}\right]$. The first equality holds if and only if G is a star or a triangle, and the second equality holds if and only if G is a path.

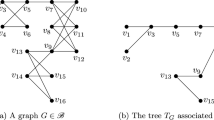
• 3. $\left\lceil (\sqrt{m} + 1)^2 \right\rceil \le c(G)\le 2^{\lfloor \gamma \rfloor }+2^{m-{\lfloor \gamma \rfloor \atopwithdelims ()2}}(\lceil \gamma \rceil -\lfloor \gamma \rfloor )$. The first equality holds if and only if G is a triangle-free graph of order $\lceil 2\sqrt{m}\rceil$, and the second equality holds if and only if G has such a vertex v that $G-v$ is complete or G consists of a clique and two more arbitrarily inserted edges (see Fig. 1 for example).

Fig. 1

A clique $K_4$ with two arbitrarily inserted edges

As a consequence of Theorem 2, we obtain the following complement form of the Wood upper bound [21] with all the determined maximizers.

Corollary 1

[21] If G is a connected graph of order n and size m and $\gamma =\frac{1}{2}\left( 1+\sqrt{1+8\left[ {n\atopwithdelims ()2}-m\right] }\right)$, then $F(G)\le 2^{\lfloor \gamma \rfloor }+2^{{n\atopwithdelims ()2}-m-{\lfloor \gamma \rfloor \atopwithdelims ()2}}(\lceil \gamma \rceil -\lfloor \gamma \rfloor )+ n - \lceil \gamma \rceil$ with equality if and only if $G^c$ consists of isolated vertices and one of the following graphs (see Fig. 2 for example with $n=6$):

• a maximizer in Theorem 2 (3),

• a disjoint union of a clique and one clique or two cliques of order two,

• a disjoint union of a clique and a path of length two,

• a disjoint union of a clique with a pendent edge and a clique of order two.

Fig. 2

Four types of $G^c$ described in Corollary 1 for $n=6$

In 2010, Pan and Sun [14] also determined the connected graph of order n and size m that minimizes the Hosoya index for $m\le 2n-3$. Again these extreme graphs are quite similar to those with the largest Merrifield–Simons index in [23]. In 2015, So and Wang [17] determined the minimizers for $m>{n-1\atopwithdelims ()2}$ in a stronger form. Extending their results, we give sharp upper bounds on the Hosoya index for dense graphs.

Theorem 3

Let G be a connected graph of order n and size m. The following statements hold.

• 1. If $m\ge {n\atopwithdelims ()2}-\frac{n}{2}$ and M is a matching of size ${n\atopwithdelims ()2}-m$ in the complete graph $K_n$, then $Z(G)\le Z(K_n-M)$ with equality if and only if G is isomorphic to $K_n-M$.

• 2. If ${n\atopwithdelims ()2}-\frac{2n}{3}\le m<{n\atopwithdelims ()2}-\frac{n}{2}$, then Z(G) is maximized by such a graph G that $G^c$ is a disjoint union of paths of length one or two.

More extreme results on these two indices for other class of graphs can be found in the survey [18]. In order to prove our theorems, we need a simple lemma which follows directly from the definitions.

Lemma 1

If uv is an edge of a graph G, then the following equalities hold:

• $c(G)=c(G-v)+c(N(v))=c(G-uv)+c(N(u)\cap N(v))$;

• $F(G)=F(G-v)+F(G-N(v))=F(G-uv)-F(G-N(u)-N(v))$;

• $Z(G) = Z(G-uv) + Z(G-u-v)$.

Corollary 2

If H be a subgraph of G, then $Z(H)\le Z(G)$ with equality if and only if $E(G)=E(H)$. Moreover, if H is a proper induced subgraph of G, then $c(H)<c(G)$ and $F(H)>F(G)$.

The proof of Theorem 2 is presented in Sect. 2 and the proofs of Corollary 1 and Theorem 3 are presented in Sect. 3 respectively.

2 Graphs of fixed size

Proof of Theorem 2

Let n be the order of G. We prove the three items successively.

Item 1. Since G is connected, we have $m\ge n-1$. For $m\ge n$, it is obvious that $F(G)\le 2^m$. For $m=n-1$, the graph G is a tree. The upper bound follows from Theorem 1 that $F(T)\le 2^m+1$ for all trees T with equality if and only if T is a star. For the lower bound, we have $F(G)\ge 1+n+|E(G^c)|=1+n+{n\atopwithdelims ()2}-m={n+1\atopwithdelims ()2}-m+1$. The desired inequality follows from $n\ge \lceil \gamma \rceil$ for $m\le {n\atopwithdelims ()2}$. For the equality, it is necessary and sufficient that $G^c$ is triangle-free and $n=\lceil \gamma \rceil$, i.e., G is almost complete.

Item 2. Note that Z(G) is the Merrifield–Simmons index of the line graph L(G). Since L(G) is of order m, from the proof of Item 1 we have $Z(G)=F(L(G))\ge 1+m+|E(L(G)^c)|\ge m+1$ with equality if and only if L(G) is complete, which for $m\ne 3$ is equivalent to G being a star. For $m=3$, the graph G can be either a star or a triangle. For the upper bound, let $G^*$ be the maximizer. We claim that every edge of $G^*$ is a bridge. Indeed suppose to the contrary that uv is an edge of $G^*$, but not a bridge in $G^*$. Deleting the edge uv and inserting a new vertex x and a new edge vx to $G^*$ result in a connected graph G of size m with

$$\begin{aligned}Z(G)=Z(G-vx)+Z(G-v-x)=Z(G^*-uv)+Z(G^*-v).\end{aligned}$$

Since $G^*-uv$ is connected, the vertex u must be incident with some other edge besides uv. It turns out that $G^*-u-v$ is a proper subgraph of $G^*-v$, which with Corollary 2 and Lemma 1 implies $Z(G)>Z(G^*-uv) + Z(G^*-u-v)=Z(G^*)$, contrary to the maximality of $G^*$. Thus $G^*$ is a tree and in fact it is a path with $Z(G^*)=Z(P_{m+1})=f_{m+2}$ by Theorem 1.

Item 3. First we establish the lower bound on c(G). This is done by showing that c(G) is minimized by a triangle-free graph. If G has a triangle, say uvw, then deleting the edge uv and inserting a new vertex x and a new edge vx to G result in a connected graph H of size m. By Lemma 1, we have

$$\begin{aligned} c(G)= & {} c(G-uv)+c(N_G(u)\cap N_G(v)) \\= & {} c(H-x)+c(N_G(u)\cap N_G(v)) \\= & {} c(H)-c(N_H(x))+c(N_G(u)\cap N_G(v)). \end{aligned}$$

Observe that $N_H(x)=\{ v\}$ and $w\in N_G(u)\cap N_G(v)$. Applying Corollary 2, we obtain $c(N_G(u)\cap N_G(v))\ge c(\{w\}) = 2 = c(N_H(x))$ and so $c(G)\ge c(H)$. Since there are (strictly) less triangles and more leaves (i.e., vertices of degree one) in H than in G, one can repeat this process to obtain a triangle-free graph $G'$ of size m so that $c(G')\le c(G)$. By the Mantel theorem [9], we have

$$\begin{aligned} c(G')\ge m+n+1\ge m+\lceil 2 \sqrt{m}\rceil +1=\left\lceil (\sqrt{m}+1)^2\right\rceil . \end{aligned}$$

(1)

It is readily verified that any triangle-free graph of order $\lceil 2\sqrt{m}\rceil$ and size m attains the lower bound. Conversely, we claim that each minimizer must be triangle-free of order $\lceil 2\sqrt{m}\rceil$. By Eq. (1), it is clear that any graph attaining the lower bound is of order $\lceil 2\sqrt{m}\rceil$. Let $G^*$ be a minimizer of size m and so $|V(G^*)|=\lceil 2\sqrt{m}\rceil$. It suffices to show that $G^*$ is triangle-free. This is trivial for $m\le 4$. For $m\ge 5$, suppose to the contrary that uvw is a triangle in $G^*$. Since $w\in N_{G^*}(u)\cap N_{G^*}(v)$, we have $c(N_{G^*}(u)\cap N_{G^*}(v))\ge 2$ and

$$\begin{aligned} \left\lceil (\sqrt{m}+1)^2\right\rceil =c(G^*)=c(G^*-uv)+c(N_{G^*}(u)\cap N_{G^*}(v))\ge \left\lceil (\sqrt{m{-}1}{+}1)^2\right\rceil +2 \end{aligned}$$

(2)

which implies $\lceil 2\sqrt{m}\rceil \ge \lceil 2\sqrt{m-1}\rceil +1$. Meanwhile, we have the elementary estimation

$$\begin{aligned} 2\sqrt{m}-2\sqrt{m-1}=\frac{2}{\sqrt{m}+\sqrt{m-1}}\le \frac{2}{\sqrt{5}+2}<1 \end{aligned}$$

and hence,

$$\begin{aligned} \left\lceil 2\sqrt{m}\right\rceil -\left\lceil 2\sqrt{m-1}\right\rceil \le \left\lceil 2\sqrt{m-1}+1\right\rceil -\left\lceil 2\sqrt{m-1}\right\rceil = 1. \end{aligned}$$

Thus the equality holds in Eq. (2), which implies that $G^*-uv$ is also a minimizer of size $m-1$ and order $\lceil 2\sqrt{m-1}\rceil$. But this contradicts the fact that $G^*-uv$ is a spanning subgraph of $G^*$ of order $\lceil 2\sqrt{m}\rceil$.

Secondly we show the upper bound. For simplicity, we define a map $f:{\mathbb {Z}}_+ \rightarrow {\mathbb {Z}}_+$ by

$$\begin{aligned} f(n)=\left\{ \begin{array}{ll} 0,&{}\quad n=0,\\ 2^n,&{}\quad n>0. \end{array}\right. \end{aligned}$$

Note that f is convex, i.e., $f(u)-f(u-s)\ge f(v)-f(v-s)$ for $u\ge v\ge s$. Denote by $\gamma _n, r_n$ the unique pair of integers satisfying $0\le r_n <\gamma _n$ and $n={\gamma _n\atopwithdelims ()2}+r_n$. With the above notations, let $c^*(m) = 2^{\gamma _m}+f(r_m)$. For $m\le 5$, the upper bound is trivial. Now we assume that $m\ge 6$ and $\gamma _m\ge 4$ and use induction on m. If G has a cut vertex, say v, then G can be covered by two connected subgraphs, say $G_1$ and $G_2$ with $V(G_1)\cap V(G_2)=\{ v\}$ and $E(G)=E(G_1)\cup E(G_2)$. Observe that $c(G)=c(G_1)+c(G_2)-2$. Denote by p and q the sizes of $G_1$ and $G_2$ respectively. By the induction hypothesis, we have

$$\begin{aligned} c(G)\le c^*(p) + c^*(q) - 2 = 2^{\gamma _p} + 2^{\gamma _q} + f(r_p) + f(r_q) -2. \end{aligned}$$

Let $S(m,p,q)=c^*(m)-c^*(p)-c^*(q)+2=2^{\gamma _m}+f(r_m)-[2^{\gamma _p}+2^{\gamma _q}+f(r_p)+f(r_q)-2]$. It suffices to prove

$$\begin{aligned} S\ge 0 \text{ for } \text{ all } m=p+q. \end{aligned}$$

(3)

We may assume that $r_p=r_q=0$. In fact, note that $\gamma _m\ge \max \{\gamma _p,\gamma _q\}$. If $r_m\ge r_p$, then by the convexity of f, we have

$$\begin{aligned} f(r_m)-f(r_p)\ge f(r_m-r_p)-f(0) = f(r_m-r_p). \end{aligned}$$

Hence, $S(m,p,q) \ge S(m-r_p, p-r_p, q)$. The new remainder term $r_{p-r_p}$ turns out to be 0 and the new $\gamma _{p-r_p}=\gamma _p$. If $r_m<r_p$, then we obtain from the convexity of f and the fact $r_p<\gamma _p$ that

$$\begin{aligned} f(r_m) - f(r_p)\ge f(r_m + \gamma _p- r_p) - f(\gamma _p)=f(r_m+\gamma _p-r_p)-2^{\gamma _p}. \end{aligned}$$

Hence, $S(m,p,q)\ge S(m+\gamma _p-r_p, p+\gamma _p-r_p, q)$. The new remainder term $r_{p+\gamma _p - r_p}$ turns out to be 0 again and the new $\gamma _{p+\gamma _p - r_p}=\gamma _p+1>\gamma _p$. Applying the same procedure to q, we reduce to the case where $r_{p}=r_{q}=0$. Note that in this procedure, $\gamma _p$ and $\gamma _q$ are both nondecreasing. Without loss of generality, we may assume $p\le q$. If $\gamma _m \ge \gamma _q + 1$, then we have $2^{\gamma _p} + 2^{\gamma _q}\le 2^{\gamma _q+1}\le 2^{\gamma _m}$, thereby $S(m,p,q)\ge 2+f(r_m)>0$. The remaining case $\gamma _m = \gamma _q$ is possible only if $r_m = p <\gamma _q$. It follows that $S(m,p,q)=2^p-2^{\gamma _p} + 2$. By definition, it is evident that $\gamma _p\ge 2$. Thus $2^p - 2^{\gamma _p} + 2\ge 0$ follows from direct computation for $\gamma _p=2$ and from $p=\gamma _p(\gamma _p-1)/2\ge \gamma _p(3-1)/2=\gamma _p$ otherwise.

So we can assume that G has no cut vertex. Since $m\le {n\atopwithdelims ()2}$, we have $\gamma _m\le n$. If $\gamma _m=n$ then G is complete and the upper bound holds trivially. Thus we may assume $\gamma _m\le n-1$. Now choose a vertex v with minimum degree $\delta$ in G. Since $\delta \le 2m/n<\gamma _m(\gamma _m + 1)/n\le \gamma _m$, we see $\delta \le \gamma _m -1$ and so $\gamma _{m-\delta }\ge \gamma _m - 1$. By Lemma 1 and the induction hypothesis, we obtain

$$\begin{aligned} c(G) = c(G-v) + c(N(v))\le c^*(m-\delta ) + 2^\delta . \end{aligned}$$

(4)

Now it suffices to prove $2^{\gamma _{m-\delta }} + f(r_{m-\delta }) + 2^\delta \le 2^{\gamma _m} + f(r_m)$. For $\delta \le r_m$, it simplifies to

$$\begin{aligned} f(r_m - \delta )+f(\delta )\le f(r_m) \end{aligned}$$

(5)

which follows directly from the convexity of f. For $r_m<\delta \le \gamma _m-1$, we need to show

$$\begin{aligned} f(\gamma _m -1)-f(\gamma _m -1-(\delta -r_m))\ge f(\delta )-f(r_m) \end{aligned}$$

(6)

which follows from $\gamma _m -1\ge \delta$ and once again the convexity of f.

Finally we determine the maximizer G. If G has a cut vertex, then all equalities in the proof of $S(m,p,q)\ge 0$ must be attained. Recall that in the reduction to $\gamma _p=2$, the procedure keeps $\gamma _p$ nondecreasing. Thus $\gamma _p\le 2$ for the original graph G. But by definition $\gamma _p\ge 2$, so $\gamma _p=2$ remains true for G. Consequently we have $p=1$ or 2. As we assumed $\gamma _m\ge 4$, we see that $\gamma _q\ge 3$, and $\gamma _m\le \gamma _q +1$. If $\gamma _m=\gamma _q+1$, then we consider the following two cases.

Case 1. $p=1$.

In this case, we have

$$\begin{aligned} p+q=1+{\gamma _q\atopwithdelims ()2}+r_q=m={\gamma _q+1\atopwithdelims ()2}+r_m, \end{aligned}$$

which implies that $r_q=\gamma _q+r_m-1$. Since $r_q\le \gamma _q-1$, we obtain that $r_m=0$ and $r_q=\gamma _q-1$.

Case 2. $p=2$.

Similarly, the equality $p+q=m$ leads to $r_q=\gamma _q+r_m-2$, whence $r_m=0$, $r_q=\gamma _q-2$ or $r_m=1$, $r_q=\gamma _q-1$.

For both cases, it is easy to verify the strict inequality. Consequently $\gamma _m<\gamma _q+1$. But $m>q$ implies $\gamma _m\ge \gamma _q$, so $\gamma _q=\gamma _m\ge 4$. For $r_q=0$, the equality in Eq. (3) holds for both $p=1$ and $p=2$. For $r_q\ge 1$, the equality in Eq. (3) becomes $2^{r_q}=2$ if $p=1$ and $3\cdot 2^{r_q}=4$ if $p=2$. The latter one is obviously impossible and the former one is possible only if $p=r_q=1$. To conclude, either $r_q=0$ and by the induction hypothesis $G_2$ is a clique, or $p=r_q=1$ and $G_2$ is a clique with a pendent edge (see Fig. 3). In both cases, the graph G is a clique with one or two arbitrarily inserted edges.

Fig. 3

A clique $K_4$ with a pendent edge

If G has no cut vertex, then by checking the condition of equalities in Eqs. (4), (5), and (6), we see that all possible cases are $\delta =r_m$, or $r_m=2$ and $\delta =1$, or $\delta =\gamma _m-1$. For the first case, by the induction hypothesis, $G-v$ is complete. For the second case, $G-v$ is a clique with a pendent edge, so G is a clique with two arbitrarily inserted edges. For the third case, G is complete. $\square$

3 Graphs of fixed order and size

Proof of Corollary 1

First note that $m\ge n-1$ for G is connected. Let $G_0$ be the maximizer and assume that $F_1,F_2,\ldots ,F_k$ are all the components of order greater than one in $G_0^c$. If $k=1$, then by applying Theorem 2 (3), we may construct a graph H of order n such that $H^c$ consists of isolated vertices and a component $F_1^*$ of size $m'={n\atopwithdelims ()2}-m$ with $c(F_1^*)=c^*(m')$, where the function $c^*$ is defined in the proof of Theorem 2. Obviously, $c(F_1)\le c(F_1^*)$ and $|V(F_1^*)|\le |V(F_1)|$. Thus the number of isolated vertices in $H^c$ is no less than that in $G_0^c$. Combining these two facts we have $F(H)=c(H^c)\ge c(G_0^c)=F(G_0)$ with equality if and only if $F_1$ is a maximizer in Theorem 2 (3) as desired.

So we may assume that $k\ge 2$. The disjoint union of two graphs $G_1$ and $G_2$ is $G_1\cup G_2=(V(G_1)\cup V(G_2),E(G_1)\cup E(G_2))$. The adjoin $G_1\cdot G_2$ is obtained from $G_1$ and $G_2$ by identifying a vertex of $G_1$ with a vertex of $G_2$. The adjoin of two graphs is not necessarily unique. Let v be the identified vertex in $G_1\cdot G_2$. By Lemma 1, we have

$$\begin{aligned} c(G_1\cdot G_2)= & {} c(G_1\cdot G_2-v)+c(N(v)) \\= & {} c(G_1-v)+c(G_2-v) - 1 + c(N_{G_1}(v))+c(N_{G_2}(v)) - 1 \\= & {} c(G_1-v)+c(N_{G_1}(v)) + c(G_2-v) + c(N_{G_2}(v)) - 2 \\= & {} c(G_1) + c(G_2) - 2 = c(G_1\cup G_2) - 1. \end{aligned}$$

Inductively we may define the adjoin $G_1\cdot G_2\cdots G_l$ of k graphs $G_1, G_2,\ldots ,G_l$ as the adjoin of the two graphs $G_l$ and $G_1\cdot G_2\cdots G_{l-1}$. By induction, it is easy to see that

$$\begin{aligned} c(G_1\cdot G_2\cdots G_l)=c\left( \bigcup _{i=1}^l G_i\right) -(l-1). \end{aligned}$$

Now let H be a graph of order n consisting of the adjoin of $F_1, \ldots , F_k$ and isolated vertices. It is easy to check that H has $k-1$ more isolated vertices than $G^c$, thus we have

$$\begin{aligned} c(H)-c(G^c)=c(F_1\cdot F_2\cdots F_k)+(k-1)-c\left( \bigcup _{i=1}^k F_i\right) =0 \end{aligned}$$

Replacing G by $H^c$, we reduce to the case $k=1$. The upper bound is now proved. If the equality holds for $k\ge 2$, then H consists of isolated vertices and a large component $F=F_1\cdot F_2\cdots F_k$, which is a maximizer in Theorem 2 (3). This is possible only if $|E(F)|={l\atopwithdelims ()2}+1$ or ${l\atopwithdelims ()2}+2$ for some $l\in {\mathbb {N}}$ by the structure of the maximizer F. In the former case, F can only be the adjoin of $K_2$ and a clique, both of which cannot be the adjoin of two connected graphs of order at least two. So $k=2$ and $G^c$ consists of an isolated edge, a clique, and isolated vertices. In the latter case, F can only be the adjoin of a clique and a path of length two, or $K_2$ and a clique with a pendent edge. Thus $G^c$ must be the extreme graphs described in the theorem. $\square$

Lemma 2

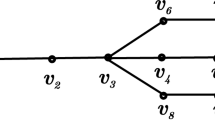
Let G be such a graph that $G^c$ has an isolated vertex v and a vertex u with $N_{G^c}(u)=\{w_1,\ldots ,w_k\}$ and $k\ge 2$. If H is a graph obtained from G by replacing the edge $vw_1$ by a new edge $uw_1$, see Fig. 4, then $Z(G)<Z(H)$.

Fig. 4

The local structures of $G^c$ and $H^c$ in Lemma 2

Proof

By Lemma 1, we have $Z(G)=Z(G-vw_1)+Z(G-v-w_1)$ and $Z(H)=Z(H-uw_1)+Z(H-u-w_1)$. Note that $G-vw_1=H-uw_1$. Moreover, we have $Z(G-v-w_1)<Z(H-u-w_1)$ since $G-v-w_1$ is a proper subgraph of $H-u-w_1$ for $k\ge 2$. Thus $Z(G)<Z(H)$. $\square$

Lemma 3

Let G be a graph of order n and size m. If G has no component of order at most two, then $m\ge 2n/3$ with equality if and only if G is a disjoint union of paths of length two.

Proof

Let k be the number of components of G. If G has no component of order at most two, then $k\le n/3$ and $m\ge n-k\ge 2n/3$ with equality if and only if every component of G is a path of order three. $\square$

Lemma 4

Let G be such a graph that $G^c$ has a vertex u with $N_{G^c}(u)=\{v_1,\ldots ,v_k\}$, $k\ge 2$ and a component of order 2, say $w_1w_2$. If H is a graph obtained from G by replacing the edge $v_1w_1$ by a new edge $uv_1$, see Fig. 5, then $Z(G)\le Z(H)$ with equality if and only if $k=2$ and $N_{G^c}(v_2)\subset \{u,v_1\}$.

Fig. 5

The local structures of $G^c$ and $H^c$ in Lemma 4

Proof

Note that $G-v_1w_1=H-uv_1$. By Lemma 1, we get

$$\begin{aligned} Z(G)-Z(H)= & {} Z(G-v_1w_1)+Z(G-v_1-w_1)-[Z(H-uv_1)+Z(H-u-v_1)] \\= & {} Z(G-v_1-w_1)-Z(H-u-v_1)\\= & {} Z(G-v_1-w_1+uv_2)-Z(G-v_1-w_1-u-v_2)\\&-[Z(H-u-v_1+w_1w_2)-Z(H-u-v_1-w_1-w_2)]. \end{aligned}$$

Note that $G-v_1-w_1+uv_2$ is isomorphic to $H-u-v_1+w_1w_2-\sum \nolimits _{i=3}^kv_i w_1$ which is a subgraph of $H-u-v_1+w_1w_2$. If $k=2$, then the two graphs are identical. Thus $Z(G-v_1-w_1+uv_2)\le Z(H-u-v_1+w_1w_2)$ with equality if and only if $k=2$. On the other hand, $H-u-v_1-w_1-w_2$ is a subgraph of $G-v_1-w_1-u-v_2$. The two graphs are isomorphic if and only if the vertex $v_2$ is isolated in $G^c-u-v_1$. Hence, $Z(G-v_1-w_1-u-v_2)\ge Z(H-u-v_1-w_1-w_2)$ with equality if and only if $N_{G_1^c}(v_2)\subset \{u,v_1\}$. Thus $Z(G)\le Z(H)$ with equality if and only if $k=2$ and $N_{G^c}(v_2)\subset \{u,v_1\}$. $\square$

Lemma 5

Let H be an arbitrary graph and let G(k, l) be such a graph that $G^c(k,l)=H\cup P_k\cup P_l$. If $k\ge l+2$, then $Z(G(k,l))<Z(G(k-1,l+1))$.

Proof

Denote by $u_1$ an end vertex of $P_k$ with its neighbor $u_2$ in $G^c(k, l)$. Also denote by $v_1$ an end vertex of $P_{l+1}$ with its neighbor $v_2$ in $G^c(k-1, l+1)$. Note that $G(k-1,l+1)+v_1v_2$ and $G(k,l)+u_1u_2$ are isomorphic to each other. Hence,

$$\begin{aligned} Z(G(k, l))-Z(G(k-1, l+1))= & {} Z(G(k,l)+u_1u_2)-Z(G(k,l)-u_1-u_2)\\&-[Z(G(k-1,l+1)+v_1v_2) \\&- Z(G(k-1,l+1) -v_1-v_2)]\\= & {} Z(G(k-1,l-1)) - Z(G(k-2,l)). \end{aligned}$$

Consequently, by Corollary 2 we have

$$\begin{aligned} Z(G(k,l)) - Z(G(k-1,l+1)) = Z(G(k-l,0)) - Z(G(k-l-1,1) < 0, \end{aligned}$$

since $G(k-l,0)$ is a proper subgraph of $G(k-l-1,1)$. $\square$

Proof of Theorem 3

We prove the two items successively.

Item 1. Let $G_0$ be the maximizer. If $m>{n\atopwithdelims ()2}-\frac{n}{2}$, then there exists an isolated vertex in $G_0^c$ and by Lemma 2, every vertex in $G_0^c$ is of degree no larger than 1. For $m={n\atopwithdelims ()2}-\frac{n}{2}$, if there is an isolated vertex in $G_0^c$, then $G_0^c$ has another vertex of degree more than 1 by the pigeonhole principle, which contradicts Lemma 2. Hence every vertex of $G_0^c$ has degree 1. In both cases, we deduce that $G_0$ is isomorphic to $K_n-M$.

Item 2. Let $G_1$ be the maximizer and $m'={n\atopwithdelims ()2}-m$. For $m<{n\atopwithdelims ()2}-\frac{n}{2}$, we have $m'>n/2$ and the complement $G_1^c$ has a vertex of degree larger than 1. Thus by Lemma 2, $G_1^c$ has no isolated vertex. First, when $m'<2n/3$, there exists a component of order 2 in $G_1^c$ by Lemma 3. In this case, every vertex with degree larger than 1 in $G_1^c$ is in a component of $K_3$ or $P_3$ in $G_1^c$ by Lemma 4. As a consequence, $G_1^c$ is just a disjoint union of triangles and paths of order 2 or 3. Denote by a, b, and c, the number of components of $K_2$, $P_3$, and $K_3$ in $G_1^c$ respectively. We have $2a+3b+3c=n$ and $a+2b+3c=m'$. It leads to $3c-a=3m'-2n<0$ and so $a>3c$. Suppose $c>0$. We have $a>0$. Let xyz be a triangle and uv be an isolated edge in $G_1^c$ and let $G_2=G_1+xy-vx$. It is easily verified that $Z(G_1)=Z(G_2)$ by Lemma 1. Along this procedure, pairs of $K_3$ and $K_2$ are converted to $P_5$ and one can finally obtain a connected triangle-free graph $G_3$ of order n and size m with $Z(G_3)=Z(G_1)$ and $G_3^c$ is a disjoint union of paths of order 2, 3, or 5. However, by Lemma 5, $Z(G_3)$ can be enlarged by averaging the length of the paths which contradicts our hypothesis that $G_1$ is the maximizer. Hence, $G_1^c$ is just a disjoint union of paths of order 2 or 3. Secondly consider $m'=2n/3$. If $G_1^c$ has a component of order 2, then analogous to the proof of the previous case one can deduce that $G_1^c$ is just a disjoint union of paths of order 2 or 3, which contradicts $m'=2n/3$. Thus $G_1^c$ has no component of order at most 2. By Lemma 3, in this case $G_1^c$ only consists of paths of length two. $\square$