Abstract
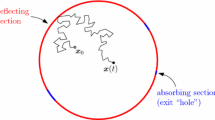
We consider Brownian motion in a circular disk Ω, whose boundary \(\partial\Omega\) is reflecting, except for a small arc, \(\partial\Omega_a\), which is absorbing. As \(\varepsilon=|\partial\Omega_a|/|\partial \Omega|\) decreases to zero the mean time to absorption in \(\partial\Omega_a\), denoted \(E\tau\), becomes infinite. The narrow escape problem is to find an asymptotic expansion of \(E\tau\) for \(\varepsilon\ll1\). We find the first two terms in the expansion and an estimate of the error. The results are extended in a straightforward manner to planar domains and two-dimensional Riemannian manifolds that can be mapped conformally onto the disk. Our results improve the previously derived expansion for a general domain, \(E\tau = {\frac{|\Omega|}{D\pi}}\big[\log{\frac{1}{\varepsilon}}+O(1)\big],\) (\(D\) is the diffusion coefficient) in the case of a circular disk. We find that the mean first passage time from the center of the disk is \(E[\tau\,|\,{\boldmath x}(0)={\bf 0}]={\frac{R^2}{D}}\big[\log{\frac{1}{\varepsilon}}+ \log 2 +{ \frac{1}{4}} + O(\varepsilon)\big]\). The second term in the expansion is needed in real life applications, such as trafficking of receptors on neuronal spines, because \(\log{\frac{1}{\varepsilon}}\) is not necessarily large, even when ε is small. We also find the singular behavior of the probability flux profile into \(\partial\Omega_a\) at the endpoints of \(\partial\Omega_a\), and find the value of the flux near the center of the window.
Similar content being viewed by others
References
A. Singer, Z. Schuss, D. Holcman and R. S. Eisenberg, Narrow Escape, Part I, (this journal).
J. D. Jackson, Classical Electrodymnics, 2nd Ed., Wiley, NY, 1975.
I. N. Sneddon, Mixed Boundary Value Problems in Potential Theory, Wiley, NY, 1966.
V. I. Fabrikant, Applications of Potential Theory in Mechanics, Kluwer, 1989.
V. I. Fabrikant, Mixed Boundary Value Problems of Potential Theory and Their Applications in Engineering, Kluwer, 1991.
A. I. Lur'e, Three-Dimensional Problems of the Theory of Elasticity, Interscience publishers, NY, 1964.
S. S. Vinogradov, P. D. Smith and E. D. Vinogradova, Canonical Problems in Scattering and Potential Theory, Parts I and II, Chapman & Hall/CRC, 2002.
H. L. F. von Helmholtz, Crelle, Bd. 7 (1860).
J. W. S. Baron Rayleigh, The Theory of Sound, Vol. 2, 2nd Ed., Dover, New York, 1945.
D Holcman and Z. Schuss, Escape Through a Small Opening: Receptor trafficking in a synaptic membrane. J. Stat. Phys. 117(5–6):975–1014 (2004).
A. J. Borgdorff and D. Choquet, Regulation of AMPA receptor lateral movements. Nature 417(6889):649–653 (2002).
A. I. Markushevich, Theory of Functions of a Complex Variable (3 Vols. in 1), American Mathematical Society, 2nd edition (1985).
A. Singer, Z. Schuss and D. Holcman, Narrow Escape, Part III: Non-smooth domains and Riemann surfaces, (this journal).
R. G. Pinsky, Asymptotics of the principal eigenvalue and expected hitting time for positive recurrent elliptic operators in a domain with a small puncture. Journal of Functional Analysis 2001:177–197, (2003).
I. V. Grigoriev, Y. A. Makhnovskii, A. M. Berezhkovskii and V. Y. Zitserman, Kinetics of escape through a small hole. J. Chem. Phys. 116(22):9574–9577 (2002).
L. Dagdug, A. M. Berezhkovskii, S. Y. Shvartsman and G. H. Weiss, Equilibration in two chambers connected by a capillary. J. Chem. Phys. 119(23):12473–12478 (2003).
Z. Schuss, Theory and Applications of Stochastic Differential Equations, Wiley Series in Probability and Statistics, Wiley, NY 1980.
C. Bender and S. Orszag, Advanced Mathematical Methods for Scientists and Engineers, McGraw-Hill, New York, 1987.
M. Abramowitz and I. A. Stegun, Handbook of Mathematical Functions, Dover Publications, NY, 1972.
V. A. Kozlov, V. G. Mazya and J. Rossmann, Elliptic Boundary Value Problems in Domains with Point Singularities, American Mathematical Society, Mathematical Surveys and Monographs, vol. 52, 1997.
V. A. Kozlov, J. Rossmann and V. G. Mazya, Spectral Problems Associated With Corner Singularities of Solutions of Elliptic Equations, Mathematical Surveys and Monographs, vol. 85, American Mathematical Society 2001.
M. Dauge, Elliptic Boundary Value Problems on Corner Domains: Smoothness and Asymptotics of Solutions, Lecture Notes in Mathematics, 1341, Springer-Verlag (1988).
A. P. Prudnikov, Y. A. Brychkov and O. I. Marichev, Integrals and Series, Vol. 1: Elementrary Functions, Gordon and Breach Science Publishers, 1986.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Singer, A., Schuss, Z. & Holcman, D. Narrow Escape, Part II: The Circular Disk. J Stat Phys 122, 465–489 (2006). https://doi.org/10.1007/s10955-005-8027-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10955-005-8027-5