Skip to main content
SpringerLink
Log in

Replicated INAR(1) Processes

  • Published:
Methodology and Computing in Applied Probability Aims and scope Submit manuscript

Abstract

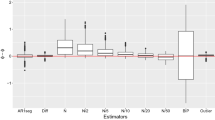
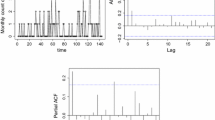
Replicated time series are a particular type of repeated measures, which consist of time-sequences of measurements taken from several subjects (experimental units). We consider independent replications of count time series that are modelled by first-order integer-valued autoregressive processes, INAR(1). In this work, we propose several estimation methods using the classical and the Bayesian approaches and both in time and frequency domains. Furthermore, we study the asymptotic properties of the estimators. The methods are illustrated and their performance is compared in a simulation study. Finally, the methods are applied to a set of observations concerning sunspot data.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • M. A. Al-Osh and A. A. Alzaid, “First-order integer-valued autoregressive (INAR(1)) process,” Journal of Time Series Analysis vol. 8 pp. 261–275, 1987.

    MathSciNet  MATH  Google Scholar 

  • A. Azzalini, “Replicated observations of low order autoregressive time series,” Journal of Time Series Analysis vol. 2 pp. 63–70, 1981.

    MathSciNet  Google Scholar 

  • A. Azzalini, “Estimation and hypothesis testing for collections of autoregressive time series,” Biometrika vol. 71 pp. 85–90, 1984.

    MathSciNet  Google Scholar 

  • K. Brännäs, “Explanatory variables in the AR(1) count data model,” Umeå Economic Studies vol. 381, pp. 1–16, 1995, Umeå, University.

    Google Scholar 

  • D. R. Brillinger, Time Series: Data Analysis and Theory, SIAM: Philadelphia, 2001.

    MATH  Google Scholar 

  • R. E. Chandler, “A spectral method for estimating parameters in rainfall models,” Bernoulli vol. 3 pp. 301–322, 1997.

    MATH  MathSciNet  Google Scholar 

  • P. Congdon, Applied Bayesian Modelling, John Wiley and Sons: Hoboken, NJ, 2003.

    MATH  Google Scholar 

  • S. Dégerine, “Maximum likelihood estimation of autocovariance matrices from replicated short time series,” Journal of Time Series Analysis vol. 8 pp. 135–146, 1987.

    MATH  MathSciNet  Google Scholar 

  • P. J. Diggle and I. al-Wasel, “Spectral analysis of replicated biomedical time series,” Applied Statistics vol. 46 pp. 31–71, 1997.

    MathSciNet  MATH  Google Scholar 

  • J.-P. Dion, G. Gauthier, and A. Latour, “Branching processes with immigration and integer-valued time series,” Serdica Mathematical Journal vol. 21 pp. 123–136, 1995.

    MathSciNet  MATH  Google Scholar 

  • J.-G. Du and Y. Li, “The integer-valued autoregressive (INAR(p)) model,” Journal of Time Series Analysis vol. 12 pp. 129–142, 1991.

    MathSciNet  MATH  Google Scholar 

  • K. O. Dzhaparidze and A. M. Yaglom, “Spectrum parameter estimation in time series analysis.” In P. R. Krishnaiah (ed.), Developments in Statistics, Vol. 4, pp. 1–96, Academic Press: New York, 1983.

    Google Scholar 

  • R. Fox and M. S. Taqqu, “Large sample properties of parameter estimates for strongly dependent stationary Gaussian time series,” The Annals of Statistics vol. 14, pp. 517–532, 1986.

    MathSciNet  MATH  Google Scholar 

  • J. Franke and T. Seligmann, “Conditional maximum likelihood estimates for INAR(1) processes and their application to modelling epileptic seizure counts.” In T. Subba Rao (ed.), Developments in Time Series Analysis, Chapmann and Hall, London. pp. 310–330, 1993

    Google Scholar 

  • J. Franke and T. Subba Rao, Multivariate first order integer valued autoregressions. Technical Report, Math Dep., UMIST, 1995

  • R. K. Freeland and B. P. M. McCabe, “Analysis of low count time series data by Poisson Autoregression,” Journal of the Time Series Analysis vol. 25 pp. 701–722, 2004

    MathSciNet  MATH  Google Scholar 

  • G. Gauthier and A. Latour, “Convergence forte des estimateurs des paramètrés d'un processus GENAR(p).” Annales des Sciences Mathématiques du Québec vol. 18 pp. 49–71, 1994.

    MathSciNet  MATH  Google Scholar 

  • A. E. Gelfand and A. F. M. Smith, “Sampling-based approaches to calculating marginal densities.” Journal of the American Statistical Association vol. 85, pp. 398–409, 1990.

    MathSciNet  MATH  Google Scholar 

  • W. R. Gilks and N. G. Best, “Adaptive rejection Metropolis sampling within Gibbs sampling.” Applied Statistics vol. 44 pp. 455–472, 1987.

    Google Scholar 

  • V. P. Godambe, “An optimum property of regular maximum likelihood estimation.” The Annals of Mathematical Statistics vol. 31, pp. 1208–1212, 1960.

    MathSciNet  Google Scholar 

  • E. J. Hannan, “The asymptotic theory of linear time series models,” Journal of Applied Probability vol. 10, pp. 130–145, 1973.

    MATH  MathSciNet  Google Scholar 

  • D. V. Hoyt and K. H. Schatten, “Group sunspot numbers: a new solar activity reconstruction,” Solar Physics vol. 181, pp. 491–512, 1998.

    Article  Google Scholar 

  • N. L. Johnson and S. Kotz, Distributions in Statistics: Discrete Distributions. John Wiley & Sons: New York, 1969.

    MATH  Google Scholar 

  • L. Klimko and P. Nelson, On conditional least square estimation for stochastic processes. The Annals of Statistics vol. 6, pp. 629–642, 1978.

    MathSciNet  MATH  Google Scholar 

  • A. Latour, “The Multivariate GINAR(p) process,” Advances in Applied Probability vol. 29 pp. 228–248, 1997.

    MATH  MathSciNet  Google Scholar 

  • A. Latour, “Existence and stochastic structure of a non-negative integer-valued autoregressive process,” Journal of Time Series Analysis vol. 19 pp. 439–455, 1998.

    Article  MATH  MathSciNet  Google Scholar 

  • Y. Park and C. W. Oh, “Some asymptotic properties in INAR(1) processes with Poisson marginals,” Statistical Papers vol. 38, pp. 287–302, 1997.

    Article  MathSciNet  MATH  Google Scholar 

  • J. Rice, “On the estimation of the parameters of a power spectrum,” Journal of Multivariate Analysis vol. 9 pp. 378–392, 1979.

    Article  MATH  MathSciNet  Google Scholar 

  • M. Rosenblatt, Markov Process—Structure and Asymptotic Behavior. Springer-Verlag: New York, 1971.

    Google Scholar 

  • M. Rosenblatt, “Cumulants and cumulant spectra.” In D. R. Brillinger and P. R. Krishnaiah (ed.), Handbook of Statistics, Vol. 3 Elsevier Science Publisher B. V., North Holland. pp. 369–382, 1983.

    Google Scholar 

  • S. A. O. Sesay and T. Subba Rao, “Frequency-domain estimation of bilinear time series models,” Journal of Time Series Analysis vol. 13 pp. 521–545, 1992.

    MathSciNet  MATH  Google Scholar 

  • I. Silva, Contributions to the analysis of discrete-valued time series. PhD Thesis submitted to Universidade do Porto, Portugal, 2005.

  • N. Silva, Análise Bayesiana de séries temporais de valores inteiros com observações repetidas. PhD Thesis submitted to Universidade de Aveiro, Portugal, 2005.

  • M. E. Silva and V. L. Oliveira, “Difference equations for the higher order moments and cumulants of the INAR(1) model,” Journal of the Time Series Analysis vol. 25, pp. 317–333, 2004.

    MATH  Google Scholar 

  • M. E. Silva and V. L. Oliveira, “Difference equations for the higher order moments and cumulants of the INAR(p) model.” Journal of the Time Series Analysis vol. 26 pp. 17–36, 2005.

    MathSciNet  MATH  Google Scholar 

  • F. W. Steutel, and K. Van Harn, “Discrete analogues of self-decomposability and stability.” The Annals of Probability vol. 7 pp. 893–899, 1979.

    MathSciNet  MATH  Google Scholar 

  • T. Subba Rao and R. E. Chandler, “A frequency domain approach for estimating parameters in point process models.” In P. Robinson and M. Rosenblatt (eds.), Athens Conference on Applied Probability and Time Series, Vol. II. Springer-Verlag, Lecture Notes in Statistics No. 115, pp. 392–405, 1996

  • A. M. Walker, “Asymptotic properties of least-squares estimates of parameters of the spectrum of a stationary non-deterministic time series,” Journal of the Australian Mathematical Society vol. 4, pp. 363–384, 1964.

    Article  MATH  Google Scholar 

  • R. W. M. Wedderburn, “Quasi-likelihood functions, generalized linear models, and the Gauss-Newton method,” Biometrika vol. 61 pp. 439–447, 1974.

    MATH  MathSciNet  Google Scholar 

  • C. Z. Wei and J. Winnicki, “Some asymptotic results for the branching process with immigration,” Stochastic Processes and their Applications vol. 31 pp. 261–282, 1989.

    Article  MathSciNet  MATH  Google Scholar 

  • P. Whittle, “Estimation and information in stationary time series,” Arkiv fõr Matematik vol. 2 pp. 423–434, 1953.

    MATH  MathSciNet  Google Scholar 

  • P. Whittle, “Some recent contributions to the theory of stationary processes.” In H. Wold (ed.), A Study in the Analysis of Stationary Time Series, Appendix 2 2nd ed. Almquist and Wiksell: Stockholm. pp. 196–228, 1954.

    Google Scholar 

  • J. Winnicki, “Estimation theory for the branching process with immigration,” Contemporary Mathematics vol. 80 pp. 301–322, 1988.

    MATH  MathSciNet  Google Scholar 

  • J. M. Wooldridge, “Estimation and inference for dependent processes.” In R. F. Engle and D. L. McFadden (eds.), Handbook of Econometrics, vol 4. pp. 2639–2738, Elsevier Science B. V.: North-Holland, Amsterdam, 1994.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Departamento de Matemática Aplicada, Faculdade de Ciências, Universidade do Porto, Rua do Campo Alegre, 687, 4169-007, Porto, Portugal

    Isabel Silva & M. Eduarda Silva

  2. Departamento de Matemática, Universidade de Aveiro, Aveiro, Portugal

    Isabel Pereira & Nélia Silva

  3. UI&D Matemática e Aplicações, Universidade de Aveiro, Aveiro, Portugal

    M. Eduarda Silva, Isabel Pereira & Nélia Silva

  4. Departamento de Engenharia Civil, Faculdade de Engenharia, Universidade do Porto, Porto, Portugal

    Isabel Silva

Authors
  1. Isabel Silva
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Eduarda Silva
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Isabel Pereira
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Nélia Silva
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. Eduarda Silva.

Additional information

AMS 2000 Subject Classification

62M10, 91B70, 60G10

Rights and permissions

Reprints and permissions

About this article

Cite this article

Silva, I., Silva, M.E., Pereira, I. et al. Replicated INAR(1) Processes. Methodol Comput Appl Probab 7, 517–542 (2005). https://doi.org/10.1007/s11009-005-5006-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11009-005-5006-x

Keywords

Search

Navigation