Decoupled-architecture-based nonlinear anti-windup design for a class of nonlinear systems

Abstract

This paper presents a comprehensive study on a dynamic nonlinear anti-windup compensator (AWC) design for nonlinear systems. It is shown that for asymptotically stable nonlinear systems, a full-order internal model control (IMC)-based AWC always exists regardless of the nonlinearity type. An alternative decoupled-architecture-based AWC offering better performance is proposed, wherein the selection of a nonlinear dynamical component plays a key role in establishing an equivalent decoupled architecture. Using the decoupled architecture, a quadratic Lyapunov function, the Lipschitz condition, the sector condition, and L ₂ gain reduction, a linear matrix inequality (LMI)-based AWC scheme is developed for systems with global Lipschitz nonlinearities. And by means of the local sector condition, a decoupled-architecture-based local AWC scheme (utilizing LMIs) for unstable and chaotic systems, which simultaneously guarantees a region of stability and the closed-loop performance for tracking-control applications, is derived. Simulation results establishing the effectiveness of the proposed AWC schemes are provided.

Appendices

Appendix A: AWC parameterization for complex nonlinear systems

Consider a general nonlinear system given by

(A.1)

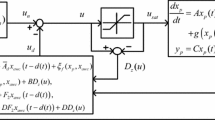
where the functions $g(x_{p},u_{\operatorname {sat}}) \in R^{n}$ and $l(x_{p},u_{\operatorname {sat}}) \in R^{p}$ represent time-varying nonlinearities. The decoupled-architecture-based AWC parameterization is given by

(A.2)

where F∈R ^m×n and h(x _p ,x _aw)∈R ^m are the unknown components of the AWC that can be selected to achieve the desired AWC performance. This parameterization is determined in the same way as described in Sect. 4. The corresponding IMC-based AWC can be obtained by Fx _aw+h(x _p ,x _aw)=0, which always exists for an asymptotically stable system (A.1).

Appendix B: Nonlinear matrix inequality-based AWC design

Consider the AWC parameterization, for a nonlinear system (1), given by

(B.1)

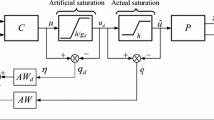
where nonlinearity h(x _p ,x _aw)∈R ^m represents a time-varying vector. By replacing Fx _aw with Fx _aw+h(x _p ,x _aw) in Figs. 2 and 3, a full-order AWC architecture and its equivalent decoupled architecture can be obtained for this parameterization. To design an AWC for a nonlinear system (1) using the parameterization (B.1), consider a Lyapunov function

$$ V = \gamma \bar{V}(x_{\mathrm{aw}}) > 0,\quad \bar{V}(x_{\mathrm{aw}}) > 0, \ \gamma > 0, $$

(B.2)

where γ is a constant and $\bar{V}(x_{\mathrm{aw}}) \in R$ is any positive definite function; for example, the extended quadratic Lyapunov function provided in [22].

Theorem B.1

Consider an overall closed-loop system, formed by plant (1), controller (3) and AWC (B.1), satisfies Assumption 1. Suppose there exists a matrix F∈R ^m×n and a function h(x _p ,x _aw)∈R ^m. Consider the optimization problem

$$\min \gamma $$

such that

$$ \gamma > 0,\qquad \bar{V}(x_{\mathrm{aw}}) > 0,\qquad U > 0, $$

(B.3)

(B.4)

where

(B.5)

(B.6)

γ is a scalar, and matrix U∈R ^m×m is a diagonal. The, the following holds:

• (i) There exists an AWC for an asymptotically stable plant (1) that ensures stability and windup prevention for the overall closed-loop system.

• (ii) The decoupled nonlinear part from u _n to y _d is asymptotically stable if u _n =0.

• (iii) The L ₂ gain from u _n to y _d is less than γ if u _n ≠0.

Proof

If Fx _aw+h(x _p ,x _aw)=0, then the AWC parameterization (B.1) becomes the same as the IMC-based AWC; hence, (i) is easily followed. The inequality (17) ensures (ii) and (iii). For Lyapunov function (B.2), the inequality (17) for AWC parameterization (B.1) gives $J_{1} = \bar{Z}^{T}\varPi _{3}\bar{Z} < 0$, where

$$ \bar{Z} = \left [ \begin{array}{c@{\quad}c@{\quad}c} I & \tilde{u}^{T} & u_{n}^{T} \end{array} \right ]^{T}, $$

(B.7)

$$ \varPi _{3} = \left [ \begin{array}{c@{\quad}c@{\quad}c} X_{1} + \gamma ^{ - 1}X_{2} + \gamma ^{ - 1}x_{\mathrm{aw}}^{T}\bar{C}{}^{T}\bar{C}x_{\mathrm{aw}} & \frac{1}{2} ( \frac{\partial \bar{V}}{\partial x_{\mathrm{aw}}} )B + \gamma ^{ - 1} ( x_{\mathrm{aw}}^{T}\bar{C}{}^{T}D + h(x_{p},x_{\mathrm{aw}})^{T}D^{T}D ) & 0 \\ * & \gamma ^{ - 1}D^{T}D & 0 \\ * & * & - \gamma I \end{array} \right ] < 0. $$

(B.8)

Sector condition (4) can be written as $\bar{Z}^{T}\varPi _{4}\bar{Z} \ge 0$, where

$$ \varPi _{4} = \left [ \begin{array}{c@{\quad}c@{\quad}c} 0 & - x_{\mathrm{aw}}^{T}F^{T}W - h(x_{p},x_{\mathrm{aw}})^{T}W & 0 \\ * & - 2W & W \\ * & * & 0 \end{array} \right ] \ge 0. $$

(B.9)

Combining (B8) and (B9) through the S-procedure (Π=Π ₃+εΠ ₄<0 with ε>0), taking v=εW and further applying the Schur complement followed by the congruence transform with $\operatorname {diag}(I,v^{ - 1},I,I)$, and taking v ⁻¹=U>0, (B.3)–(B.6) are obtained. This completes the proof of Theorem B.1. □

The results proposed in Theorem B.1 can be extended for oscillatory, unstable and chaotic locally Lipschitz and non-Lipschitz nonlinear systems by using the local sector condition. Due to its importance in nonlinear science, the final nonlinear matrix inequalities, by using the local sector condition (25)–(26) with u=u _n −Fx _aw−h(x _p ,x _aw) and w=u _n +Gx _aw−h(x _p ,x _aw), are given by

(B.10)

(B.11)

(B.12)

which can be used for the local AWC design of a nonlinear system (1) not verifying Assumption 2. These matrix inequalities are derived by utilizing the similar steps as was followed for the proofs of Theorems 2 and B.1.