Skip to main content
SpringerLink
Log in

Integrated guidance and control for reusable launch vehicle in reentry phase

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

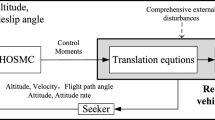
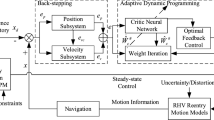
An integrated guidance and control scheme is developed for next generation of reusable launch vehicle (RLV) with the aim to improve the flexibility, safety and autonomy. Firstly, an outer-loop optimal feedback reentry guidance law with online trajectory reshaping capability is designed. Then, a novel reentry attitude control strategy is proposed based on multivariables smooth second-order sliding mode controller and disturbance observer. The proposed control scheme is able to guarantee that the guidance commands generated from the guidance system can be tracked in finite time. Furthermore, a control allocation is integrated in the system in order to transform the control moments to control surface deflection. Finally, some representative simulation tests are conducted to demonstrate the effectiveness of the proposed integrated guidance and control strategy for six-degree-of-freedom RLV.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Fahroo, F., Doman, D.: A direct method for approach and landing trajectory reshaping with failure effect estimation. In: AIAA Guidance, Navigation and Control Conference, AIAA-2004-4772 (2004)

  2. Alexandre, F., David, H., Ali, Z.: Robust fault diagnosis for atmospheric reentry vehicles: a case study. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 40(5), 886–899 (2010)

    Article  Google Scholar 

  3. Morio, V., Cazaurang, F., Zolghadri, A., et al.: Onboard path planning for reusable launch vehicles application to the shuttle orbiter reentry mission. Int. Rev. Aerosp. Eng. 1(6), 492–503 (2008)

    Google Scholar 

  4. Jiang, Z.S., Ardonez, R.: On-line robust trajectory generation on approach and landing for reusable launch vehicles. Automatica 45(7), 634–646 (2009)

    Article  Google Scholar 

  5. Gao, Y.: Linear feedback guidance for low-thrust many-revolution earth-orbit transfers. J. Spacecr. Rockets 46(6), 1320–1325 (2010)

    Article  Google Scholar 

  6. Tian, B.L., Zong, Q.: Optimal guidance for reentry vehicles based on indirect Legendre pseudospectral method. Acta Astronaut. 68(7–8), 1176–1184 (2011)

    Article  Google Scholar 

  7. Mease, K.D., Kremer, J.P.: Shuttle entry guidance revisited using nonlinear geometric methods. J. Guid. Control Dyn. 17(6), 1350–1356 (1994)

    Article  Google Scholar 

  8. Harpold, J.C., Graves, C.A.: Shuttle Program: Shuttle Entry Guidance; NASA-TM-79949 (1979)

  9. Bogner, I.: Description of Apollo Entry Guidance. Technical memorandum, NASA (1966)

  10. Braun, R.D., Powell, R.W.: Predictor–corrector guidance algorithm for use in high-energy aerobraking system studies. J. Guid. Control Dyn. 15(3), 672–678 (1992)

    Article  Google Scholar 

  11. Mease, K.D., Chen, D.T., Tandon, S., et al.: A Three-Dimensional Predictive Entry Guidance Approach. AIAA Paper 2000-3959 (2000)

  12. Zimmerman, C., Dukeman, G., Hanson, J.: Automated method to compute orbital reentry trajectories with heating constraints. J. Guid. Control Dyn. 26(4), 523–529 (2003)

    Article  Google Scholar 

  13. Xue, S.B., Lu, P.: Constrained predictor–corrector entry guidance. J. Guid. Control Dyn. 33(4), 1273–1281 (2010)

    Article  Google Scholar 

  14. Padhi, R., Kothari, M.: Model predictive static programming: a computationally efficient technique for suboptimal control design. Int. J. Innov. Comput. Inf. Control 5(2), 399–411 (2009)

    Google Scholar 

  15. Chawla, c, Sarmah, P., Padhi, R.: Suboptimal reentry guidance of reusable launch vehicles using pitch plane maneuver. Aerosp. Sci. Technol. 14(6), 377–386 (2010)

    Article  Google Scholar 

  16. Dwived, P.N., Bhattacharya, A., Padhi, R.: Suboptimal midcourse guidance of interceptors for high speed targets with alignment angle constraint. J. Guid. Control Dyn. 34(3), 860–877 (2011)

    Article  Google Scholar 

  17. Halbe, O., Raja, R.G., Padhi, R.: Robust reentry guidance of a reusable launch vehicle using model predictive static programming. J. Guid. Control Dyn. 37(1), 134–148 (2011)

    Article  Google Scholar 

  18. Ross, I.M., Karpenko, M.: A review of pseudospectral optimal control: from theory to flight. Annu. Rev. Control 36(2), 182–197 (2012)

    Article  Google Scholar 

  19. Darby, C.L., Hager, W.W., Rao, A.V.: Direct trajectory optimization using a variable low-order adaptive pseudospectral method. J. Spacecr. Rockets 48(3), 433–455 (2011)

    Article  Google Scholar 

  20. Zong, Q., Tian, B.L., Dou, L.Q., et al.: Ascent phase trajectory optimization for vehicle with space restricted. Trans. Jpn. Soc. Aeronaut. Space Sci. 54(183), 37–43 (2011)

    Article  Google Scholar 

  21. Benson, D.A., Huntington, G.T., Thorvaldsen, T.P.: Direct trajectory optimization and costate estimation via an orthogonal collocation method. J. Guid. Control Dyn. 29(6), 1435–1440 (2006)

    Article  Google Scholar 

  22. Hodel, A.S., Hall, C.E.: Variable-structure PID control to prevent integrator windup. IEEE Trans. Ind. Electron. 48(2), 442–451 (2001)

    Article  Google Scholar 

  23. Smith, R., Ahmed, A., Hadaegh, F.Y.: The design of a robust parametrically varying attitude controller for the X-33 vehicle. In: AIAA Guidance, Navigation, and Control Conference and Exhibit, Denver, CO, 14–17 August 2000, paper no. AIAA-2000-4158 (2000)

  24. Lian, B.H., Bang, H.C., Hurtado, J.E.: Adaptive backstepping control based autopilot design for reentry vehicles. In: AIAA Guidance, Navigation, and Control Conference, Providence, Rhode Island, 16–19 August 2004, paper no. AIAA-2004-5328 (2004)

  25. Farrell, J., Sharma, M., Polycarpou, M.: Backstepping-based flight control with adaptive function approximation. J. Guid. Control Dyn. 28(6), 1089–1102 (2005)

    Article  Google Scholar 

  26. Zhu, J.J., Hodel, A., Scott, A,. et al.: X-33 entry flight controller design by trajectory linearization-a singular perturbational approach. In: American Astronautical Society Guidance and Control Conference, Breckenridge, CO, January 31–February 4 2001, pp. 151–170 (2001)

  27. Bevaqua, T., Best, E., Huizenga, A., et al.: Improved trajectory linearization flight controller for reusable launch vehicles. In: AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada. 5–8 January 11 2004, paper no. AIAA-2004-875 (2004)

  28. Georgie, J., Valasek, J.: Evaluation of longitudinal desired dynamics for dynamic Inversion controlled generic re-entry vehicles. J. Guid. Control Dyn. 26(5), 811–819 (2003)

    Article  Google Scholar 

  29. Ito, D., Ward, D.T., Valasek, J.: Robust dynamic inversion controller design and analysis for the X-38. In: AIAA Conference on Guidance, Navigation and Control, Canada, 6–9 August, 2001, paper no. AIAA-2001-4380 (2001)

  30. Huang, J., Sun, L.N., Han, Z.Z., et al.: Adaptive terminal sliding mode control for nonlinear differential inclusion systems with disturbance. Nonlinear Dyn. 72(1–2), 221–228 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  31. Sun, H.B., Li, S.H., Sun, C.Y.: Finite time integral sliding mode control of hypersonic vehicles. Nonlinear Dyn. 73(1–2), 229–244 (2013)

    Article  MATH  Google Scholar 

  32. Gao, G., Wang, J.Z.: Observer-based fault-tolerant control for an air-breathing hypersonic vehicle model. Nonlinear Dyn. 76(1), 409–430 (2014)

    Article  Google Scholar 

  33. Niu, Y.J., Wang, X.Y.: A novel adaptive fuzzy sliding-mode controller for uncertain chaotic systems. Nonlinear Dyn. 73(3), 1201–1209 (2013)

    Article  MathSciNet  Google Scholar 

  34. Zhang, Y.X., Sun, M.W., Chen, Z.Q.: Finite-time convergent guidance law with impact angle constraint based on sliding-mode control. Nonlinear Dyn. 70(1), 619–625 (2012)

    Article  MathSciNet  Google Scholar 

  35. Shtessel, Y.B., Hall, C.E., Jackson, M.: Reusable launch vehicle control in multiple-time-scale sliding modes. J. Guid. Control Dyn. 23(6), 1013–1020 (2000)

    Article  Google Scholar 

  36. Shtessel, Y.B., Hall, C.E.: Multiple time scale sliding mode control of reusable launch vehicles in ascent and descent modes. In: American Control Conference, Piscataway, NJ 2001, pp. 4357–4362 (2001)

  37. Massey, T., Shtessel, Y.B.: Continuous traditional and high-order sliding modes for satellite formation control. J. Guid. Control Dyn. 28(4), 826–831 (2005)

    Article  Google Scholar 

  38. Hall, C.E., Shtessel, Y.B.: Sliding mode disturbance observer-based control for a reusable launch vehicle. J. Guid. Control Dyn. 29(6), 1315–1328 (2006)

    Article  Google Scholar 

  39. Stott, J.E., Shtessel, Y.B.: Launch vehicle attitude control using sliding mode control and observation techniques. J. Frankl. Inst. 349(2), 397–412 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  40. Besnard, L., Shtessel, Y.B., Landrum, B.: Quadrotor vehicle control via sliding mode controller driven by sliding mode disturbance observer. J. Frankl. Inst. 349(2), 658–684 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  41. Nagesh, I., Edwards, C.: A multivariable super-twisting sliding mode approach. Automatica 50(3), 984–988 (2014)

    Article  MATH  MathSciNet  Google Scholar 

  42. Bollino, K., Ross, I.M., Doman, D.: Optimal nonlinear feedback guidance for reentry vehicle. In: AIAA Guidance, Navigation and Control Conference, Keystone Co, AIAA 2006-6074 (2006)

  43. Darby, C.L., Hager, W.W., Rao, A.V.: An hp-adaptive pseudospectral method for solving optimal control problems. Optim. Control Appl. Methods 32(4), 476–502 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  44. Tian, B.L., Zong, Q.: 3DOF ascent phase trajectory optimization for aircraft based on adaptive Gauss pseudospectral method. 2012 Third International Conference on Intelligent Control and Information Processing, Dalian, China, July 15–17, 2012, pp. 431–435 (2012)

  45. Ross, I.M., Sekhavat, P., Fleming, A.: Optimal feedback control: foundations, examples and experimental results for a new approach. J. Guid. Control Dyn. 31(2), 307–321 (2008)

    Article  Google Scholar 

  46. Bollino, K.P.: High fidelity real-time trajectory optimization for reusable launch vehicles. Ph.D Thesis, Naval Postgraduate School (2006)

  47. Bhat, S.P., Bernstein, D.S.: Finite-time stability of continuous autonomous systems. SIAM J. Control Optim. 38(3), 751–766 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  48. Moreno, J.A., Osorio, M.: Strict Lyapunov functions for the super-twisting algorithm. IEEE Trans. Autom. Control 57(4), 1035–1040 (2012)

    Article  MathSciNet  Google Scholar 

  49. Khalil, H.K.: Nonlinear System, 3rd edn. Prentice Hall, Englewood Cliffs (2001)

    Google Scholar 

  50. Recasens, J.J., Chu, Q.P., Mulder, J.A.: Robust model predictive control of a feedback linearized system for a lifting-body reentry vehicle. In: AIAA Guidance, Navigation, and Control Conference and Exhibit, San Francisco, California, AIAA-2005-6147 (2005)

  51. Estrada, A., Loria, A., Santiesteban, R., et al.: Cascaded-based stabilization of time-varying systems using 2nd-order sliding modes. IMA J. Math. Control Inf. 30(1), 115–128 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  52. Shkolnikov, I.A., Shtessel, Y.B.: A multiple loop sliding mode control system with second-order boundary layer dynamics. In: 15th World Congress of the International Federation of Automatic Control, Barcelona (2002)

  53. Shtessel, Y.B., Shkolnikov, I.A., Levant, A.: Smooth second-order sliding modes: missile guidance application. Automatica 43, 1470–1476 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  54. Harkegard, O., Glad, S.T.: Resolving actuator redundancy-optimal control vs control allocation. Automatica 41(1), 137–144 (2005)

    MathSciNet  Google Scholar 

  55. Harkegard, O.: Efficient active set algorithms for solving constrained least squares problems in aircraft control allocation. In: Proceedings of the 41st IEEE Conference on Decision and Control. Las Vegas, NV, pp. 1295–1300 (2002)

Download references

Acknowledgments

This work has been supported by National Natural Science Foundation of China (61203012, 61304018, 61273092), Key Grant Project of Chinese Ministry of Education (311012) and Tianjin Research Program of Application Foundation and Advanced Technology (12JCZDJC30300). Independent Innovation Fund of Tianjin University (2013XQ-0022),.

Author information

Authors and Affiliations

  1. School of Electric and Automation Engineering, Tianjin University, Tianjin, 300072, China

    Bailing Tian & Qun Zong

  2. Aeronautical Automation College, Civil Aviation University of China, Tianjin, 300300, China

    Wenru Fan

Authors
  1. Bailing Tian
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Wenru Fan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Qun Zong
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Bailing Tian.

Appendix: Proof of Theorem 1

Appendix: Proof of Theorem 1

Proof

For brevity, we present system (16) in a form convenient for Lyapunov analysis. To this end, a new state vector is introduced

$$\begin{aligned} \mathbf{z}_1 =\left\| {\mathbf{x}_1 } \right\| ^{p-1}\mathbf{x}_1 ,\quad \mathbf{z}_2 =\mathbf{x}_2 \end{aligned}$$
(36)

Furthermore, system (16) can be rewritten as

$$\begin{aligned} \dot{\mathbf{z}}_1&= \left( {\mathbf{I}_m +\left( {p-1} \right) \frac{\mathbf{x}_1 \mathbf{x}_1 ^{T}}{\left\| {\mathbf{x}_1 } \right\| ^{2}}} \right) \left\| {\mathbf{x}_1 } \right\| ^{\left( {p-1} \right) }\dot{\mathbf{x}}_1,\nonumber \\ \dot{\mathbf{z}}_2&= -k_2 p\left\| {\mathbf{x}_1 } \right\| ^{p-1}\mathbf{z}_1 +\varvec{\Delta }_2 \end{aligned}$$
(37)

where \(\mathbf{I}_m \) denotes m-dimensional unit matrix. Taking into account the definition in (36), we obtain \(\left\| {\mathbf{z}_1 } \right\| =\left\| {\mathbf{x}_1 } \right\| ^{p}\) and \(\mathbf{x}_1 =\mathbf{z}_1 /\left\| {\mathbf{x}_1 } \right\| ^{p-1}=\mathbf{z}_1 /\left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\). Therefore, system (37) can be equivalently written as

$$\begin{aligned} \dot{\mathbf{z}}_1&= \left( {\mathbf{I}_m +\left( {p-1} \right) \frac{\mathbf{z}_1 \mathbf{z}_1 ^{T}}{\left\| {\mathbf{z}_1 } \right\| ^{2}}} \right) \left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\nonumber \\&\times \left( {-k_1 \mathbf{z}_1 +\mathbf{z}_2 +\varvec{\Delta }_1 } \right) ,\nonumber \\ \dot{\mathbf{z}}_2&= -k_2 p\left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\mathbf{z}_1 +\varvec{\Delta }_2 \end{aligned}$$
(38)

It follows from the definition in (36) that \(\mathbf{z}_1,\,\mathbf{z}_2 \rightarrow 0\) in finite time implies that \(\mathbf{x}_1,\,\mathbf{x}_2 \rightarrow 0\) in finite time. Next, a Lyapunov function candidate is proposed as

$$\begin{aligned} V\left( {\mathbf{z}_1,\mathbf{z}_2 } \right) =\left( {k_2 +\frac{1}{2}k_1^2 } \right) \mathbf{z}_1^T \mathbf{z}_1 +\mathbf{z}_2^T \mathbf{z}_2 -k_1 \mathbf{z}_1^T \mathbf{z}_2\nonumber \\ \end{aligned}$$
(39)

It is easy to verify that \(V\left( {\mathbf{z}_1,\mathbf{z}_2 } \right) \) is positive definite and radially unbounded for arbitrary positive constants \(k_1 >0\,\hbox {and}\,k_2 >0\). The derivative of \(V\left( {\mathbf{z}_1,\mathbf{z}_2 } \right) \) is given by

$$\begin{aligned} \dot{V}\left( {\mathbf{z}_1,\mathbf{z}_2 } \right)&= \left( {2k_2 +k_1^2 } \right) \mathbf{z}_1^T \dot{\mathbf{z}}_1 +2\mathbf{z}_2^T \dot{\mathbf{z}}_2\nonumber \\&\quad -\,k_1 \left( {\dot{\mathbf{z}}_1^T \mathbf{z}_2 +\mathbf{z}_1^T \dot{\mathbf{z}}_2 } \right) \end{aligned}$$
(40)

Substituting (38) into (40) yields

$$\begin{aligned}&V=\left( {2k_2 +k_1^2 } \right) \mathbf{z}_1^T \left[ \left( {\mathbf{I}_m +\left( {p-1} \right) \frac{\mathbf{z}_1 \mathbf{z}_1 ^{T}}{\left\| {\mathbf{z}_1 } \right\| ^{2}}} \right) \left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\right. \nonumber \\&\left. \quad \times \left( {-k_1 \mathbf{z}_1 +\mathbf{z}_2 +\varvec{\Delta }_1 } \right) \right] +2\mathbf{z}_2^T \left( {-k_2 p\left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\mathbf{z}_1 +\varvec{\Delta }_2 } \right) \nonumber \\&\quad -\,k_1 \left[ \left( {\mathbf{I}_m +\left( {p-1} \right) \frac{\mathbf{z}_1 \mathbf{z}_1 ^{T}}{\left\| {\mathbf{z}_1 } \right\| ^{2}}} \right) \left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\right. \nonumber \\&\qquad \left. \left( {-k_1 \mathbf{z}_1 +\mathbf{z}_2 +\varvec{\Delta }_1 } \right) \right] ^{T}\mathbf{z}_2 \nonumber \\&\quad -\,k_1 \mathbf{z}_1^T \left( {-k_2 p\left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\mathbf{z}_1 +\varvec{\Delta }_2 } \right) \nonumber \\&\quad =\left( {2k_2 +k_1^2 } \right) p\left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\left( {-k_1 \left\| {\mathbf{z}_1 } \right\| ^{2}+\mathbf{z}_1^T \mathbf{z}_2 +\mathbf{z}_1^T \varvec{\Delta }_1 } \right) \nonumber \\&\quad -\,2k_2 p\left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\mathbf{z}_1^T \mathbf{z}_2 +2\mathbf{z}_2^T \varvec{\Delta }_2 +k_1 \left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\nonumber \\&\quad \left[ {\left( {k_1 \mathbf{z}_1^T -\mathbf{z}_2^T -\varvec{\Delta }_1^T } \right) \left( {\mathbf{I}_m +\left( {p-1} \right) \frac{\mathbf{z}_1 \mathbf{z}_1^T }{\left\| {\mathbf{z}_1 } \right\| ^{2}}} \right) \mathbf{z}_2 } \right] \nonumber \\&\quad +\,k_1 \mathbf{z}_1 ^{T}\left[ {k_2 p\left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\mathbf{z}_1 -\varvec{\Delta }_2 } \right] \nonumber \\&\quad =\left( {2k_2 +k_1^2 } \right) p\left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\left( {-k_1 \left\| {\mathbf{z}_1 } \right\| ^{2}+\mathbf{z}_1^T \mathbf{z}_2 +\mathbf{z}_1^T \varvec{\Delta }_1 } \right) \nonumber \\&\quad -\,2k_2 p\left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\mathbf{z}_1^T \mathbf{z}_2 +2\mathbf{z}_2^T \varvec{\Delta }_2 +k_1 \left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\nonumber \\&\quad \left[ k_1 p\mathbf{z}_1^T \mathbf{z}_2 -\left( {\left\| {\mathbf{z}_2 } \right\| ^{2}+\left( {p-1} \right) \frac{\left( {\mathbf{z}_2^T \mathbf{z}_1 } \right) \left( {\mathbf{z}_1^T \mathbf{z}_2 } \right) }{\left\| {\mathbf{z}_1 } \right\| ^{2}}} \right) \right. \nonumber \\&\left. \quad -\varvec{\Delta }_1^T \left( {\mathbf{I}_m +\left( {p-1} \right) \frac{\mathbf{z}_1 \mathbf{z}_1^T }{\left\| {\mathbf{z}_1 } \right\| ^{2}}} \right) \mathbf{z}_2\right] \nonumber \\&\quad +\,k_1 k_2 p\left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\left\| {\mathbf{z}_1 } \right\| ^{2}-k_1 \mathbf{z}_1^T \varvec{\Delta }_2 \nonumber \\&\quad =\left[ -\left( {k_2 +k_1^2 } \right) k_1 p\left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\left\| {\mathbf{z}_1 } \right\| ^{2}\right. \nonumber \\&\quad \left. +\,2k_1^2 p\left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\mathbf{z}_1^T \mathbf{z}_2-\,k_1 \left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\right. \nonumber \\&\quad \left. \left( {\left\| {\mathbf{z}_2 } \right\| ^{2}+\left( {p-1} \right) \frac{\left( {\mathbf{z}_2^T \mathbf{z}_1 } \right) \left( {\mathbf{z}_1^T \mathbf{z}_2 } \right) }{\left\| {\mathbf{z}_1 } \right\| ^{2}}} \right) \right] \nonumber \\&\quad +\,\left[ -k_1 \left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\left( {\varvec{\Delta }_1^T \mathbf{z}_2 +\left( {p-1} \right) \frac{\left( {\Delta _1^T \mathbf{z}_1 } \right) \left( {\mathbf{z}_1^T \mathbf{z}_2 } \right) }{\left\| {\mathbf{z}_1 } \right\| ^{2}}} \right) \right. \nonumber \\&\quad \left. +\,2\mathbf{z}_2^T \varvec{\Delta }_2 -k_1 \mathbf{z}_1^T \varvec{\Delta }_2 \right. \nonumber \\&\quad +\,\left. {\left( {2k_2 +k_1^2 } \right) p\left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\mathbf{z}_1^T \varvec{\Delta }_1 } \right] \nonumber \\&\quad =\left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\left[ -\left( {k_2 +k_1^2 } \right) k_1 p\left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\left\| {\mathbf{z}_1 } \right\| ^{2}\right. \nonumber \\&\quad \left. +\,2k_1^2 p\left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\mathbf{z}_1^T \mathbf{z}_2 -k_1 \left\| {\mathbf{z}_2 } \right\| ^{2}\right. \nonumber \\&\quad \left. +k_1 \left( {1-p} \right) \frac{\left( {\mathbf{z}_2^T \mathbf{z}_1 } \right) \left( {\mathbf{z}_1^T \mathbf{z}_2 } \right) }{\left\| {\mathbf{z}_1 } \right\| ^{2}} \right] \nonumber \end{aligned}$$
$$\begin{aligned}&\quad +\,\left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\left[ \left( {2k_2 +k_1^2 } \right) p\mathbf{z}_1^T \varvec{\Delta }_1 -k_1 \mathbf{z}_1^T \varvec{\Delta }_2\right. \nonumber \\&\quad \left. +\,k_1 \left( {1-p} \right) \frac{\left( {\Delta _1^T \mathbf{z}_1 } \right) \left( {\mathbf{z}_1^T \mathbf{z}_2 } \right) }{\left\| {\mathbf{z}_1 } \right\| ^{2}} \right] \nonumber \\&\quad +\,\left( {2\mathbf{z}_2 -k_1 \mathbf{z}_2 } \right) ^{T}\varvec{\Delta }_2 \end{aligned}$$
(41)

Taking into account \(p\in \left( {0.5,1} \right) \) and using Cauchy–Schwarz inequality on the inner product terms, we have

$$\begin{aligned} V&\le \left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\left[ -\left( {k_2 +k_1^2 } \right) k_1 p\left\| {\mathbf{z}_1 } \right\| ^{2}+2k_1^2 p\left\| {\mathbf{z}_1 } \right\| \right. \nonumber \\&\left. \quad \times \left\| {\mathbf{z}_2 } \right\| -\,k_1\left\| {\mathbf{z}_2 } \right\| ^{2}+k_1 \left( {1-p} \right) \left\| {\mathbf{z}_2 } \right\| ^{2}\right] \nonumber \\&\quad +\,\left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\left[ \left( {2k_2 +k_1^2 } \right) p\left\| {\mathbf{z}_1 } \right\| \left\| {\varvec{\Delta }_1 } \right\| \right. \nonumber \\&\left. \quad +\,k_1 \left\| {\varvec{\Delta }_1 } \right\| \left\| {\mathbf{z}_2 } \right\| +k_1 \left( {1-p} \right) \left\| {\varvec{\Delta }_1 } \right\| \left\| {\mathbf{z}_2 } \right\| \right] \nonumber \\&\quad +\,\left\| {\left( {2\mathbf{z}_2 -k_1 \mathbf{z}_2 } \right) } \right\| \left\| {\varvec{\Delta }_2 } \right\| \nonumber \\&\le p\left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\left[ -\left( {k_2 +k_1^2 } \right) k_1 \left\| {\mathbf{z}_1 } \right\| ^{2}\right. \nonumber \\&\left. \quad +\,2k_1^2 \left\| {\mathbf{z}_1 } \right\| \left\| {\mathbf{z}_2 } \right\| -k_1 \left\| {\mathbf{z}_2 } \right\| ^{2} \right] \nonumber \\&\quad +\,\left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\left[ \left( {2k_2 +k_1^2 } \right) p\left\| {\mathbf{z}_1 } \right\| \right. \nonumber \\&\left. \quad +\,\left( {2k_1 -k_1 p}\right) \left\| {\mathbf{z}_2 } \right\| \right] \left\| {\varvec{\Delta }_1 } \right\| \nonumber \\&\quad +\,\sqrt{4+k_1^2 }\sqrt{\left\| {\mathbf{z}_1 } \right\| ^{2}+\left\| {\mathbf{z}_2 } \right\| ^{2}}\left\| {\varvec{\Delta }_2 } \right\| \nonumber \\&\le -p\left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\left[ \left( {k_2 +k_1^2 } \right) k_1 \left\| {\mathbf{z}_1 } \right\| ^{2}-2k_1^2 \right. \nonumber \\&\left. \quad \,\left\| {\mathbf{z}_1 } \right\| \left\| {\mathbf{z}_2 } \right\| +k_1 \left\| {\mathbf{z}_2 } \right\| ^{2} \right] \nonumber \\&\quad +\,\left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\sqrt{\left( {2k_2 +k_1^2 } \right) ^{2}p^{2}+\left( {2k_1 -k_1 p} \right) ^{2}}\nonumber \\&\quad \,\sqrt{\left\| {\mathbf{z}_1 } \right\| ^{2}+\left\| {\mathbf{z}_2 } \right\| ^{2}}\left\| {\varvec{\Delta }_1 } \right\| \nonumber \\&\quad +\,\sqrt{4+k_1^2 }\sqrt{\left\| {\mathbf{z}_1 } \right\| ^{2}+\left\| {\mathbf{z}_2 } \right\| ^{2}}\left\| {\varvec{\Delta }_2 } \right\| \end{aligned}$$
(42)

Let \(\mathbf{z}=\left[ {\left\| {\mathbf{z}_1 } \right\| \,\left\| {\mathbf{z}_2 } \right\| } \right] ^{T}\), it is obvious that the first item on the right-hand side of (42) can be rewritten as \(-p\left\| {\mathbf{z}_\mathbf{1} } \right\| ^{\frac{p-1}{p}}\mathbf{z}^{T}\mathbf{Qz}\) with positive definite matrix \(\mathbf{Q}=\left[ {{\begin{array}{ll} {\left( {k_2 +k_1^2 } \right) k_1 }&{} {-k_1^2 } \\ {-k_1^2 }&{} {k_1 } \\ \end{array} }} \right] \) for any positive constants \(k_1 >0\,\hbox {and}\,k_2 >0\). In addition, it is easily verified that \(\lambda _\mathrm{mim} \left( \mathbf{Q} \right) \left\| \mathbf{z} \right\| ^{2}\le \mathbf{z}^{T}\mathbf{Qz}\le \lambda _{\max } \left( \mathbf{Q} \right) \left\| \mathbf{z} \right\| ^{2}\) with \(\lambda _\mathrm{mim} \left( \mathbf{Q} \right) \) and \(\lambda _{\max } \left( \mathbf{Q} \right) \) being the minimum and maximum eigenvalue of matrix \(\mathbf{Q}\), respectively. Furthermore, in view of bounds on the terms \(\left\| {\varvec{\Delta }_1 } \right\| \) and\(\left\| {\varvec{\Delta }_2 } \right\| \), we have

$$\begin{aligned} \dot{V}&\le -p\left\| {\mathbf{z}_\mathbf{1} } \right\| ^{\frac{p-1}{p}}\lambda _{\min } \left( \mathbf{Q} \right) \left\| \mathbf{z} \right\| ^{2}\nonumber \\&\quad +\,\left\| {\mathbf{z}_\mathbf{1} } \right\| ^{\frac{p-1}{p}}\sqrt{\left( {2k_2 +k_1^2 } \right) ^{2}p^{2}+\left( {2k_1 -k_1 p} \right) ^{2}}\nonumber \\&\quad \times \left\| \mathbf{z} \right\| \delta _1+\,\sqrt{4+k_1^2 }\left\| \mathbf{z} \right\| \delta _2 \end{aligned}$$
(43)

Next, we want to use part of \(-p\left\| {\mathbf{z}_\mathbf{1} } \right\| ^{\frac{p-1}{p}}\lambda _{mim} \left( \mathbf{Q} \right) \left\| \mathbf{z} \right\| ^{2}\) to dominate the last two items on the right-hand side of (43) for large \(\left\| \mathbf{z} \right\| \). To this end, we rewrite the inequality (43) as

$$\begin{aligned} \dot{V}&\le -p\left( {1-\theta _1 -\theta _2 } \right) \left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\lambda _{\min } \left( \mathbf{Q} \right) \left\| \mathbf{z} \right\| ^{2}\nonumber \\&\quad +\,\left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\left( \sqrt{\left( {2k_2 +k_1^2 } \right) ^{2}p^{2}+\left( {2k_1 -k_1 p} \right) ^{2}}\delta _1\right. \nonumber \\&\quad \left. -\,\theta _1 \lambda _{\min } \left( \mathbf{Q} \right) \left\| \mathbf{z} \right\| \right) \left\| \mathbf{z} \right\| \nonumber \\&\quad +\,\left( {\sqrt{4+k_1^2 }\delta _2 -\theta _2 \left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\lambda _{\min } \left( \mathbf{Q} \right) \left\| \mathbf{z} \right\| } \right) \left\| \mathbf{z} \right\| \nonumber \\ \end{aligned}$$
(44)

where \(\theta _1\,\hbox {and}\,\theta _2 \) are positive constants and satisfy \(0<\theta _1+\theta _2 <1\). Furthermore, let \(\mathbf{Z}=\left[ {\mathbf{z}_1;\,\mathbf{z}_2 } \right] \). It follows from the definition of Lyapunov function in (39) that it can be rewritten as \(V\left( {\mathbf{z}_1,\,\mathbf{z}_2 } \right) =\mathbf{Z}^{T}\mathbf{PZ}\) for an appropriate symmetric positive definite matrix \(\mathbf{P}\in R^{2m\times 2m}\). Therefore, the following inequality is satisfied for any vector \(\mathbf{Z}\)

$$\begin{aligned} \lambda _{\min } \left( \mathbf{P} \right) \left\| \mathbf{Z} \right\| ^{2}\le V\le \lambda _{\max } \left( \mathbf{P} \right) \left\| \mathbf{Z} \right\| ^{2} \end{aligned}$$
(45)

where \(\lambda _{\min } \left( \mathbf{P} \right) \) and \(\lambda _{\max } \left( \mathbf{P} \right) \) represent the minimum and maximum eigenvalue of matrix \(\mathbf{P}\), respectively. In addition, it can be observed from the definition of \(\mathbf{z}\,\hbox {and}\,\mathbf{Z}\) that \(\left\| {\mathbf{z}} \right\| =\left\| \mathbf{Z} \right\| \). Therefore, based on (45), we have inequality \(\frac{V^{1/2}}{\left[ {\lambda _{\mathrm{max}} \left( \mathbf{P} \right) } \right] ^{1/2}}\le \left\| \mathbf{z} \right\| =\left\| \mathbf{Z} \right\| =\le \frac{V^{1/2}}{\left[ {\lambda _{\min } \left( \mathbf{P} \right) } \right] ^{1/2}}\). Since \(0.5<p<1\), it can be concluded that \(\left\| {\mathbf{z}_\mathbf{1} } \right\| ^{\frac{p-1}{p}}\ge \left\| \mathbf{z} \right\| ^{\frac{p-1}{p}}\ge \frac{V^{\left( {p-1} \right) /\left( {2p} \right) }}{\left[ {\lambda _{\max } \left( \mathbf{P} \right) } \right] ^{\left( {p-1} \right) /\left( {2p} \right) }}\). Then, inequality (44) satisfies

$$\begin{aligned} \dot{V}&\le -p\left( {1-\theta _1 -\theta _2 } \right) \frac{\lambda _{\mathrm{min}} \left( \mathbf{Q} \right) }{\left[ {\lambda _{\max } \left( \mathbf{P} \right) } \right] \left[ {\lambda _{\min } \left( \mathbf{P} \right) } \right] ^{\left( {p-1} \right) /\left( {2p} \right) }}\nonumber \\&\quad \times V^{\left( {3p-1} \right) /\left( {2p} \right) }+\left\| {\mathbf{z}_1 } \right\| ^{\frac{p-1}{p}}\nonumber \\&\quad \times \left( \sqrt{\left( {2k_2 +k_1^2 } \right) ^{2}p^{2}+\left( {2k_1 -k_1 p} \right) ^{2}}\delta _1\right. \nonumber \\&\quad \quad \left. -\theta _1 \lambda _{\min } \left( \mathbf{Q} \right) \left\| \mathbf{z} \right\| \right) \left\| \mathbf{z}\right\| \nonumber \\&\quad +\,\left( {\sqrt{4+k_1^2 }\delta _2 -\theta _2 \lambda _{\min } \left( \mathbf{Q} \right) \left\| \mathbf{z} \right\| ^{\frac{2p-1}{p}}} \right) \left\| \mathbf{z} \right\| \nonumber \\ \end{aligned}$$
(46)

Then,

$$\begin{aligned}&\dot{V}\le -p\left( {1-\theta _1 -\theta _2 } \right) \frac{\lambda _{\mathrm{min}} \left( \mathbf{Q} \right) }{\left[ {\lambda _\mathrm{max} \left( \mathbf{P} \right) } \right] \left[ {\lambda _{\mathrm{min}} \left( \mathbf{P} \right) } \right] ^{\left( {p-1} \right) /\left( {2p} \right) }}V^{\left( {3p-1} \right) /\left( {2p} \right) },\forall \left\| \mathbf{z} \right\| \in \Xi _1 \nonumber \\&\quad =\left\{ {\left\| \mathbf{z} \right\| \ge \underbrace{\hbox {max}\left( {\frac{\sqrt{\left( {2k_2 +k_1^2 } \right) ^{2}p^{2}+\left( {2k_1 -k_1 p} \right) ^{2}}\delta _1 }{\theta _1 \lambda _{\mathrm{min}} \left( \mathbf{Q} \right) },\left( {\frac{\sqrt{4+k_1^2 }\delta _2 }{\theta _2 \lambda _{\mathrm{min}} \left( \mathbf{Q} \right) }} \right) ^{p/\left( {2p-1} \right) }} \right) }_\Upsilon } \right\} \end{aligned}$$
(47)

It follows from (47) and theorem 4.18 in [49] that the solution for [A3] is globally bounded. Furthermore, inequality (A8) is reduced to

$$\begin{aligned}&\dot{V}\le -p\left\| {\mathbf{z}_\mathbf{1} } \right\| ^{\frac{p-1}{p}}\lambda _{\min } \left( \mathbf{Q} \right) \left\| \mathbf{z} \right\| ^{2}\nonumber \\&\quad \le \frac{\lambda _{\min } \left( \mathbf{Q} \right) }{\left[ {\lambda _{\min } \left( \mathbf{P} \right) \lambda _{\min } \left( \mathbf{P} \right) } \right] ^{\frac{p-1}{2p}}}V^{\frac{3p-1}{2p}} \end{aligned}$$
(48)

if \(\varvec{\Delta }_1 =\varvec{\Delta }_2 =0\). It follows from \(0.5<p<1\) that we obtain \(\frac{3p-1}{2p}\in \left( {0.5,1} \right) \). According to Lemma 1, it can be concluded that \(\mathbf{z}_1 \), \(\mathbf{z}_2 \rightarrow 0\) in finite time. This completes the proof.\(\square \)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tian, B., Fan, W. & Zong, Q. Integrated guidance and control for reusable launch vehicle in reentry phase. Nonlinear Dyn 80, 397–412 (2015). https://doi.org/10.1007/s11071-014-1877-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-014-1877-0

Keywords

Search

Navigation