A four-wing hyper-chaotic attractor generated from a 4-D memristive system with a line equilibrium

Abstract

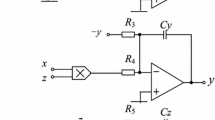
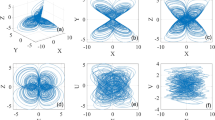
A new hyper-chaotic system is presented in this paper by adding a smooth flux-controlled memristor and a cross-product item into a three-dimensional autonomous chaotic system. It is exciting that this new memristive system can show a four-wing hyper-chaotic attractor with a line equilibrium. The dynamical behaviors of the proposed system are analyzed by Lyapunov exponents, bifurcation diagram and Poincaré maps. Then, by using the topological horseshoe theory and computer-assisted proof, the existence of hyperchaos in the system is verified theoretically. Finally, an electronic circuit is designed to implement the hyper-chaotic memristive system.

Appendices

Appendix 1. A theorem of topological horseshoe

Let $D$ be a compact region of ${R^q}$, and $D_i = 1,2,\ldots ,p$, be compact subsets of $D$. For each ${D_i}$, let $D_i^1$ and $D_i^2$ be its two fixed disjointed connected nonempty compact subsets contained in the boundary of $D_i$. Let $f:{D_i} \rightarrow {R^q}$ be a piecewise continuous map which is continuous on each ${D_i}$.

Definition 1

[35] A connected subset $S$ of ${D_i}$ is said to be a separation of $D_i^1$ and $D_i^2$, if for any connected subset $l \subset {D_i}$ with $l \cap D_i^1 \ne \emptyset$ and $l \cap D_i^2 \ne \emptyset$, we have $l \cap S \ne \emptyset$.

Definition 2

[35] We say that $f:{D_i} \mapsto {D_j}$ is codimension-one crossing with respect to two pairs $(D_i^1,D_i^2)$ and $(D_j^1,D_j^2)$, if $f(S) \cap {D_j}$ is also a separation of $(D_j^1,D_j^2)$ for each separation $S$ of $(D_j^1,D_j^2)$.

Theorem 1

[34, 35] If the codimension-one crossing relation $f:{D_i} \mapsto {D_j}$, holds for $1 \le i,j \le m$, then there exists a compact invariant set $K \subset D$, such that $f|K$ is semiconjugate to the m-shift. Here, the $m$-shift is usually denoted by $\sigma |\sum p$, which is also called the Bernoulli m-shift. The symbolic series space $\sum p$ is compact, totally disconnected and perfect. A set having these three properties is often defined as a Cantor set, and such a Cantor set frequently appears in the characterization of complex structures of chaotic invariant sets.

Theorem 2

[40] Let $X$ be a compact metric space and $f:X \rightarrow X$ be a continuous map. If there exists an invariant set $K \subset X$ such that $f|K$ is semiconjugate to the m-shift $\sigma |p$, then the entropy of $f$,

$$\begin{aligned} ent(f) \ge ent(\sigma ) = \mathrm{{log(p)}} \end{aligned}$$

In addition, for every positive integer $k$,

$$\begin{aligned} ent({f^2}) = k \cdot ent(\sigma ) = \mathrm{{log(p)}} \end{aligned}$$

When $p > 1$, the shift map $s$ has a positive topological entropy and, therefore, is sensitive to initial conditions, i.e., chaotic. Then, it follows that $f$ must be chaotic, too.

Sometimes in verifying existence of chaos, the Proposition 1 in this theorem is not easy to be satisfied in practice. So we have the following corollary:

Corollary 1

[35] Suppose that the map $f:D \rightarrow X$ satisfies the following assumptions:

• 1. There exists two mutually disjoint compact subsets ${D_1}$ and ${D_2}$ of $D$, and ${f^\alpha }|{D_1}$ and ${f^\beta }|{D_1}$ are homeomorphisms, where $\alpha$ and $\beta$ are positive integers.

• 2. ${f^\alpha }({D_1}) \mapsto {D_1}$, ${f^\alpha }({D_1}) \mapsto {D_2}$ and ${f^\beta }({D_2}) \mapsto {D_1}$. Then, there exists a compact invariant set $K \subset D$, such that ${f^{2\alpha + \beta }}|K$ is semiconjugate to 2-shift dynamics, and ${1 \over {2\alpha +\beta }}\log 2$.

Appendix 2. The four vertices of subset ${A_{zou}}$ and ${B_{zou}}$ in terms of $(z,u)$

When $k = 7.5$, the four vertices of subset ${A_{zou}}$ are

$$\begin{aligned} \begin{array}{l} (0.4873, - 0.3150),(0.4873, - 0.3485) \\ (0.5204, - 0.3496),(0.5211, - 0.3228) \\ \end{array} \end{aligned}$$

and the four vertices of subset ${B_{zou}}$ are

$$\begin{aligned} \begin{array}{l} (0.6684, - 0.4546),(0.6598, - 0.4993) \\ (0.6742, - 0.5205),(0.6835, - 0.4669) \\ \end{array} \end{aligned}$$

When $k = 4$, the four vertices of subset ${A_{zou}}$ are

$$\begin{aligned} \begin{array}{l} ( - 0.1932,0.2497),( - 0.1842,0.2828) \\ ( - 0.1302,0.2853),( - 0.1306,0.2513) \\ \end{array} \end{aligned}$$

and the four vertices of subset ${B_{zou}}$ are

$$\begin{aligned} \begin{array}{l} ( - 0.1619,0.3751),( - 0.1619,0.3654) \\ ( - 0.1493,0.3654),( - 0.1500,0.3759) \\ \end{array} \end{aligned}$$

When $k = 2.5$, the four vertices of subset ${A_{zou}}$ are

$$\begin{aligned} \begin{array}{l} ( - 0.3396, - 0.4986),( - 0.3103, - 0.5487) \\ ( - 0.2733, - 0.5598),( - 0.3118, - 0.4853) \\ \end{array} \end{aligned}$$

and the four vertices of subset ${B_{zou}}$ are

$$\begin{aligned} \begin{array}{l} ( - 0.3172, - 0.3307),( - 0.2795, - 0.3195) \\ ( - 0.2671, - 0.3852),( - 0.2987, - 0.3974) \\ \end{array} \end{aligned}$$