Skip to main content
SpringerLink
Log in

Theoretical study on synchronization of two exciters in a nonlinear vibrating system with multiple resonant types

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

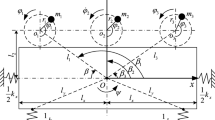
This paper aims at studying theoretically synchronization of two exciters in a nonlinear vibrating system (NVS), in which the behavior of NVS is mainly reflected at nonlinear restoring forces of springs with piecewise linear characters. The differential motion equations of two rigid frames in the horizontal direction are combined into their relative motion equation. Based on the asymptotic method, the nonlinear stiffness of springs is linearized equivalently as a function of the amplitude of the relative motion. Using Lagrange’s equations, the differential motion equations of the total system are deduced. The criterion of synchronization for two exciters in the analytical form is derived, by the average method. According to the principle that the stable solution of the synchronous states corresponds to a minimum point of Hamilton’s average action amplitude of the system, the criterion of stability of the synchronous states is achieved analytically. States of the system versus the operating frequency under consideration of multiple resonant types are presented. For the synchronous vibrating machines with two rigid frames used in engineering, the condition of the minimum of excitation to foundation is discussed, as well as the ideal working regions of the vibrating machines.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

Abbreviations

\(f_{0i}\) :

Damping coefficient of axes of the induction motor i, \(i=1,2\)

\(f_x \) :

Damping constant of the total vibrating system in x-direction

\(f_{1y}\) :

Damping constant of the relative motion between \(m_1 \) and \(m_2 \) in y-direction with respect to the shear rubber spring \(k_{1y} \)

\(\Delta f_{1y}\) :

Damping constant of the relative motion between \(m_1 \) and \(m_2 \) in y-direction with respect to the gap-activated compression rubber spring \(\Delta k_{1y} \)

\({f}'_{1y} \) :

Equivalent damping constant of the relative motion between \(m_1 \) and \(m_2 \) in y-direction

\(f_{2y}\) :

Damping constant of the isolative rigid frame \(m_2 \) in y-direction

\(f_\psi \) :

Damping constant of the total vibrating system in \(\psi \)-direction, \(f_\psi =(f_x l_y ^{2}+f_{2y} l_x ^{2})/2\)

J :

Moment of inertia of the total vibrating system about its mass center, \(J=Ml_\mathrm{e}^2 \)

\(J_{0i}\) :

Moment of inertia of the exciter i, \(J_{0i} =m_{0i} r^{2}=J_0 \), \(i=1,\;2\)

\(k_x\) :

Stiffness of the total vibrating system in x-direction

\(k_{1y}\) :

Stiffness of the shear rubber spring between \(m_1 \) and \(m_2 \) in y-direction

\(\Delta k_{1y} \) :

Stiffness of the gap-activated compression rubber spring between \(m_1 \) and \(m_2 \) in y-direction

\({k}'_{1y}\) :

Equivalent stiffness of the relative motion between \(m_1 \) and \(m_2 \) in y-direction

\(k_{2y}\) :

Stiffness of the isolative rigid frame \(m_2 \) in y- direction

\(k_\psi \) :

Stiffness of the total vibrating system in \(\psi \)-direction, \(k_\psi =(k_{2y} l_x ^{2}+k_x l_y ^{2})/2\)

\(l_\mathrm{e}\) :

Equivalent rotational radius of the total vibrating system about its mass center, \(J=Ml_\mathrm{e}^2 \)

\(l_0\) :

Distance between the rotary center of each exciter and the mass center of the isolative rigid frame \(m_2 \)

e :

Average gap between the gap-activated compression rubber spring \(\Delta k_{1y} \) and the rigid frame \(m_1 \)

m :

Induced mass of the system, \(m={M}'_1 {M}'_2 /({M}'_1 +{M}'_2)\)

\(m_0\) :

Mass of the standard exciter, \(m_{01} =m_{02} =m_0 \)

\(m_{0i}\) :

Mass of the exciter \(i,\ i=1,2\)

\(m_1\) :

Mass of the rigid frame \(m_1\)

\(m_2\) :

Mass of the isolative rigid frame \(m_2 \)

M :

Mass of the total vibrating system, \(M=m_1 +m_2 +m_{01} +m_{02}\), \(M_1,M_2 \quad M_1 =m_1 , \quad M_2 =m_2 +m_{01} +m_{02}\), \({M}'_1 ,{M}'_2 \quad {M}'_1 =M_1 ,\;{M}'_2 \approx M_2\)

r :

Eccentric radius of each exciter (it is here assumed that eccentric radiuses of two exciter are identical)

\(r_l\) :

\(r_l =l_0 /l_\mathrm{e}\)

\(r_{\mathrm {m}}\) :

Mass ratio of the standard exciter to the total vibrating system, \(r_{\mathrm {m}} =m_0 /M\)

\(r_{\mathrm {m2}}\) :

Mass ratio of the standard exciter to \(M_2 \), \(r_{\mathrm {m}2} =m_0 /M_2 \)

\(T_{\mathrm {e0}i}\) :

Electromagnetic torque of an induction motor operating steadily at the angular velocity \(\omega _{\mathrm {m0}} \), \(i=1,2\)

\(T_\mathrm{ei}\) :

Electromagnetic torque of the induction motor i, \(i=1,2\)

\(T_\mathrm{u}\) :

Energy of the standard exciter, \(T_\mathrm{u} =m_0 r^{2}\omega _{\mathrm {m0}}^{2} /2\)

\(\alpha \) :

Half of the phase difference between two exciters, \(\varphi _{01} -\varphi _{02} =2\alpha \)

\(\pi -\gamma _j\) :

Phase angle of the total vibrating system in j-direction, \(\gamma _j =\arctan \frac{2\xi _j (\omega _{\mathrm {n}j} /\omega _{\mathrm {m}0} )}{1-(\omega _{\mathrm {n}j} /\omega _{\mathrm {m}0} )^{2}}, \quad j=x,\psi \)

\(\gamma _{1y} ,\gamma _{2y}\) :

Phase angles of the rigid frames \(m_1 \) and \(m_2 \) in y-direction, respectively

\(\xi _i\) :

Critical damping ratio of the total vibrating system in i-direction, \(i=x,\psi \)

\({\xi }'_{1y}\) :

Equivalent critical damping ratio of the relative motion between \(m_1 \) and \(m_2 \) in y-direction

\(\xi _{2y}\) :

Critical damping ratio of the isolative rigid frame \(m_2 \) in y-direction

\(\varphi \) :

Average phase of two exciters

\(\varphi _{0i}\) :

Phase of exciter i, \(i=1,2\)

\(\omega _{\mathrm {m0}}\) :

Synchronous angular velocity of two exciters when the vibrating system operates in the steady state

\(\omega _{\mathrm {n}x}\) :

Natural frequency of the total vibrating system in x-direction, \(\omega _{\mathrm {n}x} =\sqrt{k_x /M}\)

\(\omega _{\mathrm {n}\psi }\) :

Natural frequency of the total vibrating system in \(\psi \)-direction, \(\omega _{\mathrm {n}\psi } =\sqrt{k_\psi /J}\)

\(\omega _0 \) :

Natural frequency of the relative motion with the inverse phases in y-direction for two rigid frames, \(\omega _0 =\sqrt{{k}'_{1y} /m}\) in the case of neglecting \(k_{2y} \)

\({\omega }'_{\mathrm {Inv}}\) :

Natural frequency of the relative motion with the inverse phases in y-direction for two rigid frames, in the case of not neglecting \(k_{2y} \)

\({\omega }'_{\mathrm {Sa}} \) :

Natural frequency of the relative motion with the same phases in y-direction for two rigid frames

\({\omega }'_1 \) :

Natural frequency of the rigid frame \(m_1 \) in y-direction, \({\omega }'_1 =\sqrt{{k}'_{1y} /M_1}\)

\(\omega _\mathrm{g}\) :

Natural frequency of the isolated system, \(\omega _\mathrm{g} =\sqrt{k_{2y} /M}\)

\(\sigma _{12}\) :

\(\sigma _{12} =\sqrt{{k}'_{1y} /M_2 }\)

\((\dot{{\bullet }})\) :

\(\hbox {d}{\bullet }/\hbox {d}t\)

\((\ddot{{\bullet }})\) :

\(\hbox {d}^{2}{\bullet }/\hbox {d}t^{2}\).

References

  1. Banerjee, T., Biswas, D., Sarkar, B.C.: Anticipatory, complete and lag synchronization of chaos and hyperchaos in a nonlinear delay-coupled time-delayed system. Nonlinear Dyn. 72, 321–332 (2013)

    Article  MathSciNet  Google Scholar 

  2. Orange, S., Verdière, N.: Nonlinear synchronization on connected undirected networks. Nonlinear Dyn. 76, 47–55 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  3. Lu, Q.S., Gu, H.G., Yang, Z.Q., et al.: Dynamics of firing patterns, synchronization and resonances in neuronal electrical activities: experiments and analysis. Acta. Mech. Sin. 24, 593–628 (2008)

    Article  MATH  Google Scholar 

  4. Yamapi, R., Woafo, P.: Dynamics and synchronization of coupled self-sustained electromechanical devices. J. Sound Vib. 285, 1151–1170 (2005)

    Article  Google Scholar 

  5. Acebrón, J.A., Bonilla, L.L., Perez Vicente, C.J., et al.: The Kuramoto model: a simple paradigm for synchronization phenomena. Rev. Mod. Phys. 77, 137–185 (2005)

    Article  Google Scholar 

  6. Acebrón, J.A., Bonilla, L.L., Spigler, R.: Synchronization in populations of globally coupled oscillators with inertial effects. Phys. Rev. E 62, 3437–3454 (2000)

    Article  MathSciNet  Google Scholar 

  7. Nayfeh, A.H., Mook, D.T.: Nonlinear Oscillations. Wiley, New York (1979)

    MATH  Google Scholar 

  8. Nayfeh, A.H.: Problems in Perturbation. Wiley, New York (1985)

    MATH  Google Scholar 

  9. Nayfeh, A.H.: Introduction to Perturbation Techniques. Wiley, New York (1981)

    MATH  Google Scholar 

  10. Blekhman, I.I.: Synchronization in Science and Technology. ASME Press, New York (1988)

    Google Scholar 

  11. Blekhman, I.I.: Synchronization of Dynamical Systems. Nauka, Moscow (1971). (in Russian)

    MATH  Google Scholar 

  12. Blekhman, I.I., Yaroshevich, N.P.: Extension of the domain of applicability of the integral stability criterion (extremum property) in synchronization problems. J. Appl. Math. Mech. 68, 839–846 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  13. Inoue, J., Araki, Y.: Self-synchronization of mechanical system (multiple cycle). Proc. Jpn. Mech. Eng. Soc. 42, 103–110 (1981). (in Japanese)

    Google Scholar 

  14. Wen, B.C., Zhang, H., Liu, S.Y., et al.: Theory and Techniques of Vibrating Machinery and their Applications. Science Press, Beijing (2010)

    Google Scholar 

  15. Wen, B.C., Fan, J., Zhao, C.Y., et al.: Vibratory Synchronization and Controlled Synchronization in Engineering. Science Press, Beijing (2009)

    Google Scholar 

  16. Wen, B.C., Li, Y.N., Zhang, Y.M., et al.: Vibration Utilization Engineering. Science Press, Beijing (2005). (in Chinese)

    Google Scholar 

  17. Balthazar, J.M., Felix, J.L.Palacios, Brasil, F.R.M.L.R.: Short comments on self-synchronization of two non-ideal sources supported by a flexible portal frame structure. J. Vib. Control 10, 1739–1748 (2004)

    Article  MATH  Google Scholar 

  18. Balthazar, J.M., Palacios, J.L., Reyolando, M.B.: Some comments on the numerical simulation of self-synchronization of four non-ideal exciters. Appl. Math. Comput. 164, 615–625 (2005)

    MathSciNet  MATH  Google Scholar 

  19. Zhang, X.L., Zhao, C.Y., Wen, B.C.: Theoretical and experimental study on synchronization of the two homodromy exciters in a non-resonant vibrating system. Shock Vib. 20, 327–340 (2013)

    Article  Google Scholar 

  20. Zhang, X.L., Wen, B.C., Zhao, C.Y.: Synchronization of three non-identical coupled exciters with the same rotating directions in a far-resonant vibrating system. J. Sound Vib. 332, 2300–2317 (2013)

    Article  Google Scholar 

  21. Zhao, C.Y., Wen, B.C., Zhang, X.L.: Synchronization of the four identical unbalanced rotors in a vibrating system of plane motion. Sci. China Technol. Sci. 53, 405–422 (2010)

    Article  MATH  Google Scholar 

  22. Zhang, X.L., Wen, B.C., Zhao, C.Y.: Vibratory synchronization and coupling dynamic characteristics of multiple unbalanced rotors on a mass-spring rigid base. Int. J. Non-Linear Mech. 60, 1–8 (2014)

    Article  Google Scholar 

  23. Natsiavas, S.: On the dynamics of oscillators with bi-linear damping and stiffness. Int. J. Non-Linear Mech. 25, 535–554 (1990)

    Article  MATH  Google Scholar 

  24. Natsiavas, S., Babcock, C.D.: Behavior of unanchored fluid-filled tanks subjected to ground excitation. J. Appl. Mech. Trans. ASME 55, 654–659 (1988)

    Article  Google Scholar 

  25. Yamapi, R., Chabi Orou, J.B., Woafo, P.: Effects of discontinuity of elasticity and damping on the dynamics of an electromechanical transducer. J. Vib. Acoust. 127, 588–593 (2005)

    Article  MATH  Google Scholar 

  26. Guzman, A.: Derivatives and Integrals of Multivariable Functions. Springer, New York (2003)

  27. Zhang, X.L., Kong, X.X., Wen, B.C., Zhao, C.Y.: Numerical and experimental study on synchronization of two exciters in a nonlinear vibrating system with multiple resonant types. Nonlinear Dyn. 82, 987–999 (2015)

    Article  MathSciNet  Google Scholar 

  28. Ni, Z.H.: Vibration Mechanics. Xi’an Jiaotong University Press, Xi’an (1989); (in Chinese)

Download references

Acknowledgments

This project is supported by National Basic Research Program of China (973 Program, Grant No. 2011CB706504) and National Natural Science Foundations of China (Grant No. 51375080).

Author information

Authors and Affiliations

  1. School of Mechanical Engineering and Automation, Northeastern University, Shenyang, 110004, China

    Xueliang Zhang, Bangchun Wen & Chunyu Zhao

Authors
  1. Xueliang Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Bangchun Wen
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Chunyu Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xueliang Zhang.

Appendix

Appendix

To solve the analytical expressions of responses for the case of the nonideal system with the coupling elements and multiple rigid frames, TFM is employed to derive it, where detailed ideas are as follows:

Fig. 2
figure 2

Flow chart of solving responses for the case of the nonideal system base on TFM

Full size image

(1) According to the definition of the Laplace transform (LT) [28], LT of x(t) is here denoted by \(L[x(t)]=X(s)\), then we have

$$\begin{aligned}&L[\dot{x}(t)]=sX(\omega _{\mathrm {m}0} )-x(0) \nonumber \\&L[\ddot{x}(t)]=s^{2}X(\omega _{\mathrm {m}0} )-sx(0)-\dot{x}(0), \end{aligned}$$
(42)

where x(0) denotes the initial displacement of the system; \(\dot{x}(0)\) the initial velocity of the system.

In this paper, since we focus on investigating responses of the system in the steady state, responses of the system excited by the free vibration for initial conditions, therefore, can be ignored. Thus, Eq. (42) can be simplified as

$$\begin{aligned}&L[\dot{x}(t)]=sX(\omega _{\mathrm {m}0} ) \nonumber \\&L[\ddot{x}(t)]=s^{2}X(\omega _{\mathrm {m}0}) \end{aligned}$$
(43)

(2) Laplace transform is applied to the differential equations of motion of the system [i.e., the first four formulae in Eq. (20)], which can convert the problem of solving the differential equations into that of solving the algebraic equations. So the transfer functions of the system (TFS), denoted by G(s), are derived.

(3) Letting \(s=i\omega _{\mathrm {m}0} \) (i is the imaginary unit), which is substituted in TFS, leads to TFS of the complex frequency domain (CFD), denoted by \(G(\omega _{\mathrm {m}0} )\).

(4) Transfer functions of CFD are multiplied by excitations of CFD (\(F(\omega _{\mathrm {m}0} ))\), and then the responses of the system of CFD in the steady state, denoted by \(X(\omega _{\mathrm {m}0})\), are obtained, which can be further converted into the final responses of the system according to their detailed types (i.e., real or imaginary component) of the external excitations.

The above detailed idea can be also illustrated by Fig. 2, and here no dwell on.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, X., Wen, B. & Zhao, C. Theoretical study on synchronization of two exciters in a nonlinear vibrating system with multiple resonant types. Nonlinear Dyn 85, 141–154 (2016). https://doi.org/10.1007/s11071-016-2674-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-016-2674-8

Keywords

Search

Navigation