Skip to main content
SpringerLink
Log in

On the nonlinear oscillations of a horizontally supported Jeffcott rotor with a nonlinear restoring force

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

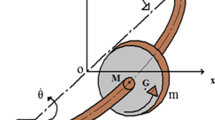
This paper deals with the vibration analysis of a horizontally supported Jeffcott rotor system. Both nonlinear restoring force and the rotor weight are considered in the system modeling. The model shows a small difference between the natural frequencies of the vertical and horizontal mode. The multiple scales perturbation technique is utilized to obtain a second-order approximate solution at the simultaneous resonance case. The bifurcation analyses are conducted. The stability of the obtained solution is investigated by applying Lyapunov first method. The influences of all the parameters on the system behavior are explored. The Effect of both the negative and positive values of the nonlinear stiffness coefficient is studied. At the large rotor eccentricity, the analysis revealed the following: (1) the existence of three different stable solutions in an interval of the rotational speed. (2) The disk exposed to two consecutive jumps if its speed crossed the resonant speed. (3) For a soft spring, localized and nonlocalized oscillation in both the horizontal and vertical mode occurs. (4) For a hard spring, nonlocalized oscillation occurs in the two directions in addition to the localized motion in the vertical direction only (5) The system is very sensitive to initial conditions. Then, numerical simulations are performed to confirm the accuracy of the approximate results. It is found that the predictions from the analytical solutions are in a good agreement with the numerical simulations. Finally, a comparison with previously published work is included.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24

Similar content being viewed by others

Abbreviations

\(u,\dot{u},\ddot{u}\) :

Displacement, velocity and acceleration of the horizontal oscillation mode, respectively

\(v,\dot{v},\ddot{v}\) :

Displacement, velocity and acceleration of the vertical oscillation mode, respectively

\(\mu _1 , \mu _2 \) :

Linear damping coefficients of both the horizontal and the vertical oscillation modes, respectively

\(\omega _1 , \omega _2 \) :

Linear natural frequencies of both the horizontal and the vertical oscillation modes, respectively

\(\lambda \) :

Cubic and quadratic nonlinearity stiffness coefficients of the rotor system

\(\varOmega \) :

The rotor system angular speed

f :

The rotor eccentricity

References

  1. Yamamoto, T.: On the vibrations of a shaft supported by bearings having radial clearances. Trans. Jpn. Soc. Mech. Eng. 21(103), 186–192 (1955)

    Article  Google Scholar 

  2. Yamamoto, T.: On the critical speed of a shaft of subharmonic oscillation. Trans. Jpn. Soc. Mech. Eng. 21(111), 853–858 (1955)

    Article  Google Scholar 

  3. Ehrich, F.F.: Subharmonic vibration of rotors in bearing clearance. ASME Paper No. 66-MD-1

  4. Ehrich, F.F.: High-order subharmonic response of highspeed rotors in bearing clearance. ASME J. Vib. Acoust. Stress. Reliab. Des. 110(1), 9–16 (1988)

    Article  Google Scholar 

  5. Yamamoto, T., Ishida, Y.: Theoretical discussions on vibrations of a rotating shaft with nonlinear spring characteristics. Trans. Jpn. Soc. Mech. Eng. Ser. C 41, 1374–1384 (1975). (in Japanese)

    Article  Google Scholar 

  6. Ganesan, R.: Dynamic response and stability of a rotor support system with non-symmetric bearing clearances. Mech. Mach. Theory 31(6), 781–798 (1996)

    Article  Google Scholar 

  7. Kim, Y., Noah, S.: Quasi-periodic response and stability analysis for a non-linear Jeffcott rotor. J. Sound Vib. 190(2), 239–253 (1996)

    Article  Google Scholar 

  8. Kim, Y., Choi, S.: A multiple harmonic balance method for the internal resonant vibration of a non-linear Jeffcott rotor. J. Sound Vib. 208(5), 745–761 (1997)

    Article  Google Scholar 

  9. Jiang, J., Ulbrich, H.: Stability analysis of sliding whirl in a nonlinear Jeffcott Rotor with cross-coupling stiffness coefficients. Nonlinear Dyn. 24, 269–283 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  10. Karpenko, E., Pavlovskaia, E., Wiercigroch, M.: Bifurcation analysis of a preloaded Jeffcott rotor. Chaos, Solitons Fractals 15, 407–416 (2003)

    Article  MATH  Google Scholar 

  11. Pavlovskaia, E., Karpenko, E., Wiercigroch, M.: Nonlinear dynamic interactions of a Jeffcott rotor with preloaded snubber ring. J. Sound Vib. 276, 361–379 (2004)

    Article  Google Scholar 

  12. Karpenko, E., Wiercigroch, M., Pavlovskaia, E., Neilson, R.: Experimental verification of Jeffcott rotor model with preloaded snubber ring. J. Sound Vib. 298, 907–917 (2006)

    Article  Google Scholar 

  13. Cveticanin, L.: Free vibration of a Jeffcott rotor with pure cubic non-linear elastic property of the shaft. Mech. Mach. Theory 40, 1330–1344 (2005)

    Article  MATH  Google Scholar 

  14. Ishida, Y., Inoue, T.: Vibration suppression of nonlinear rotor systems using a dynamic damper. J. Vib. Control 13(8), 1127–1143 (2007)

  15. Yabuno, H., Kunitho, Y., Inoue, T., Ishida, Y.: Nonlinear analysis of rotor dynamics by using the method of multiple scales. IUTAM Symposium on Dynamics and Control of Nonlinear Systems with Uncertainty, pp. 167–176. Springer (2007)

  16. Kahimura, T., Yabuno, H., Inoue, T., Ishida, Y.: Analysis of 1/2-order subharmonic resonance in a horizontally supported Jeffcott rotor. ISCV14, Cairns, Australia, 9–12 July (2007)

  17. Yabuno, H., Kashimura, T., Inoue, T., Ishida, Y.: Nonlinear normal modes and primary resonance of horizontally supported Jeffcott rotor. Nonlinear Dyn. 66, 377–387 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  18. Chavez, J., Wiercigroch, M.: Bifurcation analysis of periodic orbits of a non-smooth Jeffcott rotor model. Commun. Nonlinear Sci. Numer. Simul. 18, 2571–2580 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  19. Nayfeh, A., Mook, D.: Nonlinear Oscillations. Wiley, New York (1995)

    Book  MATH  Google Scholar 

  20. Nayfeh, A.: Perturbation Methods. Wiley, New York (1973)

    MATH  Google Scholar 

  21. Nayfeh, A.: Resolving controversies in the application of the method of multiple scales and the generalized method of averaging. Nonlinear Dyn. 40, 61–102 (2005)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Physics and Engineering Mathematics, Faculty of Electronic Engineering, Menoufia University, Menouf, 32952, Egypt

    N. A. Saeed & H. A. El-Gohary

Authors
  1. N. A. Saeed
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. H. A. El-Gohary
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to N. A. Saeed.

Appendices

Appendix 1

$$\begin{aligned} R_{11}= & {} \left[ -\frac{1}{2}\mu _1 -\frac{1}{2\omega _1 }\left( \frac{4\lambda ^{2}}{\omega _2 (\omega _2 -2\omega _1 )}\right. \right. \\&\left. \left. +\,\frac{ 2\lambda ^{2}}{\omega _2^2 }+\lambda \right) \sin (4\varphi _{10} -4\varphi _{20} )a_{20}^2 \right] \\ R_{12}= & {} \left[ \left( {1-\frac{\sigma _1 }{2\omega _1 }} \right) \frac{f\varOmega ^{2}}{2\omega _1 }\cos (2\varphi _{10} )\right. \\&-\,\frac{2}{\omega _1 }\left( \frac{4\lambda ^{2}}{\omega _2 (\omega _2 -2\omega _1 )}+\frac{ 2\lambda ^{2}}{\omega _2^2 }+\lambda \right) \\&\quad \left. \cos (4\varphi _{10} -4\varphi _{20} )a_{10} a_{20}^2 \right] \\ R_{13}= & {} -\left[ \frac{1}{\omega _1}\left( \frac{4\lambda ^{2}}{\omega _2 (\omega _2 -2\omega _1 )}+\frac{ 2\lambda ^{2}}{\omega _2^2}\right. \right. \nonumber \\&\left. \left. +\,\lambda \right) \sin (4\varphi _{10} -4\varphi _{20} )a_{10} a_{20} \right] \\ R_{14}= & {} \left[ \frac{2}{\omega _1 }\left( {\frac{4\lambda ^{2}}{\omega _2 (\omega _2 -2\omega _1 )}+\frac{ 2\lambda ^{2}}{\omega _2^2 }+\lambda } \right) \cos (4\varphi _{10} \right. \\&\left. -\,4\varphi _{20} )a_{10} a_{20}^2 \right] \\ R_{21}= & {} -\left[ \frac{1}{2\omega _1 }\left( {\frac{2\lambda ^{2}}{4\omega _1^2 -\omega _2^2}-\frac{4\lambda ^{2}}{\omega _2^2}+3\lambda } \right) a_{10}\right. \\&\left. +\,\left( {1-\frac{\sigma _1 }{2\omega _1 }} \right) \frac{f\varOmega ^{2}}{8\omega _1 a_{10}^2 }\cos (2\varphi _{10} ) \right] \end{aligned}$$
$$\begin{aligned} R_{22}= & {} \left[ \frac{1}{\omega _1 }\left( {\frac{4\lambda ^{2}}{\omega _2 (\omega _2 -2\omega _1 )}+\frac{ 2\lambda ^{2}}{\omega _2^2 }+\lambda } \right) \sin (4\varphi _{10} \right. \\&\left. -\,4\varphi _{20} )a_{20}^2-\left( {1-\frac{\sigma _1 }{2\omega _1 }} \right) \frac{f\varOmega ^{2}}{4\omega _1 a_{10} }\sin (2\varphi _{10} ) \right] \\ R_{23}= & {} -\left[ {\frac{1}{\omega _1 }} \right. \left( \frac{2\lambda ^{2}}{\omega _2 (2\omega _1 +\omega _2 )}+\frac{2\lambda ^{2}}{\omega _2 (\omega _2 -2\omega _1 )}\right. \\&\left. -\,\frac{6 \lambda ^{2}}{\omega _2^2 }+\lambda \right) a_{20}+\frac{1}{2\omega _1 }\left( \frac{4\lambda ^{2}}{\omega _2 (\omega _2 -2\omega _1 )}\right. \\&\left. \left. +\,\frac{ 2\lambda ^{2}}{\omega _2^2 }+\lambda \right) {\cos (4\varphi _{10} -4\varphi _{20} )a_{20} } \right] \\ R_{24}= & {} -\left[ \frac{1}{\omega _1 }\left( {\frac{4\lambda ^{2}}{\omega _2 (\omega _2 -2\omega _1 )}+\frac{2\lambda ^{2}}{\omega _2^2}+\lambda } \right) \right. \\&\left. \sin (4\varphi _{10} -4\varphi _{20})a_{20}^2 \right] \\ R_{31}= & {} -\left[ \frac{1}{\omega _2 }\left( {\frac{4\lambda ^{2}}{\omega _2 (\omega _2 -2\omega _1 )}+\frac{6\lambda ^{2}}{4\omega _1^2 -\omega _2^2 }+\lambda }\right) \right. \\&\left. \sin (4\varphi _{20} -4\varphi _{10} )a_{10} a_{20} \right] \\ R_{32}= & {} \left[ \frac{2}{\omega _2 }\left( {\frac{4\lambda ^{2}}{\omega _2 (\omega _2 -2\omega _1 )}+\frac{6\lambda ^{2}}{4\omega _1^2 -\omega _2^2 }+\lambda } \right) \right. \end{aligned}$$
$$\begin{aligned}&\left. \cos (4\varphi _{20} -4\varphi _{10} )a_{10}^2 a_{20} \right] \\ R_{33}= & {} -\left[ \frac{1}{2}\mu _2 +\frac{1}{2\omega _2 }\left( \frac{4\lambda ^{2}}{\omega _2 (\omega _2 -2\omega _1)}\right. \right. \\&\left. \left. +\,\frac{6\lambda ^{2}}{4\omega _1^2 -\omega _2^2 }+\lambda \right) \sin (4\varphi _{20} -4\varphi _{10} )a_{10}^2 \right] \\ R_{34}= & {} \left[ -\frac{2}{\omega _2 }\left( {\frac{4\lambda ^{2}}{\omega _2 (\omega _2 -2\omega _1 )}+\frac{6\lambda ^{2}}{4\omega _1^2 -\omega _2^2 }+\lambda } \right) \right. \\&\left. \times \cos (4\varphi _{20}-4\varphi _{10} )a_{10}^2 a_{20} \right. \\&\left. {-\left( {\frac{\sigma _1 -\sigma _2 }{2\omega _2 }-1} \right) \frac{f\varOmega ^{2}}{2\omega _2 }\sin (2\varphi _{20} )} \right] \\ R_{41}= & {} -\left[ \frac{1}{\omega _2 }\left( \frac{2\lambda ^{2}}{\omega _2 (2\omega _1 +\omega _2 )}\right. \right. \\&\left. \left. +\,\frac{2\lambda ^{2}}{\omega _2 (\omega _2 -2\omega _1 )}-\frac{6\lambda ^{2}}{\omega _2^2 }+\lambda \right) \right. a_{10} \\&+\,\frac{1}{2\omega _2 }\left( {\frac{4\lambda ^{2}}{\omega _2 (\omega _2 -2\omega _1 )}+\frac{6\lambda ^{2}}{4\omega _1^2 -\omega _2^2 }+\lambda } \right) \\&\left. {\cos (4\varphi _{20} -4\varphi _{10} )a_{10} } \right] \\ R_{42}= & {} -\left[ \frac{1}{\omega _2 }\left( {\frac{4\lambda ^{2}}{\omega _2 (\omega _2 -2\omega _1 )}+\frac{6\lambda ^{2}}{4\omega _1^2 -\omega _2^2 }+\lambda } \right) \right. \\&\left. \sin (4\varphi _{20} -4\varphi _{10} )a_{10}^2\right] \\ R_{43}= & {} -\left[ \frac{1}{2\omega _2 }\left( {-\frac{30 \lambda ^{2}}{\omega _2^2 }+3\lambda } \right) a_{20}\right. \\&\left. +\left( {1-\frac{\sigma _1 -\sigma _2 }{2\omega _2 }} \right) \frac{f\varOmega ^{2}}{8\omega _2 a_{20}^2 }\sin (2\varphi _{20}) \right] \\ R_{44}= & {} \left[ \frac{1}{\omega _2 }\left( {\frac{4\lambda ^{2}}{\omega _2 (\omega _2 -2\omega _1 )}+\frac{6\lambda ^{2}}{4\omega _1^2 -\omega _2^2 }+\lambda }\right) \right. \\&\sin (4\varphi _{20} -4\varphi _{10} )a_{10}^2 \\&\left. +\left( {1-\frac{\sigma _1 -\sigma _2 }{2\omega _2 }} \right) \frac{f\varOmega ^{2}}{4\omega _2 a_{20} }\cos (2\varphi _{20} ) \right] \end{aligned}$$

Appendix 2

$$\begin{aligned} \rho _1= & {} -R_{44} -R_{33} -R_{22} -R_{11}\\ \rho _2= & {} R_{11} R_{44} +R_{11} R_{33} +R_{11} R_{22} +R_{22} R_{44} \\&+\,R_{22} R_{33}+R_{33} R_{44} -R_{21} R_{12} -R_{31} R_{13} \\&-\,R_{41} R_{14} -R_{34} R_{43}-R_{32} R_{23} -R_{42} R_{24} \\ \rho _3= & {} R_{11} R_{32} R_{23} -R_{31} R_{12} R_{23} -R_{11} R_{22} R_{44} \\&-\,R_{42} R_{23} R_{34} +R_{31} R_{22} R_{13} +R_{32} R_{23} R_{44} \\&-\,R_{11} R_{22} R_{33} -R_{32} R_{43} R_{24} \\&-\,R_{21} R_{32} R_{13} +R_{11} R_{42} R_{24} +R_{31} R_{13} R_{44} \\&+\,R_{21} R_{12} R_{44} -R_{21} R_{42} R_{14} +R_{42} R_{24} R_{33} \\&+R_{21} R_{12} R_{33} -R_{11} R_{33} R_{44} \\&-\,R_{22} R_{33} R_{44} -R_{41} R_{12} R_{24} -R_{31} R_{43} R_{14} \\&+\,R_{41} R_{22} R_{14} +R_{22} R_{34} R_{44} +R_{41} R_{14} R_{33} \\&+\,R_{11} R_{34} R_{43} -R_{41} R_{13} R_{34} \\ \rho _4= & {} -R_{41} R_{12} R_{23} R_{34} -R_{21} R_{12} R_{33} R_{44} \\&+\,R_{11} R_{22} R_{33} R_{44} -R_{11} R_{42} R_{24} R_{33} \\&+R_{21} R_{32} R_{13} R_{44} +R_{11} R_{32} R_{43} R_{24} \\&-\,R_{41} R_{32} R_{13} R_{24} +R_{41} R_{32} R_{23} R_{14} \\&-\,R_{11} R_{22} R_{34} R_{43} +R_{21} R_{12} R_{34} R_{43} \\&-\,R_{31} R_{12} R_{43} R_{24} -R_{21} R_{42} R_{13} R_{34} \\&-\,R_{21} R_{32} R_{43} R_{14} +R_{31} R_{12} R_{14} R_{44} \\&+\,R_{31} R_{42} R_{13} R_{24} -R_{31} R_{42} R_{23} R_{14} \\&+\,R_{21} R_{42} R_{14} R_{33} +R_{11} R_{42} R_{23} R_{34} \\&-\,R_{11} R_{32} R_{23} R_{44} +R_{31} R_{22} R_{43} R_{14} \\&-\,R_{31} R_{22} R_{13} R_{44} +R_{41} R_{12} R_{24} R_{33} \\&-\,R_{41} R_{22} R_{14} R_{33} +R_{41} R_{22} R_{13} R_{34} \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Saeed, N.A., El-Gohary, H.A. On the nonlinear oscillations of a horizontally supported Jeffcott rotor with a nonlinear restoring force. Nonlinear Dyn 88, 293–314 (2017). https://doi.org/10.1007/s11071-016-3243-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-016-3243-x

Keywords

Search

Navigation