1 Introduction

A lot of literature exists on analyzing a d-link robot when the external torque applied to it through motors has a noise/disturbance component. Various kinds of disturbance observers have been designed to estimate the disturbance based on measurements of the angular positions and velocities of the links. After designing the disturbance observer using such real-time algorithms, we subtract it from the torque input, thereby reducing the disturbance. Apart from motor noise, disturbance can come from hand tremor or jerks if we are dealing with only a master robot or it can come from jerky environment if we are dealing only with slave robots. Modeling the disturbance as white Gaussian noise processes and estimating the parameters of the robot based on such a Gaussian statistical model have been discussed in the existing literature [1, 2].

Some work [1] also exists in proving stability theorems for robots with Gaussian noise using stochastic Lyapunov theory. This analysis is based on calculating the rate of change on the ensemble averaged Lyapunov energy function using Ito’s formula for Brownian motion. However, in many instances, it is not possible to model the disturbance as a Gaussian process. This is especially true if the robot links experience sudden jerks of random amplitudes at random times. If the successive jerks are independent and the inter-jerk time is an exponential random variable, then the accumulated effect of the jerks can be successfully modeled as a compound Poisson process or more generally as a Lévy process, i.e., a stochastic process with independent increments. Examples include Gaussian distributed, uniformly distributed and exponentially distributed jump amplitudes.

The Lévy process is Markovian and has independent increments. However, there is another property [3] which states that any Lévy process is a limit of finite superposition of independent Poisson processes and Poisson processes are pure jump processes. When a human operator handles a robot, jerk tremors will be present (especially if the hand has something like Parkinson’s disease) and these jerks are pure jumps of varying magnitude which can be modeled using Poisson processes.

Another situation involves modeling the motion of a slave robot in a rough environment which generates jerk noise acting on the slave robot.

In this paper, we study the effect of Lévy processes on a two-link robot manipulator. We simulate Lévy processes and study the solution of the robot differential equation subject to Lévy noise using simulations.

We also calculate the average Lyapunov energy for the trajectory tracking error and also the statistical fluctuations in the Lyapunov energy. These calculations are based on Ito’s formula for the Poisson process. In the case of white Gaussian noise, differentials of the tracking error amplitude have negligible third and higher moments owing to Ito’s formula, not so for general Lévy processes. Differentials of the error of degree three and higher play a role in the computation of the fluctuations in the Lyapunov energy, and we therefore get a higher value of the energy fluctuations in the Lévy case than in the Gaussian case. This effect can also be explained by noting that an accumulated sequence of finite independent random variables has a large fluctuation as compared to an accumulated sequence of small random variables owing to the applicability of the central limit theorem in the latter case.

In this paper, we also study the maximum likelihood method of parameter estimation of a two-link robot based on measurements of the total number of jerks suffered by the robot angular variables in a fixed time duration. Specifically we show how the times at which the jerks take place and the size of the angular jumps can be estimated. Our formula for the maximum likelihood estimate should be compared to the case of white Gaussian noise.

In “Appendix,” we discuss algorithms for estimating parameters in SDEs driven by Lévy processes and general theory for statistical analysis of a Lévy process-driven stochastic differential equation (SDE) including an infinite series formula for the rate of change in the average of any Lyapunov function of a process satisfying a SDE driven by a Lévy process that is representable as a sum of a Poisson number of independent random vectors.

In summary, this paper analyzes statistical properties of classical robots perturbed by Lévy noise and derives parameter estimation algorithms.

As a final application, we address the important problem of rejecting the Lévy disturbance from the system dynamics using techniques of nonlinear filtering theory, i.e., estimate the current state based on past noisy measurements, and then use this state estimate to estimate the current Levy disturbance which is subtracted from the dynamics at the next time instant.

2 Review of literature

In [4], the authors consider an SDE in \({\mathbb {R}}\) driven by a Lévy process characterized by a Brownian motion process and a Poisson field. The process considered has a special form, namely the coefficients of the Brownian motion and Poisson fields are linear functions of the state. By applying Ito’s formula for Brownian and Poisson processes, they arrive at a formula for the rate of change in a Lyapunov function of the error between the state process of the Lévy-driven SDE and a stationary solution of the same. Using this, they are able to characterize the Lyapunov of exponent of the error. Our robot model is a bit more complicated in that the coefficients of the Lévy noise are vector-valued nonlinear functions of the state process. Nevertheless, the results of [4] may be extended and applied to our model by considering a linearized approximation. We have in our paper also made a small attempt to bound the Lyapunov function by an exponentially increasing function of time, and this result may be compared to [4] in the context of Lyapunov exponents.

In [5], an ordinary delay differential equation with time-varying delays has been considered. This dynamics has been stabilized by adding a Lévy noise component with state-dependent coefficient. For this, the authors apply Ito’s formula for the Brownian and Poisson fields to compute the average Lyapunov function. They prove that under certain assumptions on the infinitesimal generator of the Lévy process applied to the Lyapunov function, its rate of increase is lower and upper bounded by certain nice functions and then using this result, they deduce asymptotic stability of the stochastic Lévy modified system. To establish this result, they make use of Markovian stop time theory like Doob’s optional sampling theorem. This theory can definitely be generalized to multivariate state variable differential systems with delay, and we can hope therefore to apply it to master and slave robots communicating via time-varying teleoperation delays. This will be the subject of a future paper by us.

In [6], stochastic exponential stability of differential equations perturbed by Lévy noise that can be represented as the sum of Brownian motion and a superposition of Poisson processes is investigated. Under local Lipschitz conditions on the coefficients of the SDE, they prove zero crossing theorems as well as Martingale convergence theorems which are interpreted as strong laws of large numbers. They then perturb the system by large jump Poisson processes and prove that the system is exponentially stable, i.e., almost sure asymptotic boundedness of \(\frac{\log |x(t)|}{t}\). We can apply the results of [6] to our problem, since [6] deals with vector-valued processes driven by vector-valued Poisson processes. In order to do so, we must verify appropriate Lipschitz conditions. Applebaum and Siakalli [6] presents a beautiful computation of the Lyapunov exponent \(\limsup \limits _{t\rightarrow \infty }\frac{\log |x(t)|}{t}\), and we need to apply it to the two-link system. Moreover in [6, 7], a special form of the coefficient matrices of the Lévy noise has been chosen to prove exponential stability. We need to generalize this for general coefficients appearing in robotics.

In [8], existence and uniqueness theory for general stochastic differential equations driven by a continuous superposition of Poisson fields with the coefficients in the superposition being causal functionals of the state vector which takes values in a separable Hilbert space has been developed. This theory can be applied to the robot problem when the dynamical equations have the form

$$\begin{aligned} \mathrm{d}q(t)= & {} q'(t)\mathrm{d}t, \end{aligned}$$
(1)
$$\begin{aligned} \mathrm{d}q'(t)= & {} -M^{-1}(q(t))N(q(t),q'(t))\nonumber \\&+\,M^{-1}(q(t))\int \limits _{u\in E}^{}F(t,u,q,q')N(\mathrm{d}t,\mathrm{d}u)\nonumber \\ \end{aligned}$$
(2)

where \(F(t,u,q,q')\) for any \(u\in E\) is a functional of \(\{q(s),q'(s),s\le t\}\), i.e., F is a causal functional of the state vector. Such a model is valid when the intensity of the jerk noise is state dependent and has memory, i.e., the intensity depends on the past orientation and angular velocities of the robot. This may happen when a feedback is used to control the motion of the robot.

In [9], the authors study linear SDE’s driven by bivariate Lévy process as generalized Ornstein–Uhlenbeck (OU) processes associated with Brownian motion. If we consider a linearized robot around a given trajectory with Lévy jerks, then the “error process” as discussed in the body of our paper satisfies a similar equation. More generally consider a SDE

$$\begin{aligned} \mathrm{d}\xi (t)=f(\xi (t))\mathrm{d}t+g(\xi (t))\mathrm{d}V_t \end{aligned}$$
(3)

let \(\mathrm{d}\xi _0(t)=f(\xi _0(t))\mathrm{d}t\) be the “equilibrium trajectory” and \(e(t)=\xi (t)-\xi _0(t)\) the error process. Then we have approximately,

$$\begin{aligned} \mathrm{d}e(t)&=f'(\xi _0(t))e(t)\mathrm{d}t\nonumber \\&\quad +g(\xi _0(t)) \mathrm{d}V_t+g'(\xi _0(t))e(t)\mathrm{d}V_t \end{aligned}$$
(4)

where \(V_t\) is Lévy process. This can be expressed in the form

$$\begin{aligned} \mathrm{d}e(t)&=\left[ f'(\xi _0(t))\mathrm{d}t+g'(\xi _0(t))\mathrm{d}V_t \right] e(t)\nonumber \\&\quad +\,g(\xi _0(t))\mathrm{d}V_t \end{aligned}$$
(5)

[9] studies a generalization of this linear SDE in which the differential process

$$\begin{aligned} f'(\xi _0(t))\mathrm{d}t + g(\xi _0(t))\mathrm{d}V_t \end{aligned}$$
(6)

is replaced by the differential \(G_tdW_t\) where \(W_t\) is a Lévy process different from \(V_t\). We can thus apply the results of [9] to our linearized robot dynamics.

In [10], the heat equation with Lévy noise is studied. Existence results are established generalization including the study of partial differential equations driven by Lévy process, i.e., field u(t, x) satisfying

$$\begin{aligned} \frac{\partial u(t,x)}{\partial t}=L_1u(t,x)+(L_2u(t,x))w(t,x) \end{aligned}$$
(7)

where \(L_1\) and \(L_2\) are partial differential operators in the variable \(x\in {\mathbb {R}}^n \) and w(t, x) is a white noise field, not necessarily Gaussian. Thus

$$\begin{aligned} \int \limits _{0}^{t}w(\tau ,x)\mathrm{d}\tau =L(t,x) \end{aligned}$$
(8)

is a Lévy noise field, i.e., its increments \(L(t_{k+1}-t_k\ldots ), k=1,2,\ldots \) are independent fields for \(t_1,t_2,\ldots \). This idea can be generalized to the situation of a distribution of robots or flexible robots whose angular configuration is specified by q(t, x). There may be an interaction potential energy between two robots at locations x, y or equivalently an energy between the configurations at x and y. The Lagrangian then has the form

$$\begin{aligned} \frac{1}{2}\int \limits _{}^{}\left( \frac{\partial q}{\partial t}(t,x)\right) ^T&M(q(t,x))\frac{\partial q}{\partial t}(t,x)\mathrm{d}^3x\nonumber \\&\quad -\int \limits _{}^{}U(q(t,x),q(t,y))\mathrm{d}^3x\mathrm{d}^3y \end{aligned}$$
(9)

the result of applying the Euler–Lagrange equation to this action functional is

$$\begin{aligned} \frac{\partial }{\partial t}\left[ M(q(t,x))\frac{\partial q}{\partial t}(t,x)\right]&=\frac{1}{2}\frac{\partial }{\partial q(t,x)} \left( \left( \frac{\partial q}{\partial t}\right) ^TM(q)\frac{\partial q}{\partial t}\right) \nonumber \\&\quad -2\int \limits _{}^{}\frac{\partial U}{\partial q(t,x)}\left( q(t,x),q(t,y)\right) \mathrm{d}^3y \end{aligned}$$
(10)

In addition if a Lévy noise field w(t, x) is present, the right-hand side of (10) acquires a random torque term of the general form

$$\begin{aligned} \int \limits _{}^{}K(q(t,x),\frac{\partial q}{\partial t}(t,x),x,y)w(t,y)\mathrm{d}^3y \end{aligned}$$
(11)

and the resulting equation can be analyzed for the statistics of fluctuations.

In [11], the authors construct the ML estimator for Gaussian signals in the presence of a random medium which varies impulsively causing the received signal field to have a Lévy distribution of the \(\alpha \)-stable type. In effect, the parameters in a signal model having the representation as a superposition of Gaussian and Poisson processes are estimated by the ML method. The model considered is the direction of arrival (DOA) model in which the source signal statistics and the DOA’s are to be estimated. We can use the results of [11] in our robot problem by considering \(\alpha \)-stable Lévy noise and constructing the ML estimator for the robot parameters, namely the link masses and lengths from measurements on the angular positions. This would be a block processing approach. We could go a step further and consider estimating the robot parameters on a real-time bases from noisy measurements of the robot angular positions or end effector positions using an extended Kalman filter (EKF) developed for \(\alpha \)-stable Lévy process white noise and measurement noise.

Asymptotic equivalence of Gaussian white noise processes [12, 13] and Lévy processes has been studied in [14]. However, in general the behavior of Lévy process over a short time duration is very different from that of Gaussian noise.

If we assume that the jerks are statistically independent of each other, then these jerks must be modeled as the differentials of a process having independent increments (i.e., non-Gaussian white noise). If we further assume that this jerk noise is a stationary stochastic process, then the process increments must be stationary and we know from the basic Kolmogorov–Levy–Khintchine theorem that any such process can be represented as the limit in probability of a sequence of compound Poisson processes. A delightful proof of this fact is contained in [15]. Thus as an approximation, it is worth modeling a jerk process as a superposition of compound Poisson processes. Some of the useful references containing these ideas are [16,17,18].

The main contributions of our paper are as follows: (a) derivation of a linearized SDE for the tracking error process and parametric estimation error process-driven by a compound Poisson process. (b) Solution to the compound Poisson process-driven SDE using a state variable approach. (c) Theoretical expressions for the average rate of increase/decrease in a quadratic Lyapunov energy function of the tracking and parametric estimation errors with simulation plots. (d) Theoretical expressions for average rate of increase/decrease in arbitrary functions of the tracking and parametric estimation errors that explicitly display the difference between Ito’s calculus for Brownian motion and Poisson processes. (e) Path integral expressions for the likelihood function for varying time delay and robot parametric uncertainties. (f) General approximate expressions for the likelihood function of parametric uncertainties and fixed time delay. (g) Verification of the Jerk theory developed using hardware Phantom Omni Bundle as well as MATLAB-based simulational studies.

3 Problem formulation

We first formulate the SDE for a robot with the perturbation to the input torque being a Lévy process modeled as a compound Poisson process, i.e., as a sum of i.i.d. random variables taken N(t) times where N(.) is a Poisson process. The input torque is the computed torque for a desired trajectory \(q_d(t)\) with proportional derivative feedback control included for tracking purpose. We also assume parametric uncertainty for the robot. By linearizing around the true parameter values, and assuming the trajectory tracking error \(e(t)=q_d(t)-q(t)\) to be small, we derive a second-order linear differential equation for the error process e(t) which contains the parametric estimation error \(\delta \theta (t)\). The model for the robot dynamics is

$$\begin{aligned}&M(q(t),\theta _0)\ddot{q}(t)+N(q(t),\dot{q}(t),\theta _0)\nonumber \\&\quad = M(q(t),\hat{\theta }(t))(\ddot{q_d}(t) +K_pe(t)+K_d\dot{e}(t))\nonumber \\&\quad \quad +N(q(t),\dot{q}(t),\hat{\theta }(t))+w(t) \end{aligned}$$
(12)

where \(\hat{\theta }(t)\) is the estimate of the robot parameters \(\theta _0\) based on observation collected up to time t.

$$\begin{aligned}&e(t)= q_d(t)-q(t), \end{aligned}$$
(13a)
$$\begin{aligned}&\dot{e}(t)=\dot{q}_d(t)-\dot{q}(t), \end{aligned}$$
(13b)
$$\begin{aligned}&w(t)=\frac{\mathrm{d}}{\mathrm{d}t}\sum _{k=1}^{N(t)}Y_k=Y_{N(t)+1}\frac{\mathrm{d}N(t)}{\mathrm{d}t} \end{aligned}$$
(13c)

where \(\{Y_k\}\) is an i.i.d. sequence in \({\mathbb {R}}^{2}\) and \(\{N(t):t\ge 0\}\) is a Poisson process.

The above model for the robot dynamics is derived from the Lagrangian

$$\begin{aligned} {\mathcal {L}}(q,\dot{q},t)=\frac{1}{2}\dot{q}^TM(q)\dot{q}-V(q)+\tau (t)^Tq \end{aligned}$$
(14)

with a damping torque \(N(q,\dot{q})\) and noise torque included in \(\tau \). The Euler–Lagrange equations [19] are given by

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial {\mathcal {L}}}{\partial \dot{q}}-\frac{\partial {\mathcal {L}}}{\partial q}=-N(q,\dot{q}) \end{aligned}$$
(15)

This results in the given differential equation, where M(q) is the mass-moment of inertia matrix and \(\frac{1}{2}\dot{q}^TM(q)\dot{q}\) is the kinetic energy of the robot. V(q) is the gravitational potential energy. \(K_p and K_d\) are, respectively, position and velocity error gain coefficients. Thus, w(t) is a special kind of Lévy noise differential. Writing \(\hat{\theta }(t)-\theta _0=\delta \theta (t)\), we get approximately, from (12) and \(\ddot{q}=\ddot{q}_d-\ddot{e}\),

$$\begin{aligned}&M(q(t),\theta _0)(\ddot{e}+K_pe+K_d\dot{e})\nonumber \\&\quad =-\left[ \frac{\partial M}{\partial \theta }(q(t),\theta _0)\otimes \ddot{q}_d\right] \delta \theta (t)\nonumber \\&\qquad -\frac{\partial N}{\partial \theta }(q(t),\dot{q}(t),\theta _0)\delta \theta (t)-w(t) \end{aligned}$$
(16a)

or equivalently,

$$\begin{aligned} \ddot{e}+K_pe+K_d\dot{e}= & {} W(t,q(t),\dot{q}(t))\delta \theta (t)\nonumber \\&-\,M(q(t), \theta _0)^{-1}w(t) \end{aligned}$$
(16b)

where

$$\begin{aligned} W(t,q,\dot{q})&=-M(q,\theta _0)^{-1}\nonumber \\&\quad \left[ \frac{\partial M}{\partial \theta }(q,\theta _0)\otimes \ddot{q}_d(t)+\frac{\partial N}{\partial \theta }(q,\dot{q},\theta _0)\right] \end{aligned}$$
(17)

An explicit computation for W is given in [1]. Further, we assume a parameter update equation

$$\begin{aligned} \delta \dot{\theta }(t)=F(t)\tilde{e}(t)+H(t)\delta \theta (t)+v(t) \end{aligned}$$
(18)

where \(\tilde{e}=\left[ \begin{array}{c} e\\ \dot{e} \end{array}\right] \) and v(t) is another Lévy noise differential

$$\begin{aligned} v(t)=Z_{\tilde{N}(t)+1}\frac{\mathrm{d}\tilde{N}(t)}{\mathrm{d}t} \end{aligned}$$
(19)

with \(\{Z_k\}\) iid in \({\mathbb {R}}^4\) and \(\tilde{N}(.)\) a Poisson process independent of N(.).

3.1 Lyapunov energy function

As in the existing literature [1] we define a quadratic Lyapunov function of e(t) and \(\delta \theta (t)\) which decreases monotonically to zero as \(t\rightarrow \infty \) in the noiseless case provided that we assume an appropriate parametric update equation. Like the robot dynamics, we also assume that the parametric update equation also contains a Lévy noise component and then obtain a expression for the average rate of change in the Lyapunov function using Ito’s formula for Poisson process. In passing, in order to illustrate the difference between the effects of white Gaussian noise and compound Poisson noise on a robot, we give a sample computation of the average rate of change in an arbitrary function of e(t) and \(\delta \theta (t)\). Unlike the white Gaussian noise case where this average rate of change involves only up to two partial derivative of the Lyapunov function, in the compound Poisson case, all partial derivatives come into the picture. Consider now a Lyapunov energy function

$$\begin{aligned} V(t)=\frac{1}{2}\tilde{e}^T(t)Q_1\tilde{e}(t)+\frac{1}{2} \delta \theta (t)^TQ_2\delta \theta (t) \end{aligned}$$
(20)

Equation (16b) can be approximately expressed as

$$\begin{aligned} \mathrm{d}\tilde{e}(t)&=\left[ \begin{array}{cc} 0 &{} I_2\\ -K_pI_2 &{} -K_dI_2 \end{array}\right] \tilde{e}(t)\mathrm{d}t+\tilde{W}(t)\delta \theta (t)\mathrm{d}t\nonumber \\&\quad -G(t)Y_{N(t)+1}dN(t) \end{aligned}$$
(21)

where \(\tilde{W}(t)=\left[ \begin{array}{c} 0\\ W(t,q_d,\dot{q_d}) \end{array}\right] \), \(G(t)=\left[ \begin{array}{c} 0\\ M^{-1}(q_d(t)) \end{array}\right] \).

This approximation involves neglecting terms of order \((q_d-q)\otimes \delta \theta \) and higher.

Remark 1

If this linearized approximation is not made, then we would get an equation of the form

$$\begin{aligned} \mathrm{d}\tilde{e}(t)&=(A\tilde{e}(t)+G_1(t,\tilde{e}(t))\delta \theta (t))\mathrm{d}t\nonumber \\&\quad +\delta .G_2(t,\tilde{e}(t))Y_{N(t)+1}\mathrm{d}N(t) \end{aligned}$$
(22)

i.e., the coefficients of the Lévy-driven SDE would depend on the state \(\tilde{e}(t)\).

To solve this, we would have to write

$$\begin{aligned} G_1(t,\tilde{e}(t))= & {} W_0(t)+\sum \limits _{k\ge 1}^{}\delta ^kW_{1k}(t)(I\otimes \tilde{e}(t)^{\otimes k}) \end{aligned}$$
(23a)
$$\begin{aligned} G_2(t,\tilde{e}(t))= & {} G_{2,0}(t)+\sum \limits _{k\ge 1}^{}\delta G_{2k}(t)\tilde{e}^{\otimes k}(t) \end{aligned}$$
(23b)

where \(\delta \) is a small perturbation parameter. We can then expand the solution

$$\begin{aligned} \tilde{e}(t)=\sum \limits _{k=0}^{\infty }\delta ^k\tilde{e}_k(t) \end{aligned}$$
(24)

substituting this expression into the SDE and equating equal powers of \(\delta \), gives

$$\begin{aligned} \mathrm{d}\tilde{e}_0(t)= & {} (A\tilde{e}_0(t)+W_0(t)\delta \theta (t))\mathrm{d}t \end{aligned}$$
(25)
$$\begin{aligned} \mathrm{d}\tilde{e}_k(t)= & {} [(A+W_0(t)(\delta \theta \otimes I))\tilde{e}_k(t)\nonumber \\&+\sum _{m+r_1+2r_2+\cdots +mr_m=k,m\ge 1,r_1,r_2,\ldots ,r_m\ge 0} W_{1m}(t)\nonumber \\&\times \,(I\otimes \tilde{e}_0(t)^{\otimes r_0}\otimes \tilde{e}_1(t)^{\otimes r_1}\otimes \ldots \otimes \tilde{e}_m(t)^{\otimes r_m})]\mathrm{d}t\nonumber \\&+\sum _{m\ge 0,1+r_1+2r_2+\cdots +mr_m=k,r_0,r_1,\ldots ,r_m\ge 0} G_{2m}(t)\nonumber \\&\times \,\tilde{e}_0(t)^{\otimes r_0}\otimes \tilde{e}_1(t)^{\otimes r_1}\otimes \ldots \otimes \tilde{e}_m(t)^{\otimes r_m}\nonumber \\&\quad Y_{N(t)+1}\mathrm{d}N(t) \end{aligned}$$
(26)

This gives us an iterative stochastic integral algorithm for calculating the processes \(\tilde{e}_k(t)\). The expressions will be in term of multiple stochastic integrals with respect to the processes

$$\begin{aligned} \sum \limits _{k=1}^{N(t)}Y_k=\int \limits _{0}^{t}Y_{N(s)+1}\mathrm{d}N(s) \end{aligned}$$
(27)

The successive approximation \(e_k(t)\) will have mean varying as the kth moment of the \(Y_k's\) and variance as the 2kth moment of the \(Y_k's\). Hence, our linearized approximation (21) will be good enough if the \(Y_k's\) have small variances as compared to the initial error energy \(||\tilde{e}(0)||^2\).

Likewise Eq. (18) can be expressed as

$$\begin{aligned} \mathrm{d}\delta \theta (t)=(F(t)\tilde{e}(t)+H(t)\delta \theta (t))\mathrm{d}t+Z_{\tilde{N}(t)+1}\mathrm{d}\tilde{N}(t) \end{aligned}$$
(28)

Let \(A=\left[ \begin{array}{cc} 0 &{} I_2\\ -K_pI_2 &{} -K_dI_2 \end{array}\right] \). Then, Ito’s formula gives

$$\begin{aligned} \mathrm{d}V(t)&=\tilde{e}^TQ_1\mathrm{d}\tilde{e}+\frac{1}{2}\mathrm{d}\tilde{e}^TQ_1\mathrm{d}\tilde{e}\nonumber \\&\quad +\delta \theta ^TQ_2\mathrm{d}\delta \theta + \frac{1}{2}\mathrm{d}\delta \theta ^TQ_2\mathrm{d}\delta \theta \nonumber \\&=\frac{1}{2}\tilde{e}^T\left( Q_1A+A^TQ_1\right) \tilde{e}\mathrm{d}t+\tilde{e}^TQ_1\tilde{W}\delta \theta \mathrm{d}t\nonumber \\&\quad -\tilde{e}^TQ_1GY_{N(t)+1}\mathrm{d}N(t)\nonumber \\&\quad +\frac{1}{2}Tr\left\{ G^TQ_1GY_{N(t)+1}Y_{N(t)+1}^T\mathrm{d}N(t)\right\} \nonumber \\&\quad +\delta \theta ^TQ_2(F\tilde{e}+H\delta \theta )\mathrm{d}t\nonumber \\&\quad +\frac{1}{2}Tr\left\{ Q_2Z_{\tilde{N}(t)+1}Z^T_{\tilde{N}(t)+1}\mathrm{d}\tilde{N}(t)\right\} \nonumber \\&\quad +\delta \theta ^TQ_2Z_{\tilde{N}(t)+1}\mathrm{d}\tilde{N}(t) \end{aligned}$$
(29)

We assume that

$$\begin{aligned} Q_1\tilde{W}+F^TQ_2=0 \end{aligned}$$
(30)

i.e., \(F=Q_2^{-1}\tilde{W}^TQ_1\). Then,

$$\begin{aligned} \mathrm{d}V(t)&=\frac{1}{2}\tilde{e}^T\left( Q_1A+A^TQ_1\right) \tilde{e}\mathrm{d}t -\tilde{e}^TQ_1GY_{N(t)+1}\mathrm{d}N(t)\nonumber \\&\quad +\frac{1}{2}Tr\left\{ G^TQ_1GY_{N(t)+1}Y^T_{N(t)+1}\right\} \mathrm{d}N(t)\nonumber \\&\quad +\frac{1}{2}\delta \theta ^T\left( Q_2H+H^TQ_2\right) \delta \theta \mathrm{d}t\nonumber \\&\quad +\frac{1}{2}Tr\left( Q_2Z_{\tilde{N}(t)+1}Z^T_{\tilde{N}(t)+1}\right) \mathrm{d}\tilde{N}(t)\nonumber \\&\quad +\delta \theta ^TQ_2Z_{\tilde{N}(t)+1}\mathrm{d}\tilde{N}(t) \end{aligned}$$
(31)

Assuming that \({\mathbb {E}} Y_k=0\), \({\mathbb {E}} Z_k=0\), \({\mathbb {E}} \mathrm{d}N(t)=\lambda \mathrm{d}t\) and \({\mathbb {E}} \mathrm{d}\tilde{N}(t)=\tilde{\lambda }\mathrm{d}t\), we get with \(R_{{\tilde{e}}{\tilde{e}}}(t)={\mathbb {E}}({\tilde{e}}(t){\tilde{e}}(t)^T)\), \(R_{\theta \theta }(t)={\mathbb {E}}(\delta \theta (t)\delta \theta (t)^T)\)

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}{\mathbb {E}}(V(t))&=\frac{1}{2}Tr\left( \left( Q_1A+A^TQ_1\right) R_{\tilde{e}\tilde{e}}(t)\right) \nonumber \\&\quad +\frac{1}{2}Tr\left( \left( Q_2H+H^TQ_2\right) R_{\theta \theta }(t)\right) \nonumber \\&\quad +\frac{\lambda }{2}Tr\left( G^TQ_1GR_Y\right) +\frac{\tilde{\lambda }}{2}Tr\left( Q_2R_Z\right) \end{aligned}$$
(32)

where \(R_Y=(Y_1Y_1^T),R_Z={\mathbb {k}}(Z_1Z_1^T)\). We note more generally that if \(V(\tilde{e},\delta \theta )\) is any function of \(\tilde{e}\) and \(\delta \theta \), then

$$\begin{aligned}&\mathrm{d}V(\tilde{e},\delta \theta )=\left[ \left( \frac{\partial V}{\partial \tilde{e}}\right) ^T(A\tilde{e}+\tilde{W}\delta \theta )+\left( \frac{\partial V}{\partial \theta }\right) ^T(F\tilde{e}+H\delta \theta )\right] \mathrm{d}t\nonumber \\&\quad +\sum _{k\ge 1}^{}\frac{1}{k!}\left( \frac{\partial ^k V}{\partial \tilde{e}^k}\right) ^TG(t)^{\otimes k}Y^{\otimes k}_{N(t)+1}(-1)^k \mathrm{d}N(t)\nonumber \\&\quad +\sum _{k\ge 1}^{}\frac{1}{k!} \left( \frac{\partial ^kV}{\partial \theta ^k}\right) ^TZ^{\otimes k}_{\tilde{N}(t)+1}\mathrm{d}\tilde{N}(t) \end{aligned}$$
(33)

and hence,

$$\begin{aligned}&\frac{\mathrm{d}}{\mathrm{d}t}{\mathbb {E}}\left\{ V\left( \tilde{e}(t),\delta \theta (t)\right) \right\} \nonumber \\&\quad ={\mathbb {E}}\left( \left( \frac{\partial V}{\partial \tilde{e}}\right) ^TA \tilde{e}\right) +{\mathbb {E}}\left( \left( \frac{\partial V}{\partial \tilde{e}}\right) ^T\tilde{W}\delta \theta \right) \nonumber \\&\qquad +{\mathbb {E}}\left( \left( \frac{\partial V}{\partial \theta }\right) ^TF\tilde{e}\right) +{\mathbb {E}}\left( \left( \frac{\partial V}{\partial \theta }\right) ^TH\delta \theta \right) \nonumber \\&\qquad +\lambda \sum _{k\ge 1}^{}\frac{1}{k!}{\mathbb {E}} \left\{ \left( \frac{\partial ^k V}{\partial \tilde{e}^k}\right) ^T\right\} G^{\otimes k}\mu _k(Y)\nonumber \\&\qquad +\tilde{\lambda }\sum _{k\ge 1}^{}\frac{1}{k!}{\mathbb {E}} \left\{ \left( \frac{\partial ^k V}{\partial \theta ^k}\right) ^T\right\} \mu _k(Z) \end{aligned}$$
(34)

where \(\mu _k(Y)={\mathbb {E}}(Y_1^{\otimes k}), \mu _k(Z)={\mathbb {E}}(Z_1^{\otimes k})\). Equation (32) shows the explicit dependence of the rate of change in the average Lyapunov function on the Poisson rates \(\lambda ,\tilde{\lambda }\) as well as on the noise amplitude correlations matrices \(R_Y, R_Z\).

Remark 2

We can use (34) to arrive at an upper bound on \({\mathbb {E}} V(\tilde{e}(t),\delta \theta (t))\) which is a step toward proving stability.

Suppose that the Lyapunov function \(V(\tilde{e},\delta \theta )\) satisfies the inequalities

$$\begin{aligned} V(\tilde{e},\delta \theta )&\le a_0||\tilde{e}||^2+b_0||\delta \theta ||^2\nonumber \\ {}&\le K_0 V(\tilde{e},\delta \theta ) \end{aligned}$$
(35)

Suppose in addition, the partial derivatives of \(V(\tilde{e},\delta \theta )\) satisfy the inequalities

$$\begin{aligned}&\left\| \frac{\partial ^k V\left( \tilde{e},\delta \theta \right) }{\partial \tilde{e}^k}\right\| \le K_1\left( a_0||\tilde{e}||^2+b_0||\delta \theta ||^2\right) ^{1/2} \end{aligned}$$
(36a)
$$\begin{aligned}&\left\| \frac{\partial ^k V\left( \tilde{e},\delta \theta \right) }{\partial \theta ^k}\right\| \le K_2\left( a_0||\tilde{e}||^2+b_0||\delta \theta ||^2\right) ^{1/2}\nonumber \\ \end{aligned}$$
(36b)

Then,

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}{\mathbb {E}} V\left( \tilde{e},\delta \theta \right)&\le \alpha _1K_1{\mathbb {E}}\left[ \left( a_0||\tilde{e}||^2 +b_0||\delta \theta ||^2\right) ^{1/2}||\tilde{e}||\right] \nonumber \\&\quad +K_1\alpha _2{\mathbb {E}}\left[ \left( a_0||\tilde{e}||^2+b_0||\delta \theta ||^2\right) ^{1/2}||\delta \theta ||\right] \nonumber \\&\quad +K_2\alpha _3{\mathbb {E}} \left[ \left( a_0||\tilde{e}||^2+b_0||\delta \theta ||^2\right) ^{1/2}\right] \end{aligned}$$
(37)

where it is assumed that

$$\begin{aligned}&\lambda \sum \limits _{k\ge 1}^{}\frac{1}{k!}||G||^k|\mu _k(Y)<\infty \end{aligned}$$
(38a)
$$\begin{aligned}&\sum \limits _{k\ge 1}^{}\frac{1}{k!}|\mu _k(Z)|<\infty . \end{aligned}$$
(38b)

Thus

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}{\mathbb {E}} V(\tilde{e},\delta \theta )&\le a{\mathbb {E}}\left[ \sqrt{V\left( \tilde{e},\delta \theta \right) }\right] +b{\mathbb {E}}\left[ V\left( \tilde{e},\delta \theta \right) \right] \nonumber \\&\le a\left( {\mathbb {E}}V\left( \tilde{e},\delta \theta \right) \right) ^{1/2}+b{\mathbb {E}}\left[ V\left( \tilde{e},\delta \theta \right) \right] \end{aligned}$$
(39)

So letting

$$\begin{aligned} \varphi (t)={\mathbb {E}}[V(\tilde{e}(t),\delta \theta (t))], \end{aligned}$$
(40)

We get

$$\begin{aligned} \varphi '(t)\le a\sqrt{\varphi (t)}+b\varphi (t) \end{aligned}$$
(41)

Writing \(\sqrt{\varphi (t)}=\chi (t)\) gives

$$\begin{aligned} 2\chi \chi '\le a\chi +b\chi ^2 \end{aligned}$$
(42a)

or

$$\begin{aligned} \chi '\le \frac{a}{2}+\frac{b}{2}\chi . \end{aligned}$$
(42b)

giving

$$\begin{aligned} \chi (t)\le \int \limits _{0}^{t}e^{\frac{b}{2}(t-\tau )} \frac{a}{2}\mathrm{d}\tau =\frac{a}{b}\left( e^{\frac{bt}{2}-1}\right) \end{aligned}$$
(43)

So we can put a upper bound on the rate of growth of \(V(\tilde{e}(t),\delta \theta (t))\). Stability may be hard to prove but we can assert that \(\log {\mathbb {E}}[V(\tilde{e}(t),\delta \theta (t))]\) grows at most linearly with t.

3.2 Parameter estimation

Here, the problem involves computation of the probability density functional of the trajectory error process as a function of the parametric uncertainty. This expression may be used to obtain a maximum likelihood estimate of \(\delta \theta \) in the block processing format. The case of block processing parameter estimation based on discrete time measurements is also considered. We measure \(\tilde{e}(t)\) (i.e., \(q_d(t), \dot{q}_d(t),q(t),\dot{q}(t)\) or equivalently \(e(t), \dot{e}(t), \ddot{e}(t)\)) and let \(f_{\delta t}(w)\) denote the probability density of \(w(t)\mathrm{d}t\), i.e., of \(Y_{N(t)+1}\mathrm{d}N(t)\). Then from Eq. (16b), the approximate likelihood function of \(\delta \theta \) (assuming that it is a constant uncertainty) is given by

$$\begin{aligned} p(e(t):0\le t\le T\vert \delta \theta )&=\prod _{0\le t\le T}^{}f_{\delta t}(\delta \dot{e}(t)+K_pe(t)\delta t\nonumber \\&\quad +K_d\delta e(t)-W(t)\delta \theta \delta t) \end{aligned}$$
(44)

where \(\delta e(t)=e(t+\delta )-e(t), \delta \dot{e}(t)=\dot{e}(t+\delta )-\dot{e}(t), \delta \) being the time discretization step size and by \(\prod \limits _{0\le t\le T}^{}\psi (t)\) we actually mean \(\prod \limits _{0\le k\le [\frac{T}{\delta }]-1}{}\psi (k\delta )\). Note that

$$\begin{aligned} {\mathbb {E}} [e^{\iota \alpha ^TY_{N(t)+1}\mathrm{d}N(t)}]&=\lambda \mathrm{d}t{\mathbb {E}} e^{\iota \alpha ^T Y_1}+(1-\lambda \mathrm{d}t)\nonumber \\&=1+\lambda (\varPhi _Y(\alpha )-1)\mathrm{d}t \end{aligned}$$
(45)

where \(\varPhi _Y(\alpha )\) is the characteristic function of \(Y_1\).

Thus, we have an alternate description of the Likelihood function as a path integral:

$$\begin{aligned}&p(e(t):0\le t\le T\vert \delta \theta )\nonumber \\&\quad \propto \int \exp (\lambda \int _{0}^{T}(\varPhi _Y(\alpha (t))-1)\mathrm{d}t)\nonumber \\&\quad \times \exp (-\iota \int _{0}^{T}\alpha (t)^T(\mathrm{d}\dot{e}(t)+K_pe(t)\mathrm{d}t+K_de(t)\nonumber \\&\quad -W(t)\delta \theta \mathrm{d}t))\prod _{0\le t\le T}^{}\mathrm{d} \alpha (t) \end{aligned}$$
(46)

Alternately, if we measure \(\ddot{e}(t_k)\), \(e(t_k)\), \(\dot{e}(t_k)\), \(k=1,2,\ldots ,N\), then we can write the likelihood function for \(\delta \theta \) in the form

$$\begin{aligned}&p\left( e(t_k),\dot{e}(t_k), \ddot{e}(t_k), 1\le k\le N|\delta \theta \right) \nonumber \\&\quad =\int \times \exp \left( \lambda \sum _{k=1}^{N}\left( \varPhi _Y(\alpha _k)-1\right) \right) \nonumber \\&\qquad \times \exp \left( -\iota \sum _{k=1}^{N}\alpha _k^T\left( \ddot{e}(t_k)\right. \right. \nonumber \\&\qquad \left. \left. +\,K_pe(t_k)+K_d\dot{e}(t_k)-W(t_k)\delta \theta \right) \right) \prod _{k=1}^{N}\mathrm{d}\alpha _k \end{aligned}$$
(47)

Feynman path integrals are used extensively in quantum physics to calculate probabilities of events by solving the Schrodinger equation. In classical probability, they appear in the form of Kac formulas as the solution to the Heat equation with potentials. The maximization of this function of \(\delta \theta \) is easily implementable.

Note :  Equations  (45) and (46) are meant to express the probability law of the error process in path space aa a path integral. For this, we need the characteristic functional of the compound Poisson process

$$\begin{aligned} \xi (t)=\int \limits _{0}^{t}Y_{N(\tau )}\mathrm{d}N(\tau )=\sum \limits _{k=1}^{N(t)}Y_k \end{aligned}$$
(48)

We have \(\mathrm{d}\xi (t)=Y_{N(t)+1}\mathrm{d}N(t)\) and so

$$\begin{aligned} {\mathbb {E}}e^{\iota \alpha ^T\mathrm{d}\xi (t)}&={\mathbb {E}}\left( e^{\iota \alpha ^TY_1}\right) \lambda \mathrm{d}t+(1-\lambda \mathrm{d}t)\nonumber \\&=1+\lambda \mathrm{d}t\left( {\mathbb {E}}e^{\iota \alpha ^TY_1}-1\right) \end{aligned}$$
(49)

From which we declare that

$$\begin{aligned} {\mathbb {E}}e^{\int \limits _{0}^{T}\alpha (t)^T\mathrm{d}\xi (t)} =\exp \left( \lambda \int \limits _{0}^{T}\left( {\mathbb {E}}e^{\iota \alpha (t)^TY_1}-1\right) \mathrm{d}t\right) \end{aligned}$$
(50)

By infinite-dimensional Fourier inversion of the characteristic functional, we obtain the probability law as a path integral.

3.3 Time delay estimation in Lévy noise

Here, the problem considered is approximate time delay estimation from trajectory error measurements. The desired trajectory is read with some delay and the maximum likelihood estimation for the joint time delay and parameter uncertainty is constructed. \(q_d\) is known except for a time delay, i.e., the reference signal is \(q_d(t-T)\) where \(T=T_0+\delta T\) with \(T_0\) known but \(\delta T\) unknown and small. We write \(q_{d0}(t)\) in place of \(q_d(t-T_0)\). Then

$$\begin{aligned} q_d(t-T)&\approx q_d(t-T_0)-\dot{q}_d(t-T_0)\delta T\nonumber \\&=q_{d0}(t)-\dot{q}_{d0}(t)\delta T \end{aligned}$$
(51)

Then, it follows from Eq. (17) that

$$\begin{aligned} W(t)&=-M(q,\theta _0)^{-1}\left\{ \frac{\partial M}{\partial \theta }(q,\theta _0)\otimes (\ddot{q}_{d0}-\dddot{q}_{d0}\delta T)\right. \nonumber \\&\quad \left. +\,\frac{\partial N}{\partial \theta }(q,\dot{q},\theta _0)\right\} \nonumber \\&\quad \equiv W_0(t)+\delta T W_1(t) \end{aligned}$$
(52)

So

$$\begin{aligned} \ddot{e}(t)+K_pe(t)+K_d\dot{e}(t)&=(W_0(t)+\delta T W_1(t))\delta \theta \nonumber \\&\quad -Y_{N(t)+1}\frac{\mathrm{d}N(t)}{\mathrm{d}t} \end{aligned}$$
(53)

If the noise were white Gaussian then the maximum likelihood estimator of \(\delta T, \delta \theta \) would be

$$\begin{aligned} (\delta \hat{T}, \delta \hat{\theta })&= {\mathop {{{\mathrm{arg\,min}}}}\limits _{{\delta T, \delta \theta }}} \int _{0}^{T}||\ddot{e}(t)+K_pe(t)+K_d\dot{e}(t)\nonumber \\&\quad -W_0(t)\delta \theta -W_1(t)\delta T\delta \theta ||^2\mathrm{d}t \end{aligned}$$
(54)

We write \(\delta T\delta \theta =\delta \varphi \) and then setting the derivative of the above w.r.t \(\delta \theta \) and \(\delta \varphi \) to zero gives

$$\begin{aligned} \left[ \begin{array}{c} \dot{\delta }\hat{\theta }\\ \delta \hat{\varphi } \end{array}\right]&=\left[ \begin{array}{cc} \int _{0}^{T}W_0(t)^TW_0(t)dt &{} \int _{0}^{T}W_0(t)^TW_1(t)\mathrm{d}t\\ \int _{0}^{T}W_1(t)^TW_0(t)dt &{} \int _{0}^{T}W_1(t)^TW_1(t)\mathrm{d}t \end{array}\right] ^{-1}\nonumber \\&\quad \times \left[ \begin{array}{c} \int _{0}^{T}W_0(t)^T(\ddot{e}(t)+K_pe(t)+K_d\dot{e}(t))\mathrm{d}t\\ \int _{0}^{T}W_1(t)^T(\ddot{e}(t)+K_pe(t)+K_d\dot{e}(t))\mathrm{d}t \end{array}\right] \end{aligned}$$
(55)

In the compound Poisson case of Eq. (53), i.e., when the noise is

$$\begin{aligned} w(t)=Y_{N(t)+1}\frac{\mathrm{d}N(t)}{\mathrm{d}t} \end{aligned}$$
(56)

which is white but non-Gaussian, we have approximately

$$\begin{aligned} w(t)\varDelta t=Y_{N(t)+1}\varDelta N(t) \end{aligned}$$
(57)

where \(\varDelta N(t)=N(t+\varDelta t)-N(t)\) and

$$\begin{aligned} {\mathbb {E}} [e^{\alpha ^Tw(t)\varDelta t}]=\lambda \varDelta t {\mathbb {E}} e^{\alpha ^TY_1}+(1-\lambda \varDelta t) \end{aligned}$$
(58)

so that the probability density function of \(w(t)\varDelta t\) is given by

$$\begin{aligned} f_{w(t)\varDelta t}(W)=\delta (W)+\lambda \varDelta t(f_{y_1}(W)-\delta (W)\triangleq \varDelta f(W) \end{aligned}$$
(59)

The probability density functional of \(\{e(t),0\le t\le T\}\) is then approximately given by

$$\begin{aligned}&p(e(t), 0\le t \le T|\delta \theta , \delta T)\nonumber \\&\quad \approx \prod \limits _{t\in [0,T]}^{}\varDelta f(\ddot{e}(t)+K_pe(t)+K_d\dot{e}(t)\nonumber \\&\quad \quad -(W_0(t)+\delta T W_1(t))\delta \theta ) \end{aligned}$$
(60)

This is evaluated using a finite pulse approximate for the \(\delta \)-function and maximized with respect to \(\delta T\) and \(\delta \theta \) to obtain their maximum likelihood estimates.

Remark 3

In Sects. 3.2 and 3.3, we have pointed out how parameter uncertainties and time delays can be accounted for and even estimated in this jerk noise model. For example, we could consider an SDE

$$\begin{aligned} \mathrm{d}X(t)&=f(t,X(t),\theta )\mathrm{d}t\nonumber \\&\quad +\sum \limits _{k=1}^{p}g_k(t,X(t),X(t-\tau ),\theta )\mathrm{d}N_k(t) \end{aligned}$$
(61)

where \(\theta \) is the parametric uncertainty and \(\tau \) is the time delay. \(N_k(.),k=1,2,\ldots ,p\) are independent Poisson processes. X(.) is no longer a Markov process but as in [1], we can transform this SDE in to an infinite-dimensional Markovian SDE by introducing a vector

$$\begin{aligned} \xi (t)=\left[ \begin{array}{c} X(t)\\ X(t-\tau )\\ X(t-2\tau )\\ .\\ .\\ . \end{array}\right] \end{aligned}$$
(62)

yielding

$$\begin{aligned} \mathrm{d}\xi (t)=\tilde{f}(t,\xi (t),\theta )\mathrm{d}t+\sum \limits _{k=1}^{p} \tilde{g_k}(t,\xi (t),\theta )\mathrm{d}N_k(t) \end{aligned}$$
(63)

where

$$\begin{aligned} \tilde{f}(t,\xi (t),\theta )=\left[ \begin{array}{c} f(t,X(t),\theta )\\ f(t-\tau ,X(t-\tau ),\theta )\\ .\\ .\\ f(t-n\tau ,X(t-n\tau ),\theta )\\ .\\ . \end{array}\right] \end{aligned}$$
(64)

and likewise for \(\tilde{g_k}\). Then, \(\xi (t)\) is clearly a Markov process and the parameter \(\theta \) can be estimated by constructing the likelihood function of \(\xi (.)\) given \(\theta \). Markovian systems are more easily real-time implementable and the infinitesimal generator of a Markov process can directly be used to construct its probability distribution by solving the Chapman-Kolmogorov forward equation [20,21,22,23].

4 Simulation and numerical results

The differential equation

$$\begin{aligned} \ddot{e}(t)+K_p\dot{e}(t)+K_de(t)=W_0\delta \theta +\sigma _YY_{N_1(t)+1}\frac{\mathrm{d}N_1(t) }{\mathrm{d}t} \end{aligned}$$
(65)

that describes the tracking error evolution around a fixed point \(q(t)=q_0=q_{d0}\forall t\) and hence \(\dot{q}(t)=0,\ddot{q}(t)=0\forall t\) along with the parameter update equation

$$\begin{aligned} \delta \dot{\theta }(t)=F\tilde{e}(t)+H\delta \theta (t)+\sigma _ZZ_{N_2(t)+1}\mathrm{d}N_2(t) \end{aligned}$$
(66)

where

$$\begin{aligned} \tilde{e}(t)=\left( \begin{array}{cc}e(t)\\ \dot{e}(t)\end{array}\right) \end{aligned}$$

has been carried out in our experiments. We assumed that \(Y_k\) are constant vectors in \({\mathbb {R}}^2\) and \(Z_k\) are constant vectors in \({\mathbb {R}}^4\). In other words, the robot process noise is assumed to be a Poisson process and so is the noise process in the parameter update equation. Both the Poisson processes are assumed to be independent of each other. We could also assume that the \(Y_k's\) are independent and identically distributed (i.i.d.) random vectors and also the \(Z_k's\). In that case, our process noise and parameter update noise processes are compound Poisson processes which is a special case of a Lévy process. The state and parameter evolution Eqs. (21) and (66) can be expressed as

$$\begin{aligned} \mathrm{d}\xi (t)=P\xi (t)+G_1Y_1\mathrm{d}N_1(t)+G_2Z_1\mathrm{d}N_2(t) \end{aligned}$$
(67)

where

$$\begin{aligned} \xi (t)=\left( \begin{array}{c}\tilde{e}(t)\\ \delta \theta (t)\end{array}\right) , P=\left( \begin{array}{cc}A_1 &{} A_2\\ F &{} H\end{array}\right) \end{aligned}$$

where

The solution to the above state equation is expressed as a Poisson integral:

$$\begin{aligned} \xi (t)=\int _0^t\exp ((t-\tau )P)(G_1Y_1\mathrm{d}N_1(\tau )+G_2Z_1\mathrm{d}N_2(\tau )) \end{aligned}$$
(68)
Fig. 1
figure 1

Tracking error fluctuations in first angular position due to Poisson noise around a fixed position

Full size image
Fig. 2
figure 2

Tracking error fluctuations in second angular position due to Poisson noise around a fixed position

Full size image
Fig. 3
figure 3

Tracking error fluctuations in first angular velocity due to Poisson noise around a fixed position and zero velocity

Full size image
Fig. 4
figure 4

Tracking error fluctuations in second angular velocity due to Poisson noise around a fixed position and zero velocity

Full size image
Fig. 5
figure 5

Parametric error fluctuations in mass of link 1 (\(m_1\)) estimate due to Poisson noise around a fixed parameter estimate

Full size image
Fig. 6
figure 6

Parametric error fluctuations in mass of link 2 (\(m_2\)) estimate due to Poisson noise around a fixed parameter estimate

Full size image
Fig. 7
figure 7

Parametric error fluctuations in length of link 1 (\(l_1\)) estimate due to Poisson noise around a fixed parameter estimate

Full size image
Fig. 8
figure 8

Parametric error fluctuations in length of link 2 (\(l_2\)) estimate due to Poisson noise around a fixed parameter estimate

Full size image
Fig. 9
figure 9

Instantaneous Lyapunov tracking error cum parameter estimation error energy function

Full size image
Fig. 10
figure 10

Average Lyapunov tracking error cum parameter \(\delta \) estimation error energy function

Full size image

Plots of \(\xi (t)\) based on approximating this integral by a discrete stochastic sum are shown in Figs. 1, 2, 3, 4, 5, 6, 7 and 8. The plots show sudden spikes in the angular position and velocity tracking error. These spikes represent abrupt deviation of the error about the stable point \(q_0\) arising from the Poisson jerk noise. Figure 9 shows a plot of the Lyapunov energy function as a function of time. This function is defined as

$$\begin{aligned} V(t)&=\frac{1}{2}\tilde{e}(t)^TQ_{11}\tilde{e}(t)+\frac{1}{2}\delta \theta (t)^TQ_{22}\delta \theta (t)\nonumber \\&=\frac{1}{2}\xi (t)^TQ\xi (t) \end{aligned}$$
(69)

where

$$\begin{aligned} \xi (t)=\left( \begin{array}{cc}\tilde{e}(t)\\ \delta \theta (t)\end{array}\right) \end{aligned}$$

This energy plot is randomly fluctuating with spikes but the value around which these oscillations take place are roughly the same, namely the expected value of the Lyapunov energy function. Further, the oscillations appear to be bounded which show that the system is in some sense stochastically stable. Figure 10 confirms this fact by showing the expected value of V(t) against time. This plot is based on the exact formula

$$\begin{aligned} {\mathbb {E}}(V(t))=Tr(Q{\mathbb {E}}(\xi (t)\xi (t)^T)) \end{aligned}$$
(70)

where

$$\begin{aligned} {\mathbb {E}}\left( \xi (t)\xi (t)^T\right)&=\int _0^t\left( \exp (\tau P)\left( \lambda _1G_1Y_1Y_1^TG_1^T\right. \right. \nonumber \\&\quad \left. \left. +\,\lambda _2G_2Z_1Z_1^TG_2^T\right) \exp \left( \tau P^T\right) \right) \mathrm{d}\tau \end{aligned}$$
(71)

It is easily seen that since the eigenvalues of P all have negative real part, V(t) converges as \(t\rightarrow \infty \) to a constant and this constant represents the limiting average Lyapunov energy arising from random jerks. We also display hardware plots of the actual Phantom Omni Bundle angular position and velocity when the robot is driven by two torques, one a constant dc machine torque that balances the gravitational torque so that the angular positions of the links remain constant, two a jerk torque that comes from the hand operator. This jerk torque is generated by applying jerks at random time intervals. Alternately, if we are dealing with only a slave robot dynamics, the jerk torque comes from the environment in which the slave executes motion. The plots (Figs. 1, 2) of the angular position error \(q-q_d\) show rapid fluctuations concentrated over small time intervals followed by gaps during which the angular positions are constant. The plots (Figs. 3, 4) of the corresponding angular velocity error show larger spikes in the oscillations followed by gaps. This is as expected since the rate of change in small discontinuities can be very large. There is a strong match between the hardware and software generated plots which confirms that our theory based on the Ito differential rule for Poisson processes is valid in practical situations involving jerk forces applied to dynamical systems. It should be noted that a general nonlinear dynamical system excited by jerk noise can be modeled using the following SDE [24]

$$\begin{aligned} \mathrm{d}X(t)=f(t,X(t))\mathrm{d}t+\int _Eg(t,X(t),x)N(\mathrm{d}t,\mathrm{d}x)\nonumber \\ \end{aligned}$$
(72)

where \(N(t,\mathrm{d}x)\) is a space-time Poisson random field with intensity \(\lambda \mathrm{d}t \mathrm{d}F(x)\) and the integral above is taken over \(x\in E\). Such a space-time Poisson random field can be generated by taking a sequence of i.i.d. random variables \(X_n, n =1,2,\ldots \) having common distribution F(x), a Poisson process N(t) independent of the \(X_n's\) and defining for each Borel set A,

$$\begin{aligned} N(t,A,\omega )=\sum _{k=1}^{N(t)}\chi _{X_k\in A}(\omega ) \end{aligned}$$
(73)

where \(\chi _{X_k\in A}(\omega )\) is the random variable that equals one if \(X_k(\omega )\in A\) and zero otherwise. The process X(t) constructed in this way gives jerks with an amplitude dependent on the current time and state and is nonzero only if at time t, the Poisson process N(t) makes a jump such that the amplitude of the that jump is \(g(t,X(t),X_{N(t)+1})\). This is the most general form of a SDE driven by a compound Poisson process and the solution is a Markov process. It is an open problem as to how to simulate such a process using MATLAB.

Remark 4

Equation (72) suggests an example for computing approximately the mean, variance and higher moments of the output of an SDE driven by a Poisson field is as follows:

$$\begin{aligned} \mathrm{d}X(t)=f(t,X(t))\mathrm{d}t+\delta \int \limits _{E}^{}g(t,X(t),x)N(\mathrm{d}t,\mathrm{d}x) \end{aligned}$$
(74)

where \({\mathbb {E}} N(\mathrm{d}t,\mathrm{d}x)=\lambda \mathrm{d}t \mathrm{d}F(x)\) and \(\delta \) is a perturbation parameter introduced to show that the noise component is small. Let

$$\begin{aligned} X(t)=X_0(t)+\delta X_1(t)+\delta ^2 X_2(t)+\cdots . \end{aligned}$$
(75)

Then equating coefficients of \(\delta ^0,\delta ^1\) and \(\delta ^2\) gives

$$\begin{aligned} \frac{\mathrm{d} X_0(t)}{\mathrm{d}t}= & {} f(t,X_0(t)), \end{aligned}$$
(76a)
$$\begin{aligned} \mathrm{d}X_1(t)= & {} f'(t,X_0(t))X_1(t)\mathrm{d}t\nonumber \\&+\int g(t,X_0(t),x)N(\mathrm{d}t,\mathrm{d}x) \end{aligned}$$
(76b)
$$\begin{aligned} \mathrm{d}X_2(t)= & {} f'(t,X_0(t))X_2(t)\mathrm{d}t\nonumber \\&+\,\frac{1}{2}f''(t,X_0(t))X_1(t)^2\nonumber \\&+\,\int g'(t,X_0(t),x)X_1(t)N(\mathrm{d}t,\mathrm{d}x) \end{aligned}$$
(76c)

Thus if

$$\begin{aligned} \varPhi (t,s)=\exp \left( \int \limits _{s}^{t}f'\left( \tau ,X_0(\tau )\right) \right) \mathrm{d}\tau \end{aligned}$$
(77)

then

$$\begin{aligned} X_1(t)=\int \limits _{0\le s \le t,x\epsilon E}^{}\varPhi (t,s)g(s,X_0(s),x)N(\mathrm{d}s,\mathrm{d}x) \end{aligned}$$
(78a)

and

$$\begin{aligned} X_2(t)&=\frac{1}{2}\int \limits _{0\le s \le t}^{}\varPhi (t,s)f''(s,X_0(s))X_1(s)^2\mathrm{d}s\nonumber \\&\quad +\,\int \limits _{0\le s \le t,x\epsilon E}^{}\varPhi (t,s)g'(s,X_0(s),x)X_1(s)N(\mathrm{d}s,\mathrm{d}x) \end{aligned}$$
(78b)

\(\{X_0(t)\}\) is thus a non-random process,

$$\begin{aligned} {\mathbb {E}}(X_1(t))= & {} \lambda \int \limits _{0\le s \le t,x\epsilon E}^{}\varPhi (t,s)g(s,X_0(s),x)\mathrm{d}s\mathrm{d}F(x), \end{aligned}$$
(79a)
$$\begin{aligned} {\mathbb {E}}(X_1^2(t))= & {} \lambda \int \limits _{0\le s \le t,x\epsilon E}^{}\varPhi ^2(t,s)g^2(s,X_0(s),x)\mathrm{d}s\mathrm{d}F(x)\nonumber \\&+\,\lambda ^2\int \varPhi (t,s_1)\varPhi (t,s_2)g(s_1,X_0(s_1),x_1)\nonumber \\&\times \,g(s_2,X_0(s_2),x_2)\mathrm{d}s_1\mathrm{d}s_2\mathrm{d}F(x_1)\mathrm{d}F(x_2) \end{aligned}$$
(79b)
$$\begin{aligned} {\mathbb {E}}[X_2(t)]= & {} \frac{1}{2}\int \limits _{0\le s \le t}^{}\varPhi (t,s)f''(s,X_0(s)){\mathbb {E}}(X_1^2(s))\mathrm{d}s\nonumber \\&+\,\lambda \int \limits _{0\le s \le t,x\epsilon E}^{}\varPhi (t,s)g'(s,X_0(s),x){\mathbb {E}}(X_1(s))\mathrm{d}s\mathrm{d}F(x)\nonumber \\ \end{aligned}$$
(79c)

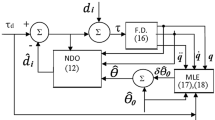
5 Lévy disturbance rejection using nonlinear filtering theory

Consider the general Lévy-driven dynamical system as a simplified version of Eq. (74):

$$\begin{aligned} \mathrm{d}\xi (t)=f(t,\xi (t))\mathrm{d}t+g(t,\xi (t))\mathrm{d}N(t) \end{aligned}$$
(80)

where N is a Poisson noise with rate \(\lambda \). We wish to eliminate the Poisson jerk N(t). For that, we must first measure \(\xi (t)\) or some output noise function of \(\xi (t)\) and then construct a real-time estimator \(\hat{\xi }(t)\) of \(\xi (t)\) based on these noisy observations and then estimate the disturbance N(t) using

$$\begin{aligned} \hat{N}(t)&=\int \limits _{0}^{t}\left( g\left( t,\hat{\xi }(t)\right) ^Tg\left( t,\hat{\xi }(t)\right) \right) ^{-1}g\left( t,\hat{\xi }(t)\right) ^T\nonumber \\&\quad \times \left( \mathrm{d}\hat{\xi }(t)-f\left( t,\hat{\xi }(t)\right) \mathrm{d}t\right) \end{aligned}$$
(81)

or equivalently,

$$\begin{aligned} \mathrm{d}\hat{N}(t)&=\left( g\left( t,\hat{\xi }(t)\right) ^Tg\left( t,\hat{\xi }(t)\right) \right) ^{-1}g\left( t,\hat{\xi }(t)\right) ^T \nonumber \\&\quad \times \left( \mathrm{d}\hat{\xi }(t)-f\left( t,\hat{\xi }(t)\right) \mathrm{d}t\right) \end{aligned}$$
(82)

To get \(\hat{\xi }(t)\), we consider a measurement output given by

$$\begin{aligned} \mathrm{d}z(t)=h(t,\xi (t))\mathrm{d}t+\sigma _v\mathrm{d}v(t) \end{aligned}$$
(83)

where v(t) is white Gaussian noise, i.e., \(v(t)=\frac{\mathrm{d}B(t)}{\mathrm{d}t}\) where B(t) is standard vector-valued Brownian motion. The real-time filter can be derives as follows:

For any function \(\phi (\xi )\) of \(\xi (t)\), define

$$\begin{aligned} \pi _t(\phi )={\mathbb {E}}(\phi (\xi (t))|z(s),s\le t) \end{aligned}$$
(84)

Then

$$\begin{aligned} \mathrm{d}\pi _t(\phi )=F_t(\phi )\mathrm{d}t+G_t(\phi )^T\mathrm{d}z(t) \end{aligned}$$
(85)

where \(F_t(\phi ),G_t(\phi )\) are measurable with respect to the \(\sigma -algeba\)

$$\begin{aligned} \sigma \{z(s):s\le t\}\triangleq z_t \end{aligned}$$
(86)

of the measurement up to time t.

The functions \(F_t(\phi )\) and \(G_t(\phi )\) can be calculated as follows: Let

$$\begin{aligned} \mathrm{d} C(t)=C(t)f(t)^T\mathrm{d}z(t),{C(0)=1} \end{aligned}$$
(87)

where \(f(t)=((f_k(t)))_{k=1}^d\) is a non-random vector-valued function of the same dimension as z(t). Then C(t) is measurable with respect to \(z_t\) and hence

$$\begin{aligned} {\mathbb {E}}[(\phi (\xi (t))-\pi _t(\phi ))C(t)]=0 \forall t \end{aligned}$$
(88)

(using the MMSE property of \(\pi _t(\phi )\)). Thus

$$\begin{aligned} \mathrm{d}{\mathbb {E}}[(\phi (\xi (t))-\pi _t(\phi ))C(t)]=0 \end{aligned}$$
(89)

or using Ito’s formula,

$$\begin{aligned}&{\mathbb {E}}[(\mathrm{d}\phi (\xi (t))-\mathrm{d}\pi _t(\phi ))C(t)]\nonumber \\&\quad +{\mathbb {E}}[(\phi (\xi (t))-\pi _t(\phi ))\mathrm{d}C(t)]\nonumber \\&\quad +{\mathbb {E}}[(\mathrm{d}\phi (\xi (t))-\mathrm{d}\pi _t(\phi ))\mathrm{d}C(t)]=0 \end{aligned}$$
(90)

and since f(t) is arbitrary, we infer that

$$\begin{aligned}&{\mathbb {E}}[(\mathrm{d}\phi (\xi (t))-\mathrm{d}\pi _t(\phi ))C(t)]=0, \end{aligned}$$
(91a)
$$\begin{aligned}&{\mathbb {E}}[(\phi (\xi (t))-\pi _t(\phi ))f(t)^T\mathrm{d}z(t)C(t)]\nonumber \\&\quad +{\mathbb {E}}[(\mathrm{d}\phi (\xi (t))-\mathrm{d}\pi _t(\phi ))(f(t)^T\mathrm{d}z(t))C(t)]=0\nonumber \\ \end{aligned}$$
(91b)

These imply

$$\begin{aligned}&{\mathbb {E}}[\mathrm{d}\phi (\xi (t))-\mathrm{d}\pi _t(\phi )|z_t]=0, \end{aligned}$$
(92a)
$$\begin{aligned}&{\mathbb {E}}[(\phi (\xi (t))-\pi _t(\phi ))\mathrm{d}z(t)|z_t]\nonumber \\&\quad +\,{\mathbb {E}}[(\mathrm{d}\phi (\xi (t))-\mathrm{d}\pi _t(\phi ))\mathrm{d}z(t)|z_t]=0 \end{aligned}$$
(92b)

Equation (92a) gives

$$\begin{aligned} {\mathbb {E}}[(\pounds _t\phi )(\xi (t))|z_t] -F_t(\phi )-G_t(\phi )^T{\mathbb {E}}[h(t,\xi (t))|z_t]=0, \end{aligned}$$
(93a)

while (92b) gives

$$\begin{aligned} {\mathbb {E}}[(\phi (\xi (t))-\pi _t(\phi ))h(t,\xi (t))|z_t]-\sigma _v^2G_t(\phi )=0 \end{aligned}$$
(93b)

or

$$\begin{aligned}&\pi _t(\pounds _t\phi )=F_t(\phi )+G_t(\phi )^T\pi _t(h_t), \end{aligned}$$
(94a)
$$\begin{aligned}&\pi _t(h_t\phi )-\pi _t(\phi )\pi _t(h_t)=\sigma _v^2G_t(\phi ) \end{aligned}$$
(94b)

Here \(\pounds _t\) is the generator of the Markov process \(\xi (t)\), i.e.,

$$\begin{aligned} \pounds _t\phi (\xi )=\triangledown \phi (\xi )^Tf(t,\xi )+\lambda (\phi (\xi +g(t,\xi ))-\phi (\xi )) \end{aligned}$$
(95)

These are the basic Kushner equations for dynamically estimating any function of the Markov process \(\xi (t)\) and as explained above can be applied to disturbance removal.

This idea of constructing a nonlinear dynamical filter can be found in [25]. The quantum non-commutative case discussed in [25] is a generalization of the classical commutative situation which we have discussed here.

Fig. 11
figure 11

Phantom Omni haptic device robot

Full size image
Fig. 12
figure 12

Schematic of two-link robot displaying where jerk acts and where non-random torque acts, \(q_1\) angle between first link and ground plane, \(q_2\) angle between first link and second link

Full size image

6 Experimentation and result

To validate our software simulation results, we have performed trajectory tracking experiments (without parametric uncertainties) on a Phantom Omni as shown in Fig. 11 by applying a desired machine torque in conjunction with a hand tremor torque and have plotted the angular position as a function of time. Figure 12 shows the schematic diagram of a two-link robot where Jerk acts and where non-random machine torque acts. The experiment is run in real time on MATLAB Simulink with the Phansim toolbox. Phansim toolbox builds up an interface on the top of the OpenHaptics Toolkit. The user can input torque or force to the box and can read the joint angle, gimbal angle and gimbal position [26]. Phantom Omni is a device which provides kinesthetic active force feedback on the x, y and z axes from the measurement of instantaneous position and velocity by use of joint optical encoders. IEEE.1394 Firewire port is used for the communication interface and allows real-time programming through class OpenHaptics based on C++. In this paper, real-time surface is implemented by MATLAB using Phansim toolbox [27]. Specifically, given a desired trajectory \(q_d(t)\), we have computed the torque to be given by

$$\begin{aligned} \tau _c(t)=M(q_d(t))q_d''(t)+N(q_d(t),q_d'(t)) \end{aligned}$$
(96)

and have added to this torque a feedback component

$$\begin{aligned} \tau _f(t)=M(q_d(t)(K_p(q_d(t)-q(t)+K_d(q_d'(t)-q'(t))) \end{aligned}$$
(97)

and a Lévy noise torque component w(t) given via the hand operator. The angular trajectory q(t) of the Omni Bundle satisfies the differential equation

$$\begin{aligned} M&(q(t))q''(t)+N(q(t),q'(t))\nonumber \\&=\tau _c(t)+\tau _f(t)+w(t)\nonumber \\&=M(q_d(t))(q_d''(t)+K_p(q_d(t)-q(t))\nonumber \\&\quad +K_d(q_d'(t)-q'(t)))+N(q_d(t),q_d'(t))+w(t) \end{aligned}$$
(98)

The actual parameters of the Phantom Omni are \(\theta _0=[m_1,m_2,l_1,l_2]\) where \(m_1= 0.035~\mathrm{kg}\), \(m_2= 0.1~\mathrm{kg}\), \(l_1= 0.135~\mathrm{m}\) and \(l_2= 0.135~\mathrm{m}\). The angular process q(t) traced out by the Omni Bundle has been measured and plotted along with the tracking error. Remarkable similarity with our software plots is seen which confirms the Poisson nature of the jerk noise. Figure 13 shows plots of the desired trajectory \(q_d\) for both the links which is a constant and the actual trajectory q which is spiky. The difference process is \(e=q-q_d\), and its first component is precisely Fig. 14. This Fig. 14 shows a plot of the hardware robot trajectory tracking error for link one with time when no machine torque has been applied and only tremor torque via the hand operator has been applied in the form of jerks at random time intervals. The resulting trajectory is a continuous sequence of spikes at random intervals. Figure 15 is a plot of the error trajectory for link 2 which is similar to that of link one and a formula for this spike process can be derived by linearizing the robot SDE about the stable operating point as we saw earlier. In fact the error process satisfies a linear second-order differential equation with compound Poisson differential input and the solution for the error process is a stochastic integral with respect to the Poisson process which can be represented as a shot noise process:

$$\begin{aligned} \int h(t,s)\mathrm{d}N(s)=\sum _{s_k<t}h(t,s_k) \end{aligned}$$
(99)
Fig. 13
figure 13

Hardware robot plot for both links of classical Phantom angular trajectory with constant desired trajectory and jerk noise given by hand operator

Full size image
Fig. 14
figure 14

Hardware robot plot for tracking error of link 1 with constant desired trajectory and jerk noise given by hand operator

Full size image
Fig. 15
figure 15

Hardware robot plot for tracking error of link 2 with constant desired trajectory and jerk noise given by hand operator

Full size image

where \(s_k\) are the arrival times of the Poisson process N(t) and \(h(t,s)=h(t-s)\) is the impulse response of the differential equation. If the pulse h(t) is sharp, then sharp spikes appear while if this pulse is spread out and smooth, then smoothened spikes appear. Further, Fig. 1 shows a plot of the error trajectory for link one angular position under the influence of compensated Poisson noise, i.e., Poisson noise with its mean subtracted out. Again we observe a sequence of spikes clustered at random intervals but now the spikes assume even negative values owing to the compensation, i.e., subtraction of the mean. The clustering can be explained by the fact that in the process of discretization of the dynamical system differential equations for simulation, a finite time step size is used which means that within the time interval of the discretization, the spikes increase and decay. This is in contrast to the hardware simulation where the step size is nearly zero. Figure 2 displays the software simulated angular position trajectory for link two. This is similar to that of link 1. Figure 16 displays the angular trajectory of the first link when a background sinusoidal torque through machines is applied and in addition, a hand tremor torque is applied. The plot is a beautiful display of a sinusoidal process with random spikes. It confirms the linearization approximation that when the noise is small, we can treat it as a first-order perturbation and apply linearized perturbation theory to compute the effect of random tremor on the trajectory. If the noise amplitude is larger, then it can interfere with the background sinusoidal trajectory but we have not considered this case which would require higher-order perturbation theory. The error plot for this case is Fig. 17. It shows that the error consists principally of jerk noise which means that if the noise were absent then the non-random trajectory is accurately tracked. Of course, some small amplitude negative valued spikes are also observed in this plot and that can be considered as errors in the tracking of the non-random component of the trajectory.

Fig. 16
figure 16

Hardware robot plot for link 1 of classical Phantom angular trajectory with sinusoidal desired trajectory and jerk noise given by hand operator

Full size image
Fig. 17
figure 17

Hardware robot plot for tracking error of link 1 with sinusoidal desired trajectory and jerk noise given by hand operator

Full size image

7 Conclusion

In this paper, we have considered a two-link robot with its kinetic energy specified by a quadratic function of its link angular momenta having coefficients dependent on the angle between the two links. The potential energy is gravitational, and apart from this there is a contribution to the Hamiltonian coming from the torque processes applied to the links. We have first set up the Lagrangian for this system and have included a Lévy noise component in the torque in the classical equations of motion. This Lévy noise component is determined by the jerks appearing in the motors and in the hand operator. The torque has been generated from a desired angular trajectory by incorporating parametric uncertainties in its computation. The tracking error process satisfies a linear second-order differential equation with Lévy noise driving input. Further, the parametric error update equation also satisfies a linear SDE with the tracking error appearing linearly in it. We club the trajectory tracking error, the tracking error rate of change and the parametric error into a single eight-component vector, and this satisfies a linear stochastic differential equation with Lévy noise input. The Lévy noise has been generated as a compound Poisson process. Stability of this system has been analyzed using stochastic Lyapunov theory. Plots of the angular position and velocity error, the parametric estimation error as well as the Lyapunov energy and its mean value have been obtained using MATLAB as well as by actually driving a Phantom Omni Bundle with jerks applied by the human operator and good agreement with the theoretical results have been obtained. A crucial ingredient in the theoretical analysis is the Ito formula for a Poisson process, and we have shown how this leads to results that differ drastically from the case when noise is white Gaussian with the standard Ito formula for the Brownian motion process being applicable.

Finally, we have illustrated how nonlinear filtering theory in the presence of measurement noise can be used for rejection of the Lévy noise component, i.e., we have addressed the disturbance rejection problem.