Flexural–flexural–extensional–torsional vibration analysis of composite spinning shafts with geometrical nonlinearity

Abstract

In this paper, nonlinear dynamics of an unbalanced composite spinning shaft are studied. Extensional–flexural–flexural–torsional equations of motion are derived via utilizing the three-dimensional constitutive relations of the material and Hamilton’s principle. The gyroscopic effects, rotary inertia and coupling due to material anisotropy are included, while the shear deformation is neglected. To analyze the rotor dynamic behavior, the full form of the equations without any simplification assumption (e.g., stretching or shortening assumption) is used. The method of multiple scales is applied to the discretized equations. An analytical expression as a function of the system parameters describing the forced vibration of a spinning composite shaft in the neighborhood of the primary resonance is obtained. The discretization is done with both one and two modes, and the results are compared. It is shown that although the excitation is tuned in the neighborhood of the first mode, one-mode discretization is not sufficient and it leads to inaccurate results. It shows the necessity of employing at least two modes in discretization due to the coupling in the equations. The effects of the external damping, eccentricity and the lamination angle on the vibration amplitude are investigated. In addition, the effect of the extensional–torsional coupling on the frequency response curves is investigated. To validate the perturbation results, numerical simulation is used.

Appendices

Appendix 1

$$\begin{aligned} \left\{ {\begin{array}{l} \sigma _{11} \\ \sigma _{22} \\ \sigma _{33} \\ \tau _{23} \\ \tau _{31} \\ \tau _{12} \\ \end{array}} \right\}= & {} \left[ {{\begin{array}{cccccc} {Q_{11} }&{} {Q_{12} }&{} {Q_{13} }&{} 0&{} 0&{} 0 \\ {Q_{12} }&{} {Q_{22} }&{} {Q_{23} }&{} 0&{} 0&{} 0 \\ {Q_{13} }&{} {Q_{23} }&{} {Q_{33} }&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} {Q_{44} }&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 0&{} {Q_{55} }&{} 0 \\ 0&{} 0&{} 0&{} 0&{} 0&{} {Q_{66} } \\ \end{array} }} \right] \left\{ {\begin{array}{l} \varepsilon _{11} \\ \varepsilon _{22} \\ \varepsilon _{33} \\ \gamma _{23} \\ \gamma _{31} \\ \gamma _{12} \\ \end{array}} \right\} \\ \left\{ {\begin{array}{l} \sigma _{xx} \\ \sigma _{\theta \theta } \\ \sigma _{rr} \\ \tau _{r\theta } \\ \tau _{xr} \\ \tau _{x\theta } \\ \end{array}} \right\}= & {} \left[ {{\begin{array}{cccccc} {\overline{Q} _{11} }&{} {\overline{Q} _{12} }&{} {\overline{Q} _{13} }&{} 0&{} 0&{} {\overline{Q} _{16} } \\ {\overline{Q} _{12} }&{} {\overline{Q} _{22} }&{} {\overline{Q} _{23} }&{} 0&{} 0&{} {\overline{Q} _{26} } \\ {\overline{Q} _{13} }&{} {\overline{Q} _{23} }&{} {\overline{Q} _{33} }&{} 0&{} 0&{} {\overline{Q} _{36} } \\ 0&{} 0&{} 0&{} {\overline{Q} _{44} }&{} {\overline{Q} _{45} }&{} 0 \\ 0&{} 0&{} 0&{} {\overline{Q} _{45} }&{} {\overline{Q} _{55} }&{} 0 \\ {\overline{Q} _{16} }&{} {\overline{Q} _{26} }&{} {\overline{Q} _{36} }&{} 0&{} 0&{} {\overline{Q} _{66} } \\ \end{array} }} \right] \left\{ {\begin{array}{l} \varepsilon _{xx} \\ \varepsilon _{\theta \theta } \\ \varepsilon _{rr} \\ \gamma _{r\theta } \\ \gamma _{xr} \\ \gamma _{x\theta } \\ \end{array}} \right\} \\ \left[ {\bar{{Q}}} \right]= & {} \left[ T \right] ^{-1}\left[ Q \right] \left[ T \right] ^{-T} \end{aligned}$$

where $\bar{{Q}}$ is the stiffness matrix of the layer in which

$$\begin{aligned} \left[ T \right]= & {} \left[ {{\begin{array}{cccccc} {m^{2}}&{} {n^{2}}&{} 0&{} 0&{} 0&{} {2mn} \\ {n^{2}}&{} {m^{2}}&{} 0&{} 0&{} 0&{} {-2mn} \\ 0&{} 0&{} 1&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} m&{} {-n}&{} 0 \\ 0&{} 0&{} 0&{} n&{} m&{} 0 \\ {-mn}&{} {mn}&{} 0&{} 0&{} 0&{} {m^{2}-n^{2}} \\ \end{array} }} \right] \\ m= & {} \cos \eta , n=\sin \eta \end{aligned}$$

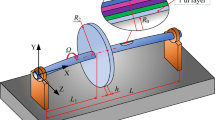
where $\eta$ is shown in Fig. 1.

$$\begin{aligned} Q_{11}= & {} \frac{E_1 }{1-\frac{\nu _{12}^2 E_2 }{E_1 }}, Q_{12} =\frac{E_2 \nu _{12} }{1-\frac{\nu _{12}^2 E_2 }{E_1 }},\\ Q_{22}= & {} \frac{E_2 }{1-\frac{\nu _{12}^2 E_2 }{E_1 }}, Q_{44} =G_{23} , Q_{55} =G_{13} , \\ Q_{66}= & {} G_{12} ,Q_{13} =Q_{23} =Q_{33} =0 \end{aligned}$$

Appendix 2

Derivation of equations of motion

Kinetic energy

$$\begin{aligned} T= & {} \frac{1}{2}I_0 \left( {\left( {\frac{\partial }{\partial t}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial t}v(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial t}w(s,t)} \right) ^{2}} \right) \\&+\frac{1}{2}\frac{I_2 \left( {\frac{\frac{\partial ^{2}}{\partial t\partial s}v(s,t)}{1+\frac{\partial }{\partial s}u(s,t)}-\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) \left( {\frac{\partial ^{2}}{\partial t\partial s}u(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) }{\left( {1+\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) ^{2}\left( {1+\frac{\left( {\frac{\partial }{\partial s}w(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}} \right) }\\&+\frac{1}{2}\frac{I_2 \left( {\frac{\frac{\partial ^{2}}{\partial t\partial s}w(s,t)}{\sqrt{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}}-\frac{0.5\left( {\frac{\partial }{\partial s}w(s,t)} \right) \left( {2\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) \left( {\frac{\partial ^{2}}{\partial t\partial s}u(s,t)} \right) +2\left( {\frac{\partial }{\partial s}v(s,t)} \right) \left( {\frac{\partial ^{2}}{\partial t\partial s}v(s,t)} \right) } \right) }{\sqrt{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}}} \right) ^{2}}{\left( {1+\frac{\left( {\frac{\partial }{\partial s}w(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}} \right) ^{2}}\\&+\frac{1}{2}I_{\mathrm{p}} \left( {\frac{\partial }{\partial s}\phi (s,t)} \right) ^{2}+I_{\mathrm{p}} \Omega \left( {\frac{\partial }{\partial s}\phi (s,t)} \right) +\frac{1}{2}I_{\mathrm{p}} \Omega ^{2}\\&+\frac{I_{\mathrm{p}} \left( {\frac{\partial }{\partial s}\phi (s,t)} \right) \left( {\frac{\frac{\partial ^{2}}{\partial t\partial s}v(s,t)}{1+\frac{\partial }{\partial s}u(s,t)}-\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) \left( {\frac{\partial ^{2}}{\partial t\partial s}u(s,t)} \right) }{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) \left( {\frac{\partial }{\partial s}w(s,t)} \right) }{\left( {1+\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) \sqrt{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}\sqrt{1+\frac{\left( {\frac{\partial }{\partial s}w(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}}}\\&+\frac{I_{\mathrm{p}} \Omega \left( {\frac{\frac{\partial ^{2}}{\partial t\partial s}v(s,t)}{1+\frac{\partial }{\partial s}u(s,t)}-\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) \left( {\frac{\partial ^{2}}{\partial t\partial s}u(s,t)} \right) }{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) \left( {\frac{\partial }{\partial s}w(s,t)} \right) }{\left( {1+\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) \sqrt{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}\sqrt{1+\frac{\left( {\frac{\partial }{\partial s}w(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}}}\\&+\frac{1}{2}\frac{I_{\mathrm{p}} \left( {\frac{\frac{\partial ^{2}}{\partial t\partial s}v(s,t)}{1+\frac{\partial }{\partial s}u(s,t)}-\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) \left( {\frac{\partial ^{2}}{\partial t\partial s}u(s,t)} \right) }{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) ^{2}}{\left( {1+\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) ^{2}}-\frac{1}{2}\frac{I_{\mathrm{p}} \left( {\frac{\frac{\partial ^{2}}{\partial t\partial s}v(s,t)}{1+\frac{\partial }{\partial s}u(s,t)}-\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) \left( {\frac{\partial ^{2}}{\partial t\partial s}u(s,t)} \right) }{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) ^{2}}{\left( {1+\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) ^{2}\left( {1+\frac{\left( {\frac{\partial }{\partial s}w(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}} \right) }\\ \end{aligned}$$

Potential energy

$$\begin{aligned} U= & {} \frac{1}{2}A_{11} \left( {\sqrt{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}w(s,t)} \right) ^{2}}-1} \right) ^{2}\\&+2B_{16} \left( {\sqrt{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}w(s,t)} \right) ^{2}}-1} \right) \\&\left( {\frac{\partial }{\partial s}\phi (s,t)+\frac{\left( {\frac{\frac{\partial ^{2}}{\partial s^{2}}v(s,t)}{1+\frac{\partial }{\partial s}u(s,t)}-\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) \left( {\frac{\partial ^{2}}{\partial s^{2}}u(s,t)} \right) }{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) \left( {\frac{\partial }{\partial s}w(s,t)} \right) }{\left( {1+\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) \sqrt{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}\sqrt{1+\frac{\left( {\frac{\partial }{\partial s}w(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}}}} \right) \\&+\frac{1}{2}D_{11} \left( {\begin{array}{l} \frac{\left( {\frac{\frac{\partial ^{2}}{\partial s^{2}}v(s,t)}{1+\frac{\partial }{\partial s}u(s,t)}-\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) \left( {\frac{\partial ^{2}}{\partial s^{2}}u(s,t)} \right) }{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) ^{2}}{\left( {1+\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) ^{2}\left( {1+\frac{\left( {\frac{\partial }{\partial s}w(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}} \right) }+ \\ \frac{\left( {\frac{\frac{\partial ^{2}}{\partial s^{2}}w(s,t)}{\sqrt{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}}-\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) \left( {\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) \left( {\frac{\partial ^{2}}{\partial s^{2}}u(s,t)} \right) +\left( {\frac{\partial }{\partial s}v(s,t)} \right) \left( {\frac{\partial ^{2}}{\partial s^{2}}v(s,t)} \right) } \right) }{\sqrt{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}}} \right) ^{2}}{\left( {1+\frac{\left( {\frac{\partial }{\partial s}w(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}} \right) ^{2}} \\ \end{array}} \right) \\&+\frac{1}{2}D_{66} \left( {\frac{\partial }{\partial s}\phi (s,t)+\frac{\left( {\frac{\frac{\partial ^{2}}{\partial s^{2}}v(s,t)}{1+\frac{\partial }{\partial s}u(s,t)}-\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) \left( {\frac{\partial ^{2}}{\partial s^{2}}u(s,t)} \right) }{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) \left( {\frac{\partial }{\partial s}w(s,t)} \right) }{\left( {1+\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) \sqrt{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}\sqrt{1+\frac{\left( {\frac{\partial }{\partial s}w(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}}}} \right) \end{aligned}$$

First the above kinetic and potential energies are expanded in Taylor series up to order four and then Hamilton’s principle

$$\begin{aligned} \int _{t_1 }^{t_2 } {\left[ {\delta (T)-\delta U} \right] \mathrm{d}t=0} \end{aligned}$$

is applied to obtain Eqs. (14)–(17).

Appendix 3

$$\begin{aligned} \Gamma _1= & {} \left( -\frac{9}{2}\beta _1 ^{2}\pi ^{4}\alpha \delta ^{2}+\frac{9}{2}I_{\mathrm{p}} \Omega \pi ^{6}\beta _1 +\frac{9}{2}\pi ^{8}D_{11} \alpha \delta ^{2}\right. \nonumber \\&\left. +\frac{3}{2}I_{\mathrm{p}} \Omega \pi ^{6}\beta _1 \delta ^{2}-\frac{3}{2}\beta _1 ^{2}\pi ^{4}\alpha +\frac{3}{2}\pi ^{8}D_{11} \alpha \right) A_{11}\nonumber \\ \Lambda _1= & {} \left( \frac{3}{4}\pi ^{8}D_{11} \alpha +\frac{9}{4}I_{\mathrm{p}} \Omega \pi ^{6}\beta _1 -\frac{9}{4}\beta _1 ^{2}\pi ^{4}\alpha ^{3}\right. \nonumber \\&\left. +\frac{3}{4}I_{\mathrm{p}} \Omega \pi ^{6}\beta _1 \alpha ^{2}+\frac{9}{4}\pi ^{8}D_{11} \alpha ^{3}-\frac{3}{4}\beta _1 ^{2}\pi ^{4}\alpha \right) A_{11} \end{aligned}$$

$$\begin{aligned} \Psi _1= & {} \left( \frac{3}{4}\beta _1 ^{2}\pi ^{4}\alpha -\frac{3}{4}\pi ^{8}D_{11} \alpha -\frac{3}{4}I_{\mathrm{p}} \Omega \pi ^{6}\beta _1 \right) A_{11} \\ \Phi _1= & {} -2\pi ^{4}D_{11} \alpha \beta _1 -I_{\mathrm{p}} ^{2}\Omega ^{2}\pi ^{4}\beta _1 \alpha \nonumber \\&+2\beta _1 ^{3}\alpha -\beta _1 ^{2}I_{\mathrm{p}} \Omega \pi ^{2}-\pi ^{6}D_{11} I_{\mathrm{p}} \Omega \\ \Gamma _2= & {} \left( \frac{9}{2}I_{\mathrm{p}} \Omega \pi ^{6}\beta _2 -\frac{3}{2}\beta _2 ^{2}\pi ^{4}\delta -\frac{9}{2}\beta _2 ^{2}\pi ^{4}\alpha ^{2}\delta \right. \nonumber \\&\left. +\frac{3}{2}I_{\mathrm{p}} \Omega \pi ^{6}\beta _2 \alpha ^{2}\!+\!\frac{9}{2}\pi ^{8}D_{11} \alpha ^{2}\delta \!+\!\frac{3}{2}\pi ^{8}D_{11} \delta \!\right) A_{11} \\ \Lambda _2= & {} \left( \frac{3}{4}I_{\mathrm{p}} \Omega \pi ^{6}\beta _2 \delta ^{2}+\frac{9}{4}I_{\mathrm{p}} \Omega \pi ^{6}\beta _2 \right. \nonumber \\&+\frac{3}{4}\pi ^{8}D_{11} \delta +\frac{9}{4}\pi ^{8}D_{11} \delta ^{3}-\frac{3}{4}\beta _2 ^{2}\pi ^{4}\delta \nonumber \\&\left. -\frac{9}{4}\beta _2 ^{2}\pi ^{4}\delta ^{3} \right) A_{11} \\ \Psi _2= & {} \left( {-\frac{3}{4}I_{\mathrm{p}} \Omega \pi ^{6}\beta _2 +\frac{3}{4}\beta _2 ^{2}\pi ^{4}\delta -\frac{3}{4}\pi ^{8}D_{11} \delta } \right) A_{11} \\ \Phi _2= & {} 2\beta _2 ^{3}\delta -\beta _2 ^{2}I_{\mathrm{p}} \Omega \pi ^{2}-I_{\mathrm{p}} ^{2}\Omega ^{2}\pi ^{4}\beta _2 \delta -\pi ^{6}D_{11} I_{\mathrm{p}} \Omega \nonumber \\&-2\pi ^{4}D_{11} \delta \beta _2 \end{aligned}$$

Appendix 4

$$\begin{aligned} \alpha= & {} -\frac{i\left( {\left( {-2\sqrt{\pi ^{8}\Omega ^{2}I_{\mathrm{p}} ^{2}\left( {\Omega ^{2}I_{\mathrm{p}} ^{2}+4D_{11} } \right) }+\left( {-4D_{11} -2\Omega ^{2}I_{\mathrm{p}} ^{2}} \right) \pi ^{4}} \right) ^{3/2}} \right) }{8I_{pp} \Omega \pi ^{6}D_{11} } \\&-\frac{i\left( {\pi ^{4}\left( {\Omega ^{2}I_{\mathrm{p}} ^{2}+D_{11} } \right) \sqrt{-2\sqrt{\pi ^{8}\Omega ^{2}I_{\mathrm{p}} ^{2}\left( {\Omega ^{2}I_{\mathrm{p}} ^{2}+4D_{11} } \right) }+\left( {-4D_{11} -2\Omega ^{2}I_{\mathrm{p}} ^{2}} \right) \pi ^{4}}} \right) }{2I_{pp} \Omega \pi ^{6}D_{11} } \\ \delta= & {} \frac{-i\left( {\left( {2\sqrt{\pi ^{8}\Omega ^{2}I_{\mathrm{p}} ^{2}\left( {\Omega ^{2}I_{\mathrm{p}} ^{2}+4D_{11} } \right) }+\left( {-4D_{11} -2\Omega ^{2}I_{\mathrm{p}} ^{2}} \right) \pi ^{4}} \right) ^{3/2}} \right) }{8I_{\mathrm{p}} \Omega \pi ^{6}D_{11} } \\&\frac{-i\left( {\pi ^{4}\left( {\Omega ^{2}I_{\mathrm{p}} ^{2}+D_{11} } \right) \sqrt{2\sqrt{\pi ^{8}\Omega ^{2}I_{\mathrm{p}} ^{2}\left( {\Omega ^{2}I_{\mathrm{p}} ^{2}+4D_{11} } \right) }+\left( {-4D_{11} -2\Omega ^{2}I_{\mathrm{p}} ^{2}} \right) \pi ^{4}}} \right) }{2I_{\mathrm{p}} \Omega \pi ^{6}D_{11} } \\ \zeta= & {} -\frac{3\left( {\frac{1}{3}\sqrt{9}\sqrt{\pi ^{2}\left( {\left( {A_{11} -4D_{66} } \right) ^{2}\pi ^{2}+\frac{1024}{9}B_{16} ^{2}} \right) }+\pi ^{2}\left( {A_{11} -4D_{66} } \right) } \right) }{16B_{16} \pi } \\ \lambda= & {} -\frac{3\left( {-\frac{1}{3}\sqrt{9}\sqrt{\pi ^{2}\left( {\left( {A_{11} -4D_{66} } \right) ^{2}\pi ^{2}+\frac{1024}{9}B_{16} ^{2}} \right) }+\pi ^{2}\left( {A_{11} -4D_{66} } \right) } \right) }{16B_{16} \pi } \\ \eta= & {} \frac{3\left( {\frac{1}{12}\sqrt{144}\sqrt{\left( {\left( {A_{11} -\frac{1}{4}D_{66} } \right) ^{2}\pi ^{2}+\frac{256}{9}B_{16} ^{2}} \right) \pi ^{2}}+\left( {A_{11} -\frac{1}{4}D_{66} } \right) \pi ^{2}} \right) }{32B_{16} \pi } \\ \mu= & {} \frac{3\left( {-\frac{1}{12}\sqrt{144}\sqrt{\left( {\left( {A_{11} -\frac{1}{4}D_{66} } \right) ^{2}\pi ^{2}+\frac{256}{9}B_{16} ^{2}} \right) \pi ^{2}}+\left( {A_{11} -\frac{1}{4}D_{66} } \right) \pi ^{2}} \right) }{32B_{16} \pi } \end{aligned}$$

Appendix 5

$$\begin{aligned}&U1_2 \left( {T_0 ,T_1 ,T_2 } \right) =\Pi 1_{u\phi 1} \left( {T_2 } \right) \hbox {e}^{-5i\beta _1 T_0 }\nonumber \\&\quad +\Pi 1_{u\phi 2} \left( {T_2 } \right) \hbox {e}^{-5i\beta _2 T_0 }+\Pi 1_{u\phi 3} \left( {T_2 } \right) \hbox {e}^{-3i\beta _1 T_0 }\nonumber \\&\quad +\Pi 1_{u\phi 4} \left( {T_2 } \right) \hbox {e}^{-3i\beta _2 T_0 } +\Pi 1_{u\phi 5} \left( {T_2 } \right) \hbox {e}^{-2i\beta _1 T_0 }\nonumber \\&\quad +\Pi 1_{u\phi 6} \left( {T_2 } \right) \hbox {e}^{-2i\beta _2 T_0 }+\Pi 1_{u\phi 7} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {-4\beta _2 +\beta _1 } \right) }\nonumber \\&\quad +\Pi 1_{u\phi 8} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {-\beta _2 +\beta _1 } \right) } +\Pi 1_{u\phi 9} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {-\beta _2 +4\beta _1 } \right) }\nonumber \\&\quad +\Pi 1_{u\phi 10} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 +\beta _1 } \right) }+\Pi 1_{u\phi 11} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 +4\beta _1 } \right) }\nonumber \\&\quad +\Pi 1_{u\phi 12} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {4\beta _2 +\beta _1 } \right) } +\Pi 1_{u\phi 13} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {-4\beta _2 +\beta _1 } \right) }\nonumber \\&\quad +\Pi 1_{u\phi 14} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {-\beta _2 +\beta _1 } \right) }+\Pi 1_{u\phi 15} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {-\beta _2 +4\beta _1 } \right) }\nonumber \\&\quad +\Pi 1_{u\phi 16} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 +\beta _1 } \right) } +\Pi 1_{u\phi 17} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 +4\beta _1 } \right) }\nonumber \\&\quad +\Pi 1_{u\phi 18} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {4\beta _2 +\beta _1 } \right) }+\Pi 1_{u\phi 19} \left( {T_2 } \right) \hbox {e}^{2i\beta _1 T_0 }\nonumber \\&\quad +\Pi 1_{u\phi 20} \left( {T_2 } \right) \hbox {e}^{2i\beta _2 T_0 }+\Pi 1_{u\phi 21} \left( {T_2 } \right) \hbox {e}^{3i\beta _1 T_0 } \\&\quad +\Pi 1_{u\phi 22} \left( {T_2 } \right) \hbox {e}^{3i\beta _2 T_0 }+\Pi 1_{u\phi 23} \left( {T_2 } \right) \hbox {e}^{5i\beta _1 T_0 }\nonumber \\&\quad +\Pi 1_{u\phi 24} \left( {T_2 } \right) \hbox {e}^{5i\beta _2 T_0 } \\&\varphi 2_2 \left( {T_0 ,T_1 ,T_2 } \right) =\Theta 2_{u\phi 1} \left( {T_2 } \right) \hbox {e}^{-5i\beta _1 T_0 }\nonumber \\&\quad +\Theta 2_{u\phi 2} \left( {T_2 } \right) \hbox {e}^{-5i\beta _2 T_0 }+\Theta 2_{u\phi 3} \left( {T_2 } \right) \hbox {e}^{-3i\beta _1 T_0 }\nonumber \\&\quad +\Theta 2_{u\phi 4} \left( {T_2 } \right) \hbox {e}^{-3i\beta _2 T_0 } +\Theta 2_{u\phi 5} \left( {T_2 } \right) \hbox {e}^{-2i\beta _1 T_0 }\nonumber \\&\quad +\Theta 2_{u\phi 6} \left( {T_2 } \right) \hbox {e}^{-2i\beta _2 T_0 } +\Theta 2_{u\phi 7} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {-4\beta _2 +\beta _1 } \right) }\nonumber \\&\quad +\Theta 2_{u\phi 8} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {-\beta _2 +\beta _1 } \right) }+\Theta 2_{u\phi 9} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {-\beta _2 +4\beta _1 } \right) }\nonumber \\&\quad +\Theta 2_{u\phi 10} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 +\beta _1 } \right) }+\Theta 2_{u\phi 11} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 +4\beta _1 } \right) }\nonumber \\&\quad +\Theta 2_{u\phi 12} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {4\beta _2 +\beta _1 } \right) } +\Theta 2_{u\phi 13} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {-4\beta _2 +\beta _1 } \right) }\nonumber \\&\quad +\Theta 2_{u\phi 14} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {-\beta _2 +\beta _1 } \right) }+\Theta 2_{u\phi 15} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {-\beta _2 +4\beta _1 } \right) }\nonumber \\&\quad +\Theta 2_{u\phi 16} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 +\beta _1 } \right) } +\Theta 2_{u\phi 17} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 +4\beta _1 } \right) }\nonumber \\&\quad +\Theta 2_{u\phi 18} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {4\beta _2 +\beta _1 } \right) }+\Theta 2_{u\phi 19} \left( {T_2 } \right) \hbox {e}^{2i\beta _1 T_0 }\nonumber \\&\quad +\Theta 2_{u\phi 20} \left( {T_2 } \right) \hbox {e}^{2i\beta _2 T_0 } +\Theta 2_{u\phi 21} \left( {T_2 } \right) \hbox {e}^{3i\beta _1 T_0 }\nonumber \\&\quad +\Theta 2_{u\phi 22} \left( {T_2 } \right) \hbox {e}^{3i\beta _2 T_0 }+\Theta 2_{u\phi 23} \left( {T_2 } \right) \hbox {e}^{5i\beta _1 T_0 }\nonumber \\&\quad +\Theta 2_{u\phi 24} \left( {T_2 } \right) \hbox {e}^{5i\beta _2 T_0 } \\ \end{aligned}$$

$$\begin{aligned}&U2_2 \left( {T_0 ,T_2 } \right) =\Pi 2_{u\phi 1} \left( {T_2 } \right) \hbox {e}^{-5i\beta _1 T_0 }\nonumber \\&\quad +\Pi 2_{u\phi 2} \left( {T_2 } \right) \hbox {e}^{-5i\beta _2 T_0 }+\Pi 2_{u\phi 3} \left( {T_2 } \right) \hbox {e}^{-3i\beta _1 T_0 }\nonumber \\&\quad +\Pi 2_{u\phi 4} \left( {T_2 } \right) \hbox {e}^{-3i\beta _2 T_0 } +\Pi 2_{u\phi 5} \left( {T_2 } \right) \hbox {e}^{-2i\beta _1 T_0 } \nonumber \\&\quad +\Pi 2_{u\phi 6} \left( {T_2 } \right) \hbox {e}^{-2i\beta _2 T_0 }+\Pi 2_{u\phi 7} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {-4\beta _2 +\beta _1 } \right) }\nonumber \\&\quad +\Pi 2_{u\phi 8} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {-\beta _2 +\beta _1 } \right) } +\Pi 2_{u\phi 9} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {-\beta _2 +4\beta _1 } \right) }\nonumber \\&\quad +\Pi 2_{u\phi 10} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 +\beta _1 } \right) }+\Pi 2_{u\phi 11} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 +4\beta _1 } \right) }\nonumber \\&\quad +\Pi 2_{u\phi 12} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {4\beta _2 +\beta _1 } \right) } \\&\quad +\Pi 2_{u\phi 13} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {-4\beta _2 +\beta _1 } \right) }+\Pi 2_{u\phi 14} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {-\beta _2 +\beta _1 } \right) }\nonumber \\&\quad +\Pi 2_{u\phi 15} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {-\beta _2 +4\beta _1 } \right) }+\Pi 2_{u\phi 16} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 +\beta _1 } \right) } \\&\quad +\Pi 2_{u\phi 17} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 +4\beta _1 } \right) }+\Pi 2_{u\phi 18} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {4\beta _2 +\beta _1 } \right) }\nonumber \\&\quad +\Pi 2_{u\phi 19} \left( {T_2 } \right) \hbox {e}^{2i\beta _1 T_0 }+\Pi 2_{u\phi 20} \left( {T_2 } \right) \hbox {e}^{2i\beta _2 T_0 } \\&\quad +\Pi 2_{u\phi 21} \left( {T_2 } \right) \hbox {e}^{3i\beta _1 T_0 }+\Pi 2_{u\phi 22} \left( {T_2 } \right) \hbox {e}^{3i\beta _2 T_0 }\nonumber \\&\quad +\Pi 2_{u\phi 23} \left( {T_2 } \right) \hbox {e}^{5i\beta _1 T_0 }+\Pi 2_{u\phi 24} \left( {T_2 } \right) \hbox {e}^{5i\beta _2 T_0 } \\&\varphi 1_2 \left( {T_0 ,T_2 } \right) =\Theta 1_{u\phi 1} \left( {T_2 } \right) \hbox {e}^{-5i\beta _1 T_0 }+\Theta 1_{u\phi 2} \left( {T_2 } \right) \hbox {e}^{-5i\beta _2 T_0 }\nonumber \\&\quad +\Theta 1_{u\phi 3} \left( {T_2 } \right) \hbox {e}^{-3i\beta _1 T_0 }+\Theta 1_{u\phi 4} \left( {T_2 } \right) \hbox {e}^{-3i\beta _2 T_0 } \\&\quad +\Theta 1_{u\phi 5} \left( {T_2 } \right) \hbox {e}^{-2i\beta _1 T_0 }+\Theta 1_{u\phi 6} \left( {T_2 } \right) \hbox {e}^{-2i\beta _2 T_0 }\nonumber \\&\quad +\Theta 1_{u\phi 7} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {-4\beta _2 +\beta _1 } \right) }+\Theta 1_{u\phi 8} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {-\beta _2 +\beta _1 } \right) } \\&\quad +\Theta 1_{u\phi 9} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {-\beta _2 +4\beta _1 } \right) }+\Theta 1_{u\phi 10} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 +\beta _1 } \right) }\nonumber \\&\quad +\Theta 1_{u\phi 11} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 +4\beta _1 } \right) }+\Theta 1_{u\phi 12} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {4\beta _2 +\beta _1 } \right) } \\&\quad +\Theta 1_{u\phi 13} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {-4\beta _2 +\beta _1 } \right) }+\Theta 1_{u\phi 14} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {-\beta _2 +\beta _1 } \right) }\nonumber \\&\quad +\Theta 1_{u\phi 15} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {-\beta _2 +4\beta _1 } \right) }+\Theta 1_{u\phi 16} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 +\beta _1 } \right) } \\&\quad +\Theta 1_{u\phi 17} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 +4\beta _1 } \right) }+\Theta 1_{u\phi 18} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {4\beta _2 +\beta _1 } \right) }\nonumber \\&\quad +\Theta 1_{u\phi 19} \left( {T_2 } \right) \hbox {e}^{2i\beta _1 T_0 }+\Theta 1_{u\phi 20} \left( {T_2 } \right) \hbox {e}^{2i\beta _2 T_0 }\nonumber \\&\quad +\Theta 1_{u\phi 21} \left( {T_2 } \right) \hbox {e}^{3i\beta _1 T_0 } \\&\quad +\Theta 1_{u\phi 22} \left( {T_2 } \right) \hbox {e}^{3i\beta _2 T_0 }+\Theta 1_{u\phi 23} \left( {T_2 } \right) \hbox {e}^{5i\beta _1 T_0 }\\&\quad +\Theta 1_{u\phi 24} \left( {T_2 } \right) \hbox {e}^{5i\beta _2 T_0 } \\ \end{aligned}$$

$$\begin{aligned}&V1_2 (T_0 ,T_2 )=\Pi 1_{vw1} \hbox {e}^{-iT_0 \left( {\beta _1 -\beta _{32} } \right) }\nonumber \\&\quad +\Pi 1_{vw2} \hbox {e}^{-iT_0 \left( {\beta _1 +\beta _{32} } \right) }\nonumber \\&\quad +\Pi 1_{vw3} \hbox {e}^{-iT_0 \left( {\beta _1 -\beta _\phi } \right) }+\Pi 1_{vw4} \hbox {e}^{-iT_0 \left( {\beta _1 +\beta _\phi } \right) } \\&\quad +\Pi 1_{vw5} \hbox {e}^{-iT_0 \left( {4\beta _1 -\beta _{31} } \right) }+\Pi 1_{vw6} \hbox {e}^{-iT_0 \left( {\beta _2 -\beta _{32} } \right) }\nonumber \\&\quad +\Pi 1_{vw7} \hbox {e}^{-iT_0 \left( {\beta _2 +\beta _{32} } \right) }+\Pi 1_{vw8} \hbox {e}^{-iT_0 \left( {\beta _2 -\beta _\phi } \right) }\nonumber \\&\quad +\Pi 1_{vw9} \hbox {e}^{-iT_0 \left( {\beta _2 +\beta _\phi } \right) }+\Pi 1_{vw10} \hbox {e}^{-iT_0 \left( {4\beta _2 -\beta _{2\phi } } \right) } \\&\quad +\Pi 1_{vw11} \hbox {e}^{-iT_0 \left( {-\beta _{31} +4\beta _2 } \right) }+\Pi 1_{vw12} \hbox {e}^{-iT_0 \left( {\beta _{31} +4\beta _1 } \right) }\nonumber \\&\quad +\Pi 1_{vw13} \hbox {e}^{-iT_0 \left( {\beta _{31} +4\beta _2 } \right) }+\Pi 1_{vw14} \hbox {e}^{-iT_0 \left( {-\beta _{2\phi } +4\beta _1 } \right) } \\&\quad +\Pi 1_{vw15} \hbox {e}^{-iT_0 \left( {\beta _{2\phi } +4\beta _1 } \right) }+\Pi 1_{vw16} \hbox {e}^{-iT_0 \left( {\beta _{2\phi } +4\beta _2 } \right) }\nonumber \\&\quad +\Pi 1_{vw17} \hbox {e}^{iT_0 \left( {\beta _1 -\beta _{32} } \right) }+\Pi 1_{vw18} \hbox {e}^{iT_0 \left( {\beta _1 +\beta _{32} } \right) } \\&\quad +\Pi 1_{vw19} \hbox {e}^{iT_0 \left( {\beta _1 -\beta _\phi } \right) }+\Pi 1_{vw20} \hbox {e}^{iT_0 \left( {\beta _1 +\beta _\phi } \right) }\nonumber \\&\quad +\Pi 1_{vw21} \hbox {e}^{iT_0 \left( {4\beta _1 -\beta _{31} } \right) }+\Pi 1_{vw22} \hbox {e}^{iT_0 \left( {\beta _2 -\beta _{32} } \right) } \\&\quad +\Pi 1_{vw23} \hbox {e}^{iT_0 \left( {\beta _2 +\beta _{32} } \right) }+\Pi 1_{vw24} \hbox {e}^{iT_0 \left( {\beta _2 -\beta _\phi } \right) }\nonumber \\&\quad +\Pi 1_{vw25} \hbox {e}^{iT_0 \left( {\beta _2 +\beta _\phi } \right) }+\Pi 1_{vw26} \hbox {e}^{iT_0 \left( {4\beta _2 -\beta _{2\phi } } \right) }\nonumber \\&\quad +\Pi 1_{vw27} \hbox {e}^{iT_0 \left( {-\beta _{31} +4\beta _2 } \right) }+\Pi 1_{vw28} \hbox {e}^{iT_0 \left( {\beta _{31} +4\beta _1 } \right) } \\&\quad +\Pi 1_{vw29} \hbox {e}^{iT_0 \left( {\beta _{31} +4\beta _2 } \right) }+\Pi 1_{vw30} \hbox {e}^{iT_0 \left( {-\beta _{2\phi } +4\beta _1 } \right) }\nonumber \\&\quad +\Pi 1_{vw31} \hbox {e}^{iT_0 \left( {\beta _{2\phi } +4\beta _1 } \right) }+\Pi 1_{vw32} \hbox {e}^{iT_0 \left( {\beta _{2\phi } +4\beta _2 } \right) } \\ \end{aligned}$$

$$\begin{aligned}&W1_2 (T_0 ,T_2 )=\Theta 1_{vw1} \hbox {e}^{-iT_0 \left( {\beta _1 -\beta _{32} } \right) }\nonumber \\&\quad +\Theta 1_{vw2} \hbox {e}^{-iT_0 \left( {\beta _1 +\beta _{32} } \right) }+\Theta 1_{vw3} \hbox {e}^{-iT_0 \left( {\beta _1 -\beta _\phi } \right) }\nonumber \\&\quad +\Theta 1_{vw4} \hbox {e}^{-iT_0 \left( {\beta _1 +\beta _\phi } \right) }+\Theta 1_{vw5} \hbox {e}^{-iT_0 \left( {4\beta _1 -\beta _{31} } \right) } \\&\quad +\Theta 1_{vw6} \hbox {e}^{-iT_0 \left( {\beta _2 -\beta _{32} } \right) }+\Theta 1_{vw7} \hbox {e}^{-iT_0 \left( {\beta _2 +\beta _{32} } \right) }\nonumber \\&\quad +\Theta 1_{vw8} \hbox {e}^{-iT_0 \left( {\beta _2 -\beta _\phi } \right) }+\Theta 1_{vw9} \hbox {e}^{-iT_0 \left( {\beta _2 +\beta _\phi } \right) }\nonumber \\&\quad +\Theta 1_{vw10} \hbox {e}^{-iT_0 \left( {4\beta _2 -\beta _{2\phi } } \right) } \\&\quad +\Theta 1_{vw11} \hbox {e}^{-iT_0 \left( {-\beta _{31} +4\beta _2 } \right) }+\Theta 1_{vw12} \hbox {e}^{-iT_0 \left( {\beta _{31} +4\beta _1 } \right) }\nonumber \\&\quad +\Theta 1_{vw13} \hbox {e}^{-iT_0 \left( {\beta _{31} +4\beta _2 } \right) }+\Theta 1_{vw14} \hbox {e}^{-iT_0 \left( {-\beta _{2\phi } +4\beta _1 } \right) } \\&\quad +\Theta 1_{vw15} \hbox {e}^{-iT_0 \left( {\beta _{2\phi } +4\beta _1 } \right) }\nonumber \\&\quad +\Theta 1_{vw16} \hbox {e}^{-iT_0 \left( {\beta _{2\phi } +4\beta _2 } \right) }+\Theta 1_{vw17} \hbox {e}^{iT_0 \left( {\beta _1 -\beta _{32} } \right) }\nonumber \\&\quad +\Theta 1_{vw18} \hbox {e}^{iT_0 \left( {\beta _1 +\beta _{32} } \right) }+\Theta 1_{vw19} \hbox {e}^{iT_0 \left( {\beta _1 -\beta _\phi } \right) } \\&\quad +\Theta 1_{vw20} \hbox {e}^{iT_0 \left( {\beta _1 +\beta _\phi } \right) }+\Theta 1_{vw21} \hbox {e}^{iT_0 \left( {4\beta _1 -\beta _{31} } \right) }\nonumber \\&\quad +\Theta 1_{vw22} \hbox {e}^{iT_0 \left( {\beta _2 -\beta _{32} } \right) }+\Theta 1_{vw23} \hbox {e}^{iT_0 \left( {\beta _2 +\beta _{32} } \right) }\nonumber \\&\quad +\Theta 1_{vw24} \hbox {e}^{iT_0 \left( {\beta _2 -\beta _\phi } \right) } \\&\quad +\Theta 1_{vw25} \hbox {e}^{iT_0 \left( {\beta _2 +\beta _\phi } \right) }+\Theta 1_{vw26} \hbox {e}^{iT_0 \left( {4\beta _2 -\beta _{2\phi } } \right) }\nonumber \\&\quad +\Theta 1_{vw27} \hbox {e}^{iT_0 \left( {-\beta _{31} +4\beta _2 } \right) }+\Theta 1_{vw28} \hbox {e}^{iT_0 \left( {\beta _{31} +4\beta _1 } \right) }\nonumber \\&\quad +\Theta 1_{vw29} \hbox {e}^{iT_0 \left( {\beta _{31} +4\beta _2 } \right) } +\Theta 1_{vw30} \hbox {e}^{iT_0 \left( {-\beta _{2\phi } +4\beta _1 } \right) }\nonumber \\&\quad +\Theta 1_{vw31} \hbox {e}^{iT_0 \left( {\beta _{2\phi } +4\beta _1 } \right) }+\Theta 1_{vw32} \hbox {e}^{iT_0 \left( {\beta _{2\phi } +4\beta _2 } \right) } \\ \end{aligned}$$

$$\begin{aligned}&V2_2 \left( {T_0 ,T_2 } \right) =\Pi 2_{vw1} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _1 -\beta _{31} } \right) }\\&\quad +\Pi 2_{vw2} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _1 +\beta _{u1} } \right) }\nonumber \\&\quad +\Pi 2_{vw3} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _1 -\beta _{\phi 2} } \right) } \\&\quad +\Pi 2_{vw4} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _1 +\beta _{\phi 2} } \right) }\nonumber \\&\quad +\Pi 2_{vw5} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 -\beta _{u1} } \right) }\\&\quad +\Pi 2_{vw6} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 +\beta _{u1} } \right) }\nonumber \\&\quad +\Pi 2_{vw7} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 -\beta _{\phi 2} } \right) } \\&\quad +\Pi 2_{vw8} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 +\beta _{\phi 2} } \right) }\nonumber \\&\quad +\Pi 2_{vw9} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _1 -\beta _{u1} } \right) }\nonumber \\&\quad +\Pi 2_{vw10} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _1 +\beta _{u1} } \right) }\nonumber \\&\quad +\Pi 2_{vw11} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _1 -\beta _{\phi 2} } \right) } \\&\quad +\Pi 2_{vw12} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _1 +\beta _{\phi 2} } \right) }\nonumber \\&\quad +\Pi 2_{vw13} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 -\beta _{u1} } \right) }\nonumber \\&\quad +\Pi 2_{vw14} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 +\beta _{u1} } \right) }\nonumber \\&\quad +\Pi 2_{vw15} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 -\beta _{\phi 2} } \right) } \\&\quad +\Pi 2_{vw16} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 +\beta _{\phi 2} } \right) } \\&W2_2 \left( {T_0 ,T_2 } \right) =\Theta 2_{vw1} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _1 -\beta _{31} } \right) }\nonumber \\&\quad +\Theta 2_{vw2} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _1 +\beta _{u1} } \right) }+\Theta 2_{vw3} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _1 -\beta _{\phi 2} } \right) } \\&\quad +\Theta 2_{vw4} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _1 +\beta _{\phi 2} } \right) }+\Theta 2_{vw5} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 -\beta _{u1} } \right) }\nonumber \\&\quad +\Theta 2_{vw6} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 +\beta _{u1} } \right) }+\Theta 2_{vw7} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 -\beta _{\phi 2} } \right) } \\&\quad +\Theta 2_{vw8} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 +\beta _{\phi 2} } \right) }+\Theta 2_{vw9} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _1 -\beta _{u1} } \right) }\nonumber \\&\quad +\Theta 2_{vw10} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _1 +\beta _{u1} } \right) }+\Theta 2_{vw11} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _1 -\beta _{\phi 2} } \right) } \\&\quad +\Theta 2_{vw12} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _1 +\beta _{\phi 2} } \right) }+\Theta 2_{vw13} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 -\beta _{u1} } \right) }\nonumber \\&\quad +\Theta 2_{vw14} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 +\beta _{u1} } \right) }+\Theta 2_{vw15} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 -\beta _{\phi 2} } \right) } \\&\quad +\Theta 2_{vw16} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 +\beta _{\phi 2} } \right) } \\ \end{aligned}$$