Abstract
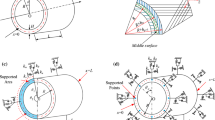
The geometrically nonlinear forced vibration response of non-continuous elastic-supported laminated composite thin cylindrical shells is investigated in this paper. Two kinds of non-continuous elastic supports are simulated by using artificial springs, which are point and arc constraints, respectively. By using a set of Chebyshev polynomials as the admissible displacement function, the nonlinear differential equation of motion of the shell subjected to periodic radial point loading is obtained through the Lagrange equations, in which the geometric nonlinearity is considered by using Donnell’s nonlinear shell theory. Then, these equations are solved by using the numerical method to obtain nonlinear amplitude–frequency response curves. The numerical results illustrate the effects of spring stiffness and constraint range on the nonlinear forced vibration of points-supported and arcs-supported laminated composite cylindrical shells. The results reveal that the geometric nonlinearity of the shell can be changed by adjusting the values of support stiffness and distribution areas of support, and the values of circumferential and radial stiffness have a more significant influence on amplitude–frequency response than the axial and torsional stiffness.








Similar content being viewed by others
Abbreviations
- \({{\varvec{A}}}_{ij} \) :
-
The stretching stiffness coefficients
- \({\varvec{B}}_{ij} \) :
-
The coupling stiffness coefficients
- \({\varvec{C}}\) :
-
Damping matrix
- \({\varvec{D}}_{ij} \) :
-
The bending stiffness coefficients
- \(E_1,E_2\) :
-
Yong’s modulus in the principal directions
- Ei :
-
The error of the non-dimension y-coordinate of \(\hbox {NT}=i\) with respect to \(\hbox {NT}=6\)
- \({\varvec{F}}(t)\) :
-
The point harmonic excitation
- \(G_{12} \) :
-
Moduli of rigidity
- H :
-
Thickness of the shell
- \({\varvec{K}}, {\varvec{K}}_{\mathrm{spr}}\) :
-
Stiffness matrix, spring stiffness matrix
- L :
-
Length of the shell
- \({\varvec{M}}\) :
-
Mass matrix
- \({\varvec{M}}_{x},{\varvec{M}}_{\theta },{\varvec{M}}_{x\theta }\) :
-
The moments of the in-plane stresses
- N :
-
The number of terms for circumferential wave
- \({\varvec{N}}_x,{\varvec{N}}_\theta ,{\varvec{N}}_{x\theta }\) :
-
The force of the in-plane stresses
- NA:
-
The number of supported points
- NS:
-
The number of supported arcs
- NT:
-
The number of terms for Chebyshev polynomials
- \({\varvec{Q}}\) :
-
Plane stresses–strain matrix
- \({\overline{{\varvec{Q}}}} \) :
-
Transformation stiffness matrix
- \({\varvec{Q}}^{\prime }\) :
-
The nonlinear vector
- R :
-
Radius of the shell
- \({\varvec{T}}_{\mathrm{s}} \) :
-
Transformation matrix
- T :
-
Kinetic energy
- \({\varvec{T}}_m^*\left( \xi \right) \) :
-
The admissible displacement functions
- \(U_\varepsilon , U_{\mathrm{spr}} \) :
-
Strain energy, potential energy
- \(\bar{{{\varvec{U}}}}, \bar{{{\varvec{V}}}}, \bar{{{\varvec{W}}}}\) :
-
The mode vector satisfying a boundary condition
- \(a_m , b_m , c_m \) :
-
The unknown corresponding coefficients
- \(f_0 \) :
-
The amplitude of harmonic excitation
- \(k_{u} ,k_{v} ,k_{w} ,k_{\theta }\) :
-
Stiffness of axial, circumferential, radial, rotational spring per unit arc length
- \({k}^{\prime }_u ,{k}^{\prime }_v ,{k}^{\prime }_w ,{k}^{\prime }_\theta \) :
-
Stiffness of axial, circumferential, radial, rotational spring
- n :
-
The circumferential wave number
- \({\varvec{q}}\) :
-
The generalized coordinates
- t :
-
Time
- u, v, w :
-
Displacement in the x, \(\theta \), z directions
- \(\alpha \) :
-
The total length of supported arcs
- \(\beta \) :
-
Angular orientation of fibers
- \(\varepsilon _x,\varepsilon _\theta ,\gamma _{x\theta }\) :
-
The strains of the shell
- \(\theta \) :
-
The constraint radian
- \(\theta _s,\theta '_s\) :
-
The starting and ending radian of the sth arcs
- \(\kappa _x,\kappa _\theta ,\kappa _{x\theta }\) :
-
The curvature of the shell
- \(\mu _{12},\mu _{21}\) :
-
Poisson’s ratios
- \(\xi \) :
-
The non-dimensional axial coordinate
- \(\rho \) :
-
Mass density
- \(\sigma _{\mathrm{x}} ,\sigma _{\mathrm{y}} ,\tau _{\mathrm{xy}}\) :
-
The stresses of the shell
- \(\omega \) :
-
The frequency of harmonic excitation
- \(\omega ^{*}\) :
-
The non-dimensional natural frequency
- \(\omega _d\) :
-
The natural frequency of the shell
References
Leissa, A.W., Nordgren, R.P.: Vibration of shells. J. Appl. Mech. 41(2), 544 (1993)
Qatu, M.S.: Recent research advances in the dynamic behavior of shells: 1989–2000, Part 1: Laminated composite shells. Appl. Mech. Rev. 55(5), 325–350 (2002)
Qatu, M.S., Sullivan, R.W., Wang, W.: Recent research advances on the dynamic analysis of composite shells: 2000–2009. Compos. Struct. 93(1), 14–31 (2010)
Lam, K.Y., Loy, C.T.: Analysis of rotating laminated cylindrical shells by different thin shell theories. J. Sound Vib. 186(1), 23–35 (1995)
Lam, K.Y., Loy, C.T.: Influence of boundary conditions and fibre orientation on the natural frequencies of thin orthotropic laminated cylindrical shells. Compos. Struct. 31(1), 21–30 (1995)
Ip, K.H., Chan, W.K., Tse, P.C., Lai, T.C.: Vibration analysis of orthotropic thin cylindrical shells with free ends by the Rayleigh–Ritz method. J. Sound Vib. 195(1), 117–135 (1996)
Soldatos, K.P., Messina, A.: Vibration studies of cross-ply laminated shear deformable circular cylinders on the basis of orthogonal polynomials. J. Sound Vib. 218(2), 219–243 (1998)
Messina, A., Soldatos, K.P.: Ritz-type dynamic analysis of cross-ply laminated circular cylinders subjected to different boundary conditions. J. Sound Vib. 227(4), 749–768 (1999)
Zhang, X.M.: Vibration analysis of cross-ply laminated composite cylindrical shells using the wave propagation approach. Appl. Acoust. 62(11), 1221–1228 (2001)
Zhang, X.M.: Parametric analysis of frequency of rotating laminated composite cylindrical shells with the wave propagation approach. Comput. Methods Appl. Mech. Eng. 191(19), 2057–2071 (2002)
Shao, Z.S., Ma, G.W.: Free vibration analysis of laminated cylindrical shells by using Fourier series expansion method. J. Thermoplast. Compos. Mater. 20(6), 551–573 (2007)
Jin, G., Ye, T., Chen, Y., Su, Z., Yan, Y.: An exact solution for the free vibration analysis of laminated composite cylindrical shells with general elastic boundary conditions. Compos. Struct. 106(12), 114–127 (2013)
Ye, T., Jin, G., Su, Z., Jia, X.: A unified Chebyshev–Ritz formulation for vibration analysis of composite laminated deep open shells with arbitrary boundary conditions. Arch. Appl. Mech. 84(4), 441–471 (2014)
Song, X., Han, Q., Zhai, J.: Vibration analyses of symmetrically laminated composite cylindrical shells with arbitrary boundaries conditions via Rayleigh-Ritz method. Compos. Struct. 134, 820–830 (2015)
Song, X., Zhai, J., Chen, Y., Han, Q.: Traveling wave analysis of rotating cross-ply laminated cylindrical shells with arbitrary boundaries conditions via Rayleigh–Ritz method. Compos. Struct. 133, 1101–1115 (2015)
Sun, W., Zhu, M., Wang, Z.: Free vibration analysis of a hard-coating cantilever cylindrical shell with elastic constraints. Aerosp. Sci. Technol. 63, 232–244 (2017)
Qin, Z., Chu, F., Jean, Z.U.: Free vibrations of cylindrical shells with arbitrary boundary conditions: a comparison study. Int. J. Mech. Sci. 133, 91–99 (2017)
Chen, Y., Jin, G., Liu, Z.: Free vibration analysis of circular cylindrical shell with non-uniform elastic boundary constraints. Int. J. Mech. Sci. 74(3), 120–132 (2013)
Xie, K., Chen, M., Zhang, L., Xie, D.: Free and forced vibration analysis of non-uniformly supported cylindrical shells through wave based method. Int. J. Mech. Sci. 128, 512–526 (2017)
Ganapathi, M., Varadan, T.K.: Nonlinear free flexural vibrations of laminated circular cylindrical shells. Compos. Struct. 30(1), 33–49 (1995)
Jansen, E.L.: The effect of static loading and imperfections on the nonlinear vibrations of laminated cylindrical shells. J. Sound Vib. 315(4–5), 1035–1046 (2008)
Qu, Y., Long, X., Wu, S., Meng, G.: A unified formulation for vibration analysis of composite laminated shells of revolution including shear deformation and rotary inertia. Compos. Struct. 98(3), 169–191 (2013)
Qu, Y., Hua, H., Meng, G.: A domain decomposition approach for vibration analysis of isotropic and composite cylindrical shells with arbitrary boundaries. Compos. Struct. 95, 307–321 (2013)
Wang, Y.Q., Liang, L., Guo, X.H.: Internal resonance of axially moving laminated circular cylindrical shells. J. Sound Vib. 332(24), 6434–6450 (2013)
Yan, Q.W.: Nonlinear vibration of a rotating laminated composite circular cylindrical shell: traveling wave vibration. Nonlinear Dyn. 77(4), 1693–1707 (2014)
Dey, T., Ramachandra, L.S.: Non-linear vibration analysis of laminated composite circular cylindrical shells. Compos. Struct. 163, 89–100 (2017)
Tang, Q., Li, C., Wen, B.: Analysis on forced vibration of thin-wall cylindrical shell with nonlinear boundary condition. Shock Vib. 2016(2016-2-18), 1–22 (2016)
Tang, Q., Li, C., She, H., Wen, B.: Modeling and dynamic analysis of bolted joined cylindrical shell. Nonlinear Dynamics(5), 1–23 (2018)
Bich, D.H., Nguyen, N.X.: Nonlinear vibration of functionally graded circular cylindrical shells based on improved Donnell equations. J. Sound Vib. 331(25), 5488–5501 (2012)
Amabili, M., Pellicano, F., Paidoussis, M.: Nonlinear vibrations of simply supported, circular cylindrical shells, coupled to quiescent fluid. J. Fluids Struct. 12(7), 883–918 (1998)
Pellicano, F., Amabili, M., PaïDoussis, M.P.: Effect of the geometry on the non-linear vibration of circular cylindrical shells. Int. J. Non-linear Mech. 37(7), 1181–1198 (2002)
Reddy, J.N., Chandrashekhara, K.: Geometrically non-linear transient analysis of laminated, doubly curved shells. Int. J. Non-linear Mech. 20(2), 79–90 (1985)
Acknowledgements
The Project is supported by the China Natural Science Funds (No. 51575093) and the Fundamental Research Funds for the Central Universities (Nos. N160313001 and N170308028).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that there is no conflict of interests regarding the publication of this article.
Appendices
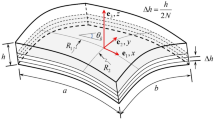
Appendix A: The strains of mid-surface and curvature
Appendix B: The stretching, coupling and bending stiffness coefficients
where p is the pth layer of the shell. In addition, all the \(B_{ij}\) terms become zero for cylindrical shells laminated symmetrically with respect to their middle surfaces.
Appendix C: The mode vector U, V, and W
\(T_m^*\left( \xi \right) \) is a Chebyshev polynomial of displacement components, \(T_m^*\left( \xi \right) =T_m \left( {2\xi -1} \right) ,T_m \left( \xi \right) \) is the Chebyshev polynomials of the first kind, of which the recurrence expressions are given by
In the process of constructing Chebyshev polynomials, the polynomials are defined in the interval \([-\,1, 1]\), while \(\xi \in \left[ {0, 1} \right] \), and the transformation of coordinates from \(\xi \) to \(2\xi -1\) is necessary.
Appendix D: Expressions for the mass matrix
The mass matrix Min Eq. (17) is expressed as
where
Appendix E: Expressions of the stiffness matrix
The stiffness matrix Kin Eq. (17) is expressed as
where
Appendix F: Expressions of the nonlinear section
- (1)
Nonlinear section \(\hbox {U}_{{\varvec{Q}}}\) of laminated composite thin cylindrical shells
$$\begin{aligned} {U_Q}= \frac{L}{R}\int _0^1 {\int _0^{2\pi } {\left\{ {\left. \begin{array}{l} \frac{{{A_{11}}{R^2}}}{{2{L^3}}}{{\varvec{q}}_{\varvec{w}}}^\mathrm{T}\frac{{\partial \bar{{\varvec{W}}}}}{{\partial \xi }}\frac{{\partial {{\bar{{\varvec{W}}}}^\mathrm{T}}}}{{\partial \xi }}{{\varvec{q}}_{\varvec{w}}}\frac{{\partial {{\bar{{\varvec{U}}}}^\mathrm{T}}}}{{\partial \xi }}{{\varvec{q}}_{\varvec{u}}}\\ + \frac{{{A_{12}}}}{{2L}}{{\varvec{q}}_{\varvec{w}}}^\mathrm{T}\frac{{\partial \bar{{\varvec{W}}}}}{{\partial \theta }}\frac{{\partial {{\bar{{\varvec{W}}}}^\mathrm{T}}}}{{\partial \theta }}{{\varvec{q}}_{\varvec{w}}}\frac{{\partial {U^T}}}{{\partial \theta }}{{\varvec{q}}_{\varvec{u}}}\\ +\frac{{2{A_{66}}}}{L}{{\varvec{q}}_{\varvec{u}}}^\mathrm{T}\frac{{\partial \bar{{\varvec{U}}}}}{{\partial \theta }}\frac{{\partial {{\bar{{\varvec{W}}}}^\mathrm{T}}}}{{\partial \xi }}{{\varvec{q}}_{\varvec{w}}}\frac{{\partial {{\bar{{\varvec{W}}}}^\mathrm{T}}}}{{\partial \theta }}{{\varvec{q}}_{\varvec{w}}}\\ + \frac{{{A_{12}}}}{{2L}}{{\varvec{q}}_{\varvec{u}}}^\mathrm{T}\frac{{\partial \bar{{\varvec{U}}}}}{{\partial \xi }}\frac{{\partial {{\bar{\mathrm{W}}}^\mathrm{T}}}}{{\partial \theta }}{{\varvec{q}}_{\varvec{w}}}\frac{{\partial {{\bar{{\varvec{W}}}}^\mathrm{T}}}}{{\partial \theta }}{{\varvec{q}}_{\varvec{w}}}\\ + \frac{{{A_{11}}{R^2}}}{{2{L^3}}}{{\varvec{q}}_{\varvec{u}}}^\mathrm{T}\frac{{\partial \bar{{\varvec{U}}}}}{{\partial \xi }}\frac{{\partial {{\bar{{\varvec{W}}}}^\mathrm{T}}}}{{\partial \xi }}{{\varvec{q}}_{\varvec{w}}}\frac{{\partial {{\bar{{\varvec{W}}}}^\mathrm{T}}}}{{\partial \xi }}{{\varvec{q}}_{\varvec{w}}}\\ + \frac{{2{A_{12}}R}}{{{L^2}}}{{\varvec{q}}_{\varvec{v}}}^\mathrm{T}\frac{{\partial \bar{{\varvec{V}}}}}{{\partial \theta }}\frac{{\partial {{\bar{{\varvec{W}}}}^\mathrm{T}}}}{{\partial \xi }}{{\varvec{q}}_{\varvec{w}}}\frac{{\partial {{\bar{{\varvec{W}}}}^\mathrm{T}}}}{{\partial \xi }}{{\varvec{q}}_{\varvec{w}}} \\ + \frac{{{A_{12}}R}}{{{L^2}}}{{\varvec{q}}_{\varvec{w}}}^\mathrm{T}\frac{{\partial \bar{{\varvec{W}}}}}{{\partial \xi }}\frac{{\partial {{\bar{{\varvec{W}}}}^\mathrm{T}}}}{{\partial \xi }}{{\varvec{q}}_{\varvec{w}}}\frac{{\partial {{\bar{{\varvec{V}}}}^\mathrm{T}}}}{{\partial \theta }}{{\varvec{q}}_{\varvec{v}}}\\ + \frac{{{A_{22}}}}{{2R}}{{\varvec{q}}_{\varvec{v}}}^\mathrm{T}\frac{{\partial \bar{{\varvec{V}}}}}{{\partial \theta }}\frac{{\partial {{\bar{{\varvec{W}}}}^\mathrm{T}}}}{{\partial \theta }}{{\varvec{q}}_{\varvec{w}}}\frac{{\partial {{\bar{{\varvec{W}}}}^\mathrm{T}}}}{{\partial \theta }}{{\varvec{q}}_{\varvec{w}}} \\ + \frac{{2{A_{66}}R}}{{{L^2}}}{{\varvec{q}}_{\varvec{v}}}^\mathrm{T}\frac{{\partial \bar{{\varvec{V}}}}}{{\partial \xi }}\frac{{\partial {{\bar{{\varvec{W}}}}^\mathrm{T}}}}{{\partial \xi }}{{\varvec{q}}_{\varvec{w}}}\frac{{\partial {{\bar{\varvec{W}}}^\mathrm{T}}}}{{\partial \theta }}{{\varvec{q}}_{\varvec{w}}}\\ + \frac{{{A_{22}}}}{R}{{\varvec{q}}_{\varvec{w}}}^\mathrm{T}\frac{{\partial \bar{\varvec{W}}}}{{\partial \theta }}\frac{{\partial {{\bar{\varvec{W}}}^\mathrm{T}}}}{{\partial \theta }}{{\varvec{q}}_{\varvec{w}}}\frac{{\partial {{\bar{\varvec{V}}}^\mathrm{T}}}}{{\partial \theta }}{{\varvec{q}}_{\varvec{v}}}\\ + \frac{{{A_{12}}R}}{{2{L^2}}}{{\varvec{q}}_{\varvec{w}}}^\mathrm{T}\bar{\varvec{W}}\frac{{\partial {{\bar{\varvec{W}}}^\mathrm{T}}}}{{\partial \xi }}{{\varvec{q}}_{\varvec{w}}}\frac{{\partial {{\bar{\varvec{W}}}^\mathrm{T}}}}{{\partial \xi }}{{\varvec{q}}_{\varvec{w}}}\\ + \frac{{{A_{22}}}}{{2R}}{{\varvec{q}}_{\varvec{w}}}^\mathrm{T}\bar{\varvec{W}}\frac{{\partial {{\bar{\varvec{W}}}^\mathrm{T}}}}{{\partial \theta }}{{\varvec{q}}_{\varvec{w}}}\frac{{\partial {{\bar{\varvec{W}}}^\mathrm{T}}}}{{\partial \theta }}{{\varvec{q}}_{\varvec{w}}}\\ + \frac{{{A_{12}}R}}{{2{L^2}}}{{\varvec{q}}_{\varvec{w}}}^\mathrm{T}\frac{{\partial {\varvec{W}}}}{{\partial \xi }}\frac{{\partial {{\bar{W}}^T}}}{{\partial \xi }}{q_w}{{\bar{W}}^T}{q_w}\\ + \frac{{{A_{22}}}}{{2R}}{q_w}^T\frac{{\partial \bar{W}}}{{\partial \theta }}\frac{{\partial {{\bar{W}}^T}}}{{\partial \theta }}{q_w}{{\bar{W}}^T}{q_w}\\ \frac{{{A_{11}}{R^2}}}{{4{L^4}}}{{\varvec{q}}_{\varvec{w}}}^\mathrm{T}\frac{{\partial \bar{\varvec{W}}}}{{\partial \xi }}\frac{{\partial {{\bar{\varvec{W}}}^\mathrm{T}}}}{{\partial \xi }}{{\varvec{q}}_{\varvec{w}}}{{\varvec{q}}_{\varvec{w}}}^\mathrm{T}\frac{{\partial \bar{\varvec{W}}}}{{\partial \xi }}\frac{{\partial {{\bar{\varvec{W}}}^\mathrm{T}}}}{{\partial \xi }}{{\varvec{q}}_{\varvec{w}}}\\ + \frac{{{A_{22}}}}{{4{R^2}}}{{\varvec{q}}_{\varvec{w}}}^\mathrm{T}\frac{{\partial \bar{\varvec{W}}}}{{\partial \theta }}\frac{{\partial {{\bar{\varvec{W}}}^\mathrm{T}}}}{{\partial \theta }}{{\varvec{q}}_{\varvec{w}}}{{\varvec{q}}_{\varvec{w}}}^\mathrm{T}\frac{{\partial \bar{\varvec{W}}}}{{\partial \theta }}\frac{{\partial {{\bar{\varvec{W}}}^\mathrm{T}}}}{{\partial \theta }}{{\varvec{q}}_{\varvec{w}}}\\ + \frac{{{A_{12}}}}{{4{L^2}}}{{\varvec{q}}_{\varvec{w}}}^\mathrm{T}\frac{{\partial \bar{\varvec{W}}}}{{\partial \theta }}\frac{{\partial {{\bar{\varvec{W}}}^T}}}{{\partial \theta }}{{\varvec{q}}_{\varvec{w}}}{{\varvec{q}}_{\varvec{w}}}^\mathrm{T}\frac{{\partial \bar{\varvec{W}}}}{{\partial \xi }}\frac{{\partial {{\bar{\varvec{W}}}^\mathrm{T}}}}{{\partial \xi }}{{\varvec{q}}_{\varvec{w}}}\\ + \frac{{{A_{12}}}}{{4{L^2}}}{{\varvec{q}}_{\varvec{w}}}^\mathrm{T}\frac{{\partial \bar{\varvec{W}}}}{{\partial \xi }}\frac{{\partial {{\bar{\varvec{W}}}^\mathrm{T}}}}{{\partial \xi }}{{\varvec{q}}_{\varvec{w}}}{{\varvec{q}}_{\varvec{w}}}^\mathrm{T}\frac{{\partial \bar{\varvec{W}}}}{{\partial \theta }}\frac{{\partial {{\bar{\varvec{W}}}^\mathrm{T}}}}{{\partial \theta }}{{\varvec{q}}_{\varvec{w}}}\\ + \frac{{{A_{66}}}}{{{L^2}}}{{\varvec{q}}_{\varvec{w}}}^\mathrm{T}\frac{{\partial \bar{\varvec{W}}}}{{\partial \xi }}\frac{{\partial {{\bar{\varvec{W}}}^\mathrm{T}}}}{{\partial \theta }}{{\varvec{q}}_{\varvec{w}}}{{\varvec{q}}_{\varvec{w}}}^\mathrm{T}\frac{{\partial \bar{\varvec{W}}}}{{\partial \xi }}\frac{{\partial {{\bar{\varvec{W}}}^\mathrm{T}}}}{{\partial \theta }}{{\varvec{q}}_{\varvec{w}}} \end{array} \right\} } \right. \mathrm{{d}}\theta \mathrm{{d}}\xi } } \nonumber \\ \end{aligned}$$(F.1) - (2)
Element of nonlinear vector \({\varvec{Q}}'\)
The nonlinear vector \({\varvec{Q}}'\) in Eqs. (17) is expressed as
where
Appendix G: Expressions of the spring stiffness matrix
The nonlinear vector \({{\varvec{Q}}}'\) in Eqs. (17) is expressed as
- (a)
The spring stiffness matrix \({\varvec{K}}_\mathrm{spr}\) of the arcs-supported boundary condition
$$\begin{aligned} K_{\mathrm{spr}}^{uu}= & {} \sum \limits _{\mathrm{{s}} = 1}^{\mathrm{NS}} {\int _{{\theta _s}}^{\theta {'_s}} {\left( {k_{u,s}^0{\bar{{\varvec{U}}}}\left( 0 \right) {{{\bar{{\varvec{U}}}}}^\mathrm{T}}\left( 0 \right) + k_{u,s}^1{\bar{{\varvec{U}}}}\left( 1 \right) {{{\bar{{\varvec{U}}}}}^\mathrm{T}}\left( 1 \right) } \right) R} \mathrm{{d}}\theta } \nonumber \\ \end{aligned}$$(G.2)$$\begin{aligned} K_{\mathrm{spr}}^{vv}= & {} \sum \limits _{s = 1}^{\mathrm{NS}} {\int _{{\theta _s}}^{\theta {'_s}} {\left( {k_{v,s}^0{\bar{{\varvec{V}}}}\left( 0 \right) {{{\bar{{\varvec{V}}}}}^\mathrm{T}}\left( 0 \right) + k_{v,s}^1{\bar{{\varvec{V}}}}\left( 1 \right) {{{\bar{{\varvec{V}}}}}^\mathrm{T}}\left( 1 \right) } \right) R} \mathrm{{d}}\theta } \nonumber \\ \end{aligned}$$(G.3)$$\begin{aligned} K_{\mathrm{spr}}^{ww}= & {} \sum \limits _{\mathrm{s} = 1}^{\mathrm{NS}} {\int _{{\theta _s}}^{\theta {'_s}} {\left( {k_{w,s}^0{\bar{{\varvec{W}}}}\left( 0 \right) {{{\bar{{\varvec{W}}}}}^\mathrm{T}}\left( 0 \right) + \frac{{k_{\theta ,s}^0}}{{{L^2}}}\frac{{\partial {\bar{{\varvec{W}}}}\left( 0 \right) }}{{\partial \xi }}\frac{{\partial {{{\bar{{\varvec{W}}}}}^\mathrm{T}}\left( 0 \right) }}{{\partial \xi }}} \right. } } \nonumber \\&+\,k_{w,s}^1{\bar{{\varvec{W}}}}\left( 1 \right) {{{\bar{{\varvec{W}}}}}^\mathrm{T}}\left( 1 \right) \nonumber \\&\left. { +\,\frac{{k_{\theta ,s}^1}}{{{L^2}}}\frac{{\partial {\bar{{\varvec{W}}}}\left( 1 \right) }}{{\partial \xi }}\frac{{\partial {\bar{{\varvec{W}}}}{{\left( 1 \right) }^\mathrm{T}}}}{{\partial \xi }}} \right) R\mathrm{{d}}\theta \end{aligned}$$(G.4) - (b)
The spring stiffness matrix \({\varvec{K}}_\mathrm{spr}\) of the points-supported boundary condition
$$\begin{aligned} {K_{\mathrm{spr}}^{uu}}= & {} \sum \limits _{p = 1}^{\mathrm{NA}} \left( {k'^{o}_{\mathrm{u},p}}{\bar{{\varvec{U}}}}\left( {0,{\theta _{p}}} \right) {{{\bar{{\varvec{U}}}}}^\mathrm{T}}\left( {0,{\theta _{p}}} \right) \right. \nonumber \\&\left. +\,{k'^{1}_{u,p}}{\bar{{\varvec{U}}}}\left( {0,{\theta _{p}}} \right) {{{\bar{{\varvec{U}}}}}^\mathrm{T}}\left( {0,{\theta _{p}}} \right) \right) \end{aligned}$$(G.5)$$\begin{aligned} {K^{vv}_\mathrm{spr}}= & {} \sum \limits _{p = 1}^{\mathrm{NA}} \left( {k'^{0}_{v,p}}{\bar{{\varvec{V}}}}\left( {0,{\theta _p}} \right) {{{\bar{V}}}^\mathrm{T}}\left( {0,{\theta _p}} \right) \right. \nonumber \\&\left. +\, {k'^{1}_{v,p}}{\bar{{\varvec{V}}}}\left( {1,{\theta _p}} \right) {{{\bar{{\varvec{V}}}}}^\mathrm{T}}\left( {1,{\theta _p}} \right) \right) \end{aligned}$$(G.6)$$\begin{aligned} {K^{ww}_\mathrm{spr}}= & {} \sum \limits _{p = 1}^{\mathrm{NA}} \left( {k'^{0}_{w,p}}{\bar{{\varvec{W}}}}\left( {0,{\theta _p}} \right) {{{\bar{{\varvec{W}}}}}^\mathrm{T}}\left( {0,{\theta _p}} \right) \right. \nonumber \\&\left. +\, \frac{{{k'^{0}_{\theta ,s}}}}{{{L^2}}}\frac{{\partial {\bar{{\varvec{W}}}}\left( {0,{\theta _p}} \right) }}{{\partial \xi }}\frac{{\partial {\bar{{\varvec{W}}}}{{\left( {0,{\theta _p}} \right) }^\mathrm{T}}}}{{\partial \xi }} \right. \nonumber \\&+\,{k}_{w,p}^{\prime 1}{\bar{{\varvec{W}}}}\left( {1,{\theta _p}} \right) {{{\bar{{\varvec{W}}}}}^\mathrm{T}}\left( {1,{\theta _p}} \right) \nonumber \\&\left. +\,\frac{{{k^\prime {1}_{\theta ,p}}}}{{{L^2}}}\frac{{\partial {\bar{{\varvec{W}}}}\left( {1,{\theta _p}} \right) }}{{\partial \xi }}\frac{{\partial {\bar{{\varvec{W}}}}{{\left( {1,{\theta _p}} \right) }^\mathrm{T}}}}{{\partial \xi }} \right) \nonumber \\ \end{aligned}$$(G.7)
Appendix H: Expressions of the damping matrix
Rayleigh damping C is considered during analysis of the vibration response of laminated cylindrical shells, and it is given as follows
where\(\alpha , \beta \) are the damping parameters
where \(\omega _1, \omega _2\) are the first-order and second-order natural frequencies of laminated cylindrical shell, and \(\xi _1,\xi _2\) are the damp coefficient.
Rights and permissions
About this article
Cite this article
Li, C., Li, P., Zhong, B. et al. Geometrically nonlinear vibration of laminated composite cylindrical thin shells with non-continuous elastic boundary conditions. Nonlinear Dyn 95, 1903–1921 (2019). https://doi.org/10.1007/s11071-018-4667-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-018-4667-2