Sparse Versus Simple Structure Loadings

Abstract

The component loadings are interpreted by considering their magnitudes, which indicates how strongly each of the original variables relates to the corresponding principal component. The usual ad hoc practice in the interpretation process is to ignore the variables with small absolute loadings or set to zero loadings smaller than some threshold value. This, in fact, makes the component loadings sparse in an artificial and a subjective way. We propose a new alternative approach, which produces sparse loadings in an optimal way. The introduced approach is illustrated on two well-known data sets and compared to the existing rotation methods.

1 Introduction

The goal of the simple structure approach is to transform some initial component loadings matrix into a new one having simple structure, and thus is easier to interpret. The adopted transformations are orthogonal or oblique rotations, which give the name rotation methods. Originally, the simple structure concept was introduced in factor analysis (FA) as three rules in the 30s of the last century, and was later extended and elaborated (Thurstone, 1947, p. 335). In formal terms, the simple structure approach finds a rotation, which optimizes certain objective function defining the Thurstone’s simple structure concept as a single formula. Later, the simple structure approach was adapted to principal component analysis (PCA) to make the rotated component loadings as interpretable as possible (Jolliffe, 2002, Chap. 11).

We stress on the fact that the original simple structure concept requires vanishing and, in fact, sparse loadings. The term ‘sparse loadings’ was introduced by Zou, Hastie, and Tibshirani (2006) and means a matrix of component loadings containing a lot of zero entries. Unfortunately, true sparseness has never been achieved by the classical rotation methods.

We propose a new alternative approach, which produces sparse loadings in an optimal way. The introduced approach is illustrated on two well-known data sets and compared to the existing rotation methods.

2 Rotated Component Loadings

The rotation methods have a long history. Browne (2001) gives a comprehensive overview of the field. Some additional aspects are discussed (Jennrich, 2007). Details can be found in the papers cited there and in the standard texts on FA (Harman, 1976; Mulaik, 2010; Thurstone, 1947).

Let $X$ be a given $n \times p (n > p)$ data matrix. To simplify the further notations, $X$ is assumed to be standardized and divided by $\sqrt{n-1}$. Then, the sample correlation matrix of the original data is simply given by $X^\top X$. Let the economy singular value decomposition (SVD) of $X$ be given as $X = F D A^\top$, where $F$ is $n \times p$ orthonormal, $A$ is $p \times p$ orthogonal and $D$ is $p \times p$ diagonal, whose elements are called singular values of $X$ and are in decreasing order. For any $r(< p)$, let $X_r = F_r D_r A_r^\top$ be the truncated SVD of $X$, where $F_r$ and $A_r$ denote the first $r$ columns of $F$ and $A$, respectively ($F_r^\top F_r = A_r^\top A_r = I_r$), and $D_r$ is diagonal matrix with the first largest $r$ singular values of $X$. It is well known that $X_r$ gives the best least-squares (LS) approximation of rank $r$ to $X$, i.e. $X \approx X_r = F_r D_r A_r^\top$. The PCA of $X$ is based on such truncated SVD and $r$ is usually taken as considerably smaller than $p$, i.e. $r \ll p$. From now on $F\equiv F_r, A\equiv A_r$ and $D\equiv D_r$.

After the invention of the rotation methods in context of FA, they were later employed in PCA as well. The utilization of the rotation methods in PCA is based on the following simple identity:

$$\begin{aligned} X \approx F D A^\top = F Q Q^{-1} D A^\top = F Q (A D Q^{-\top })^\top \ , \end{aligned}$$

(1)

which represents PCA as introduced by Hotelling (1933). Here, $F$ is the $n \times r$ matrix of component scores and $L = AD$ is the $p \times r$ matrix of component loadings. The number $r$ of principal components is fixed in advance and $Q$ is any $r \times r$ non-singular transformation matrix. Two types of matrices $Q$ are used in PCA: orthogonal and oblique. The sets of orthogonal and oblique matrices are denoted, respectively, by ${\mathcal {O}}(r)$ and ${\mathcal {OB}}(r)$ and form smooth matrix manifolds (Absil, Mahony, & Sepulchre 2008). We remind that a non-singular matrix $Q$ is called oblique if $Q^\top Q$ is a correlation matrix. We also denote the set of all $p \times r$ orthonormal matrices known as the Steiefel manifold by ${\mathcal {O}}(p,r)$.

The simple structure rotation approach proceeds as follows. First, the dimension reduction is performed, i.e. the appropriate $r$ is chosen, and $A$ and $D$ are obtained. Then, a rotation $Q$ is found by optimizing certain simple structure criterion, such that the resulting $LQ^{-\top }$ has a simple structure.

Thurstone (1947) introduced a category of methods known as hyperplane counting methods. As suggested by their name, they count the variables, close to certain hyperplane, and then try to maximize their number. Recently the rationale behind these methods inspired the introduction of a class of rotation criteria called component loss functions (CLF) (Jennrich, 2004, 2006). The most intriguing of them is given by the $\ell _1$ matrix norm of the rotated loadings, defined for any $p \times r$ matrix $A$ as $\Vert A\Vert _{\ell _1} = \sum _i^p \sum _j^r |a_{ij}|$. The reason for referring to the CLF method here is twofold: first, it seems to be working well on a number of test data (Mulaik, 2010, p. 360–366); and second, its definition involves $\ell _1$ norm, which is probably influenced by and corresponds to the recent considerable interest in sparse PCA (Jolliffe, Trendafilov, & Uddin 2003; Zou et al., 2006). The CLF method is defined for orthogonal rotations $Q$ as (Jennrich, 2004)

$$\begin{aligned} \min _{Q \in {\mathcal {O}}(r)} \Vert L Q\Vert _{\ell _1} \ , \end{aligned}$$

(2)

where $L = AD$ is the matrix of component loadings introduced above. The orthogonal CLF simple structure rotation (2) does not always produce satisfying results. For this reason, the oblique CLF is usually applied instead (Jennrich, 2006). It is defined as

$$\begin{aligned} \min _{Q \in {\mathcal {OB}}(r)} \Vert L Q^{-\top }\Vert _{\ell _1} \ . \end{aligned}$$

(3)

3 Alternative Simple Structure Rotation

One can notice that instead of using (1), the PCA interpretation can be based on the following alternative identity:

$$\begin{aligned} X \approx F D A^\top = F D Q Q^{-1} A^\top = F D Q (A Q^{-\top })^\top \ , \end{aligned}$$

(4)

where the matrix of component loadings is taken to be $L = A$. Obviously, one can consider infinite number of other equivalent representations, and (1) and (4) are simply the most popular of them. This lack of uniqueness is known as the normalization problem in PCA (Jolliffe, 2002, p. 272–275).

To compare this PCA definition with the Hotelling’s one, let $P$ and $L$ denote principal components and loadings. Then, in the Hotelling case $P = F$ and $L = AD$, and in case of (4) one has $P = FD$ and $L = A$. Thus, the Hotelling’s definition of PCA (1) gives uncorrelated principal components ($P^\top P = F^\top F = I_r$) and component loadings $L = AD$ with orthogonal columns ($L^\top L = DA^\top AD = D^2$). The alternative PCA definition (4) also gives uncorrelated principal components ($P^\top P = DF^\top FD = D^2$) and, in addition, orthonormal component loadings $L = A$ ($L^\top L = A^\top A = I_r$). For this reason, the latter definition is preferred and adopted in modern PCA.

The rotated component loadings $L Q^{-\top }$ are interpreted. The classic approach to rotate $L = AD$ destroys the order of the components according to their decreasing variance. Moreover, these rotated loadings are not orthonormal even for orthogonal rotation $Q$, which complicates their interpretation both within and between the components. Indeed, let $B = L Q^{-\top } = A D Q^{-\top }$ be the classic rotated loadings. Then $B^\top B = Q^{-1} D A^\top A D Q^{-\top } = Q^{-1} D^2 Q^{-\top }$, which cannot be identity matrix $I_r$ for any orthogonal or oblique $Q$.

Following the notations from (1), one can calculate the variance of the classic rotated principal components $F Q = X A D^{-1} Q$ as

$$\begin{aligned} \text{ var }(F Q) = Q^\top \text{ var }(F) Q = Q^\top D^{-1} A^\top \text{ var }(X)A D^{-1} Q = Q^\top Q \ . \end{aligned}$$

(5)

It follows from (5) that for classic orthogonal rotation $Q$ the rotated principal components remain uncorrelated, which is the main benefit from such type of rotation. For oblique $Q$, the rotated principal components are correlated and their correlation (and covariance) matrix is given by $Q^\top Q$.

In contrast to the classic rotation methods, the rotation of $L = A$ as in (4) gives orthonormal rotated loadings after an orthogonal rotation $Q$. Indeed, the alternative rotated loadings are $B = A Q^{-\top }$, and thus $B^\top B = Q^{-1} A^\top A Q^{-\top } = Q^{-1} Q^{-\top } = (Q^\top Q)^{-1}$. The orthonormal loadings are easier to interpret both within and between the components. The variance of the rotated alternative principal components $F D Q = X A Q$ is found to be

$$\begin{aligned} \text{ var }(F D Q) = \text{ var }(X A Q) = Q^\top D A^\top \text{ var }(X)A D Q = Q^\top D^2 Q \ , \end{aligned}$$

(6)

which clearly shows that the alternative rotated principal components are always correlated, even for orthogonal rotation $Q$. For orthogonal $Q$, one also has that $\text{ trace }(Q^\top D^2 Q) = \text{ trace }(D^2)$, i.e. the total variance of the rotated components is equal to the total variance of the principal components. We remind that total variance of an $n \times m$ matrix $Y$ is the sum of the variances of its columns. Note that if the columns of $Y$ have mean zero, $n$ times the total variance equals $\Vert Y \Vert ^2$.

The application of standard rotation methods on component loadings $L = A$ on two well-known data sets is illustrated in Section 5. As it can be expected, the interpretation of the rotated loadings $L Q^{-\top }$ is very much the same for $L = A$ and $L =AD$, as they are proportional. However, the features of the component loadings and the corresponding principal components differ.

4 True Simple Structure: Sparse Loadings

4.1 The Rationale

The original simple structure concept was introduced in FA as three rules (Thurstone, 1935, p. 156), which was later extended and elaborated (Thurstone, 1947, p. 335). In more contemporary language they look as follows (Harman, 1976, p. 98), where the term ‘factor matrix’ used in FA context should be understood as component loadings matrix for the PCA case:

• 1. Each row of the factor matrix should have at least one zero,

• 2. If there are $r$ common factors, each column of the factor matrix should have at least $r$ zeros,

• 3. For every pair of columns of the factor matrix there should be several variables whose entries vanish in one column but not in the other,

• 4. For every pair of columns of the factor matrix, a large proportion of the variables should have vanishing entries in both columns when there are four or more factors,

• 5. For every pair of columns of the factor matrix there should be only a small number of variables with non-vanishing entries in both columns.

The words in italic are made by us to stress that the original simple structure concept requires, in fact, sparse loadings. Unfortunately, this sparseness has never been achieved by the classical rotation methods.

There are situations when the first principal component is a measure of ‘overall size’ with non-trivial loadings for all variables. The same phenomenon occurs in the so-called Bi-factor analysis (Harman, 1976, pp. 120–127). In such situations, the five rules are applied to the remaining PCs/factors.

The main weakness of the rotation methods is that they produce plenty of small non-zero loadings, part of which should be neglected subjectively. This problem is unavoidable with the rotation methods as they facilitate the interpretation while preserving the variance explained by the initial dimension reduction. The variance explained by the first $r$ principal components is simply the total variance of $FDA^\top$. Then, for both (1) and (4) one finds that $\text{ var }(F Q Q^{-1} D A^\top ) = \text{ var }(F D Q Q^{-1} A^\top ) = \text{ var }(F D A^\top ) = \text{ trace } D^2$.

The common practice to interpret the (rotated) component loadings is to set all the loadings with magnitudes less than some threshold to zero. However, working with truncated loadings means working with sparse loadings which are found in a loose and subjective way. The rotation methods never tried to relate the thresholding process with the optimal features of the principal components when their loadings are replaced by truncated ones. Cadima and Jolliffe (1995) summarize this situation as follows: ‘Thresholding requires a degree of arbitrariness and affects the optimality and uncorrelatedness of the solutions with unforeseeable consequences’. They also show that discarding small component loadings can be misleading, especially when working with covariance matrices.

In the last decade, it became clear that there are situations (e.g. analysing large data) when it would be desirable to put more emphasis on the interpretation simplicity than on variance maximization. The attempts to achieve this goal led to the modern sparse PCA subject to additional LASSO or other sparseness-inducing constraints (Trendafilov, 2013). It turns out that many of the original variables are redundant and sparse solutions, and involving only small proportion of them can do the job reasonably well.

4.2 SPARSIMAX: Rotation-Like Sparse Loadings

Assume that the dimension reduction is already performed and the appropriate number $r$ of PCs to retain is chosen, and the corresponding $A$ and $D$ are obtained. The variance explained by the first $r$ principal components and by the rotated once is $\text{ trace }(D^2)$. We want to develop a new method producing component loadings some of which are exact zeros, called sparse, which can help for their unambiguous interpretation. Components with such sparse loadings are called sparse. However, the sparse components explain less variance than $\text{ trace }(D^2)$. Thus, the new method should be designed to explain the variance as much as possible, while producing sparse loadings—which will be called rotation-like sparse loadings. The new method is named SPARSIMAX to keep up with the tradition of the simple structure rotation methods.

For this reason, consider first the following problem:

$$\begin{aligned} \min _{A \in {\mathcal {O}}(p,r)} [\text{ trace }(A^\top X^\top X A) - \text{ trace }(D^2)]^2\ , \end{aligned}$$

(7)

which finds an orthonormal $A$ such that the variance of $XA$ equals the variance of the first $r$ principal components of $X^\top X$. Clearly, the matrix $A$ containing the first $r$ eigenvectors of $X^\top X$ is a solution, which makes the objective function (7) zero. Note that this solution is not unique.

After having a way to find loadings $A$ that explain the variance $\text{ trace }(D^2)$, let us take care for their interpretability. We can follow the idea already employed by the CLF methods and require that the $\ell _1$ matrix norm of $A$ is minimized. This can be readily arranged by introducing the term $\Vert A \Vert _{\ell _1}$ in (7), which results in the following optimization problem:

$$\begin{aligned} \min _{A \in {\mathcal {O}}(p,r)} \Vert A \Vert _{\ell _1} + \tau [\text{ trace }(A^\top X^\top X A) - \text{ trace }(D^2)]^2\ , \end{aligned}$$

(8)

where $\tau$ is a tuning parameter controlling the sparseness of $A$. In a sense, the new method is a compromise between sparse PCA and the classic rotation methods, as it relaxes the constraint $\text{ trace }(A^\top X^\top X A) = \text{ trace }(D^2)$, but is asking in reward for sparse loadings $A$. The method is a particular case of a class of sparse PCA models introduced by Trendafilov (2013), which correspond to the Dantzig selector introduced by Candès and Tao (2007) for regression problems.

There is similarity between (8), and (2) and (3), as they aim at the minimization of the sum of the absolute values of the loadings. Another similarity is that they both produce loadings which are not ordered according to decreasing variance. However, in contrast to the CLF problems (2) and (3), the solutions $A$ of (8) only approximate the explained variance $\text{ trace }(D^2)$ by the original dimension reduction.

The solution of (8) requires minimization on the Stiefel manifold ${\mathcal {O}}(p,r)$, which is numerically a more demanding task than solving (2) and (3). For small data sets, the problem (8) can be readily solved by the projected gradient method (Jennrich, 2001), as well as the CLF problems (2) and (3). The numerical results in the paper are found by employing the dynamical system approach (Trendafilov, 2006) and an adaptation of the codes provided there. Alternatively, the codes can be obtained by the first author upon request. However, for such problems it is advisable to use optimization methods on matrix manifolds Absil et al. (2008). Relevant algorithms with much better convergence properties are freely available (?).

Table 1 Loadings obtained by solving (8) with initial loadings $A_0$, and with $\tau =0$ and $\tau =2000$.

The sparse components $XA$ are correlated for sparse loadings $A$, even for orthonormal $A$. Then, $\text{ trace }(A^\top X^\top XA)$ is not any more a suitable measure for the total variance explained by the sparse components. To take into account the correlations among the sparse components, Zou et al. (2006) proposed the following: Assuming that $XA$ has rank $r$, its QR decomposition $XA = QU$ finds a basis of $r$ orthonormal vectors collected in the orthonormal $p \times r$ matrix $Q$, such that they span the same subspace in $\mathbb {R}^p$ as $XA$. The upper triangular $r \times r$ matrix necessarily has non-zero diagonal entries. Then, the adjusted variance is defined as $\text{ AdjVar }(XA) = \text{ trace }[\text{ diag }(U)^2] \le \text{ trace }(U^\top U) = \text{ trace }(A^\top X^\top XA)$. This adjusted variance is not completely satisfying, i.e. it works only with orthonormal sparse loadings $A$. Other authors proposed alternative methods to measure the variance explained by the sparse components (Mackey, 2009; Shen & Huang 2008), which also need further improvement. In the sequel, we calculate the adjusted variance (Zou et al., 2006) of the SPARSIMAX sparse components, because the solutions of (8) are orthonormal sparse loadings $A$.

In large applications, the tuning parameter $\tau$ is usually found by cross-validation. Another popular option is employing information criteria. For small applications, as those considered in the paper, the optimal tuning parameter $\tau$ can be easily located by solving the problem for several values of $\tau$ and compromising between sparseness and fit. Another option is to solve (8) for a range of values of $\tau$ and choose the most appropriate of them based on some index of sparseness. Here we use the following one:

$$\begin{aligned} \text{ IS } = \frac{V_aV_s}{V_o^2} \times \frac{\#_0}{pr}\ , \end{aligned}$$

(9)

which is introduced in (Trendafilov, 2013). $V_a, V_s$ and $V_o$ are the adjusted, unadjusted and ordinary total variances for the problem; and $\#_0$ is the number of zeros among all $pr$ loadings of $A$. IS increases with the goodness-of-fit $(V_s/V_o)$, the higher adjusted variance $(V_a/V_o)$ and the sparseness. For equal or similar values of IS, the one with the largest adjusted variance is preferred.

4.3 Know-How for Applying SPARSIMAX

Let us illustrate how SPARSIMAX works on the small well-known data set of Five Socio-Economic Variables (Harman, 1976, Table 2.1, p. 14) containing $n = 12$ observations and $p = 5$ variables. This will also help to demonstrate the behaviour of its objective function (8).

Shortly, this data set is referred to as H5. The variance explained by the first two $(r=2)$ principal components is $2.873 + 1.797 = 4.67$, which is 93.4 % of the total variance. When $\tau =0$, the second term in (8) switches off, and the solution does not depend on $X$. Each column of the solution has only one non-zero entry equal to $\pm 1$, whose location corresponds to the one with the largest magnitude in the same column as the initial $A_0$, which was used to start the algorithm. This is illustrated in Table 1 with an initial matrix $A_0$ for solving (8) depicted in its first two columns. The SPARSIMAX solution to the H5 data with $\tau =0$ is reproduced in the middle two columns of Table 1. When $\tau$ has large enough value, the second term in (8) completely wipes out the first term. Indeed, the solution to the H5 data with $\tau =2000$ is depicted in the last two columns of Table 1. The same $A$ is obtained if one solves (7). The variances of the corresponding components are 2.4972 and 2.1726, which are 93.4 % of the total variance.

Now, let us see how SPARSIMAX is applied to the H5 data to get interpretable loadings and how they are related to the rotated loadings. The first two columns of Table 2 give the VARIMAX solution $A_V$ for the H5 data (Harman, 1976, p. 295). The next two columns give the pattern $A_P$ suggested in (Harman, 1976, p. 295) to interpret the loadings: “...In this sense the factor matrix exhibits one zero in each row, with the exception of variable 4; two zeros in each column; and several variables whose entries vanish in one column but not in the other. Even the exception of variable 4 is not contradictory to the set of simple-structure criteria (see number 5)...”.

Table 2 Simple structure and sparse loadings.

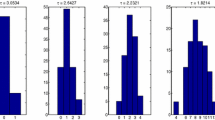
Now, we solve (8) for a range of values of $\tau$ from 1 to 100. The IS values and the adjusted variances of these solutions are plotted on the left panel of Figure 1. The IS graph on the upper plot has a ladder-like shape. Each ‘step’ corresponds to certain number of zero loadings, starting with five and going down to two zero loadings. If one needs a solution with six zero loadings, then (8) should be solved with $\tau < 1$. The solutions obtained by the tuning parameter roughly between 5 and 15 have the highest IS values. The right panel of Figure 1 depicts their values for $\tau$ from 1 to 24 (the IS value for $\tau =25$ drops to 0.1847). These are the $\tau$ values, for which the SPARSIMAX solutions have five or four zero loadings. First, we are looking for SPARSIMAX solutions with four zeros as suggested by the Harman’s simple structure pattern from Table 2. They correspond to the $\tau$ values from 16 to 24 in Figure 1 (right panel). The solution with the highest IS value (9) among all other solutions with four zeros is obtained with $\tau =19$. It is denoted as $A_{\tau =19}$ in Table 2. Its IS value is 0.3683 and its adjusted variance is 88.66 % of the total variance. Clearly, this is almost a solution with five zeros and thus, differs considerably from the Harman’s simple structure pattern. Then, we look for SPARSIMAX solutions with five zeros. They correspond to the $\tau$ values from 1 to 15 in Figure 1. The solution with the highest IS value among them is obtained with $\tau =9$. It is denoted as $A_{\tau =9}$ in Table 2. Its IS value is 0.4602 and its adjusted variance is 88.69 % of the total variance.

The conclusion is that SPARSIMAX does not find the classic simple structure $A_P$ optimal. In other words, SPARSIMAX finds the fourth loading of the second component to be redundant, while the classic approach intuitively considers it to be significantly non-zero.

Fig. 1

IS values (9) and the adjusted variances for SPARSIMAX solutions with $\tau \in [1,100]$ (left panel) and $\tau \in [1,24]$ (right panel).

5 Numerical Examples

In the sequel, the new approaches considered in Sections 3 and 4 are illustrated on two well-known data sets, which are always used when a new method for simple structure rotation is proposed. The sparse loadings obtained by SPARSIMAX will be compared with the corresponding rotated (classic) loadings using standard VARIMAX (MATLAB, 2011), and orthogonal and oblique CLF (Jennrich, 2004, 2006).

Thurstone’s 26 Box Problem: Thurstone constructed an artificial data set with 30 observations and 26 variables in the following way. He collected at random 30 boxes and measured their three dimensions $x_1$ (length), $x_2$ (width) and $x_3$ (height). The variables of the data set are twenty-six functions of these dimensions listed in Table 3. Unfortunately, these 30 boxes and their dimensions are lost, but their correlation matrix $R_{26}$ is available (Thurstone, 1947, p. 370). Its first three eigenvalues are considerably greater than the rest, and thus three components are considered. The problem is to identify the ‘latent’ three dimensions based on the component loadings. The desired simple structure is given in the first three columns of Table 3, and is defined by the zero entries. The non-zero entries are labeled by $\times$. This problem is notorious as most of the available rotation methods fail to reveal them, e.g. VARIMAX.

Next, the orthogonal CLF problem (2) is solved with $L=A$. The initial matrix $A_0$ to rotate is composed by the three eigenvectors of $R_{26}$ corresponding to the three largest eigenvalues (14.75, 5.55 and 5.01), as the rest are considerably smaller. The first three principal components explain 97.35 % of the total variance. The rotated loadings are given in the second three columns of Table 3. The correlation matrix of the rotated components is given below the loadings, and their variances are 7.81, 8.68 and 8.81. The matrix of orthogonal CLF rotation, i.e. the solution $Q$ of (2), is

$$\begin{aligned} \left( \begin{array}{c@{\quad }c@{\quad }c} .5222&{} -.5847&{} .6207\\ -.5217&{} -.7948&{} -.3099\\ -.6745&{} .1620&{} .7201\\ \end{array} \right) \ . \end{aligned}$$

Next, the same $A_0$ is rotated by oblique CLF solving (3) with $L=A$. The rotated loadings are given in the third triple of columns of Table 3. Below them is the correlation matrix of the rotation components, and their variances are 8.69, 8.37 and 7.18. The matrix of oblique CLF rotation, i.e. the solution $Q$ of (3), is

$$\begin{aligned} \left( \begin{array}{c@{\quad }c@{\quad }c} -.5850&{} -.5804&{} -.4531\\ -.7932&{} .3690&{} .5564\\ .1694&{} -.7260&{} .6965\\ \end{array} \right) \ . \end{aligned}$$

The desired simple structure is correctly identified by the CLF rotated loadings $A Q^{-\top }$. The oblique rotated CLF loadings are better in terms of fit and exact zero loadings. Hereafter, we consider any loading with magnitude less than .005 as zero. The orthogonal and oblique CLF rotations used in the examples are implemented by the first author.

Finally, the sparse orthonormal loadings obtained by solving (8) with $\tau =20$ are given in the third triple of columns of Table 3. Below them is the correlation matrix of the sparse principal components $XA$ obtained from the resulting sparse loadings $A$. Their variances are 8.69, 7.42 and 9.04. The expected simple structure is clearly and correctly identified by the 27 zero loadings. Moreover, the sparse loadings provide much clearer simple structure than the CLF solutions. The sparse components are considerably more correlated than the CLF ones, which suggests that they explain less variance than the CLF ones. Their adjusted variance is 85.82 %. One would like to truncate the orthogonal and oblique rotated CLF loadings, and find the corresponding adjusted variances. At present, this is impossible, as the truncated loadings are not orthonormal. However, one can find the adjusted variances of the components formed by the orthonormal CLF loadings, which are correlated. Their adjusted variance is 85.90 %, which is slightly more than that of the sparse components. This is rather unsatisfactory, because the orthonormal CLF loadings are dense (not sparse).

Table 3 The desired simple structure (SS) for the 26 Box data and three factor loadings matrices obtained by solving (2), (3) and (8).

Table 4 Loadings matrices for HH24 data from two algorithms.

Twenty-four psychological tests: Here, we consider the Twenty-four psychological tests for which $24 \times 24$ correlation matrix $R_{24}$ is available in (Harman, 1976, p. 124). PCA is applied to $R_{24}$. The first four principal components corresponding to the four largest eigenvalues (8.14, 2.10, 1.69 and 1.50) explain 55.96 % of the total variance and are left for further analysis. The corresponding four eigenvectors form the initial matrix $A_0$. The desired simple structure solution is widely available, (e.g. Harman, 1976, p. 296).

First, the loadings $A_0$ are rotated by standard VARIMAX, as implemented in (MATLAB, 2011), and the rotated loadings are given in the first four columns of Table 4. The correlation matrix of the rotated components is given below the loadings, and their variances are 4.02, 3.35, 3.28 and 2.78. The matrix of orthogonal VARIMAX rotation is

$$\begin{aligned} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} .5808&{} -.4804&{} .4975&{} .4293\\ .6217&{} .7038&{} .1970&{} -.2818\\ -.5252&{} .3158&{} .7718&{} .1696\\ .0177&{} .4173&{} -.3435&{} .8411\\ \end{array} \right) \ . \end{aligned}$$

Next, the orthogonal CLF problem (2) is solved with $L=A$. The same $A_0$ is rotated and the rotated loadings are given in the middle four columns of Table 4. The correlation matrix of the rotated components is given below the loadings, and their variances are 3.88, 3.43, 2.59 and 3.52. The matrix of orthogonal CLF rotation is

$$\begin{aligned} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} .5593&{} -.5202&{} -.3953&{} -.5102\\ .6536&{} -.1822&{} .2978&{} .6714\\ -.5088&{} -.7892&{} -.1038&{} .3274\\ .0307&{} .2703&{} -.8626&{} .4262\\ \end{array} \right) \ . \end{aligned}$$

The oblique CLF problem (3) is solved with $L=A$. The rotated loadings are given in the third group of four columns of Table 4, and below them is the correlation matrix of the rotated components. The variances of the rotated components are 3.54, 2.19, 4.19 and 2.99. The matrix of oblique CLF rotation is

$$\begin{aligned} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} .5120&{} -.3140&{} .6050&{} -.4509\\ -.6954&{} .2114&{} .5884&{} -.1381\\ -.2851&{} -.1272&{} -.5297&{} -.8306\\ -.4159&{} -.9169&{} .0842&{} .2964\\ \end{array} \right) \ . \end{aligned}$$

Finally, the sparse orthonormal loadings obtained by solving (8) with $\tau =5$ are given in the last four columns of Table 4 with the correlation matrix of the sparse components below them.

All the solutions identify the expected simple structure very well; however, it is most transparent with the sparse loadings. As expected, the sparse components are most correlated among these solutions, which suggests that they explain less variance than the rest. The adjusted variance of the sparse components corresponding to the depicted sparse loadings is 39.75 %. For comparison, the adjusted variance of the components corresponding to the orthonormal CLF loadings is 43.93 %.

6 Conclusion

PCA is a very popular technique for high-dimensional multivariate data analysis. The modern applications involve thousands of variables, which makes the interpretation of the component loadings a very difficult task. Jolliffe et al. (2003) modified the classic PCA to produce sparse component loadings, i.e. containing many zeros. Since then, a huge number of articles appeared for studying this important but difficult problem known now as sparse PCA (Trendafilov, 2013).

The classic psychometric applications do not share such difficulties. The typical number of psychometric variables involved is quite modest with respect to the modern computer power and other research areas, e.g. gene engineering, climate data, etc. Nevertheless, the interpretation of the component loadings is based on the discarding or neglecting of the small component loadings. In other words, the classic way of interpretation is effectively an artificial sparsification of the component loadings, which is very frequently ambiguous and subjective. Note also that the Thurstone’s simple structure concept requires ‘zero’ or ‘vanishing’ loadings.

The classic rotation methods cannot achieve exact zero loadings. Following the modern data analysis trend, we propose a reasonable alternative to the rotation methods. We obtain sparse component loadings in an objective way by compromising the amount of the total explained variance. This is the price to pay for clearer and easier interpretation. However, this is not a real weakness, because it was argued that the classic way to interpret component loadings (by discarding and/or neglecting) is, in fact, by doing the same in a rather arbitrary and most likely suboptimal way.

The proposed method SPARSIMAX is primarily intended for small- to medium-size applications. A fast algorithm for solving (8) for large data will be available shortly. The classic psychometric applications are rather small and do not really need such algorithms. However, they may be useful in case of large applications. Analysing genetic data for studying behavioural or other personality related features or disorders may well require adopting sparse methods as the one considered in the manuscript as well as relevant fast numerical algorithms. This will be a topic for future research and SPARSIMAX implementation and elaboration.

We thank the Editor, the Associate Editor and three anonymous referees for their careful and stimulating comments and suggestions on the draft versions of this paper.