1 Introduction

The Brinkman–Darcy equations have been used extensively to analyse flow of a viscous incompressible fluid in a porous medium which is not too dense in the sense that the porosity is not too small. Thermal convection in saturated porous media, which is the subject of this paper, has been intensively studied with the saturating fluid described by Brinkman–Darcy theory, see e.g. Rees [1], Postelnicu and Rees [2], Capone and Gianfrani [3], Capone et al. [4], and the references therein. The range of permeability values where the Darcy–Brinkman equations are valid is critically reviewed in Gentile and Straughan [5].

Recent research has also focussed on flow of viscoelastic fluids in porous media, where the fluid stress displays history dependent behaviour, see e.g. Amendola and Fabrizio [6], Antontsev and Rodrigues [7]. Since flow of viscoelastic fluids in porous media has immense importance practically in, for example, the oil industry, in vascular dynamics Cavallini et al. [8], we here analyse thermal convection in a model for viscoelastic flow in a porous medium by employing the Kelvin–Voigt equations in a Brinkman–Darcy porous medium.

Kelvin–Voigt fluids have been analysed in great depth from the analytical viewpoint of existence, attractors, structural stability, see e.g. Oskolkov [9], Kalantarov and Titi [10], Damazio et al. [11], and the references therein. Thermal convection in a layer of a Kelvin–Voigt fluid has been investigated recently by Straughan [12]. In addition [13, 14] has demonstrated continuous dependence of the solution for the equations of Brinkman–Darcy–Kelvin–Voigt theory for the isothermal, improperly posed, backward in time problem, and in Straughan [15] for the Kelvin–Voigt equations forward in time.

It is important to emphasize that Maxwell–Cattaneo theory for heat flow is a very rich area in modern research. In addition to heat flow, the idea behind Maxwell–Cattaneo theory where a relaxation effect is included for an appropriate flux is being employed in many diverse research areas. Such models do not generally suffer from the effect of the Fourier law of infinite speed of heat propagation, and allow heat to travel with a finite wavespeed. The technique behind Maxwell–Cattaneo theory whereby the flux equation is transformed from a constitutive equation to an evolution equation has been applied for example, in nanoscale mechanics, Sellitto et al. [16], Jou et al. [17], in sound waves in porous media, Jordan et al. [18], in temperature wave motion, Jordan and Lambers [19], Carillo and Jordan [20], Christov [21, 22], in convection in stellar atmospheres, Herrera and Falcon [23], Herrera[24], in collapse in stellar structures, Govender [25], in destruction of tumours, Andres and Pinnau [26], in drug delivery models, Ferreira and Oliveira [27], in describing how vegetation forms into patterns on landscapes, Consolo et al. [28, 29], in chemotaxis, Barbera and Valenti [30], in pollution, Barbera et al. [31], and other examples may be found in the book by Straughan [32].

Notable works on thermal convection using a Maxwell–Cattaneo model, some of which include magnetohydrodynamic effects are by Bissell [33], Eltayeb et al. [34], Hughes et al. [35], and Papanicolaou et al. [36]. Other treatments of the Cattaneo technique to include shock evolution, bifurcation theory, are by Jordan and Lambers [19].

The present work derives a novel model for thermal convection using Brinkman–Darcy–Kelvin–Voigt theory but we allow the heat flux to be of Maxwell–Cattaneo type. The novelties involve employing Guyer–Krumhansl theory in conjunction with Maxwell–Cattaneo theory, cf. Jou et al. [17], Van et al. [37]; splitting the heat flux into an instantaneous Fourier part and a memory part depending on the temperature gradient, using an extra flux idea of Mariano [38]; and allowing the heat flux equation to be objective, which necessarily introduces other terms, cf. Morro [39, 40]. Incorporation of Guyer–Krumhansl theory is pertinent since Van [37], Fulop et al. [41], suggest that this theory may be more relevant than Fourier theory, even at room temperatures, see also Berezovski [42, 43], Capriz et al. [44], Carlomagno et al. [45], Cimmelli [46], Fama et al. [47], Rogolino and Cimmelli [48].

A complete stability analysis for the Bénard problem for the Brinkman–Darcy–Kelvin–Voigt equations is presented here. In addition to a detailed linear instability analysis for both stationary and oscillatory convection we include a fully nonlinear energy stability analysis. Such analyses for systems incorporating Maxwell–Cattaneo effects have previously proved difficult, cf. Straughan [49, p. 192].

2 Basic equations

Let \(v_i(\mathbf{x},t),p(\mathbf{x},t),T(\mathbf{x},t)\) and \(Q_i(\mathbf{x},t)\) denote the velocity, pressure, temperature, and heat flux at position \(\mathbf{x}\) and time t. The Brinkman–Darcy–Kelvin–Voigt equations consist of a balance of momentum equation,

$$\begin{aligned} v_{i,t}-{{\hat{\lambda }}}\Delta v_{i,t}+v_jv_{i,j}=-\frac{1}{\rho }\,p_{,i}+\nu \Delta v_i+\alpha gk_iT-\mu _1 v_i, \end{aligned}$$
(1)

a balance of mass equation

$$\begin{aligned} v_{i,i}=0, \end{aligned}$$
(2)

a balance of energy equation

$$\begin{aligned} T_{,t}+v_iT_{,i}=-Q_{i,i}+\zeta \Delta T, \end{aligned}$$
(3)

and a Maxwell–Cattaneo like equation for the heat flux of form

$$\begin{aligned} \tau \,\frac{{{\mathcal {D}}}Q_i}{{{\mathcal {D}}}t}=-Q_i-\kappa T_{,i}+{\hat{\xi }_1}\Delta Q_i+{\hat{\xi }_2}Q_{k,ik}. \end{aligned}$$
(4)

In these equations \({{\hat{\lambda }}}\) is the Kelvin–Voigt coefficient, \(\rho \) is the constant density of the fluid, \(\nu \) is the kinematic viscosity, \(\alpha \) is the thermal expansion coefficient, g is gravity, \(\mathbf{k}=(0,0,1)\), \(\mu _1\) is the Darcy coefficient which is essentially the kinematic viscosity divided by the permeability of the porous medium, \(\zeta \) is a positive constant, \(\tau \) is the relaxation time, \(\kappa \) is the thermal diffusivity, and \({{\hat{\xi }}}_1,{{\hat{\xi }}}_2\) are the Guyer–Krumhansl coefficients. Throughout this article we employ standard indicial notation in conjunction with the Einstein summation convention, so for example,

$$\begin{aligned} v_{i,i}\equiv \sum _{i=1}^3\,\frac{\partial v_i}{\partial x_i}=&\frac{\partial v_1}{\partial x_1} +\frac{\partial v_2}{\partial x_2} +\frac{\partial v_3}{\partial x_3}\\ \equiv&\frac{\partial u}{\partial x} +\frac{\partial v}{\partial y} +\frac{\partial w}{\partial z} \end{aligned}$$

where \(\mathbf{v}\equiv (u,v,w)\) and \(\mathbf{x}\equiv (x,y,z)\). For a nonlinear example

$$\begin{aligned} v_iT_{,i}\equiv \sum _{i=1}^3v_i\,\frac{\partial T}{\partial x_i} \equiv u\,\frac{\partial T}{\partial x} +v\,\frac{\partial T}{\partial y} +w\,\frac{\partial T}{\partial z}. \end{aligned}$$

The term \(\Delta \) denotes the Laplacian in \({{\mathbb {R}}}^3\).

Equations (1)–(4) are defined on the horizontal layer \(\{(x,y)\in {\mathbb {R}}^2\}\times \{z\in (0,d)\}\) for \(t>0\). The boundary conditions are that

$$\begin{aligned} v_i=0,\,\,z=0,d;\quad T=T_L,\,\,z=0;\quad T=T_U,\,\,z=d;\quad Q_i=0,\,\,z=0,d; \end{aligned}$$
(5)

\(0<T_U<T_L\), with \(T_L,T_U\) constants.

Equation (3) is suggested by Payne and Song ([50], pp. 181–189), and I believe it may be justified from work of Mariano [38]. We interpret the \(\zeta \Delta T\) term to arise as an extra flux induced by the microstructure of the porous skeleton. If we assume \(v_i\equiv 0\) in Eqs. (3) and (4) then one may eliminate \(Q_i\) and one finds the temperature satisfies the equation

$$\begin{aligned} \tau \frac{\partial ^2T}{\partial t^2}-({{\hat{\xi }}}+\tau \zeta )\,\Delta \,\frac{\partial T}{\partial t} +\frac{\partial T}{\partial t} -(\zeta +\kappa )\Delta T+{{\hat{\xi }}}\zeta \Delta ^2T=0, \end{aligned}$$
(6)

where \({\hat{\xi }}={\hat{\xi }_1}+{\hat{\xi }_2}.\) Thus, the temperature field satisfies a second order in time differential equation but this equation is not hyperbolic. As the constants \({{\hat{\xi }}},\tau ,\zeta ,\kappa \) are positive the \(\partial T/\partial t\) terms lead to strong damping. Alternatively, we may think of the heat flux being in two parts as in Mariano [38], so the total heat flux is \(Q_i+F_i\) where \(Q_i\) is given by a Cattaneo—like evolution equation such as (4), whereas \(F_i=-\zeta T_{,i}\) is a Fourier term. If we do not include the Guyer–Krumhansl terms then the system becomes (when \(v_i\equiv 0\))

$$\begin{aligned} \begin{aligned}&T_{,t}=-Q_{i,i}-F_{i,i},\\&F_i=-\zeta T_{,i},\\&\tau Q_{i,t}+Q_i=-\kappa T_{,i}. \end{aligned} \end{aligned}$$
(7)

Equation (7)\(_3\) may be integrated employing an integrating factor, and assuming fading memory of \(T_{,i}\) we may show

$$\begin{aligned} Q_i=-\frac{\kappa }{\tau }\int _{-\infty }^t\exp \left( -\frac{t-s}{\tau }\right) \,T_{,i}\,ds. \end{aligned}$$

Thus, the total heat flux is

$$\begin{aligned} F_i+Q_i=-\zeta T_{,i}-\frac{\kappa }{\tau }\int _{-\infty }^t\exp \left( -\frac{t-s}{\tau }\right) \,T_{,i}\,ds, \end{aligned}$$

which is a viscoelastic—like term for the temperature gradient plus a term emphasizing the instantaneous temperature gradient. Such a representation is common in viscoelasticity, cf. Boltzmann [51], Miller [52], or for a modern appreciation of the work of Boltzmann see Markowitz [53]. Eliminating \(Q_i\) and \(F_i\) from (7) leads in this case to the equation

$$\begin{aligned} \tau \frac{\partial ^2T}{\partial t^2}-\tau \zeta \Delta \,\frac{\partial T}{\partial t} +\frac{\partial T}{\partial t} -(\zeta +\kappa )\Delta T=0. \end{aligned}$$
(8)

We choose a Guyer–Krumhansl theory in (4), cf. Jou et al. [17], Straughan [32], Van et al. [37], Fulop et al. [41]; recent interesting and inspiring articles dealing with Guyer–Krumhansl type theories, their generalizations to other areas in Continuum Mechanics, and novel applications are Berezovski [42, 43], Capriz et al. [44], Carlomagno et al. [45], Cimmelli [46], Fama [47], Rogolino and Cimmelli[48]. Indeed, Van et al. [37] is an interesting article containing experimental and theoretical work which suggests Guyer–Krumhansl theory may be more accurate than Fourier or traditional Maxwell–Cattaneo theory, even for temperatures typical of laboratory experiments.

In Eq. (4) the term \({{\mathcal {D}}}Q_i/{{\mathcal {D}}}t\) can possibly have several forms. One such form is the material derivative

$$\begin{aligned} \frac{{{\mathcal {D}}}Q_i}{{{\mathcal {D}}}t}=\frac{\partial Q_i}{\partial t}+v_j\frac{\partial Q_i}{\partial x_j}, \end{aligned}$$
(9)

and this derivative is shown to lead to a Galilean invariant theory by Christov and Jordan [54]. On the other hand Morro [39, 40] notes that (9) is not objective and therefore one should employ a suitable objective derivative. A general objective derivative is given by Morro [39, 40] as

$$\begin{aligned} \frac{{{\mathcal {D}}}Q_i}{{{\mathcal {D}}}t}=\frac{\partial Q_i}{\partial t}+v_j\frac{\partial Q_i}{\partial x_j}-W_{ij}Q_j+\gamma D_{ij}Q_j, \end{aligned}$$
(10)

where for our purposes \(\gamma \) is a constant, and

$$\begin{aligned} W_{ij}=\frac{1}{2}(v_{i,j}-v_{j,i}),\qquad D_{ij}=\frac{1}{2}(v_{i,j}+v_{j,i}). \end{aligned}$$

It may be enlightening to employ (10) in a complete analysis of thermal convection, but we here follow Christov [55] and employ a Lie derivative for which \(\gamma =-1\). This derivative was employed by Ciarletta and Straughan [56] and Tibullo and Zampoli [57], and by Bissell [33], Eltayeb et al. [34], Hughes et al. [35]. The resulting theory employing (10) with \(\gamma =-1\) is often referred to as Cattaneo–Christov theory. It is of interest to note that Morro [39] describes various objective derivatives and he observes that the form of derivative in (10) with \(\gamma =-1\) was suggested by Truesdell [58]. Furthermore, Straughan ([32], pp. 22–24) observes that employing a relaxation effect like that in (4) was suggested by Graffi [59] in the context of electromagnetism. Thus, when a relaxation theory is employed with an objective derivative (10) where \(\gamma =-1\), such a theory could be associated with the names of Graffi and Truesdell.

In this work we now employ (4) with \({\mathcal D}Q_i/{{\mathcal {D}}}t\) given by (10) with \(\gamma =-1\). For clarity we write Eq. (4) in this case as

$$\begin{aligned} \tau \,(Q_{i,t}+v_jQ_{i,j}-v_{i,j}Q_j)=-Q_i-\kappa T_{,i}+{\hat{\xi }_1}\Delta Q_i+{\hat{\xi }_2}Q_{k,ik}. \end{aligned}$$
(11)

The steady conduction solution to Eqs. (1), (2), (3), (11) and (5) in whose stability we are interested has form

$$\begin{aligned} {{\bar{v}}_i}\equiv 0,\qquad {{\bar{T}}}=T_L-\beta z,\qquad {\bar{\mathbf{Q}}}=(0,0,\kappa \beta ), \end{aligned}$$
(12)

where \(\beta \) is the temperature gradient,

$$\begin{aligned} \beta =\frac{T_L-T_U}{d}\,>\,0. \end{aligned}$$

The steady pressure is a quadratic function of z determined from (1).

3 Thermal convection

To analyse the instability/stability of the steady solution (12) we define perturbation variables \(u_i,\theta ,q_i,\pi \) by

$$\begin{aligned} v_i={{\bar{v}}}_i+u_i,\qquad T={{\bar{T}}}+\theta ,\qquad Q_i={\bar{Q}}_i+q_i,\qquad p={{\bar{p}}}+\pi . \end{aligned}$$

These expressions are substituted into Eqs. (1), (2), (3) and (4) and are non-dimensionalized with the scalings

$$\begin{aligned}&x_i=x_i^*d,\qquad t=\mathcal{T}t^*,\qquad \mathcal{T}=\frac{d^2}{\nu },\\&u_i=u_i^*U,\qquad \theta =\theta ^*T^{\sharp },\qquad q_i=q_i^*Q^{\sharp },\qquad \pi =\pi ^*P\,\\&U=\frac{\nu }{d},\qquad Pr=\frac{\nu }{\kappa },\qquad T^{\sharp }=U\sqrt{\frac{\beta \nu }{\alpha g\kappa }}\, \qquad Q^{\sharp }=\frac{T^{\sharp }\kappa }{d}\,\\&\xi _1=\frac{{\hat{\xi }_1}Q^{\sharp }}{d\kappa T^{\sharp }},\qquad \xi _2=\frac{{\hat{\xi }_2}Q^{\sharp }}{d\kappa T^{\sharp }},\qquad \xi =\frac{\mu _1d^2}{\nu },\\&P=\frac{\rho \nu U}{d},\qquad Sg=\frac{\tau \nu }{d^2}, \end{aligned}$$

where Sg is a parameter introduced in Papanicolaou et al. [36]. The Rayleigh number Ra is introduced as

$$\begin{aligned} Ra\equiv R^2=\frac{\beta g\alpha d^4}{\nu \kappa }. \end{aligned}$$

In this way we arrive at the non-dimensional perturbation equations, where the *s are dropped,

$$\begin{aligned} \begin{aligned}&u_{i,t}-\lambda \Delta u_{i,t}+u_ju_{i,j}=-\pi _{,i}+\Delta u_i+R\theta k_i-\xi u_i,\\&u_{i,i}=0,\\&Pr(\theta _{,t}+u_i\theta _{,i})=Rw-q_{i,i}+\zeta \Delta \theta ,\\&Sg(q_{i,t}+u_jq_{i,j}-u_{i,j}q_j)=RPrSg\,u_{i,3}-q_i-\theta _{,i}+\xi _1\Delta q_i+\xi _2 q_{k,ki}, \end{aligned} \end{aligned}$$
(13)

where (13) hold on \({\mathbb {R}}^2\times (0,1)\times \{t>0\}\), with \(w\equiv u_3\).

Care must be taken with the boundary conditions when Guyer–Krumhansl terms are present. The non-dimensional perturbation boundary conditions we employ are

$$\begin{aligned} u_i=0,\quad z=0,1;\qquad \theta =0,\quad z=0,1; \qquad q_i=0,\quad z=0,1; \end{aligned}$$
(14)

or

$$\begin{aligned} \begin{aligned}&u_i=0,\quad z=0,1;\qquad \theta =0,\quad z=0,1;\\&\qquad q_1=q_2=0,\quad z=0,1; \qquad q_{3,3}=0,\quad z=0,1; \end{aligned} \end{aligned}$$
(15)

together with horizontal periodicity of the solution, cf. Straughan ([49], p. 51). The period cell of the solution is denoted by V. When we use (15) one additionally requires \(\int _Vq_3dx=0\), to exclude constant vertical heat flux perturbations.

4 Linear instability

To develop a linear instability analysis for (13) and (14) we drop the quadratic terms and introduce a time dependence like

$$\begin{aligned} u_i=e^{\sigma t}u_i(\mathbf{x}),\quad \theta =e^{\sigma t}\theta (\mathbf{x}),\quad q_i=e^{\sigma t}q_i(\mathbf{x}),\quad \pi =e^{\sigma t}\pi (\mathbf{x}), \end{aligned}$$

and we then have an eigenvalue problem for the growth rate \(\sigma \). To solve this eigenvalue problem for fixed boundary conditions results in a heavy numerical computation. One must take curlcurl of (13)\(_1\) and then one is left with solving three fourth order equations for \(u,v,w\,\,(\equiv \,\,(u_1,u_2,u_3))\), three second order equations for \(q_1,q_2,q_3\), and one second order equation for \(\theta \). We thus need twenty boundary conditions. Sixteen of these follow from (5) and (2) and are

$$\begin{aligned}&w=0,\quad \frac{\partial w}{\partial z}=0,\quad \theta =0,\quad q_1=0,\\&q_2=0,\quad q_3=0,\quad u=0,\quad v=0,\qquad z=0,1. \end{aligned}$$

To determine the remaining four boundary conditions we take curlcurl of (13)\(_1\) and evaluate the result for components 1 and 2 on the boundaries \(z=0,1\). In this way one derives the further four conditions as

$$\begin{aligned}&-\sigma (v_{,z}+\lambda w_{,yzz}-\lambda v_{,zxx}-\lambda v_{,zyy}-\lambda v_{,zzz}) +w_{,yzz}-v_{,zxx}-v_{,zyy}-v_{,zzz}=0,\quad \\&z=0,1, \end{aligned}$$

and

$$\begin{aligned}&-\sigma (u_{,z}+\lambda w_{,xzz}-\lambda u_{,zxx}-\lambda u_{,zyy}-\lambda u_{,zzz}) +w_{,xzz}-u_{,zxx}-u_{,zyy}-u_{,zzz}=0,\quad \\&z=0,1. \end{aligned}$$

Since this is the first analysis of the convection model presented here we solve Eq. (13) subject to stress free surface boundary conditions, as is done in e.g. Eltayeb et al. [34], Hughes et al. [35].

The condition \(n_j\sigma _{ij}=0\) on \(z=0,1,\) reduces to

$$\begin{aligned} u_{,z}=v_{,z}=0,\qquad \mathrm{on}\quad z=0,1, \end{aligned}$$

and then with the continuity equation one sees that

$$\begin{aligned} w_{,zz}=0,\qquad \mathrm{on}\quad z=0,1. \end{aligned}$$

We also require

$$\begin{aligned} w=0,\,\,\theta =0,\,\,q_1=0,\,\,q_2=0,\,\,q_{3,3}=0,\qquad \mathrm{on}\,\, z=0,1. \end{aligned}$$

For linear instability we then reduce Eq. (13) to

$$\begin{aligned} \begin{aligned}&\sigma (-\Delta w+\lambda \Delta ^2w)+\Delta ^2w+R\Delta ^*\theta -\xi \Delta w=0,\\&Pr\sigma \theta -\zeta \Delta \theta -Rw+\Gamma =0,\\&(Sg\sigma +1)\Gamma +\Delta \theta -\epsilon \Delta \Gamma =0, \end{aligned} \end{aligned}$$
(16)

where \(\Delta ^*=\partial ^2/\partial x^2+\partial ^2/\partial y^2,\) \(\Gamma =q_{i,i},\) and \(\epsilon =\xi _1+\xi _2.\) For stress free boundary conditions we may show from (16) that \(w,\theta \) and \(\Gamma \) may be represented by sin series of form \(w=\sum _{n=1}^{\infty }w_n\,sin\,n\pi z\), with a similar form for \(\theta ,\Gamma \).

The stationary convection boundary is found by evaluating a determinant derived from (16) to be

$$\begin{aligned} R^2=\frac{1}{a^2}\,\Bigl [\zeta \Lambda ^2(\Lambda +\xi )+\frac{\Lambda ^3+\xi \Lambda ^2}{(1+\epsilon \Lambda )}\Bigr ], \end{aligned}$$
(17)

where \(\Lambda =\pi ^2+a^2,\) with a being the wavenumber. (Actually, \(\Lambda =n^2\pi ^2+a^2,\) but it may be shown \(n=1\) yields the minimum.) The critical values of the Rayleigh number for stationary convection, \(Ra_{stat}=R^2_{stat},\) are then found by minimizing numerically \(R^2\) in (17) in \(a^2.\)

To find the oscillatory convection boundary we put \(\sigma =i\omega \), \(\omega \in {\mathbb {R}}\), in (16), and then solve a determinant equation which yields a cubic in \(\sigma \). The real and imaginary parts of this equation are resolved and the oscillatory convection Rayleigh number, \(R^2_{osc},\) may be shown to follow from

$$\begin{aligned} R^2_{osc}=\frac{A}{a^2Sg^2B}, \end{aligned}$$
(18)

where

$$\begin{aligned} A=&Pr^2\Lambda \Gamma _2\Gamma _3(\Gamma _1\Gamma _2+Sg\Gamma _3)+\Lambda ^2\Gamma _1^2Pr\Gamma _2+Sg\zeta \Lambda \\&+\Lambda ^2\zeta (\Gamma _1\Gamma _2+Sg\Gamma _3)(Pr\Gamma _1\Gamma _2+SgPr\Gamma _3+Sg\zeta \Lambda \Gamma _1), \end{aligned}$$

and

$$\begin{aligned} B=Pr\Gamma _3+\zeta \Lambda \Gamma _1, \end{aligned}$$

with

$$\begin{aligned} \Lambda =\pi ^2+a^2,\quad \Gamma _1=1+\lambda \Gamma ,\quad \Gamma _2=1+\epsilon \Lambda ,\quad \Gamma _3=\Lambda +\xi . \end{aligned}$$

The critical values of the Rayleigh number for oscillatory convection may be found by minimizing \(R^2_{osc}\) from (18) in \(a^2\).

Remark 1

It is worth pointing out that for linear instability via stationary or oscillatory convection the results obtained here for the Lie derivative where \(\gamma =-1\) in (10) are exactly the same as would be obtained if we had employed a material derivative for \(Q_i\) in (4). Of course, the nonlinear theory is different in both cases. The point here is that if we had not employed a Truesdell derivative in (10), i.e. had we selected a value of \(\gamma \ne -1\), then even in the linearized theory the results are different from when one simply employs the material derivative.

5 Nonlinear stability

Let \(\Vert \cdot \Vert \) and \((,\cdot ,)\) denote the norm and inner product on \(L^2(V).\) Further, let \(\Vert \cdot \Vert _q\) be the norm on \(L^q(V)\) where we omit the index when \(q=2\).

To investigate nonlinear stability of (12), we multiply (13)\(_1\) by \(u_i\), (13)\(_3\) by \(\theta \), (13)\(_4\) by \(q_i\), and integrate each over a period cell V. After some integrations by parts and use of the boundary conditions we may obtain the identities,

$$\begin{aligned} \frac{d}{dt}\Bigl (\frac{1}{2}\Vert \mathbf{u}\Vert ^2+\frac{\lambda }{2}\Vert \nabla \mathbf{u}\Vert ^2\Bigr )= R(\theta ,w)-\xi \Vert \mathbf{u}\Vert ^2-\Vert \nabla \mathbf{u}\Vert ^2, \end{aligned}$$
(19)

and

$$\begin{aligned} \frac{d}{dt}\frac{Pr}{2}\Vert {\theta }\Vert ^2= R(\theta ,w)-(q_{i,i},\theta )-\zeta \Vert \nabla {\theta }\Vert ^2, \end{aligned}$$
(20)

and

$$\begin{aligned} \begin{aligned} \frac{d}{dt}\frac{Sg}{2}\Vert \mathbf{q}\Vert ^2&= Sg(u_{i,j},q_iq_j)-\Vert \mathbf{q}\Vert ^2-(\theta _{,i},q_i)\\&\quad -\xi _1\Vert \nabla \mathbf{q}\Vert ^2-\xi _2\Vert \Gamma \Vert ^2 +RSgPr(u_{i,3},q_i). \end{aligned} \end{aligned}$$
(21)

By addition of these equations and integration by parts on the \((\theta _{,i},q_i)\) term we may arrive at the energy equation

$$\begin{aligned} \frac{dE}{dt}=RI-D_E+N, \end{aligned}$$
(22)

where the energy function is given by

$$\begin{aligned} E=\frac{1}{2}\Vert \mathbf{u}\Vert ^2+\frac{\lambda }{2}\Vert \nabla \mathbf{u}\Vert ^2+\frac{Pr}{2}\Vert \theta \Vert ^2+\frac{Sg}{2}\Vert \mathbf{q}\Vert ^2, \end{aligned}$$
(23)

the dissipation, \(D_E\), is

$$\begin{aligned} D_E=\Vert \nabla \mathbf{u}\Vert ^2+\xi \Vert \mathbf{u}\Vert ^2+\zeta \Vert \nabla \theta \Vert ^2+\Vert \mathbf{q}\Vert ^2 +\xi _1\Vert \nabla \mathbf{q}\Vert ^2+\xi _2\Vert \Gamma \Vert ^2, \end{aligned}$$
(24)

the production term has form

$$\begin{aligned} I=2(\theta ,w)+PrSg(u_{i,3},q_i), \end{aligned}$$
(25)

and where the cubic nonlinearity has form

$$\begin{aligned} N=Sg(u_{i,j},q_iq_j). \end{aligned}$$
(26)

We henceforth discard the \(\xi _2\) term and work with the following energy inequality [which follows from (22)],

$$\begin{aligned} \frac{dE}{dt}\le RI-D+N, \end{aligned}$$
(27)

where the dissipation function, D, is given by

$$\begin{aligned} D=\Vert \nabla \mathbf{u}\Vert ^2+\xi \Vert \mathbf{u}\Vert ^2+\zeta \Vert \nabla \theta \Vert ^2+\Vert \mathbf{q}\Vert ^2 +\xi _1\Vert \nabla \mathbf{q}\Vert ^2. \end{aligned}$$
(28)

Define \(R_E\) by

$$\begin{aligned} \frac{1}{R_E}=\max _H\,\frac{I}{D}, \end{aligned}$$
(29)

where \(H=\{u_i,\theta ,q_i\in H^1_0(V):\, u_{i,i}=0\}\) is the space of admissible solutions.

To obtain nonlinear stability from (27) we obtain

$$\begin{aligned} \frac{dE}{dt}=-D\Bigl (1-\frac{R}{R_E}\Bigr )+N, \end{aligned}$$
(30)

and we suppose now \(R<R_E\). To handle the cubic nonlinear term we use the Cauchy–Schwarz inequality to find

$$\begin{aligned} N\le Sg\Vert \nabla \mathbf{u}\Vert \,\Vert \mathbf{q}\Vert ^2_4, \end{aligned}$$

and then we employ the Sobolev inequality \(\Vert \mathbf{q}\Vert _4\le c_1^{1/2}\Vert \nabla \mathbf{q}\Vert \) to derive

$$\begin{aligned} N\le c_1Sg\Vert \nabla \mathbf{u}\Vert \,\Vert \nabla \mathbf{q}\Vert ^2, \end{aligned}$$
(31)

where \(c_1\) is a constant depending on V. Then from (30) one deduces

$$\begin{aligned} \frac{dE}{dt}\le -D\Bigl (1-\frac{R}{R_E}\Bigr )+cE^{1/2}D, \end{aligned}$$
(32)

where \(c=c_1Sg2^{1/2}/(\xi \lambda ^{1/2}).\) Since \(R<R_E\) we put \(b=1-R/R_E>0\) and then it follows that

$$\begin{aligned} \frac{dE}{dt}\le -D(b-cE^{1/2}). \end{aligned}$$
(33)

Provided \(E^{1/2}(0)<b/c\) one may employ a continuity argument to show, cf. Straughan [49, pp. 15–16],

$$\begin{aligned} E(t)\le \exp (-ht)E(0), \end{aligned}$$
(34)

where \(h=\pi ^2(b-cE^{1/2}(0).\)

Hence, we have demonstrated nonlinear stability in the E measure provided

$$\begin{aligned} R<R_E\quad \mathrm{and}\quad E^{1/2}(0)< \frac{b}{c}. \end{aligned}$$
(35)

To find \(R_E\) we obtain the Euler–Lagrange equations from (29)as

$$\begin{aligned} \begin{aligned}&\Delta u_i-\xi u_i+R_E\theta k_i-\frac{R_E}{2}\,PrSg\,q_{i,3}=\ell _{,i},\\&u_{i,i}=0,\\&\zeta \Delta \theta +R_E\,w=0,\\&\xi _1\Delta q_i-q_i+\frac{R_E}{2}\,PrSg\,u_{i,3}=0, \end{aligned} \end{aligned}$$
(36)

where \(\ell \) is a Lagrange multiplier.

We solve Eq. (36) for stress free boundary conditions. In this case we reduce Eq. (36) to

$$\begin{aligned} \begin{aligned}&-\Delta ^2w+\xi \Delta w-R_E\Delta ^*\theta -\frac{R_E}{2}\,PrSg\,(\Gamma _{,33}-\Delta q_{3,3})=0,\\&\zeta \Delta \theta +R_E\,w=0,\\&\xi _1\Delta q_3-q_3+\frac{R_E}{2}\,PrSg\,w_{,3}=0,\\&\epsilon \Delta \Gamma -\Gamma =0. \end{aligned} \end{aligned}$$
(37)

The term \(\Delta q_{3,3}\) is eliminated from (37)\(_1\) and the remaining equations may be reduced to the relation,

$$\begin{aligned} R_E^2=\frac{\zeta \Lambda ^2(\Lambda +\xi )(1+\xi _1\Lambda )}{a^2(1+\xi _1\Lambda )+0.25 Pr^2Sg^2\zeta \Lambda ^2\pi ^2}. \end{aligned}$$
(38)

The critical Rayleigh number of nonlinear stability is determined by minimizing (38) in \(a^2\).

Remark 2

We have discarded the \(\xi _2\) term in the analysis leading to (27). This term may be retained but the resulting analysis of the subsequent Euler–Lagrange system is substantially more involved and leads to very little improvement in the stability threshold. Since this is the first analuysis of this system we prefer to employ the simpler argument and not obscure the physical highlights with technical details.

Remark 3

If we had employed a material derivative for \(Q_i\) in (4) rather than the form (11) then the energy stability results would be for global stability instead of the conditional result here, see (35).

6 Unconditional nonlinear stability

It is of interest to observe that we may obtain a result of unconditional nonlinear stability (i.e. for all initial data) from Eq. (13). To achieve this we replace (13)\(_4\) by differentiating that equation by \(\partial /\partial x_i\) to obtain the evolution equation for \(\Gamma \) as

$$\begin{aligned} Sg(\Gamma _{,t}+u_j\Gamma _{,j})=-\Gamma -\Delta \theta +\epsilon \Delta \Gamma . \end{aligned}$$
(39)

One now works with the energy identities (19), (20), and the equation obtained by multiplying (39) by \(\Gamma \) and integrating over V (where we are assuming \(q_{3,3}=0\) on \(z=0,1\), ), namely

$$\begin{aligned} \frac{d}{dt}\frac{Sg}{2}\Vert \Gamma \Vert ^2=-\Vert \Gamma \Vert ^2+(\nabla \theta ,\nabla \Gamma )-\epsilon \Vert \nabla \Gamma \Vert ^2. \end{aligned}$$
(40)

We now add (19), (20) and (40) to see that

$$\begin{aligned} \frac{dF}{dt}\le I_F-D_F, \end{aligned}$$
(41)

where the energy function, F, is now

$$\begin{aligned} F(t)=\frac{1}{2}\Vert \mathbf{u}\Vert ^2+\frac{\lambda }{2}\Vert \nabla \mathbf{u}\Vert ^2+\frac{Pr}{2}\Vert \theta \Vert ^2+\frac{Sg}{2}\Vert \Gamma \Vert ^2, \end{aligned}$$
(42)

while

$$\begin{aligned} I_F=2R(\theta ,w)-(\Gamma ,\theta )+(\nabla \theta ,\nabla \Gamma ), \end{aligned}$$
(43)

whereas,

$$\begin{aligned} D_F=\Vert \Gamma \Vert ^2+\epsilon \Vert \nabla \Gamma \Vert ^2+\zeta \Vert \nabla \theta \Vert ^2+\xi \Vert \mathbf{u}\Vert ^2+\Vert \nabla \mathbf{u}\Vert ^2. \end{aligned}$$
(44)

Define now

$$\begin{aligned} R_U=\max _{H}\,\frac{I_F}{D_F}, \end{aligned}$$
(45)

where H is the space of admissible solutions and then from (41) one may find

$$\begin{aligned} \frac{dF}{dt}\le -D_F\Bigl (1-\frac{1}{R_U}\Bigr ). \end{aligned}$$
(46)

Suppose now \(1<R_U\) and put \(b_3=1-1/R_U>0\). Then, from (46) one may show that

$$\begin{aligned} \frac{dF}{dt}\le -b_3D_F. \end{aligned}$$
(47)

Inequality (47) is integrated after use of Poincaré’s inequality on \(D_F\) to see that

$$\begin{aligned} F(t)\le F(0)\exp (-c_3t), \end{aligned}$$
(48)

for a constant \(c_3\) depending on \(b_3\). Unconditional nonlinear stability ensues from inequality (48).

The limit for \(R_U\) is \(R_U=1\) and this yields the energy stability threshold. Henceforth, we take \(R_U=1\). The Euler–Lagrange equations arising from (45) with \(R_U=1\) are

$$\begin{aligned}&\Delta u_i-\xi u_i+R\theta k_i=\ell _{,i},\\&\zeta \Delta \theta +Rw-\frac{1}{2}\Gamma -\frac{1}{2}\Delta \Gamma =0,\\&\epsilon \Delta \Gamma +Rw-\frac{1}{2}\theta -\frac{1}{2}\Delta \theta =0, \end{aligned}$$

and from these equations we deduce, for two stress free surfaces,

$$\begin{aligned} R_{unc}^2=\frac{\zeta (\Lambda ^3+\xi \Lambda ^2)}{a^2}-\frac{(1-\Lambda )^2(\Lambda ^2+\xi \Lambda )}{4a^2(1+\epsilon \Lambda )}. \end{aligned}$$
(49)

The unconditional energy stability limit may be found by minimizing \(R_{unc}^2\) in \(a^2\). It is straightforward to show that \(R^2_{stat}\ge R_{unc}^2\) and some numerical results for the unconditional critical Rayleigh number, \(Ra_{unc}\), are given in Sect. 7. The results for the unconditional critical Rayleigh number are less than the linear instability threshold, although they do represent a bound for global nonlinear stability. As \(\zeta \) increases \(Ra_{unc}\) becomes much closer to \(Ra_{stat}\), the linear stationary convection threshold.

Remark 4

One may develop another energy estimate by employing (19), (40), then multiplying (13)\(_3\) by \(-\Delta \theta \) and integrating over V. This avoids the \(\Gamma \) and \(\theta \) quadratic terms in (41), and would lead to a sharper Rayleigh number threshold than (49). In this case one derives an “energy" equation of form

$$\begin{aligned} \frac{dE}{dt}=RI-D+N, \end{aligned}$$

where

$$\begin{aligned}&E=\frac{1}{2}\Vert \mathbf{u}\Vert ^2+\frac{\lambda }{2}\Vert \nabla \mathbf{u}\Vert ^2+\frac{Pr}{2}\Vert \nabla \theta \Vert ^2 +\frac{Sg}{2}\Vert \Gamma \Vert ^2,\\&I=(\theta ,w)-(\nabla w,\nabla \theta ),\\&D=\xi \Vert \mathbf{u}\Vert ^2+\Vert \nabla \mathbf{u}\Vert ^2+\Vert \Gamma \Vert ^2+\epsilon \Vert \nabla \Gamma \Vert ^2+\zeta \Vert \Delta \theta \Vert ^2, \end{aligned}$$

and the cubic nonlinearity has form

$$\begin{aligned} N=-Pr\int _{V}u_{i,j}\theta _{,i}\theta _{,j}\,dx. \end{aligned}$$

The drawback with this is that the nonlinear stability so obtained is conditional.

7 Numerical results

Numerical results are now reported based on minimization of expressions (17), (38), (49) and (18), yielding the critical Rayleigh and wave numbers of stationary convection, nonlinear energy stability, unconditional nonlinear stability, and oscillatory convection, \(Ra_{stat}\), \(Ra_{en}\), \(Ra_{unc}\), \(Ra_{osc}\), \(a^2_{stat}\), \(a^2_{en}\), \(a^2_{unc}\), \(a^2_{osc}\), respectively. We include some results for the unconditional nonlinear stability threshold in Table 1, where \(Ra_{unc}\) and \(a^2_{unc}\) denote the relevant critical Rayleigh and wave numbers obtained from (49). We have computed many results and a small selection are displayed because we have to vary over the parameters \(Pr,\lambda ,Sg,\xi ,\xi _1,\xi _2\) and \(\zeta \). Tables 1, 2 and 3 give values of \(Ra_{stat}\), \(a^2_{stat}\), \(Ra_{en}\), \(a^2_{en}\), \(Ra_{unc}\), \(a^2_{unc}\), \(Ra_{osc}\), \(a^2_{osc}\). In all tables we take \(Pr=6\). Table 1 selects \(\lambda =0.1,\xi =0.1,\xi _2=0.1,Sg=10^{-2}\), and \(\zeta \) varies over 0.6–1.4, while \(\xi _1\) varies over 0.5, 1, 1.5, 2, 2.5 and 1000 as shown in the table. Tables 2 and 3 use the same variation for \(\zeta \) and \(\xi _1\) but not for \(\xi _1=1000\), and take \(\lambda =0.1,\xi =1,\xi _2=1,Sg=10^{-3}\), and \(\lambda =10^{-2},\xi =10,\xi _2=10^{-2},Sg=10^{-4}\), respectively. We have computed with \(\xi _1\) ranging from 0.5 to 1000 to check on the behaviour for large \(\xi _1\).

Table 1 Critical values of Rayleigh and wave numbers for stationary, oscillatory, and energy stability
Full size table
Table 2 Critical values of Rayleigh and wave numbers for stationary, oscillatory, and energy stability
Full size table
Table 3 Critical values of Rayleigh and wave numbers for stationary, oscillatory, and energy stability. \(Pr=6\), \(\lambda =0.01\), \(Sg=0.0001\), \(\xi =10\), \(\xi _2=0.01\), with \(\zeta \) and \(\xi _1\) values as shown in the table
Full size table
Fig. 1
figure 1

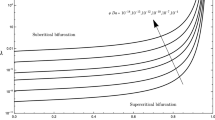
Critical values of Rayleigh numbers for stationary convection, \(Ra_{stat},\) energy stability, \(Ra_{energy},\) and unconditional energy stability, \(Ra_{uncond},\) against \(\xi _1\). The other parameters have values \(Pr=6\), \(\zeta =1\), \(\lambda =0.1\), \(Sg=0.01\), \(\xi =0.1\), \(\xi _2=0.1\)

Full size image

We observe that

$$\begin{aligned} a^2(1+\xi _1\Lambda )+\frac{Pr^2Sg^2\zeta \Lambda ^2\pi ^2}{4}\,\ge \, a^2(1+\xi \Lambda ), \end{aligned}$$

and then from (38),

$$\begin{aligned} R^2_{en}&= \frac{\zeta \Lambda ^2(\Lambda +\xi )(1+\xi _1\Lambda )}{a^2(1+\xi _1\Lambda )+(Pr^2Sg^2\zeta \Lambda ^2\pi ^2/4)}\\&\le \, \frac{\zeta \Lambda ^2(\Lambda +\xi )}{a^2}\\&\le \, \frac{1}{a^2}\Bigl [\zeta \Lambda ^2(\Lambda +\xi )+\frac{\Lambda ^3+\xi \Lambda ^2}{1+\epsilon \Lambda }\Bigr ],\\&=\,Ra^2_{stat}, \end{aligned}$$

where (17) is recognized. Thus, we know

$$\begin{aligned} R^2_{en}\le R^2_{stat}, \end{aligned}$$

as it should be.

Firstly, from Tables 1, 2 and 3 we observe that for Sg in the range \(10^{-2}\)–\(10^{-4}\) oscillatory convection will not be observed. It is possible to witness oscillatory convection, but Sg has to be much larger, perhaps of order 100, and then \(a^2_{osc}\) is very small. Consolo [28, 29] do suggest \(\tau \) values large enough for Sg in the range \(O(10^2)\), and hence oscillatory convection may not be negligible in all cases. We should point out that the Kelvin–Voigt parameter is only instrumental in the oscillatory convection case, although it is essential in the nonlinear theory.

From Tables 1, 2 and 3 we note that the variation in \(Ra_{stat}\), \(Ra_{en}\), and \(Ra_{unc}\) is significant as \(\zeta \) increases. Indeed, \(Ra_{stat}\), \(Ra_{en}\) and \(Ra_{unc}\) increase substantially with increasing \(\zeta \) and this means the system is more stable and convective motion commences less easily. On the other hand, as \(\xi _1\) increases \(Ra_{stat}\) decreases, but \(Ra_{en}\) and \(Ra_{unc}\) increase, but the variation is less than that observed with \(\zeta \) varying. As \(\xi _1\) increases the nonlinear values, \(Ra_{en}\), \(Ra_{unc}\), become much closer to \(Ra_{stat}\), as may be seen in Tables 1, 2 and 3, and as shown in Fig. 1.

8 Conclusions

We have introduced a new model for thermal convection of a Kelvin– Voigt viscoelastic fluid in a Darcy–Brinkman porous material with the temperature field being governed by a procedure suggested by [50], and incorporating Maxwell–Cattaneo–Guyer–Krumhansl theory of heat flow. Attention is given to which derivative is employed for the heat flux since this may affect the instability values for convective motion substantially.

Linear instability values and nonlinear stability thresholds are calculated for the case of two stress free surfaces, and in addition to a thorough analysis of stationary and oscillatory convection, an exact nonlinear analysis is included. We have not seen such a nonlinear analysis for a model employing Maxwell–Cattaneo theory previously.

Remark 5

We have dealt here with the Brinkman–Darcy–Kelvin– Voigt system of equations. The mathematical structure of the Navier–Stokes–Voigt equations with a linear friction term is exactly the same as Eqs. (1), (2), (3) and (4), cf. DiPlinio et al. [60], provided we employ the thermal structure as introduced in Payne and Song [50] and as used here. DiPlinio et al. [60] analyse an analogous isothermal system, although they also include an extra viscoelastic memory term. In the pure fluid case, the \(-\lambda \Delta u_{i,t}\) term represents the Kelvin–Voigt part in the Navier–Stokes–Voigt equations and the \(-\xi u_i\) piece is the Rayleigh friction contribution.