Optimal mean–variance selling strategies

Abstract

Assuming that the stock price X follows a geometric Brownian motion with drift $\mu \in \mathbb {R}$ and volatility $\sigma >0$, and letting $\mathsf {P}_{\!x}$ denote a probability measure under which X starts at $x>0$, we study the dynamic version of the nonlinear mean–variance optimal stopping problem

$$\begin{aligned} \sup _\tau \Big [ \mathsf {E}\,\!_{X_t}(X_\tau ) - c\, \mathsf {V}ar\,\!_{\!X_t}(X_\tau ) \Big ] \end{aligned}$$

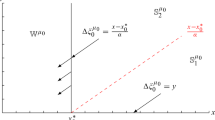
where t runs from 0 onwards, the supremum is taken over stopping times $\tau$ of X, and $c>0$ is a given and fixed constant. Using direct martingale arguments we first show that when $\mu \le 0$ it is optimal to stop at once and when $\mu \ge \sigma ^2\!/2$ it is optimal not to stop at all. By employing the method of Lagrange multipliers we then show that the nonlinear problem for $0 < \mu < \sigma ^2\!/2$ can be reduced to a family of linear problems. Solving the latter using a free-boundary approach we find that the optimal stopping time is given by

$$\begin{aligned} \tau _* = \inf \,\! \left\{ \, t \ge 0\; \vert \; X_t \ge \tfrac{\gamma }{c(1-\gamma )}\, \right\} \end{aligned}$$

where $\gamma = \mu /(\sigma ^2\!/2)$. The dynamic formulation of the problem and the method of solution are applied to the constrained problems of maximising/minimising the mean/variance subject to the upper/lower bound on the variance/mean from which the nonlinear problem above is obtained by optimising the Lagrangian itself.