First-Principles Calculations of Spinodal Ordering Temperature and Diffuse Intensity Scattering Spectrum for Fe-Pt System

Abstract

First-principles calculations are performed to derive a L1₀-disorder phase diagram, spinodal ordering temperature and short-range-order diffuse-intensity spectrum for the Fe-Pt system. L1₀-disorder transition is confirmed to be of the first order by both the temperature dependence of the long-range-order parameter and the large separation between the transition temperature and spinodal ordering temperature. Short-range-order diffuse-intensity maximum appears at 〈100〉 which is intensified as the spinodal-ordering temperature is approached. The consistency among all these results supports the reliability of the description of the cluster variation free energy used for this study.

Introduction

It is essential to employ an accurate free energy model to derive a reliable phase diagram. The accuracy of a calculated phase diagram is often assessed by the comparison with an experimental phase diagram, where a particular focus is placed on agreements/disagreements of transition temperatures, invariant temperatures and corresponding compositions.

It should be noted that a free energy formulae is supposed to convey much more affluent information than that required to calculate a phase diagram which is determined by a vanishing condition of the first order derivative. In fact, the second order derivative provides information concerning the intrinsic stability of a given system against the fluctuation, and vanishing condition of the second-order derivative yields the locus of spinodal-ordering temperature.[1] Furthermore, the inverse of the second order derivative matrix in the Fourier space gives a short range order (SRO) diffuse-intensity spectrum which is directly comparable with a scattering experiment.

It is claimed that a reliable free energy model should be able to derive this information in a consistent manner from a single free energy formula. Among various free energy models, it has been amply demonstrated that the cluster variation method (CVM)[2] satisfies this criterion. In fact, the author and his coworkers performed first-principles investigations on the phase equilibria of a series of noble metal alloys and calculated phase diagrams, locus of spinodal-ordering temperatures and short-range-order diffuse-intensity spectra based on CVM.[3,4]

Recently, the author and his coworkers have performed first-principles calculations of L1₀-disorder phase boundary in a series of Fe-based alloys including Fe-Ni, Fe-Pd and Fe-Pt systems.[5–8] And it has been demonstrated that the L1₀-disorder transition temperatures were obtained with very high accuracy for Fe-Pd and Fe-Pt systems. For Fe-Ni system, the first-principles calculations revealed[9] the existence of an L1₀ ordered phase although this phase has been missing in the conventional phase diagram.

The primary objective of the present study is to calculate spinodal-ordering temperature and short-range-order diffuse-intensity spectra associated with disorder-L1₀ transition of Fe-Pt system by applying the theoretical procedure employed for the noble metal alloys.[4] The organization of the present report is as follows. In the next section, for the sake of completeness, theoretical procedure of calculating a phase diagram, spinodal-ordering temperature and short-range-order diffuse-intensity spectrum, are reviewed. Then the results are presented and discussed in the third section.

Theoretical Procedure of First-Principles Calculations

Phase Equilibria Calculations

The free energy of formation of a phase n is formally given as

$$ \Updelta F^{\left( n \right)} \left( {r,T} \right) = \Updelta E_{\text{el}}^{\left( n \right)} \left( r \right) + \Updelta E_{\text{vib}}^{\left( n \right)} \left( {r,T} \right) - T \cdot \Updelta S_{\text{vib}}^{\left( n \right)} \left( {r,T} \right) , $$

(1)

where right-hand side is the sum of the heat of formation, ΔE ⁽ⁿ⁾_el (r), lattice vibration energy, ΔE ⁽ⁿ⁾_vib (r, T), and vibration entropy, ΔS ⁽ⁿ⁾_vib (r, T). Among these three terms, heats of formation, ΔE ⁽ⁿ⁾_el (r), are calculated by the spin-polarized FLAPW method as a function of lattice constant, r (or equivalently nearest neighbor atomic distance for a cubic crystal). The lattice-vibration effects are evaluated based on the Debye-Grüneisen theory within the quasi-harmonic approximation.[10] The procedure of calculating the vibrational contributions has been amply demonstrated in previous articles[5–9,11,12] and the reader interested in the procedure should consult them. The binding energy curve which is equivalent to the heat of formation curve for each phase n provides with the bulk modulus, Debye temperature and Grüneisen constant, and based on this information, vibrational energy and entropy are derived in a straightforward manner.

The particular phases studied in the present investigation are five fcc-based structures, namely, Fe (n = 1), Fe₃Pt (n = 2) with L1₂, FePt (n = 3) with L1₀, FePt₃ (n = 4) with L1₂ and Pt (n = 5). In view of the fact that the most stable ground state of pure Fe is not fcc but bcc with ferromagnetic order, an additional calculation is performed on bcc Fe.

By following the procedure of the cluster expansion method (CEM),[13] the free energy of formation is expanded as

$$ \Updelta F^{\left( n \right)} \left( {r,T} \right) = \sum\limits_{m = 0} {v_{m} \left( {r,T} \right) \cdot \upxi_{m}^{n} } $$

(2)

where v _m (r, T) and ξ ⁿ _m are an effective cluster interaction energy and a correlation function,[14,15] respectively, for a cluster m. It is noted that a set of correlation functions {ξ ⁿ _m } forms an orthonormal basis in the thermodynamic configuration space. In general practice, the number of phases considered in the CEM is quite large, however in the present study a minimum set of meaningful phases, n = 1-5, are considered. Hence, the correlation functions {ξ ⁿ _m } form a 5 × 5 matrix and, therefore, the effective cluster interaction energies up to a four-body tetrahedron cluster are derived through,

$$ v_{m} \left( {r,T} \right) = \sum\limits_{n = 1}^{5} {\left\{ {\upxi_{m}^{n} } \right\}^{ - 1} \cdot \Updelta F^{\left( n \right)} \left( {r,T} \right)} $$

(3)

It is noted that the present CEM is performed on temperature-dependent heats of formation ΔF ⁽ⁿ⁾(r, T) which is defined with reference to the segregation limit at each temperature.

With the effective cluster interaction energies, the free energy of a disordered phase can be written as

$$ \Updelta F = \sum\limits_{m = 0}^{4} {v_{m} \left( {r,T} \right)} \cdot \upxi_{m} - T \cdot \Updelta S_{\text{Conf}} $$

(4)

where ΔS _Conf is a configurational entropy which can be most efficiently described by the CVM that constitutes a hierarchy structure in the level of approximation in terms of a basic cluster which is the biggest cluster considered in the entropy formula. In the present study, we employed the tetrahedron approximation[16] that is recognized as a minimum meaningful approximation in the CVM hierarchy for a fcc based structure given as

$$ \Updelta S_{\text{Conf}} = k_{\rm B} \cdot \ln \frac{{\left\{ {\prod\nolimits_{i,j} {\left( {Ny_{ij} } \right)!} } \right\}^{6} N!}}{{\left\{ {\prod\nolimits_{i} {\left( {Nx_{i} } \right)!} } \right\}^{5} \left\{ {\prod\nolimits_{i,j,k,l} {\left( {Nw_{ijkl} } \right)!} } \right\}^{2} }} , $$

(5)

where i,j,… indicate either Fe or Pt, and x _i , y _ij and w _ijkl are cluster probabilities of finding atomic arrangement specified by subscript(s) on a point, pair and tetrahedron clusters, respectively.

By substituting Eq 5 into Eq 4, the free energy is written as

$$ \Updelta F = \sum\limits_{m = 0}^{4} {v_{m} \left( {r, T} \right) \upxi_{m} - k_{\rm B} T\ln } \frac{{\left\{ {\prod\nolimits_{i,j} {\left( {Ny_{ij} } \right)!} } \right\}^{6} N!}}{{\left\{ {\prod\nolimits_{i} {\left( {Nx_{i} } \right)!} } \right\}^{5} \left\{ {\prod\nolimits_{i,j,k,l} {\left( {Nw_{ijkl}^{\alpha \alpha \beta \beta } } \right)!} } \right\}^{2} }} $$

(6)

It is noted that the free energy formula given above is for a disordered phase, but the extension to an L1₀ ordered phase is quite straightforward by distinguishing two kinds of sub-lattices in the L1₀ ordered phase.

In Eq 6, the correlation functions {ξ _m } and cluster probabilities, {x _i , y _ij ,…, w _ijkl }, are mutually interrelated through a linear transformation.[14,15] Hence, the free energy is formally written as ΔF(v _m (r, T), {ξ _m }) and an equilibrium state at a given temperature T is determined by minimizing the free energy with respect to a set of correlation functions {ξ _m } and an atomic distance r,

$$ \left. {\frac{\partial \Updelta F}{{\partial \left\{ {\upxi_{i} } \right\}}}} \right|_{{T,\left\{ {\upxi_{j \ne 1} } \right\},r}} = 0 $$

(7)

and

$$ \left. {\frac{\partial \Updelta F}{\partial r}} \right|_{{T,\left\{ {\upxi_{i \ne 1} } \right\}}} = 0 $$

(8)

It is pointed out that the actual minimization of the free energy is carried out after performing the Legendre transformation on ΔF(v _m (r, T), {ξ _m }) to derive a grand potential in which the point correlation function is replaced by the effective chemical potential.

Spinodal Ordering and Short Range Order Diffuse Intensity Scattering Spectrum

In general, the second-order derivative of the free energy, ΔF(φ), with respect to an independent variable φ represents the stability of the system against fluctuation of the variable φ. If the variable φ is a concentration c, this is nothing but the criterion of spinodal decomposition for which the homogeneous solid solution becomes unstable against concentration fluctuation and decomposes into two phases. While, in the case of ordering system, φ is a configurational variable such as a correlation function, ξ _m , as described in the previous section. And the physical meaning of the stability is posed as the ordering instability, indicating that the fluctuation of the configurational variable in a disordered solid solution leads to the ordering reaction. Since theoretical details have been amply described in previous articles,[3,4,17,18] only essential points are reproduced here.

As seen in the previous section, the CVM free energy generally contains multi configurational variables and, therefore, it is mathematically convenient to discuss the second-order derivative of the free energy in k-space by performing a Fourier transformation.

It is noted that Δ of ΔF(v _m (r, T), {ξ _m }) indicates the free energy of formation with reference to the segregation limit, however in order to simplify the notation Δ is omitted to denote F(v _m (r, T), {ξ _m }) and each correlation function is regarded as a fluctuating variable φ. Then, the deviation of the free energy from a homogeneous state F ₀ is written as

$$ \updelta F = F - F_{0} \cong \frac{1}{2}\sum\limits_{l,l'} {\sum\limits_{p,p'} {\frac{{\partial^{2} F}}{{\partial \upxi_{i} \cdot \partial \upxi_{j} }}\Updelta \upxi_{i} \left( p \right) \cdot \Updelta \upxi_{j} \left( {p^{\prime}} \right)} } $$

(9)

where p and p′ indicate lattice sites, Δξ _i (p) is the deviation of ith correlation function at a lattice point p from the homogeneous state. By making use of the translational symmetry of the homogeneous solid solution, one can perform the Fourier transformation on Eq 9 to yield

$$ {\text{FT}}\left( {\updelta F} \right) = \frac{1}{2}\sum\limits_{{l,l^{\prime}}} {\sum\limits_{{\mathbf{k}}} {f_{{ll^{\prime}}} \left( {\mathbf{k}} \right) \cdot \Updelta X_{l}^{*} \left( {\mathbf{k}} \right) \cdot \Updelta X_{{l^{\prime}}} ({\mathbf{k}})} } $$

(10)

where FT indicates a Fourier transformation, $\Updelta X_{l} \left( {\mathbf{k}} \right)$ is defined as $\Updelta X_{l} \left( {\mathbf{k}} \right) = \sum\nolimits_{{\mathbf{p}}} {\Updelta \upxi_{l} \left( {\mathbf{p}} \right)} \cdot \exp \left( { - i{\mathbf{k}} \cdot {\mathbf{p}}} \right)$ and $\Updelta X_{l}^{*} \left( {\mathbf{k}} \right)$ is a conjugate variable of $\Updelta X_{l} \left( {\mathbf{k}} \right)$. By noting that the second order derivative matrix $f_{{ll^{\prime}}} \left( {\mathbf{k}} \right)$ is a Hermitean matrix, one can diagonalize the matrix to derive the eigenvalues,

$$ {\text{FT}}\left( {\updelta F} \right) = \sum\limits_{l} {\sum\limits_{{\mathbf{k}}} {\Uplambda_{l} } } \left( {\mathbf{k}} \right) \cdot \left| {\Updelta Z_{l} \left( {\mathbf{k}} \right)} \right|^{2} $$

(11)

where $\Uplambda_{l} ({\mathbf{k}})$ and $\left| {\Updelta Z_{l} \left( {\mathbf{k}} \right)} \right|$ are, respectively, the lth eigenvalue and the normal-mode amplitude. It is noted that in the case of an homogeneous solid solution at a high temperature all the eigen values are positive, while as the temperature is lowered and as soon as one of the eigen values goes through zero, the system becomes inherently unstable against the excitation of a particular wave k ₀ associated with the negative eigen value.

Then, the limit of the stability of an homogenous solid solution against the configurational fluctuation is formally given as the vanishing condition of the determinant of the second-order derivative of the free energy matrix associated with the zero of a specific eigenvalue,

$$ \det f_{{ll^{\prime}}} \left( {T_{s} ,{\mathbf{k}}_{0} ,C} \right) = 0 , $$

(12)

and the highest temperature at which this condition is satisfied is defined as the spinodal ordering temperature, T _s.

Finally, it has been amply discussed[3,4,17,18] that since the diffuse intensity spectrum, I(k), in k-space is given by

$$ I\left( {\mathbf{k}} \right) = \frac{{k_{\text{B}} \cdot T}}{N}f_{11}^{ - 1} \left( {\mathbf{k}} \right) $$

(13)

where N is the total number of lattice points in the system, one can readily understand that the diffuse intensity at k ₀ becomes unbounded as approaching the spinodal ordering temperature T _s.

Results and Discussion

The calculated disorder-L1₀ phase diagram is reproduced in Fig. 1[5] by solid lines. The transition temperature reported by experiment is about 1600 K at 50 at.% while our first-principles calculation yields 1610 K which is in good agreement with the experimental value. It is noted that the temperature dependent heats of formation ΔF ⁽ⁿ⁾(r, T) in Eq 2 and 3 are derived by including vibrational free energy contribution evaluated through Debye-Grüneisen model for each phase n in addition to the electric contribution. Without vibrational energy contribution, the disordered phase is understabilized and order-disorder transition temperature is overestimated.[5] The temperature dependence of long-range-order parameter at 50 at.% in Fig. 2 confirms that the L1₀-disorder transition is of the first order.

Fig. 1

Disorder-L1₀ phase boundary (diamond symbols linked by solid lines)[5] and spinodal-ordering temperature (dots) for the Fe-Pt system

Fig. 2

Temperature dependence of long-range-order parameter at 50 at.%

The calculated SRO diffuse-intensity spectra on (001) plane in k-space are shown in Fig. 3(a) and (b) at 50 at.% at two temperatures, 3000 and 1650 K. One sees that the intensity distribution becomes sharper with decreasing the temperature and that the diffuse-intensity maxima appears from (1,0,0) towards (1,1/2,0) along 〈010〉 in both cases. In fact, (1,0,0) and (1,1/2,0) are two of four special points which are closely related to underlying ordered phases in the fcc structure. These special point family and corresponding ordered phases have been discussed based on symmetry of the lattice and are displayed in Fig. 4.[17] The vertical axis indicates the ratio, α, of the second (v _2,2) to the first (v _2,1) nearest neighbor effective pair interaction energies with v _2,1 > 0, and the stable ordered phases at 50 at.% found by the ground state analysis[19,20] are displayed together with the corresponding special points. The fact that the intensities at the two special point positions are identical in Fig. 3(a) and (b) indicates the degeneracy of the stability of the two corresponding phases, L1₀ for 〈100〉 and Chalcopyrite for 〈1 1/2 0〉. In fact, these two phases are energetically degenerated at the ground state within the nearest neighbor pair interaction as shown in Fig. 4 (α = 0). In order to lift the degeneracy, one needs to include the second nearest neighbor pair interaction energy and the entropy should be formulated based on the tetrahedron-octahedron approximation of the CVM.[14,15] This is beyond the scope of the present study, however we attempted subsidiary calculations to obtain second nearest neighbor pair interaction energy by a larger set of ordered phases in Eq 3. The effective interaction energies at 0 K are shown in Fig. 5. One sees that the first nearest neighbor pair interaction energy is positive and the second nearest neighbor pair interaction energy is negative at a lattice constant corresponding to 50 at.% as indicated by a vertical broken line, which confirms the stability of L1₀ ordered phase as shown in Fig. 4. However, the magnitude of v _2,2 is quite small and one may not expect a drastic change of the intensity distribution even if v _2,2 is included in the analysis.

Fig. 3

Short-range-order diffuse-intensity spectra at 3000 K (a) and 1650 K (b) in (001) plane in k-space at 50 at.%

Fig. 4

Most stable ground-state phases and corresponding special-point ordering waves for fcc-based systems at 1:1 stoichiometry as a function of second (v _2,2) to the first (v _2,1) nearest neighbor pair-interaction energies

Fig. 5

Effective cluster-interaction energies as a function of lattice constant up to a tetrahedron cluster and second nearest neighbor pair. The vertical broken line indicates the lattice constant at 50 at.% at 0 K

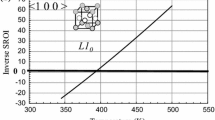
Shown in Fig. 6(a)-(c) are the plots of the $\left( {I\left( {\mathbf{k}} \right)T} \right)^{ - 1}$ vs. T for the four kinds of k vectors corresponding to special points. SRO diffuse-intensity is abbreviated as SROI on the vertical axis. One can see that the 〈100〉 and 〈1 1/2 0〉 waves fall off towards zero (intensity I(k) blows up) quickly as the temperature is lowered, see Fig. 6(a). This indicates that the stability of the system is lost against the excitation of 〈100〉 and 〈11/20〉 ordering waves and the system decomposes into underlying superlattice structure at T _s = 1400 K at which $\left( {I\left( {\mathbf{k}} \right)T} \right)^{ - 1}$ becomes zero. The other waves 〈1/2 1/2 1/2〉 and 〈000〉 decay as the temperature is lowered towards T _s. In view of the facts that the 〈100〉 ordering wave represents the L1₀ ordered structure and the degeneracy is lifted in favor of the L1₀ ordered phase when the second nearest neighbor pair interaction energy is included, only 〈100〉 stability is considered in the following.

Fig. 6

(I(k) T)⁻¹ vs. T for four kinds of special point positions in k-space. See Fig. 4. 〈000〉 Indicates phase separation

Similar calculations are performed at other alloy compositions to determine the locus of the spinodal ordering temperature[1] as shown by a dotted line in the phase diagram in Fig. 1. The physical significance of the spinodal ordering temperature is as follows. In the temperature range between the spinodal ordering temperature and the phase boundary, disorder-L1₀ ordering takes place by nucleation-growth mechanism while below the spinodal ordering temperature L1₀ is formed spontaneously by the excitation, amplification and propagation of 〈100〉 ordering wave. Hence, the separation of the two temperatures represented by the spinodal ordering locus and phase boundary is a measure of the magnitude of the first and second order natures of the transition. When the two temperatures coincide, the transition is of the second order, while the more the two temperatures are separated the more the first order nature is emphasized. In fact, the abrupt change of the long range order (LRO) parameter near the transition temperature shown in Fig. 2 agrees with this result.

In the present study, starting from a single free energy formula, we derived a phase diagram, spinodal-ordering temperature and short-range-order diffuse-intensity spectrum for disorder-L1₀ transition of the Fe-Pt system. The transition temperature agrees with the experimental one with high accuracy, the depth of the spinodal-ordering temperature with reference to the transition temperature confirms the first-order nature of the transition and the short-range-order diffuse-intensity spectrum produces the intensity maximum at the correct position in k-space. All these results indicate the reliability and accuracy of the CVM-based free energy. It is claimed that the second-order derivative of the free energy provides with affluent information associated with phase equilibria, and that the reliability of the free energy employed for phase equilibria calculations should be examined not only by the agreement/disagreement of the phase boundaries but also by the consistencies among transition and spinodal-ordering temperatures and short-range-order diffuse intensities.