Abstract
This work presents a primer on “How to Read and Apply Phase Diagrams” in the current environment of powerful thermodynamic software packages. Advanced aspects in that context are also covered. It is a brief guide into using this cornerstone of knowledge in materials science and engineering and offers assistance in the proper interpretation of results obtained from state-of-the-art Calphad-type thermodynamic calculations. Starting from the very basics it explains the reading of unary, binary and ternary phase diagrams, including liquidus projections, isothermal and vertical phase diagram sections. Application examples are directly derived from these phase diagrams of Fe, Cu-Ni, Mg-Al, and Mg-Al-Zn. The use of stable and metastable phase diagrams and appropriate choices of state variables are explained for the relevant Fe-C and Fe-C-Si systems. The most useful concept of zero-phase fraction lines in phase diagram sections of multicomponent systems is made clear by coming back to the Cu-Ni and Mg-Al-Zn systems. Thermodynamic solidification simulation using the Scheil approximation in comparison to the equilibrium case is covered in context of multicomponent multiphase solidification and exemplified for Mg-Al-Zn alloys. The generic approach is directly applicable for all inorganic materials, but exemplified in this concise work for a small selection of metallic systems to highlight the interdependences among the phase diagrams. The embedded application examples for real material systems and various materials processes also emphasize the use of phase diagrams for the path from initial off-equilibrium state towards equilibrium.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
“Phase diagrams are the beginning of wisdom-not the end of it”. This famous quotation coined by Sir William Hume-Rothery is a perfect guideline for any work in materials science and technology. Virtually all materials of practical interest are composed of various phases. Each phase is an essentially homogeneous part of the system with definite bounding surfaces (phase boundaries) and unique “structure”, such as gas, liquid, or one of the many solid crystal structures. All of the physical and chemical properties of a material are basically governed by the type of phase(s) and, in a multiphase material, the phase assembly.
Phase diagrams are the perfect road map to understand the conditions for phase formation or transformation in any material system caused by variation of temperature, composition, pressure or any other viable state variable. That is why one can use phase diagrams as the starting point for materials design and process optimization by manipulating composition and processing variables to achieve the desired microstructures. That applies to all sorts of materials, such as alloys, ceramics, semiconductors, cement, concrete etc., and to a multitude of processes, such as melting, casting, crystal growth, joining, solid-state reaction, heat treatment/phase transformation, oxidation, vapor deposition, and so on.
Properly constructed phase diagrams display the phase relations at thermodynamic equilibrium state of matter. That makes them unique for a given material system. On the other hand, they do not include kinetic effects, for instance the nucleation undercooling and/or growth undercooling observed in practical solidification. However, it is emphasized that phase diagrams are also indispensable to understand off-equilibrium processes. That is exemplified in this work for metastable phase diagrams and processes such as friction stir welding, coating, and non-equilibrium “Scheil solidification”.
The purpose of this work is to present a primer on “How to Read and Apply Phase Diagrams” in the current environment of powerful software packages. However, advanced aspects in that context will also be covered. It aims at a readership with no or insufficient prior exposure to phase diagrams or chemical thermodynamics. The intention is also to guide those with a different background, such as mechanical engineering, physics or chemistry, into using this cornerstone of knowledge in materials science and engineering.
Starting from the very basics of phase diagrams and phase equilibria we will go through reading unary, binary and ternary phase diagrams, including liquidus projections, isothermal and vertical phase diagram sections. Application examples are directly derived from these phase diagrams of Fe, Cu-Ni, Mg-Al, and Mg-Al-Zn. The use of stable and metastable phase diagrams and appropriate choices of state variables are explained for the relevant Fe-C system. The most useful zero-phase fraction lines in phase diagram sections of multicomponent systems are made clear by coming back to the Cu-Ni and Mg-Al-Zn systems. Finally, thermodynamic solidification simulation using the Scheil approximation in comparison to the equilibrium case is covered in context of multicomponent multiphase solidification. In many of the embedded application examples, explicitly demonstrated on real material systems and various materials processes, the path from initial off-equilibrium state towards equilibrium is emphasized.
Further reading is recommended in the classical textbook of Rhines,[1] for details on the thermodynamic basis of phase diagrams and phase transformations in Hillert’s textbook[2] or in the work of Chang et al.[3] Another example of applications of phase diagrams is given in the field of soldering and brazing in chapter 3 of Humpston and Jacobson’s book,[4] just to give a small selection.
This work is written in the context of state-of-the-art thermodynamic software packages for phase diagram calculation, such as Pandat,[5] Thermocalc[6] or Factsage,[7] which are all based on the Calphad method.[8] The intention is to assist in the proper interpretation of results obtained from such calculations, not in the operation of such calculations. In fact, all diagrams presented in this work are produced by thermodynamic calculations using the Pandat software package[5] and the quantitative thermodynamic database for Mg-alloys, PanMg,[9] unless noted differently. The examples shown are for metallic systems and related alloys, just to keep this work concise. The basic approach outlined here is directly applicable for all inorganic materials, as indicated above. Examples of binary phase diagrams are found even for organic[10] and polymeric[11] materials, however, not as widespread as for inorganic materials. The only condition for the applicability of phase diagrams as a powerful tool in materials science and engineering is that the concept of phase, as defined above, is viable for the material under consideration.
Property Diagram Versus Phase Diagram
Pure Iron
The most important distinction in this field is the one between property diagram and phase diagram. Figure 1 shows the enthalpy of pure iron as function of temperature at constant pressure of 1 bar. It is a property diagram; the areas in that diagram have no meaning. Only the curve has a meaning. It is labeled with the different phases associated with the three different continuous parts of the enthalpy curve, BCC (α), FCC (γ), and BCC (δ), where BCC and FCC are a shorthand for the different crystal structures, body centered cubic and face centered cubic, respectively. Figure 1 is not a phase diagram.
Figure 2 shows the phase diagram of pure iron. This is a unary system, build from a single component. The axes are the state variables, temperature T and pressure P, the pressure is shown in log-scale to reveal the gas phase region together with the high-pressure part. All of the areas in that diagram have a meaning as seen from the following example. Consider the state point at 1000 K and 103 bar, indicated by the crosshairs in Fig. 2. That is, we put a certain amount of pure Fe in a closed box and fix the temperature and pressure at these values. Now the Fe atoms may arrange themselves in various phases, such as Gas, Liquid, BCC, FCC, or HCP. Each phase has a unique value of Gibbs energy, G phase (T, P), at that given state point. The phase with the lowest value of Gibbs energy G is the “winner”; it is the stable phase under the given condition. In this case, it is the BCC (α) phase. In fact, the outcome of competition among phases in the entire region bounded by the boundary lines between BCC (α)/FCC (γ) and BCC (α)/HCP is the same, i.e., BCC (α) wins. In other words, this is the stable single-phase region of BCC (α) phase, and at any state point in this region the Gibbs energy value of any competing phase is higher than that of the BCC (α) phase. The same competition rule applies to all state points in the entire phase diagram in Fig. 2 which composes of the single phase regions of Gas, Liquid, BCC (δ), FCC (γ), BCC (α), and HCP. If one chooses to use other state variables different from T and P, other thermodynamic functions instead of Gibbs energy must be minimized to find the stable field of each phase. This aspect will not be further discussed here.
The boundary line between the BCC (α) and FCC regions is defined by the equality of the Gibbs energy values, G BCC (T, P) = G FCC (T, P). That line not only reveals the pressure dependence of the BCC (α)/FCC phase transformation temperature, but also forms the two-phase region BCC (α) + FCC in the phase diagram. All these two-phase regions in Fig. 2 are one-dimensional lines because of the choice of state variables, T and P, for plotting this diagram. The three-phase region BCC (α) + FCC + HCP occurs only at a unique state point, 757 K and 105.019 bar, in the phase diagram. Therefore, this is an invariant equilibrium, also called a triple point. The degrees of freedom are zero at an invariant equilibrium according to the Gibbs phase rule. That means one cannot change any state variable (T or P) without loosing a phase from the equilibrium. By contrast, the two-phase equilibrium BCC (α) + FCC in Fig. 2 is monovariant, it has one degree of freedom. One variable may be changed, at least infinitesimally, and by adjusting the other one along the T–P relating line the BCC (α) + FCC equilibrium may be maintained. When plotting the phase diagrams with the choice of different state variables as axes (e.g. enthalpy instead of temperature) the topology of the two- and three-phase regions may change so that they are no longer one- or zero-dimensional, as will be discussed later.
The geological relevance of the phase diagram of iron is that it helps explaining why the inner core of our earth is solid. That is peculiar because the temperature increases all the way down to the earth’s center so that the outer core, composed mainly of an iron-nickel alloy, is liquid. However, going further down, the alloy solidifies at the boundary to the inner core, even though the temperature still increases. That is because of the monotonous pressure increase, resulting in a dramatic increase of the melting temperature, shown for pure Fe in Fig. 2. The pressure at the boundary is about 330 GPa, or 3.3 × 106 bar, just outside the frame of Fig. 2, and the melting temperature of the Fe-rich alloy at this pressure is estimated to be 5600 K.[12] The additional pressure increase subsequently solidifies the alloy.
The industrial importance of steel basically originates from a peculiarity of the phase diagram in Fig. 2, the occurrence of two separate regions of BCC, one at high temperature BCC (δ), and one at low temperature, BCC (α). Normally the more densely packed FCC crystals should be stable down to room temperature. However, the less densely packed BCC iron crystals undergo magnetic ordering, which significantly decreases the values of G BCC (T), making the BCC phase stable again at lower temperature. That results in the occurrence of the γ/α phase transition of iron, which may be modified and tailored by addition of carbon and other alloying elements in steel. Properly designing this γ/α solid-state phase transition forms the basis for controlling the variety of microstructures in steel, from the as-cast structure through heat treatment or thermo-mechanical processing. Without the FCC (γ)/BCC (α) transition in Fig. 2 at ambient pressure man could not produce steel.
H2O and SiC
All other unary, or one-component, P-T phase diagrams can be understood following the example of iron. The rules and the resulting topology are identical if the component is an element or a pure substance, defined as a compound that cannot change composition. A prominent example is the phase diagram of pure H2O, shown in many textbooks with the phase regions of vapor, water, ice and, at high pressure, the various crystalline ice phases. However, it is quite a special case because all the phase transitions of H2O (e.g. melting, evaporation) are congruent ones, where at any two-phase equilibrium the compositions of both phases are identical. That is clearly fulfilled for all phases of H2O.
There are many other solid stoichiometric compounds with negligible solid solution range, or negligible stoichiometry deviation, forming a pure solid substance. Upon melting, however, the composition is often not maintained. That is for instance the case for silicon carbide, SiC, an important compound semiconductor and also an important hard ceramic material. Heating SiC at 1 bar above 2823 °C[13] produces a silicon-rich liquid phase with only 17 at.% C and in addition a certain amount of graphite, thus balancing the original 50 at.% C of SiC. That is, the single phase SiC crystal decomposes into a liquid and graphite, also called incongruent melting. That is a three-phase equilibrium, not simple two-phase melting. In the P-T phase diagram of SiC at 1 bar the single-phase region of solid SiC ends at 2823 °C, beyond a gap forms, the two-phase region liquid + graphite. Calculation with the database PanMg[9] shows that a temperature of 3600 °C (and pressure of at least 8 bar to avoid evaporation) is necessary to obtain single-phase liquid “SiC” with 50 at.% C. This 777 K wide gap, liquid + graphite, in the “P-T phase diagram of SiC” occurs because, technically speaking, it is a section in the P-T-x phase diagram of the binary Si-C system at constant 50 at.% C. Such phase diagram sections may exhibit phase compositions which are off the section plane as will be discussed in more detail later; they are also known as isopleths.
Therefore, the compound SiC does not form a unary P-T phase diagram, in contrast to the compound H2O. In order for the simple topology of Fig. 1, observed for any element, to prevail also for a compound it is necessary that this compound exists in all phases under all conditions (at all state points) as stable single phase, making all phase transitions congruent. Otherwise the topology of the P-T phase diagram will be more complex. The important distinction between property and phase diagram, however, is generally valid and must be kept in mind also for multicomponent systems.
Binary Phase Diagrams
Cu-Ni Phase Diagram
Figure 3 shows the phase diagram of the binary system Cu-Ni. The entire diagram is valid for a constant total pressure of 1 bar. Consider the state point indicated by the crosshairs in Fig. 3 at 1200 °C and composition x Ni = 80 at.% Ni. The mole fraction of Ni in the system, x Ni, may be written as x Ni = 0.80 or x Ni = 80 % in the “atomic percent of Ni”, at.% Ni, composition scale. That is, we put 0.20 mol of Cu atoms and 0.80 mol of Ni atoms in a closed box. One may choose any number of moles of atoms of that fixed composition instead of 1 mol, phase diagrams are independent of total amount. In addition we fix T = 1200 °C and P = 1 bar in the box. At that particular state point (T, P, x Ni) the Cu and Ni atoms may arrange themselves in various phases, such as Liquid, FCC, Gas, or in a combination of phases. Just like in the unary example the thermodynamic equilibrium requires G system (T, P, x Ni) = minimum. At that state point the minimum is attained if all atoms are in the FCC phase, thus G system (T, P, x Ni) = G FCC (T, P, x Ni). In the following the pressure condition P = 1 bar is not shown explicitly, also because the equilibrium temperatures among condensed phases (Liquid, Solid), in contrast to the gas phase, are almost independent of pressure up to about 100 bar as exemplified for iron in Fig. 2.
Phase diagram of the binary Cu-Ni system. The pressure is fixed at a value of 1 bar. Two state points are marked,  (80 at.% Ni, 1200 °C) and
(80 at.% Ni, 1200 °C) and  (60 at.% Ni, 1320 °C); one tie line, L + FCC, is marked by the symbol
(60 at.% Ni, 1320 °C); one tie line, L + FCC, is marked by the symbol  , where dots indicate the phase compositions of L (52.6 at.% Ni) and FCC (65.6 at.% Ni) at 1320 °C
, where dots indicate the phase compositions of L (52.6 at.% Ni) and FCC (65.6 at.% Ni) at 1320 °C
The FCC phase is a substitutional solid solution, the Cu and Ni atoms may substitute each other completely in the crystal structure. That is a necessary requirement for the formation of a complete solid solution range between the pure components. Because the absolute minimum of G system (T = 1200 °C, x Ni = 0.8) is found if all atoms are in the FCC phase, the state point at the crosshairs in Fig. 3 presents the stable single-phase constitution of FCC. The same result, G system (T, x Ni) = G FCC (T, x Ni) = minimum (with different numerical values), is obtained at any state point within the contiguous region labeled as FCC. Therefore, in the case of Cu and Ni, a complete single-phase region of the solid solution phase FCC is formed below the solidus line, and contiguous liquid forms above the liquidus line as shown in Fig. 3. In that single-phase Liquid region the absolute minimum of G system (T, x Ni) = G Liquid (T, x Ni) is attained by putting all atoms in the liquid solution phase.
For the state point indicated by the second crosshairs in Fig. 3 at 1320 °C and x Ni = 60 at.% Ni the equilibrium condition is also G system (T, x Ni) = minimum. It is emphasized that at each state point the variables (T, x Ni) are kept constant, thus, the only way to change the function value of G system (T, x Ni) in pursuit of the minimum is by smart distribution of atoms on various phases. At that state point let us try to put all atoms in either the Liquid or the FCC phase:
One might think that FCC with its lower, more negative, value of G is stable. However, an even lower value of G system is achieved if one part of the atoms is distributed on a Ni-poor Liquid phase and the rest on a Ni-rich FCC phase. Under the constraint of materials balance 0.428 mol of Liquid with 52.6 at.% Ni and 0.572 mol of FCC with 65.6 at.% Ni may form, maintaining the overall 60 at.% Ni of the system. For the individual phases we get
The total Gibbs energy of this two-phase system at 1320 °C with overall 60 at.% Ni and total amount of 1 mol of atoms equals the sum of the Gibbs energies of all present phases multiplied by their phase amount:
Comparing Eq 1, 2 and 5, these three alternative distributions of atoms result in three different values of G system (60 at.% Ni):
Therefore this two-phase mixture is more stable than any of the single phases. Moreover, the compositions of the Liquid and FCC phases have been selected in that example exactly so that no other distribution of atoms on the available phases produces a lower value of G system as given in Eq 5. That is the global minimum of the Gibbs energy of the system at this state point; this defines the stable two-phase equilibrium Liquid + FCC. That example demonstrates why we must have a “composition gap” in the two-phase region Liquid + FCC, also known as heterogeneous region.
For any state point within the contiguous region labeled as Liquid + FCC the same result, G system (T, x Ni) = G Liquid+FCC = minimum (with different numerical values), is obtained by smart distribution of atoms on the two phases. The resulting phase compositions are plotted as the phase boundaries Liquid/(Liquid + FCC), the liquidus line, and FCC/(Liquid + FCC), the solidus line, in Fig. 3. At any state point in the Liquid + FCC region they can be read from the tie line joining the two equilibrium phase compositions, as plotted for the example of the state point at 1320 °C and 60 at.% Ni with Liquid at 52.6 at.% Ni and FCC at 65.6 at.% Ni. The tie line is horizontal because the two phases must of course be at the same temperature to be in equilibrium. Any two-phase region in a binary temperature-composition phase diagram follows these same rules.
In addition the phase fractions may be easily calculated by the lever rule, derived from the materials balance. The closer the state point is located to one end of the tie line the larger the fraction of this phase is. In our example the phase fractions, f phase, are calculated from the compositions of system and phases as follows:
with f FCC + f Liquid = 1. Note that these dimensionless fractions carry a hidden unit, mol/mol, because the composition scale in Fig. 3 is in at.%. If we had used the mass% (or wt.%) scale the calculation for the same alloy results in f FCC = 0.569 and f Liquid = 0.431 with the hidden unit of g/g. Therefore it is necessary to specify if “mass fraction of phases” or “atomic fraction of phases” are reported.
Phase Diagram Applications Exemplified with Cu-Ni
For a simple application to solidification under strict equilibrium conditions we may consider an alloy with fixed composition of 52.6 at.% Ni which is completely molten at 1400 °C and then slowly cooled. At 1320 °C the liquidus point of this alloy is encountered and the first small crystal of composition 65.6 at.% Ni may form. Upon further cooling both the Liquid and FCC compositions become more Cu-rich. That may be envisaged by a sequence of tie lines while the state point (at constant 52.6 at.% Ni) moves down from 1320 to 1271 °C where it hits the phase boundary FCC/(Liquid + FCC) at the solidus point. At this last tie line the last droplet of liquid has attained 37.9 at.% Ni and the composition of FCC equals the 52.6 at.% Ni of the alloy. The equilibrium solidification is thus terminated and further cooling occurs in the single-phase FCC region. It is emphasized that, generally, there is no such thing as a “melting point” of an alloy but a melting interval between solidus and liquidus with ΔT = 49 K in this example. The significant composition variation of 52.6-37.9 at.% Ni in Liquid and 65.6-52.6 at.% Ni in solid FCC during “equilibrium” solidification requires sufficiently fast diffusion to attain complete equilibrium in all parts of the alloy, especially in the solid. It will be discussed later how to relieve this constraint using the Scheil simulation.
Another very useful application of the phase diagram is materials compatibility and materials bonding. Assume we drop a piece of solid nickel, preheated to 1320 °C, into pure liquid copper kept in a furnace at constant 1320 °C. In a first step we plot the initial status of materials into Fig. 3, one point at pure Cu the other at pure Ni, both at 1320 °C. The phase diagram tells us that there is no tie line between these points, thus, there is no equilibrium and therefore a reaction is expected. In a second step we calculate or estimate the overall composition of this (closed) system. Assume the piece of nickel is small, amounting to only 10 at.% Ni in our Cu-Ni experiment. This defines the state point at 1320 °C and 10 at.% Ni, which is in the single-phase liquid region in Fig. 3. That is the direction into which the reaction between the initial materials is expected to go and also the final state of the system; the solid piece of Ni will completely dissolve in the melt.
If our experiment is performed the other way around, pouring liquid copper in a nickel crucible at 1320 °C, the first two steps in applying the phase diagram are done in the same way. If we have a thin Ni crucible, amounting to a total of 10 at.% Ni in the system (as before), the dissolution will produce a hole in the crucible and a mess in the furnace. With a thick Ni crucible and, say, total 85 at.% Ni of the system, that state point is in the single-phase FCC region in Fig. 3. Now, in a third step, we use this knowledge to assess a realistic reaction path. Ni from the crucible will dissolve in the liquid Cu, shifting its composition towards the liquidus point. Concurrently, some Cu will dissolve in the FCC-Ni, shifting its composition in the direction of the solidus point, in a much slower solid state diffusion process. During that process the amount of liquid decreases because Cu is taken out of the liquid. A composition gradient builds up in the crucible, and at the Liquid/FCC interface a local equilibrium is attained with the composition of the two phases given by the tie line in Fig. 3. Eventually, the amount of liquid goes to zero, with the last drop of liquid at 52.6 at.% Ni and the FCC at 65.6 at.% Ni at the last contact point. Now the system is isothermally solidified. The composition gradient in the single-phase (not yet homogeneous!) FCC crucible is eventually leveled out by solid state diffusion until the equilibrium dictated by the state point at 85 at.% Ni and 1320 °C is attained in the homogeneous FCC.
Exactly that process is widely used in transient liquid phase bonding (TLP) or diffusion brazing.[4,14] In our example a thin Cu foil would be clamped between two relatively thicker Ni plates. This assembly is heated above the melting point of Cu but much below that of Ni so that the state point of the assembly is in the single-phase FCC region. At constant bonding temperature, just above 1085 °C, a solid bond is formed, which is even stable at much higher temperature, up to 1397 °C, the solidus point in our example of 85 at.% Ni system composition. That process is applied in many material systems where at least the part around the substrate is similar to the Ni-rich region in Fig. 3 with significant solid solubility, a low melting filler material and no intermetallic phases occurring at the bonding temperature. No intermetallic phases are formed in the bond during the diffusion brazing process in contrast to soldering or diffusion soldering[15–17] which is ruled by different phase diagrams.
Mg-Al Phase Diagram
The Mg-Al phase diagram is shown in Fig. 4 as an example for a system with formation of compounds, which are also called intermetallic phases if the components are metals as in this example. For the state point indicated by the crosshairs at 400 °C and composition 95 wt.% Al the equilibrium constitution is obviously the single-phase FCC solid solution. The state point at 63.59 wt.% Al and 100 °C is also in a single-phase “region”, namely the β phase region. However, this region appears degenerate to a line in the plot at constant 63.59 wt.% Al, thus, the β phase is also called a line compound. By contrast the single phase region of γ is so large it is easily discerned. Another name often used for the γ phase is Al12Mg17, however, the stoichiometry suggested by this name is only approximate and the phase diagram elucidates how the stoichiometry variation, or the stable solid solution range of γ, depends on temperature. Thermodynamics require that all compounds must have a finite solid solution range, but it may not be resolved on the plotted phase diagram as is the case for the phases β and ε in Fig. 4. All single-phase regions in Fig. 4 are marked by color shading, leaving all the two-phase regions blank.
The region where the three phases HCP + L + γ are in equilibrium at 436.3 °C is marked by the line, with dots indicating the phase compositions. This is the intersection of three two-phase equilibria, HCP + L, HCP + γ, and L + γ, which may also be seen as the overlap of these three tie lines. This three-phase equilibrium region is a true line (1D), while all the two-phase and single-phase regions are areas (2D), remembering that even the β and ε regions will extend under sufficiently high magnification. That is why the three-phase equilibrium is an invariant equilibrium, temperature and all phase compositions are fixed. All other three-phase equilibria in Fig. 4 follow the same rules.
This topological degeneracy of the invariant equilibrium to a phase region with lower dimension in the phase diagram is general. Look at the congruent melting point of γ at 463.4 °C and 48.8 wt.% Al, which is also an invariant equilibrium, L + γ, at a true point (0D) where the liquidus and solidus lines of γ touch at the maximum. On either side of that point the L + γ two-phase equilibrium extends into a normal 2D region and a melting interval. This is also seen in systems with more (or less) than two components. Consider for example pure Mg in Fig. 4. The single phase regions HCP and L are lines (1D) along the temperature axis, whereas the invariant two-phase region HCP + L is a point (0D), the melting point of magnesium.
If a state point is chosen in a three-phase region, for example at 20 wt.% Al and 436.3 °C in Fig. 4 we can read from the phase diagram that the three phases HCP, L, and γ occur in equilibrium with compositions at 12.7, 33.3, and 42.5 wt.% Al, respectively. However, the phase fractions are not fixed and the lever rule cannot be applied because this system composition is not on a unique tie line. This is also the case at the melting point of pure Mg where the phase fractions of HCP and L are not determined by just fixing the temperature because we cannot know if we are at the begin or the end of the melting process of that invariant equilibrium. That is generally the case for all invariant equilibria in this temperature-composition phase diagram: one can read only the type of phases and their composition but not the phase fractions. For any state point outside the invariant equilibrium regions one can read the complete constitution information: type of phases, composition of phases, and fraction of phases.
All invariant equilibria, or invariants, can be written as invariant reactions, for example L = HCP + γ. This is the so-called eutectic reaction, where L decomposes into the solid phases HCP and γ upon extraction of heat. In other words it is attempted to decrease the temperature of the alloy which is only possible in equilibrium once the liquid phase completely disappeared and the subsequent two-phase region HCP + γ is entered. The accepted notation is to always write the reaction in this direction of decreasing temperature.
Such a decomposition reaction is also observed for the three-phase equilibrium γ + ε + β at 250.1 °C, ε = γ + β. This is called a eutectoid reaction; the ending “oid” indicates that solid phases only are involved. It would be a eutectic reaction if ε is replaced by a liquid. The only other possible reaction type is the formation reaction, where two phases react to form a third one. This is seen for example at the other γ + ε + β three-phase equilibrium at 409.8 °C, γ + β = ε. This is called a peritectoid reaction. If one of the reactant phases were a liquid it would be called a peritectic reaction, not occurring in the Mg-Al system. It occurs in the Mg-Zr system where L + (Mg) + (Zr) form the invariant equilibrium at 653.6 °C with the peritectic reaction L + (Zr) = (Mg). The notation (Mg) is used here as an alternative to denote the HCP solid solution phase, similarly for (Zr). Mg and Zr (without the brackets) denote the components, not the solid phases. The peritectic reaction L + (Zr) = (Mg) occurs above the melting point of pure Mg (649.8 °C). That is because the solubility of Zr in solid (Mg) is larger than in the liquid, thus, the melting interval (Mg) + L develops to higher temperature with Zr addition as opposed to the case of Al addition in Fig. 4.
An important distinction between the decomposition and formation reaction type is in the kinetics. Generally, the formation reaction (peritectic/peritectoid), λ + φ = μ, slows itself down because the solid product phase μ produces a growing diffusion barrier between the reactant phases λ and φ. Therefore this reaction type is prone to not finish under real alloy cooling conditions and to leave unreacted, non-equilibrium remains. As opposed to that, the decomposition reaction (eutectic/eutectoid), λ = φ + μ, may occur much closer to the equilibrium phase diagram because there is no barrier phase formed. With higher cooling rates the microstructure of the growing φ + μ phases simply adjusts to a finer size with shorter diffusion distances.
When reading a phase diagram of the type in Fig. 4 a simple rule is helpful. If we cross a phase boundary we either gain a phase or loose a phase. Consider the path indicated by the dashed arrow for the Mg90Al10 (wt.%) alloy between 650 and 350 °C. We start in the single-phase liquid phase and the phase sequence is L/HCP + L/HCP/HCP + γ and the rule obviously holds. For the Mg80Al20 (wt.%) alloy between 600 and 350 °C the phase sequence is L/HCP + L/HCP + L + γ/HCP + γ. Highlighted by bold font is the eutectic three-phase region and the rule holds. This clarifies that the horizontal eutectic line is a phase region, not just a phase boundary. Otherwise we would read the wrong phase sequence L/HCP + L/HCP + γ, where the “gain a phase or loose a phase” rule is violated.
Phase Diagram Applications Exemplified with Mg-Al
One important application of thermodynamic software packages is the calculation of expected equilibrium phase fractions as function of temperature for a given alloy composition. That is shown for the Mg90Al10 (wt.%) example alloy in Fig. 5. In principle one could calculate that manually using the lever rule, see Eq 7-8, after plotting the tie lines at various temperatures in the phase diagram in Fig. 4. That is not only tedious but becomes difficult or impossible if the alloy contains more than two components. On the other hand the thermodynamic calculation is done rapidly for any number of components along the line of state points with fixed composition and variable temperature and an easy to read diagram similar to Fig. 5 is obtained. That is why this type of calculation is also called a line calculation, or a 1D (scan) calculation, or lever rule calculation. The result is not a phase diagram but a property diagram, such as in Fig. 5.
Reading in the direction of decreasing temperature the liquid fraction shrinks from 1 (liquidus point, 598 °C) to zero (solidus point, 472 °C), thus defining the freezing range, 126 K, of this alloy. Note that this is the equilibrium freezing range, which is a limiting case requiring complete equilibration in all parts of the alloy at each temperature step, as discussed above for the Cu47.4Ni52.6 alloy. Another useful limiting case, the Scheil simulation, will predict a wider freezing range for this alloy as discussed later. Concurrently with the shrinking amount of liquid the fraction of solid phase, only HCP for this case, grows from 0 to 1. Between 472 and 380 °C the single-phase region of solid HCP exists and this defines a potential solution heat treatment window for this alloy. This information is important because during non-equilibrium solidification, discussed later, some secondary phase may have formed in a coarse microstructure that should be dissolved during a solution heat treatment of that alloy. Subsequently an aging heat treatment may be performed to produce the second phase as fine precipitates in the HCP matrix during a solid state process. This is in principle possible for this alloy because below 380 °C the secondary phase γ forms at the expense of the HCP phase. That is also seen in the phase diagram from the retrograde solid solubility line (solvus line), the HCP/(HCP + γ) phase boundary. It is also seen that the solution heat treatment window widens for lower Al content of the alloy. For our Mg90Al10 example alloy the solution treatment must be performed below 472 °C to avoid partial melting and above 380 °C to form the single-phase HCP. Thereafter a relatively fast cooling down to room temperature will form a supersaturated solid solution (SSS) once the state point moves into the HCP + γ region, however, the nucleation and growth kinetics is too slow to produce the γ phase. In the subsequent aging treatment the SSS is heated to a point in the HCP + γ region with favorable kinetics, and held for example at 200 °C. Eventually the γ phase will precipitate and from tie line and lever rule at that state point a very large equilibrium mass fraction of f γ = 0.19 should finally form in the HCP matrix. These generic phase diagram features are essential for such processing steps and widely applied for microstructure design of alloys, even though our Mg90Al10 example alloy is not among the industrially used alloys.
The calculated molar phase fractions for the more Al-rich Mg80Al20 (wt.%) example alloy is shown in Fig. 6. The primary crystallizing phase is again HCP, starting to grow at the liquidus temperature of 539 °C, but then the secondary phase γ is formed in the eutectic reaction L = HCP + γ at 436.3 °C which terminates the solidification. The equilibrium freezing range of this alloy is 103 K. At the fixed eutectic temperature the liquid fraction drops from 0.35 to zero and simultaneously the solid fractions increase, from 0 to 0.24 for γ and from 0.65 to 0.76 for HCP. At this point the primary crystallized HCP and the eutectic HCP are exactly the same phase, both with 12.7 wt.% Al, however, they are distinguished in the microstructure of the solidified alloy. The primary HCP has grown freely in the melt, probably forming dendrites, whereas the eutectic HCP is found in finer microstructure, often lamellar, jointly with the γ phase. The fraction of eutectic HCP, 0.11 as dictated by the phase diagram, is therefore an important information. After completion of the invariant eutectic three-phase reaction the two-phase region HCP + γ is entered and Fig. 6 shows that the fraction of γ continues to grow at the expense of HCP. That is also seen in Fig. 4 because the solid solubility limits, the solvus lines, vary with temperature and for the given Mg80Al20 alloy the lever rule shows the same increasing fraction of γ. For a quantitative comparison one may calculate the mass fractions because the phase diagram is given in wt.%. However, in a micrograph the observed phase fraction are closer related to the volume fraction and quite often the molar phase fraction is a better approximate to that as compared to the mass phase fraction.
Ternary Phase Diagrams
Mg-Al-Zn Phase Diagram
Isothermal and Vertical Sections
In a ternary system, composed of three components, we select the state variables T, P, and composition. We assume constant total pressure, high enough to suppress any gas phase formation in all of the following. At constant temperature, say T = 500 °C, only two variables are left to fix the state point of the system. In the Mg-Al-Zn system we may select the contents of Al and Zn, thus fixing [wt.% Mg] = 100 − [wt.% Al] − [wt.% Zn]. The natural way to plot these two variables is in rectangular coordinates as shown in Fig. 7(a). Only the right-angle triangle area highlighted by the colored phase regions corresponds to real alloys; outside that range at least one composition becomes negative. The compositions on the straight line [wt.% Mg] = 0 are in the binary edge system Al-Zn. In order to obtain symmetry among the components the y-axis is tilted to get the equilateral or Gibbs triangle in Fig. 7(b), generally used if the complete composition range is covered. For enlargements of small composition ranges the rectangular diagram is much more useful, the tilted axis is disapproved for partial diagrams. Both figures are true phase diagrams because any point in the triangles corresponds to a fixed state point with unique constitution. That is shown for the intersection of the dotted lines for 30 wt.% Al and 20 wt.% Zn, where the single phase liquid is stable. At 500 °C in the Mg-Al-Zn system five single-phase regions are observed, L, HCP, FCC, τ, and MgZn2, the latter developing as a line compound due to significant solubility of Al in binary MgZn2. The term “line compound” refers to the one-dimensional extension of the single-phase region in the phase diagram section under consideration; it is also used for the phases β and ε in Fig. 4. A compound with no solubility range for any component is denoted as “stoichiometric compound”; the phase ε is an example that will be discussed in Fig. 8.
Coming back to the isothermal section of the Mg-Al-Zn phase diagram at 500 °C in Fig. 7, a number of two-phase regions, such as L + FCC, span between the solubility limits of single phases, marked by series of selected tie lines. For example, the tie line passing through the state point of the Mg10Al70Zn20 (wt.%) alloy indicates the compositions of the equilibrium phases L (50.2 wt.% Al, 33.4 wt.% Zn) and FCC (86.7 wt.% Al, 8.6 wt.% Zn). The lever rule can also be applied here, providing the mass fractions of the two phases, f Liquid = 0.458 and f FCC = 0.542. This is easily checked by the materials balance for Al, 50.2 × 0.458 + 86.7 × 0.542 = 70.0 wt.% Al, and analogously for Zn or Mg. Finally, two three-phase regions occur, marked by the red tie triangles. That completes the entire area of the phase diagram with unique constitution at each state point.
The isothermal section at 400 °C is shown in Fig. 8. At this lower temperature the extension of the single-phase liquid region shrinks into two separate patches and three more solid phases become stable, γ, ε, β, and Mg2Zn3. Note that the solid phases at 400 °C may be categorized as follows: HCP and FCC are terminal solid solutions, extending from the pure components; the Zn-rich HCP phase region is very small because we are just below the melting point of Zn at 419.5 °C. Another useful notation for these terminal solid phases is (Mg) and (Zn) for HCP and (Al) for FCC. We have two separate stable patches of the same phase HCP, just as we have two separate patches of L. Next we have γ, β, MgZn2, and Mg2Zn3, binary intermetallic phases with significant ternary solubility; only γ shows also a significant binary solution range, the other three appear as line compounds in the ternary. Next there is ε, a binary intermetallic phase that remains stoichiometric, visible only as a point on the Mg-Al binary edge. Finally there is τ, the only truly ternary solid phase since it does not connect in a continuous single-phase range to any of the binary edges, not even at different temperature. Another ternary solid phase, φ, will form below 387 °C.
Let us have a closer look at the three-phase region FCC + τ + β, marked by one of the red tie triangles in Fig. 8 with one apex at each of these single-phase boundaries. The state point of an example alloy Mg30Al50Zn20 (wt.%), marked by the crosshairs, is located inside this region, indicating that this combination of three phases is the most stable configuration of distribution of atoms on available phases with the absolute minimum of the Gibbs energy of the system. The composition of each phase is fixed and may be read at the corners of the tie triangle, FCC (88.6 wt.% Al, 1.6 wt.% Zn), τ (42.3 wt.% Al, 25.9 wt.% Zn), and β (55.9 wt.% Al, 10.2 wt.% Zn). The mass fractions are f FCC = 0.104, f τ = 0.681, and f β = 0.215, again determined by the lever rule. For any other alloy composition located inside this three-phase region FCC + τ + β the phase compositions remain fixed, only the phase fractions change. The closer the state point moves to a corner of this tie triangle the larger the fraction of this phase becomes.
One may envisage the complete ternary Mg-Al-Zn phase diagram (at constant pressure) as a prismatic 3D model, spanned by the triangular composition base and a vertical temperature axis. Each point inside that prism is a fixed state point with unique constitution: Type(s), composition(s), and fraction(s) of phase(s) are given by the equilibrium condition of Gibbs energy minimum. The isothermal sections in Fig. 7 and 8 form one way to produce a 2D section through the prism for quantitative display of the phase relations. The other way is the vertical section, also called T-x section or isopleth. If the interest is in phase relations along a series of alloys at various temperatures, the 3D prism will be sectioned parallel to the temperature axis along the composition line defined by the series of alloys. The result is a 2D section, such as in Fig. 9 for the example of ternary alloys at constant 20 wt.% Zn. The selected composition line along the alloy range Mg80Zn20-Al80Zn20 (wt.%) is also indicated by the dotted lines in Fig. 7 and 8. Along this line at 500 °C the same phase relations appear in Fig. 7 and 9. The stable regions of the liquid phase, or the FCC phase, are easily discerned in both diagrams.
The important distinction occurs in the two-phase region, such as L + FCC. Figure 7 clearly shows that for the alloy Mg10Al70Zn20 the phase compositions of L and FCC are off the section plane at constant 20 wt.% Zn, thus, the phase compositions cannot be read in Fig. 9. That is generally true for all two- or three-phase regions in a vertical section: Only the type of phases, not the composition of phases can be read from the vertical section. Therefore, the lever rule cannot be applied to determine the phase fractions. The complete constitution information can only be read from the isothermal section because all the tie lines are in the plane of that 2D section, and that is always the case for ternary systems.
In very rare and special cases all the tie lines may also happen to lie inside the plane of the vertical 2D section. In that case it is also necessary that the end points of the composition section are in a single-phase region, α or β, for example of a stoichiometric melting compound or a pure component. Not even that condition is met for the end point Mg80Zn20, that alloy is two-phase HCP + L. If all the tie lines are inside the plane this vertical phase diagram section between the phases α and β is called a pseudobinary system. It may be read like a binary system α-β, and it will provide the full constitution information on type, composition, and fraction of phases. Such pseudobinary systems are sometimes found in systems between stoichiometric oxides, such as Bi2O3-Fe2O3 in the Bi-Fe-O system,[18] or if a complete series of solid solutions exist between congruent melting compounds, such as GdA12-NdA12.[19] In the Mg-Al-Zn system any composition section will cut at least one tie line or tie triangle, thus, no pseudobinary section exists.
For the isothermal or vertical 2D sections, such as in Fig. 8 and 9, the simple rule outlined above is again helpful: If we cross a phase boundary we either gain a phase or loose a phase. Start by reading the phase regions at 400 °C and Al80Zn20 in the single-phase FCC region in Fig. 9. With decreasing Al-content, at constant 20 wt.% Zn, we cross the phase boundary at 79.5 wt.% Al and must enter a two-phase region. From Fig. 8 it is obvious that this is the FCC + MgZn2 region, so we have gained the phase MgZn2, as correctly labeled in Fig. 9. The next boundary is at 75.9 wt.% Al and, according to the rule, it might be single- or three-phase. From Fig. 8 we see that this is the narrow three-phase region FCC + MgZn2 + τ, so we have gained the phase τ. At 75.3 wt.% Al we cross the boundary to the wide region labeled as FCC + τ in Fig. 9, so we have lost the phase MgZn2, in consistency with Fig. 8. Now it becomes obvious that the next phase boundary at 53.7 wt.% Al in Fig. 9, where we gain the phase β, reflects just the cut through the FCC + τ edge of the tie triangle FCC + τ + β in Fig. 8. All phase compositions of FCC, τ, and β, are way off the vertical section. For the example alloy Mg30Al50Zn20 compositions can only be obtained from the isothermal section, as detailed above. One may continue reading the 400 °C line in Fig. 9 and add labels to all phase regions in consistency with Fig. 8 and the “gain/loose-a-phase-rule”.
Invariant Equilibria
Invariant equilibria in the Mg-Al-Zn system generally comprise four phases and occur at a fixed temperature. Five phases may only occur if we include the gas phase at a distinct pressure, but that is not discussed here. In the 3D prism diagram the four-phase region forms a 2D area, spanned by the fixed composition points of the four phases. Precisely four different three-phase triangles merge at this temperature because each of the four phases, at unique composition, is in equilibrium with the three others. This four-phase plane may appear as a tetragon or as a triangle. The latter case is seen if one composition point is inside the largest three-phase triangle. One may see a glimpse of this four-phase plane in the vertical phase diagram section as a line, where the vertical section cuts through this tetragon or triangle.
In Fig. 9 this part of the four-phase region L + FCC + τ + β is seen as the horizontal line at 447.07 °C from 47.3 to 53.4 wt.% Al. That means that any alloy in that composition range will, on cooling from higher temperature, experience this invariant equilibrium. It is associated with a unique invariant reaction, in this case
which is a ternary eutectic reaction. It is emphasized that none of the phase compositions is located on that horizontal line in Fig. 9. The small part of the graph around that line appears misleadingly like a “binary eutectic”. The appearance may differ if the vertical section is selected in a different direction in the 3D prism. In fact, the composition of L is inside the largest three-phase triangle FCC + τ + β, forming the boundary of the four-phase plane. In any ternary eutectic the liquid completely decomposes into three phases. Here the reaction products are FCC + τ + β at 447.07 °C, so there is only one possible exit from this reaction, the FCC + τ + β region in Fig. 9.
The second possible reaction type occurs in the four-phase region L + γ + HCP + φ, seen as the horizontal line at 365.34 °C from 9.2 to 29.5 wt.% Al in Fig. 9. All alloys in that composition range will go through the invariant reaction
which is a ternary transition-type reaction. The liquid reacts with γ to form HCP + φ and, depending on the initial phase fractions of L and γ, there are two possible exits from this reaction, either HCP + φ + L or HCP + φ + γ, because some unreacted excess of an initial phase may remain together with the newly formed phases HCP + φ. If the initial fractions of L + γ are exactly balanced a special exit into the two-phase region HCP + φ is possible, as seen in Fig. 9. It is obvious that the general “gain/loose-a-phase-rule” cannot hold at such special points, here the transition from the phase region L + γ + HCP + φ occurs to HCP + φ. The rule only holds for extended boundaries, not for special points. More examples of special points are presented in the next paragraph. In a transition-type reaction the composition of L must be outside the three-phase triangle of the solid phases, here γ + HCP + φ, and the boundary of the four-phase plane is a tetragon.
The last possible reaction type occurs in the four-phase region L + τ + γ + φ, seen as the horizontal line at 387.37 °C from 30.2 to 31.7 wt.% Al in Fig. 9. Any alloy in that composition range will go through the invariant reaction
which is a ternary peritectic reaction. The three phases L + τ + γ react to form φ. Depending on the initial phase fractions there are three possible three-phase exits from this reaction, either φ + L + τ, or φ + L + γ, or φ + τ + γ. In the peritectic reaction type the composition of the formed phase φ must be inside the three-phase triangle of the reactant phases, here L + τ + γ, and the boundary of the four-phase plane is this triangle.
In Fig. 9, because of the selected composition cut through this four-phase plane, one sees only two of the possible three-phase exits to lower temperature, φ + L + γ, and φ + τ + γ. In between there is the special case that reaction (11) ends with the two-phase equilibrium φ + γ because the initial phase fractions of L and τ are balanced, so they react completely. A very special case, not seen in Fig. 9, occurs if all initial phase fractions are balanced and the reaction ends with complete formation of single-phase φ only. That requires the alloy composition to be exactly identical to the unique composition point of φ at 387.37 °C; this temperature is also the thermal stability limit of φ. Upon heating such an (equilibrated) single-phase alloy it will decompose at 387.37 °C into the three phases given by Eq 11, a process that can be viewed as a reverse eutectic type reaction. A note of warning regarding kinetics should be considered. Similar to the binary peritectic/peritectoid reaction the ternary one in Eq 11, and to some extent also the transition-type reaction, Eq 10, slows itself down because the solid product phase forms a growing diffusion barrier between the reactant phases. As opposed to that, the ternary eutectic reaction is more likely to occur completely even at faster cooling rates due to its decomposition type.
It is emphasized that only three types of invariant reactions may occur in ternary systems: eutectic type (decomposition), transition-type, and peritectic type (formation). Depending on the kind of phases involved one may find special names, such as eutectoid if a solid phase decomposes into three others. The important point is to realize which type of invariant reaction (not which name) occurs because it provides an indication if this reaction is likely to occur under real world cooling conditions.
If all phases involved in a ternary invariant reaction were exactly stoichiometric phases the above discussion reduces to the simple classical chemical reaction equation, such as A2B + B2C = B3C + A2. That highlights the power of the phase diagram approach. Even if only one of these phases, e.g. A2B, is a phase with distinct solution range the classical chemical reaction equation becomes very cumbersome or inapplicable. Moreover, the information about neighboring three- and two-phase relations cannot be given that way. The phase diagram, however, provides the comprehensive information on all equilibrium phase relations and reactions/transformations in a clear, concise and precise manner.
Liquidus Projection
For melting and solidification processes the equilibria of the liquid with solid phases are especially important. The extensions of the liquidus lines from the binary edges form the liquidus surface in the 3D prism and its projection to the composition triangle forms the liquidus projection, shown in Fig. 10. It immediately answers the question which phase crystallizes primary. For any alloy composition in the region marked “HCP” this is the primary phase that may grow freely in the melt, thus forming a typical dendritic or globulitic microstructure. In the adjacent primary γ region this intermetallic will form first from the melt. At the intersection line the liquid phase compositions are in equilibrium with both HCP and γ; the liquid is double saturated. This intersection line displays the projection of the monovariant three-phase equilibrium L + HCP + γ. It emerges from the Mg-Al edge were it starts as the binary invariant eutectic reaction L = HCP + γ at 436.3 °C, proceeding to lower temperature into the ternary. At 400 °C it is seen as the tie triangle L + HCP + γ in Fig. 8. The triangular shape tells that it is monovariant, at a given temperature all three phase compositions are fixed. Only the trace of the apex at phase L is plotted in the projection in Fig. 10, the solid compositions would make that graph too busy. Each primary phase region is confined by such monovariant lines of double saturated liquid, or by the binary edges.
At an intersection point of different monovariant lines we have a contact point of three primary phase regions, such as FCC, τ, and β. That unique liquid composition is (triple) saturated with all three phases, thus forming the four-phase equilibrium L + FCC + τ+β. That is exactly the invariant reaction of Eq 9, associated with the unique temperature of 447.07 °C in the projection. Therefore, Fig. 10 reveals all the liquid compositions involved in invariant equilibria. One simply reads the types of the three adjoining primary regions, e.g. τ, γ, and φ to see the composition of L in the invariant L + τ + γ = φ at (34.7 wt.% Zn, 14.7 wt.% Al) and 387.37 °C, discussed in Eq 11.
In total there are 12 different invariant four-phase reactions in the Mg-Al-Zn system corresponding to the intersection points in Fig. 10. The closing of the tiny primary field of Mg5Zn2, at 52 wt.% Zn, 0.1 wt.% Al and 338.9 °C, produces the 12th point, which cannot be discerned on the graph. These invariant reactions are connected by the network of monovariant three-phase equilibria, some of them ending in the binary edges, some just occur in the ternary, such as L + τ + MgZn2. This line offers a special case, the maximum at 530.1 °C with liquid composition (13.4 wt.% Al, 64.4 wt.% Zn). The maximum occurs because the tie triangle L + τ + MgZn2 degenerates to a line and at exactly this point the three-phase equilibrium becomes a unique and invariant three-phase reaction,
This reaction is of the eutectic type because the liquid composition is located exactly in between the τ + MgZn2 tie line. Therefore, the liquid may decompose into these two solid phases without any composition shift. That explains why this reaction is invariant, similar to the binary eutectic. Other double saturated lines show a monotonous temperature variation only, such as L + MgZn2 + FCC from 475.9 °C down to 355.4 °C at the Zn-rich end. One should be careful in assigning a reaction type because it may change within the monovariant range and the transition from eutectic to peritectic type may be hard to detect especially if significant solid solubilities are involved.[2] The safest way, also for multicomponent alloys, is to calculate the phase fractions with a small decreasing temperature step for a given alloy composition and temperature. The shrinking phases go to the left hand side and the growing phases to the right hand side of the reaction equation, valid only at that state point. It can be shown that even within a given tie triangle the transition from eutectic (α = β + γ) to peritectic (α + β = γ) type may occur by just changing the alloy composition at fixed temperature. Therefore, one should generally denote just the three-phase equilibrium (α + β + γ) unless it degenerates to an invariant reaction at a minimum or maximum temperature, such as in Eq 12.
A 2D graphical display of the network of monovariant three-phase equilibria, connecting the invariant reactions of the binary edge system with those in the ternary system, can be given by the “Scheil Reaction Scheme”.[20] It may be used to prove the consistency of the phase diagram; for example the number of three-phase equilibria meeting at a four-phase reaction must be four, and so on. An established notation for invariant equilibria and liquidus projections is developed[21] that covers also more complex cases, such as liquid miscibility gaps intersecting primary crystallization fields in a liquidus surface.
A particularity of the primary regions of φ and τ in Fig. 10 is that they do not touch the binary edges. That may be seen as another indication that φ and τ are true ternary solid phases, however, the decisive distinction is that their solid solution ranges do not touch the binary edges at any temperature. As additional information the projections of selected isothermal liquidus lines are plotted in Fig. 10. These contour lines give a better impression on the shape of the liquidus surface in the 3D prism phase diagram. Moreover they are used to read, or interpolate, the liquidus temperature of a given alloy in addition to the type of primary phase that starts crystallizing at that temperature.
Phase Diagram Applications Exemplified with Mg-Al-Zn
For melting processes the completely molten (single-phase liquid) region needs to be identified and that is obviously done from Fig. 7 to 10. For solution heat treatment the single-phase solid regions must be known, given in Fig. 7 to 9. Similarly the constitution of a ternary multiphase material is read from these diagrams to answer the question if the observed phase assembly is a stable one, or which assembly may be expected after equilibration. For solidification applications the important information on liquidus temperatures and primary crystallizing phase has been discussed above. The equilibrium melting/freezing range may be read from vertical sections, such as in Fig. 9.
A very powerful tool is the calculation of phase fractions (and compositions) of a fixed alloy composition of interest, such as shown in Fig. 5 and 6 for the binary example. That will be demonstrated in detail in the section on Scheil and equilibrium solidification simulation. In principle the equilibrium phase fractions could be read from a series of isothermal sections using the lever rule. That is only simple if the solid phases are all stoichiometric, in that special case even the liquidus projection and knowledge of the stoichiometries is sufficient. In a real world alloy system, with significant solid solubilities, the tie lines and their directions change with temperature, making this a very tedious manual task even if many isothermal sections in small temperature steps are available. The thermodynamic calculation using a software package and a reliable database is highly recommended for that application.
Another very important application is materials compatibility, applied in interface reactions, joining, durability of refractory crucibles for alloy melting, attack of slag, and so on. Initially two materials A and B are brought in contact and heated. For example, if the alloy plate composed of Mg80Zn20 is clamped to another one, Al80Zn20 (wt.%), the phase diagram in Fig. 9 reveals that in the temperature range 300-400 °C various product phases may form between the materials, and also partial melting may occur. At 400 °C more details are seen from Fig. 8, the dotted line at 20 wt.% Zn indicates all possible overall compositions of the clamped material system. All the phase regions crossed by that line indicate potential temporary product phases and the state point, calculated from the overall composition of the two plates, gives the final equilibrium state.
As another example, consider a thin film layer of an alloy Mg60Zn40 (wt.%) deposited on a disk of pure Al and then heating the coated disk at 400 °C. We apply the same technique as in section 3.2, the Cu-Ni example. In a first step we plot the initial composition of materials into Fig. 8, one point at pure Al the other at alloy Mg60Zn40. The phase diagram tells us that there is no tie line between these points, thus, there is no equilibrium and therefore a reaction is expected. In a second step we calculate or estimate the overall composition of this (closed) system, which must be on the straight line between the starting points. For a very thin film our state point will be in the single-phase FCC region, thus, after equilibration all the Mg and Zn atoms from the film will be dissolved in the (Al) disk. The disk converts to a solid solution that is eventually homogenized by solid state diffusion. Temporarily a partial melting of the film may occur, because that point is in the L + HCP region. After some Al from the disk went into the layer even a temporary complete liquid layer might form on the disk. Subsequently a number of reactions may occur, involving the phases τ, γ, and β, until the equilibrium state, dictated by the state point, is reached. With growing film thickness the state point may be located beyond the (Al) solvus in the adjacent two-phase region FCC + τ, and the τ phase is expected as final secondary phase on the saturated (Al) solution phase. With even larger film thickness, say total mass 5 g film on a thin Al disk of 5 g, the state point is located at Mg30Al50Zn20 (wt.%) and the three-phase equilibrium phase assembly FCC + τ + β, well discussed above, constitutes the final state of the reaction.
Stable and Metastable Phase Diagrams
The most important example of stable and metastable phase diagrams is found in the iron-carbon system, which is also of highest technological relevance for both steel and especially the two forms of cast iron, white iron and grey iron. The iron-carbon phase diagram in Fig. 11 is shown in many textbooks, but actually hard to read for two reasons: (i) it is the superposition of the stable and metastable phase diagram, and (ii) only the Fe-rich part is shown so it is not obvious which phases are connected by the tie lines. Let us resolve this by the following series of simpler phase diagrams.
Carbon atoms may be dissolved in the Fe-rich solution phases L, FCC (γ), and BCC (α or δ). Beyond the solubility limit carbon may precipitate either as graphite, Cgra, or as the stoichiometric compound cementite, Fe3C. The stable phase diagram in Fig. 12a reveals that graphite is the stable form at all temperatures, because Fe3C does not exist in equilibrium and is not seen. The gas phase is suppressed in Fig. 12(a) for simplification around the melting point of graphite at 4492 °C. From that point the liquidus line develops to lower temperature. The solidus line coincides with the temperature axis because the Fe solubility in graphite is negligible. The interesting part of this diagram is enlarged in Fig. 12(b), showing a simple phase diagram with three invariants:
In practical casting of Fe-C alloys, however, the nucleation kinetics of graphite is very slow. Even at the low cooling rates of sand casting the formation of Cgra is hindered and the next stable phase will precipitate from the supersaturated (and supercooled) liquid. This “next stable phase” is cementite, Fe3C. These conditions are simulated in the phase diagram calculation by suppressing (suspending, excluding) the formation of Cgra and the result is the metastable phase diagram shown in Fig. 13(a). Here cementite, Fe3C is the only C-rich solid phase. The C-rich part with pure liquid is hypothetical because at such high supersaturation the formation of graphite could not be prevented in the real world. The enlargement in Fig. 13(b), however, is real because at alloy compositions below 25 at.% C these phase relations are truly observed in solidification experiments because of the nucleation problems of graphite. We see three invariants in Fig. 13(b):
Note that the peritectic is identical in Eq 13 and 16 because carbon only occurs as dissolved atom in the Fe-rich phases. The eutectic L = γ + Fe3C forms a particular microstructure denoted as ledeburite and found in so called white iron. That name stems from the color shown by fracture. The eutectoid γ = α + Fe3C also forms a particular microstructure denoted as pearlite. Both microstructures are metastable because the phase Fe3C is metastable. By heating (tempering) such a Fe3C containing alloy at, say, 1000 °C the equilibrium phase graphite will form by decomposition of Fe3C.
That is seen by the superposition of the metastable and stable phase diagrams in Fig. 14 and its enlargement in the initial diagram, Fig. 11. The dashed lines denote the metastable and the solid lines the stable phase diagram. All equilibria among the phases L, δ, γ, and α are exactly identical in both diagrams, because the carbon atoms are dissolved with composition below the solubility limits with respect to Cgra or Fe3C. For a cast alloy with constitution γ + Fe3C tempered at 1000 °C it is seen that both phase compositions are located inside the heterogeneous two-phase region γ + Cgra. Therefore, the Fe3C will decompose forming graphite and some γ phase, and the initially supersaturated γ (6.76 at.% C) will also precipitate carbon as graphite to attain the lower equilibrium composition, 6.62 at.% C. The observed supersaturation is also consistent with the fact that the metastable eutectic and eutectoid, Eq 17 and 18, are at a lower, supercooled, temperature compared to the stable eutectic and eutectoid, Eq 14 and 15.
Both phase diagrams, Fig. 12(b) and 13(b), are correct and useful if chosen for the appropriate process. For melting iron in a graphite crucible or for heat treating Fe-C alloys one should consult the stable diagram, Fig. 12(b). For casting Fe-C alloys one should apply the metastable diagram, Fig. 13(b). Obtaining graphite in cast iron alloy is usually achieved by adding some silicon to the melt. In the Fe-C-Si ternary system the result of competition among the solidifying phases is different from the binary Fe-C system and formation of Cgra is promoted. That is clearly seen in Fig. 15, the Fe-C-Si isothermal phase diagram section at 1200 °C. It is in fact the extension of Fig. 11 into the ternary at 1200 °C. Below 20 at.% C only the stable phase diagram is indicated, at higher carbon content the superimposed dashed lines show the metastable Fe3C formation and the L + Fe3C phase region. The different slopes of the stable graphite liquidus line, L/L + Cgra, and the metastable cementite liquidus line, L/L + Fe3C, clearly show the increasing distance with Si-addition. Therefore, at 1 at.% Si more supersaturation is required to produce metastable Fe3C instead of stable Cgra, compared to the binary edge system with zero Si. As a result, graphite may precipitate easily during casting from Fe-C-Si ternary alloys and so-called gray iron is produced with different properties and color shown by fracture compared to white iron.
Other alloying elements may have an opposite effect, especially chromium. In the Fe-C-Cr system the slope of the stable graphite liquidus line, L/L + Cgra, is tilted to the C-rich side, thus cementite is stabilized and moreover the additional carbide M7C3. Such white cast iron alloys often show excellent wear resistance. The Fe-C-Cr phase diagram was extensively used in the successful development of such an alloy with low liquidus point and narrow freezing range.[22]
The consideration of stable and metastable phase diagrams is especially effective if supported by thermodynamic calculations. That enables quantitative calculation of supersaturation compositions, supercooling temperatures and, last not least, the thermodynamic driving forces. The results of such calculations can be clearly presented in the comparison of stable and metastable phase diagrams as done in this section. The point is that suppressing (or excluding) one or more specific phases, expected to be hindered by a higher nucleation/growth barrier, constrains the Gibbs energy minimum calculation to a smaller set of available phases. That calculation provides the quantitative distribution of all components on the remaining available phases at any state point. That has been successfully applied in many cases, for example to understand the different phase selection in as-cast and heat treated states of Mg-Ce and Mg-Nd alloys, in relation to the nucleation barriers of the second phase formation.[23] This approach is very powerful in multicomponent systems and was, for example, extended to understand as-cast and heat treated microstructures of ternary Mg-Ce-Nd alloys.[24]
Useful State Variables in Phase Diagrams
So far only the common state variables pressure, temperature and composition have been considered. Other state variables, such as activity or enthalpy may be even more useful depending on the actual materials process under consideration. That shall be briefly explained using the simple example of the binary Fe-C metastable phase diagram in Fig. 13b with graphite suspended. The metastability is not important in this section, this Fe-C system was simply chosen as a good example to demonstrate the general approach, valid for all systems. In the phase diagram shown in Fig. 16(a) with the state variables temperature and composition, here in wt.% C, the tie line L + γ at 1300 °C and the eutectic three-phase region L + γ + Fe3C are marked by lines, with dots indicating the phase compositions. This phase diagram is useful if the carbon content in the alloy is controlled by preparing a fixed alloy composition.
(a) Metastable Fe-C phase diagram in the temperature-composition plot. The tie line γ + L at 1300 °C is marked by the symbol  , and the three-phase equilibrium L + γ + Fe3C at 1148.4 °C is marked by the symbol
, and the three-phase equilibrium L + γ + Fe3C at 1148.4 °C is marked by the symbol  . (b) Metastable Fe-C phase diagram in the temperature-activity plot. The two-phase equilibrium γ + L at 1300 °C is marked by the symbol
. (b) Metastable Fe-C phase diagram in the temperature-activity plot. The two-phase equilibrium γ + L at 1300 °C is marked by the symbol  , and the three-phase equilibrium L + γ + Fe3C at 1148.4 °C is marked by the symbol
, and the three-phase equilibrium L + γ + Fe3C at 1148.4 °C is marked by the symbol  . (c) Metastable Fe-C phase diagram in the enthalpy-composition plot. The tie line γ + L at 1300 °C is marked by the symbol
. (c) Metastable Fe-C phase diagram in the enthalpy-composition plot. The tie line γ + L at 1300 °C is marked by the symbol  , and the three-phase equilibrium L + γ + Fe3C at 1148.4 °C is marked by the large red triangle. The application to the cooling path of an alloy with constant 3 wt.% C, marked by the dashed line 0-1-2-3-4, is discussed in the text. (d) Enthalpy-activity plot along the phase boundaries of the metastable Fe-C system. This is not a true phase diagram
, and the three-phase equilibrium L + γ + Fe3C at 1148.4 °C is marked by the large red triangle. The application to the cooling path of an alloy with constant 3 wt.% C, marked by the dashed line 0-1-2-3-4, is discussed in the text. (d) Enthalpy-activity plot along the phase boundaries of the metastable Fe-C system. This is not a true phase diagram
In other metallurgical processes, such as carburization of an iron alloy through the gas phase, the carbon content is not fixed because the system is open. The state point can be controlled in that process by the carbon activity in the gas phase, a C. Useful gas mixtures are CO + CO2, or CH4 + H2, and the carbon activity is fixed by the composition of the gas mixture that flows at given temperature over the Fe-alloy. The equilibrium phases in the alloy at any state point can be read from the phase diagram with T and a C plotted as state variables in Fig. 16(b). In this diagram any two-phase region collapses to a line because both T and a C must be identical if the two phases are in equilibrium. The tie line γ + L at 1300 °C connecting the phases γ (1.27 wt.% C) and L (2.94 wt.% C) in Fig. 16(a) collapses to a “tie point” at a C = 0.34 and 1300 °C in Fig. 16(b).
The single-phase regions remain as areas, however, significantly enlarged as seen especially for Fe3C. This phase is present for a large range of activity a C, but shows a negligible composition variation in Fig. 16(a). Because graphite has been chosen as the reference state for a C, the dotted vertical line at a C = 1 indicates saturation with graphite. The entire region with a C > 1 in Fig. 16(b) is, thus metastable with respect to graphite. The part of the vertical line at a C = 1 passing through the liquid region represents the stable two-phase equilibrium L + graphite, seen as the wide heterogeneous region in Fig. 12(a). For any constitution in the supersaturated region the distance to the vertical line, or (a C − 1), is a measure for the thermodynamic driving force for precipitation of graphite.
The topology of the phase diagram in Fig. 16(b) is the same as in the temperature-pressure diagram of a pure component in Fig. 2 because the state variables are potentials, which must have the same value in equilibrated phases. Therefore, in both diagrams, single-phase regions are areas, two-phase regions are lines and the invariant three-phase equilibrium is a point. The point a C = 1.036 and 1148.4 °C in Fig. 16(b) is the three-phase equilibrium L + γ + Fe3C, because the three single-phase regions meet at that point. The phase compositions and also the eutectic reaction type, Eq 17, cannot be obtained from Fig. 16(b) but only from Fig. 16(a). These two phase diagrams are complementary and just a different view on the same phase diagram. In fact, once Fig. 16(a) has been calculated no additional phase equilibrium calculation is required for Fig. 16(b) because the values of all relevant thermodynamic properties along the phase boundaries are already stored in the memory during this first phase diagram calculation. It is just a plot of different state variables of the same phase diagram, and that applies also to the following two diagrams.
The enthalpy, or heat content, of an alloy at given composition is important in many melting, solidification and heat treatment processes. Thus, the enthalpy-composition phase diagram in Fig. 16(c) is useful. The single-phase regions remain to be areas, as in the other two phase diagrams. The two-phase regions are heterogeneous areas, as in Fig. 16(a), however the tie lines are not horizontal. The tie line γ + L at 1300 °C is plotted with the coordinates γ (1.27 wt.% C, 49.6 kJ/mol) and L (2.94 wt.% C, 60.1 kJ/mol) because at the same temperature the liquid and solid phases exhibit different enthalpy. That is obvious at the melting “point” of pure iron at 1538 °C, showing the enthalpy-of-melting gap between 72.4 and 58.7 kJ/mol in Fig. 16(c). Most strikingly, the three-phase equilibrium regions also appear as areas, the true tie triangles, in Fig. 16(c). For example the region γ + L + Fe3C is spanned by the triangle with the coordinates γ (2.05 wt.% C, 45.0 kJ/mol), L (4.38 wt.% C, 54.0 kJ/mol), and Fe3C (6.69 wt.% C, 40.2 kJ/mol).
This clearly demonstrates that any “three-phase equilibrium region” could appear as a 0D point, Fig. 16(b), or as a 1D line, Fig. 16(a), or as a 2D triangle, Fig. 16(c). This different appearance is due to the fact that the selected state variables fall into two different groups: (i) potential variables, which have the same value in each equilibrated phase, such as T = 1148.4 °C and a C = 1.036 (or chemical potential of C) in the three-phase equilibrium L + γ + Fe3C; (ii) molar variables, they have different values in each equilibrated phase, such as the molar enthalpy or the composition in at.% or wt.%, resulting in a heterogeneous region. These distinctions are discussed in detail in the book by Hillert.[2]
The following example demonstrates the application of Fig. 16(c) (refer also to Fig. 16a) during cooling of an alloy with constant 3 wt.% C. Starting from 1600 °C and H m = 72.5 kJ/mol (point 0) one must first extract heat to reach the liquidus point at 1295 °C and H m = 59.9 kJ/mol (point 1). The primary solidification step, L → γ, requires further extraction of heat down to H m = 48.8 kJ/mol (point 2) to reach 1148.4 °C, so the heat of solidification in this primary step is ΔH primarym = 11.1 kJ/mol. The subsequent invariant eutectic reaction L → γ + Fe3C is completed at constant 1148.4 °C by further extraction of heat down to H m = 43.9 kJ/mol (point 3); the eutectic heat of solidification in this secondary step is, thus, ΔH eutecticm = 4.9 kJ/mol. The alloy is now completely solidified with a total heat of solidification ΔH totalm = 16.0 kJ/mol. Further heat extraction down to H m = 28.6 kJ/mol (point 4) reduces the temperature of the two phases γ + Fe3C down to 726.6 °C. The subsequent eutectoid may be read in the same manner.
There are many other state variables, the values of which are obtained during the calculation of the phase diagram in Fig. 16(a), that may be selected for plotting. Some combinations result in a true phase diagram some do not. Just sticking to the ones we have seen so far, one might select to plot the molar enthalpy, H m, versus temperature along the phase boundaries. That is obviously nonsense because these two variables cannot define a state point on the Fe-C system. A more realistic choice might be to plot the molar enthalpy, H m, versus the carbon activity, as shown in Fig. 16(d). However, in the phase regions marked as “FCC?” and “Fe3C?” some phase boundary lines overlap, so Fig. 16(d) is not a true phase diagram. The first reason is that this is not a permissible set of conjugate variables, as given in the rules by Hillert.[2] The problem is that the enthalpy should be normalized to the number of moles of Fe, H mFe, rather than to the number of moles of atoms (Fe and C) as in the normal molar enthalpy, H m. This can be understood more intuitively because it is evident that by controlling the carbon activity the system is now open to a reservoir with defined carbon activity and the carbon content in the system is not fixed. Only the amount of Fe in the system is fixed. However, even plotting H mFe versus carbon activity, referred to graphite, does not result in a true phase diagram, as detailed in a recent work.[25] The second problem is the different choice of reference states in H mFe and a C, the solution is given by Agren and Schmid-Fetzer.[25] Here it is sufficient to emphasize that different state variables may produce very useful phase diagrams but one must be careful in the selection of state variable combinations[2,25] to ensure that true phase diagrams are obtained.
Zero-Phase-Fraction (ZPF) Lines
A very effective approach to multicomponent phase diagrams, plotted as 2D sections with one or two molar axes, is given by the concept of Zero-Phase-Fraction (ZPF) lines introduced by Morral.[26,27] This concept is illustrated for the simplest system Cu-Ni in Fig. 17(a) and (b).
For each individual phase (φ) a separate ZPF-line exists, ZPF(φ). There are two conditions along ZPF(φ): (i) the phase fraction of φ is zero, f φ = 0, and (ii) saturation with φ exists. Therefore, ZPF(φ) is a line of state points where the phase φ is at the verge of just manifesting as stable phase. This creates a simple topological boundary, splitting the 2D phase diagram in two parts. On one side of the line ZPF(φ) the phase φ does not exist, whereas on the other side it exists, maybe together with other phases. The superposition of ZPF-lines for all individual phases creates the phase diagram in this 2D section.
That is demonstrated in Fig. 17(a), where below ZPF(Liquid) no liquid exists, only FCC. Above ZPF(Liquid) the liquid phase is stable with f Liquid > 0. Therefore ZPF(Liquid) is the solidus line in the phase diagram, Fig. 3, it is the FCC/L + FCC phase boundary. The ZPF(FCC) is shown in Fig. 17(b), it is the liquidus line in Fig. 3. Only these two individual phases exist in the Cu-Ni system, thus, the superposition of Fig. 17(a) and (b) creates the phase diagram in Fig. 3. Within the two-phase region L + FCC one may plot a series of lines with constant liquid fractions, f Liquid from 0 to 1, which ends with f Liquid = 1 at the liquidus line; that construct is a phase fraction chart.[26] The usefulness of this ZPF approach is not evident in the simple binary Cu-Ni system because the phase diagram can be well understood without ZPF lines. However, the usefulness becomes evident in multicomponent systems, as will be shown in our now well-known Mg-Al-Zn example.
Figure 18(a) shows the vertical section of the Mg-Al-Zn phase diagram from alloy A (Mg80Zn20) to alloy B (Mg50Al50), wt.%. The Zn-content varies in linear relation with the Al-content on the abscissa, as seen by plotting that composition section into the isothermal section in Fig. 8, or 7. In the liquidus projection, Fig. 10, this section cuts the liquidus surface along the liquidus lines of the HCP and γ phases, and that is reflected in Fig. 18(a) as the phase boundary of the single-phase liquid region. Only four ZPF lines are highlighted here, ZPF(L), ZPF(HCP), ZPF(γ), and ZPF(φ). The labels are given on the “outside” of the ZPF lines where the phase does not exist. It becomes evident that ZPF(L) gives a very simple presentation of the solidus line for the series of alloys along this section. That is important in applications as a limit to avoid partial melting of an alloy during heat treatment.
(a) Vertical section of the Mg-Al-Zn phase diagram from alloy A (Mg80Zn20) to alloy B (Mg50Al50), wt.%. Four ZPF lines are highlighted, ZPF(L) (red), ZPF(HCP) (blue), ZPF(γ) (pink), and ZPF(φ) (green). See detail in b. (b) Magnified part of a. That section is from alloy A (Mg80Zn20) to alloy ab (Mg76.4Al6Zn17.6), wt.%. Alloy ab is also on the section in a at 6 wt.% Al
To identify the ZPF course for a specific phase, such as ZPF(HCP), the following rule is helpful. Generally, at an intersection of two different ZPF lines, the incoming line will continue by choosing the “middle course” of the three lines emerging from that point. That is seen clearly by following ZPF(HCP) in Fig. 18(a). Coming from higher temperature, the first intersection is with ZPF(γ) and ZPF(HCP) continues along the middle one of the three emerging lines, the paths to the right and left hand sides belong to ZPF(γ). The second intersection along the course of ZPF(HCP) is the one with ZPF(L), and ZPF(HCP) does not sway to the right or left but goes down to the edge at 300 °C and 41.4 wt.% Al. At special points, e.g. invariant reactions, this simple rule may not hold because parts of the ZPF lines may overlap.
The details in the Al-poor corner are shown in Fig. 18(b), the magnified part of Fig. 18(a). Here the ZPF(HCP) cannot be seen because the phase HCP is omnipresent in all phase regions of that vertical phase diagram section. Similarly, if a phase is absent in the entire section its ZPF line will also not be seen, and that is the case for ZPF(γ) in Fig. 18(b). Only ZPF(L) and ZPF(φ) are highlighted in Fig. 18(b) but not those for τ, Mg5Zn2, and MgZn.
In most cases any ZPF line would start and end at the edges of the 2D phase diagram section because it splits the diagram in two topologically different parts. That is also seen by following this example to envisage how the phase boundaries are composed of ZPF lines in another 2D section, for example ZPF(FCC) and ZPF(HCP) in the isothermal section in Fig. 7. This diagram also offers an example of a special case: ZPF(τ) in Fig. 7 cuts out an enclosed area, not touching any edge of the 2D section. The area is composed of the single-phase τ region and the adjoining two- and three-phase equilibrium regions involving τ. It is also possible that the 2D section is split in more than two parts by more than one ZPF line of the same phase. An example is given by the two lines ZPF(HCP) in Fig. 8. One takes course from the Mg-Zn to the Mg-Al edge, starting at the L/L + HCP line (at Mg53Zn47) and ending at the γ/γ + HCP line. The other, much shorter one, from the Mg-Zn to the Al-Zn edge is simply the liquidus line of Zn-rich HCP.
Coming back to the 2D section in Fig. 18(a) and counting all individual existing phases, they sum up to seven: L, HCP, γ, φ, τ, Mg5Zn2, and MgZn. However, 18 different phase regions (areas, single-, two- and three-phase) exist plus 6 invariant four-phase equilibrium regions (lines). That sums up to 24 different phase equilibria, actually seen in this section, compared to only 7 individual phases. Theoretically, in a ternary system with seven phases, even a much large number of such phase equilibria is possible by different combinations, namely 91, even though not all of them will become stable. In higher order systems this discrepancy between number of phases and number of possible phase equilibria dramatically increases. This highlights why modern software algorithms calculate 2D sections of phase diagrams by tracking just the individual ZPF lines, without worrying about two-, three-, four-, etc. phase equilibria. They result by superposition of the much smaller number of ZPF lines, because during the tracking the information about the saturated phases is also stored in the memory.
For reading and applying multicomponent phase diagrams the ZPF lines are most useful if the application aims at avoiding the occurrence of a specific phase. For example an intermetallic phase known to cause embrittlement after long time of service at elevated temperature, or heat treatment, may be avoided by selecting the alloy composition anywhere on the outside of its ZPF line.
Another application example is friction stir welding of different alloys. This process was applied to join an Al-alloy (AA5454) to a Mg-alloy (AZ91).[28] In order to understand the possible reactions and formation of phases by mixing these two materials the vertical phase diagram section in the relevant 5-component system Al-Mg-Mn-Fe-Zn was calculated. Minor amounts of Si, Cr, and Cu in these alloys were neglected for the calculation. Thus, the compositions of the alloys before welding were simplified to Al95.69Mg3Mn1Fe0.3Zn0.01 for AA5454 and Mg90.8Al8Zn1Mn0.2 for AZ91 (wt.%) in the 2D phase diagram section between these end members, as shown in Fig. 19.[28] In a closed system, given by this process, the overall composition of the system—or the state points—for any mixing ratio of these initial alloys can only vary along that composition axis. Only the variation of Mg (3-90.8 wt.%) is shown on the abscissa, however, the other compositions vary linearly coupled, Al (95.69-8 wt.%), Mn (1-0.2 wt.%), Fe (0.3-0 wt.%), and Zn (0.01-1 wt.%). The most important information obtained from that phase diagram section is highlighted by ZPF(Liquid) in Fig. 19. Below that red line any mixing ratio will remain solid, as intended because the friction stir welding process is envisaged as a solid-state process. Thus, the local temperatures in the welding zone during that process should be controlled to be lower than given by the red line to avoid partial melting. Moreover, the possible equilibrium product phases from that process in the solid state can also be read from the phase regions between the initial Al-alloy AA5454 and the Mg-alloy AZ91. With varying local overall composition within the welding zone the local state point may be expected to vary along that line.
This phase diagram approach is applied successfully to a wealth of reactions between different materials, for example coating/substrate reactions, such as multicomponent oxide thermal barrier coatings on various substrates that are multicomponent alloys like Ni-superalloys. Using thermodynamic software and an appropriate database the impact of temperature variation and minor or major composition changes in coating and/or substrate may be simulated to understand the phase and microstructure formation in the bonding or reaction zone. That is the basis to guide the materials engineer in focused optimization of materials and process selection for such complex devices.
Scheil and Equilibrium Solidification Simulation
The Scheil Approximation in Context of Multicomponent Multiphase Solidification
Equilibrium solidification simulation, discussed above, often does not reflect the phases actually observed in the as-cast state of alloys. That discrepancy is most pronounced if the crystallizing phases exhibit wide ranges of solid solubility and if solid-state diffusion is relatively slow compared to the solidification rate. Under these conditions the so-called “Scheil approximation” is widely applied as a much better description.
The Scheil approximation, and the explicit equation for binary alloys, originated from the classic work of Scheil.[29] It is occasionally also called the Scheil-Gulliver approximation. The earlier contribution of Gulliver,[30] who did not give an explicit equation, was put into perspective by Glicksman.[31] The classic Scheil equation describes the solid concentration, c s, as function of solid fraction f s, for a binary alloy with overall concentration c 0. Actually mole fractions are used since density differences are neglected. The normal solidification process, unidirectional with planar interface, is thought to occur by precipitation of sequential (infinitesimal) layers of a single solid solution phase. Four key assumptions are made to arrive at that equation by application of a differential mass balance: (i) Local equilibrium at the liquid/solid interface prevails; (ii) The liquid phase is perfectly mixed; (iii) No solid-state diffusion occurs during and after solidification; (iv) The distribution coefficient, k 0, is assumed to be constant and relates the concentration ratios at the liquid/solid interface to a “linearized” binary phase diagram. This classic Scheil equation is found in many textbooks on solidification, e.g.:[31]
However, it cannot be applied to real-world scenarios of multicomponent alloys with different types of solid phases precipitating. A most significant progress has been made by combining Calphad-type generated thermodynamic databases with the basic Scheil approximation in assumptions (i)-(iii), but releasing assumption (iv). The precipitation of sequential (infinitesimal) layers of any assembly of solid phases is quantitatively calculated from the current local equilibrium at the liquid/solid(s) interface. That is solved for each “layer step” by numerical procedures which are available in software packages such as Pandat,[5] Thermocalc[6] or Factsage.[7] In this modern approach the concept of a “distribution coefficient k 0” is not used at all. Rather the calculation of the multicomponent equilibrium tie line (or tie triangle etc. for multiphase solidification) at each temperature at the liquid/solid(s) interface is embedded in the numerical procedure. That is the basis for the most successful application of the Scheil approximation to real-world multicomponent multiphase alloys. It allows to quantitatively calculate a limiting case for the various solid phase fractions and phase composition gradients (segregation) developing in the Scheil-freezing-range of the alloy by using thermodynamic data only without requiring any kinetic material parameter.
This Scheil approximation is often much more realistic compared to the other limiting case, the “equilibrium” or “lever rule” approximation, where assumption (iii) is replaced by assuming infinitely fast solid-state diffusion and, thus, complete equilibration also in all solid parts of the alloy at any temperature. This “equilibrium” condition requires complete diffusion back into the regions crystallized at an early stage, which may be far remote from the liquid/solid interface at a late stage of solidification. Results of such line calculations under equilibrium conditions, also done numerically, were shown in Fig. 5 and 6. Again, the concept of “k 0” is not used at all.
Therefore, the calculation of both the “Scheil approximation” and the “equilibrium approximation” often provides useful bounds to assess the solidification of a multicomponent alloy and to gain insight in heat treatment conditions. Another limitation in both approximations is that any nucleation or growth undercooling is assumed to be zero. The two main limitations in the Scheil approximation are: (i) The diffusion layer in the liquid in front of the moving interface is neglected; it will be build up by concentration accumulation if the solubility of the pertinent component is larger in the liquid compared to the solid (or depletion in the other case). (ii) Back diffusion is completely excluded, even if the concentration gradient in a solid phase may be very steep at the final stage of solidification or if the component is known as fast diffusing. However, to quantitatively address these two limitations kinetic data are required, such as diffusion coefficients in all phases, or better the mobilities because diffusion coefficients can then be calculated using the thermodynamic factors obtained from the already known thermodynamic description. That is done in advanced solidification models that may also take the convection in the liquid into account as another transport mechanism. However, kinetic data are often not known for real multicomponent systems, leaving the Scheil approximation as the best alternative.
For special cases, if one component is known to diffuse very fast in the solid phases it could be set as diffusing infinitely fast, while the diffusion of all other components is kept completely blocked. In that case partial back diffusion is simulated in a partial equilibrium of the homogeneous residual liquid with the solid(s).[32,33] This is related to the paraequilibrium conditions of ternary (or higher order) systems with two sluggishly diffusing components, such as substitutional Fe and Mn, and the fast diffusing interstitial C.[2] That approach is especially useful if the interstitial components occur in phases with wide solid solution range, such as carbon in the austenite (FCC) phase of steel.
If all solid phases exhibit negligible solid solution range and only eutectic (no peritectic or transition-type) reactions occur, the Scheil simulation will give exactly the same results as the equilibrium solidification simulation. The reason is simply that the condition to block the diffusion in the solid phases will not make a difference because it is impossible to build up a concentration gradient in a stoichiometric solid phase, requiring solid-state diffusion to be leveled out. That also explains why the equilibrium (or lever rule) solidification calculation works nicely in simple eutectic systems.
Solidification Simulation Exemplified with Mg-Al-Zn
The different features of these two limiting cases, the equilibrium and Scheil approximation, respectively, will be exemplified for the solidification simulation of a ternary Mg90Al9Zn1 (wt.%) alloy. That is the simplified nominal alloy composition of the important magnesium casting alloy AZ91. Its overall composition is plotted as the starting point in Fig. 20, the Mg-rich part of the Mg-Al-Zn liquidus projection.
Mg-rich part of the Mg-Al-Zn liquidus projection. The Mg-rich HCP phase is denoted as (Mg), compare with Fig. 10. The solidification paths of alloy Mg90Al9Zn1 are superimposed for equilibrium and Scheil simulation, respectively
The blue curve is the solidification path under equilibrium conditions, showing the composition variation of the residual liquid phase while its fraction shrinks from 1 to zero. The liquid composition moves from Mg-Al9Zn1 at the liquidus temperature of 600 °C to Mg-Al23.6Zn10.3 at the solidus temperature of 446 °C. Simultaneously, the liquid phase fraction moves from 1 to zero as shown in Fig. 21, where a logarithmic scale is used. Concurrently, the solid phase (Mg) crystallizes and its fraction grows from zero to 1. Thus, solidification terminates without precipitation of any secondary phase. The reason is simply that all the alloying components can be dissolved in the (Mg) solid solution, attaining exactly Mg-Al9Zn1 at the solidus point, where a tie line stretches out to the last droplet of liquid at Mg-Al23.6Zn10.3. That is also seen in Fig. 8 – the solid solution range of HCP, or (Mg), is wide enough to cover the alloy composition Mg90Al9Zn1 even at 400 °C. This single-phase (Mg) region exists from 446 to 381 °C for this alloy, as seen in Fig. 21. Below that (solvus) temperature the secondary phase γ precipitates in a solid-state reaction from the (Mg) matrix phase. The solidification path in Fig. 20 is strongly curved to the Zn-rich side in the final stage. That is because the L + (Mg) tie lines, passing through the fixed Mg90Al9Zn1 point, rotate significantly with decreasing temperature. For practical applications the solution heat treatment window for this alloy from 446 to 381 °C in the single-phase (Mg) region is important.
The red curve in Fig. 20 is the solidification path under Scheil conditions. It starts at the same liquidus point as in the equilibrium case but then differs significantly. While crystallizing primary (Mg) the liquid composition moves in an almost straight line from Mg-Al9Zn1 to Mg-Al29.7Zn5.0 where it hits the monovariant line of double saturation, L + (Mg) + γ at 429 °C. This significant distinction to the equilibrium solidification arises because much less of the alloying components can be dissolved in the (Mg) phase due to the blocked back diffusion. The core of the first crystal, formed at 600 °C from Mg-Al9Zn1, remains frozen at the low composition of Mg-Al2.6Zn0.06. A remarkable composition gradient is formed in the growing (Mg) phase from that core crystal to the last layer solidified with composition Mg-Al11.7Zn0.5 at 429° C. At that point f (Mg) = 0.834 and f Liquid = 0.166, seen at the bend in the liquid fraction curve in Fig. 22. The solidification path in Fig. 20 also shows a break at that point, after which it continues with decreasing Al-content. Subsequently, the secondary phase γ crystallizes jointly with (Mg) from the melt in the monovariant reaction L → (Mg) + γ from 429 to 365.34 °C.
The next break point occurs at 365.34 °C (liquid composition Mg-Al1.7Zn34.3) where only a small amount of residual liquid is left, f Liquid = 0.004, and the accumulated solid fractions are f (Mg) = 0.886, and f γ = 0.110. At that point the invariant reaction L + γ = (Mg) + φ is encountered at 365.34 °C. This is a ternary transition-type reaction, and, as explained in Eq 10, the formation of the product phases (Mg) + φ would form a solid-state diffusion barrier. Therefore, this type of reaction cannot proceed under Scheil conditions, it is overrun. Solidification simply proceeds with the residual liquid, now saturated with (Mg) + φ. The amount of γ remains constant, that phase is frozen-in with f γ = 0.110. It will be overgrown by the following crystallizing phases, thus, loosing contact to the moving liquid/solid phase boundary. That is typical for such unreacted remains, or peritectic phases, often producing a characteristic microstructure.
The subsequent solidification L → (Mg) + φ occurs from 365.34 to 337.67 °C, producing the small fraction of φ, f φ = 0.002. Now the solidification path in Fig. 20 hits the next invariant reaction, L + φ = (Mg) + τ, at 337.67 °C. This is again a transition-type reaction that will be overrun in the Scheil simulation, the phase fractions do not change at this invariant point. Solidification proceeds with the residual liquid, f Liquid = 8.7 × 10−4, along the short line of L → (Mg) + τ in Fig. 20. Finally, the ternary eutectic L = (Mg) + τ + MgZn is encountered at 336.77 °C. This decomposition-type reaction proceeds fully, thus terminating solidification. The residual ternary eutectic liquid, f Liquid = 7.9 × 10−4, decomposes completely to produce some more (Mg) and τ and the additional phase MgZn. At this point, and at T < 336.77 °C, the alloy Mg90Al9Zn1 is composed of f (Mg) = 0.887, f γ = 0.110, f φ = 0.002, f τ = 1.1 × 10−4, and f MgZn = 3.4 × 10−4. These values are shown in Fig. 22 at the end of the various phase fraction curves and the point for MgZn.
This Scheil simulation of the as-cast constitution is complemented by the information about the sequence of phase precipitation, providing important clues on the schematic alloy microstructure with primary, secondary etc. phase formation. Moreover, the compositions of all phases are also obtained and could be plotted together with the phase fractions as function of the local phase formation temperature, revealing the expected segregation within the solid solution phases. In addition, the “Scheil solidus” at 336.77 °C is a good approximation of the incipient melting temperature of the as-cast alloy. That is an important temperature limit during extrusion or other hot forming processes. The assembly of five solid phases is of course a non-equilibrium constitution. Heating at 336 °C will eventually produce the equilibrium constitution (Mg) + γ with f (Mg) = 0.95 and f γ = 0.05, see Fig. 21, by dissolution of the non-equilibrium phases φ, τ, MgZn and leveling out the segregation in the solution phases. This also suggests a safe two-step heat treatment process, a first step slightly below 336 °C to avoid incipient melting and removing the low melting ternary eutectic, and a second step inside the solution heat treatment window, shown in Fig. 21, to produce a fully single-phase (Mg) alloy.
This concept of the incipient melting was applied as reverse “Scheil melting” to the frozen-in microstructure from a Scheil simulation and used to model the partial re-melting of feedstock in Thixomolding.[34] Care should be taken if the residual liquid fraction becomes very small. The example in Fig. 22 has been discussed until the termination of solidification in the ternary eutectic with f Liquid = 0 to highlight all aspects of the different reaction types in relation to the solidification path. This sequence of transition-type and eutectic reaction is also seen in many other ternary or multicomponent alloys and may be considered a generic example.
For practical applications, however, the calculation may be cut off at an arbitrary limit of f Liquid = 0.01 to obtain a “realistic Scheil solidus at 1% liquid “, in our example at 399 °C in Fig. 22. That corresponds to a “last liquid” composition of Mg-Al18.8Zn21.9 in Fig. 20, in the middle of the L → (Mg) + γ path. The next phase, φ, would only appear if the arbitrary cut-off limit is lowered to f Liquid = 0.001 (at 341 °C). The small phase fractions are not observed experimentally as shown in Fig. 23; the solidified microstructure of Mg90Al9Zn1 alloy only shows the phases (Mg) and γ. More importantly, it demonstrates that the coarse secondary phase γ crystallized jointly with (Mg) from the melt, thus proving the reaction L → (Mg) + γ predicted by the Scheil simulation as opposed to the equilibrium solidification in Fig. 21, where γ is formed by solid-state precipitation only. It is emphasized that the as-cast microstructure in Fig. 23 is obtained by a cooling rate of only 1 K/min.[35] Even this slow rate is fast enough to enable a good description by the Scheil approximation in this alloy system.
In other material systems it is even more important to set a cut-off limit to the Scheil solidus. If the Scheil simulation is not stopped by a eutectic it may fade out down to unrealistically low temperature with f Liquid ≪ 10−4, suggesting a much too wide freezing range and a too low incipient melting temperature. After all, the Scheil simulation is based on the approximations detailed above and may be prone to some artifacts if the liquid fraction becomes very small in the final stage.
For the correlation with actual casting defects other useful data may be obtained from Scheil simulations and phase diagrams. Generally, a narrow freezing range is beneficial. More precisely, the temperature range at the final stage of solidification is relevant. Quantitatively, the partial freezing range near termination of solidification, the terminal freezing range (TFR)[36] may be obtained from Scheil simulation. For example, this value may be taken from 88 to 98% fraction solid, indicating the TFR of the “almost” last 10% of solidifying liquid. This value is more relevant than the one for the “last 10%” because of the limitations of the Scheil approximations in the last 1 or 2% of liquid fraction. Secondly, a small TFR should be beneficial in order to avoid hot tearing. It is less useful to account for a limit of 0% liquid in that application instead of a small but not harmful residual limit. The experimentally observed hot-tearing susceptibility (HTS) has been successfully correlated to the phase diagram features of Mg-Al-Ca alloy castings: wide freezing range and low eutectic content result in higher HTS.[37] Scheil simulations have been used to reveal that the HTS increases with increasing fraction solid at the end of primary solidification of Mg-Al-Sr alloys.[38] This powerful tool was also used to predict and reduce liquation-cracking susceptibility during welding of Al alloys with different filler alloys by Scheil simulation of the respective solidified fractions.[39]
The superposition of the solidification path on the liquidus projection in Fig. 21 is very instructive for ternary alloys but hard to read and not recommended for more than three components. For quaternary or even higher multicomponent alloys the diagram types shown in Fig. 21 and 22 are widely used and simple to read, they may just show more phases. In addition, the Scheil simulation provides the compositions of all phases. It is instructive to plot these together with the phase fractions as function of the local phase formation temperature, revealing the expected segregation within the solid solution phases. For the quaternary Mg-Al-Zn-Mn alloy system such Scheil simulations have also been used to obtain the isotherms for the non-equilibrium solidus temperature (NEST), defined at the cut-off limit at 98% fraction solid, or f Liquid = 0.02. These predicted NEST isotherms are well validated by experimental data on incipient melting for the group of alloys with high alloying contents.[40]
Conclusion
-
1.
Phase diagrams are a cornerstone of knowledge in materials science and engineering. They are the perfect road map and starting point for designing all sorts of materials, such as alloys, ceramics, semiconductors, cement, concrete, or any material where the concept of phase is viable. They are also useful for optimization of closely related materials processes, such as melting, casting, crystal growth, joining, solid-state reaction, heat treatment/phase transformation, oxidation, vapor deposition, and so on. Many of these applications are exemplified in this work using phase diagrams of simple systems.
-
2.
Phase diagrams are entirely different from regular property diagrams, in which the diagram areas have no meaning. Any point in a phase diagram reflects a state point with unique constitution, defining the type, composition and fraction of phases in equilibrium. For a particular state point (fixed T, P, composition) the equilibrium is given by the global minimum of the Gibbs energy of the system, which is attained by smart distribution of the components on available phases.
-
3.
Simple classical chemical reaction equations, such as A2B + B2C = B3C + A2 are a very special case of the invariant reactions occurring in phase diagrams. The chemical reaction equation becomes very cumbersome or inapplicable if non-stoichiometric phases with distinct solution range are involved, typical for most liquid and the wealth of solid solution phases in real materials. Only the phase diagram provides the comprehensive information on all these and the adjoining equilibrium phase relations in a clear, concise and precise manner.
-
4.
The path from initial off-equilibrium state towards equilibrium is emphasized in many examples of phase diagram applications and also detailed for stable and metastable phase diagrams.
-
5.
State variables different from T, P, and composition, are useful in phase diagrams to control different processing conditions. Care should be taken when selecting different variables.
-
6.
The concept of Zero-Phase-Fraction (ZPF) lines is outlined as an effective approach to read and apply multicomponent phase diagrams. This is most useful if the application aims at avoiding the occurrence of a specific phase, for example an intermetallic phase known to cause embrittlement after long time of service at elevated temperature, or during heat treatment.
-
7.
Solidification simulation using the “Scheil approximation” in context of multicomponent multiphase solidification is quite different from the classic Scheil equation. It often provides a good estimate on the as-cast constitution or microstructure if solid-state diffusion is negligible. The other limiting case, the “equilibrium approximation”, is often more useful to gain insight in the constitution after heat treatment.
References
F. Rhines, Phase Diagrams in Metallurgy, Their Development and Applications, McGraw-Hill, New York, 1956, p 1-340
M. Hillert, Phase Equilibria, Phase Diagrams and Phase Transformations—Their Thermodynamic Basis, Cambridge University Press, Cambridge, 1998, p 1-538
Y. Austin Chang, S. Chen, F. Zhang, X. Yan, F. Xie, R. Schmid-Fetzer, and W. Alan Oates, Phase Diagram Calculation: Past, Present and Future, Prog. Mater Sci., 2004, 49, p 313-345
G. Humpston and D.M. Jacobson, Principles of Soldering and Brazing, ASM International, Materials Park, OH, 1993, p 71-110
W. Cao, S. Chen, F. Zhang, K. Wu, Y. Yang, Y. Chang, R. Schmid-Fetzer, and W.A. Oates, PANDAT Software with PanEngine, PanOptimizer and PanPrecipitation for Materials Property Simulation of Multi-Component Systems, Calphad, 2009, 33, p 328-342
J.-O. Andersson, T. Helander, L. Höglund, P. Shi, and B. Sundman, Thermo-Calc and DICTRA, Computational Tools for Materials Science, Calphad, 2002, 26, p 273-312
C.W. Bale, E. Bélisle, P. Chartrand, S.A. Decterov, G. Eriksson, K. Hack, I.-H. Jung, Y.-B. Kang, J. Melançon, A.D. Pelton, C. Robelin, and S. Petersen, FactSage Thermochemical Software and Databases: Recent Developments, Calphad, 2009, 33, p 295-311
H.L. Lukas, S.G. Fries, and B. Sundman, Computational thermodynamics: The Calphad Method, Cambridge University Press, Cambridge, 2007, p 1-313
R. Schmid-Fetzer, J. Gröbner: Thermodynamic Database for Mg Alloys: Progress in Multicomponent Modeling. Metals, 2012, 2, p 377-398 (Special Issue “Magnesium Technology”), doi:10.3390/met2030377, www.mdpi.com/2075-4701/2/3/377
M. Dirand, Z. Achour, B. Jouti, A. Sabour, and J.-C. Gachon, Binary Mixtures of n-Alkanes. Phase Diagram Generalization: Intermediate Solid Solutions, Rotator Phases, Mol. Cryst. Liq. Cryst., 1996, 275, p 293-304
R.J. Roe and W.C. Zin, Phase Equilibria and Transition in Mixtures of a Homopolymer and a Block Copolymer. 2. Phase diagram, Macromolecules, 1984, 17(2), p 189-194
D. Alfè, M. Gillan, and G.D. Price, Composition and Temperature of the Earth’s core Constrained by Combining Ab Initio Calculations and Seismic Data, Earth. Planet. Sci. Lett., 2002, 195, p 91-98
J. Groebner, H.L. Lukas, and F. Aldinger, Thermodynamic Calculation of the Ternary System Al-Si-C, Calphad, 1996, 20, p 247-254
W.D. MacDonald and T.W. Eagar, Isothermal Solidification Kinetics of Diffusion Brazing, Metall. Mater. Trans. A, 1998, 29(1), p 315-325
T. Studnitzky and R. Schmid-Fetzer, Diffusion Soldering for High Temperature Stable Thin Film Bonds, JOM, 2002, 54(12), p 58-63
T. Studnitzky and R. Schmid-Fetzer, Phase Formation and Diffusion Soldering in Pt/In, Pd/In and Zr/Sn Thin Film Systems, J. Electron. Mater., 2003, 32(2), p 70-80
V. Grolier and R. Schmid-Fetzer, Diffusion-Reactions in the Au-Rich Ternary Au-Pt-Sn System as a Basis for Ternary Diffusion Soldering, J. Electron. Mater., 2008, 37, p 815-828
A. Maître, M. François, and J.C. Gachon, Experimental Study of the Bi2O3-Fe2O3 Pseudo-Binary System, J. Phase Equilib. Diff., 2004, 25, p 59-67
J.H. Wernick, S.E. Haszko, and D. Dorsi, Pseudo-Binary Systems Involving Rare Earth Laves Phases, J. Phys. Chem. Solids, 1962, 23, p 567-572
H.L. Lukas, E.T. Henig, and G. Petzow, 50 Years Reaction Scheme after Erich Scheil, Z. Metallkd., 1986, 77, p 360-367
G. Effenberg and R. Schmid-Fetzer (Eds.), Critical Evaluation of Ternary Phase Diagram Data. Best Practice Guidelines for Evaluation & Notes for Authors, 6th ed, MSI, Materials Science International Services GmbH, Stuttgart, ISBN 3-932120-49-3, 2012, p 1-111
P. Huggett and B. Ben-Nissan, Development of a Low Melting Point White Cast Iron for Use in Composite Alloy Manufacture, Mater. Forum, 2007, 30, p 23-29
M.A. Easton, M.A. Gibson, D. Qiu, S.M. Zhu, J. Gröbner, R. Schmid-Fetzer, J.F. Nie, and M. Zhang, The Role of Crystallography and Thermodynamics on Phase Selection in Binary Magnesium-Rare Earth (Ce or Nd) Alloys, Acta Mater., 2012, 60, p 4420-4430
J. Gröbner, A. Kozlov, R. Schmid-Fetzer, M.A. Easton, S. Zhu, M.A. Gibson, and J.-F. Nie, Thermodynamic Analysis of As-Cast and Heat Treated Microstructures of Mg-Ce-Nd Alloys, Acta Mater., 2011, 59, p 613-622
J. Ågren and R. Schmid-Fetzer, True Phase Diagrams, Metall. Mater. Trans. A, 2014, 45A, p 4766-4769
J.E. Morral, Two-Dimensional Phase Fraction Charts, Scripta Metall., 1984, 18(4), p 407-410
J.E. Morral and H. Gupta, Phase Boundary, ZPF, and Topological Lines in Phase Diagrams, Scripta Metall. Mater., 1991, 25(6), p 1393-1396
O. Klag, J. Gröbner, G. Wagner, R. Schmid-Fetzer, and D. Eifler, Microstructural and Thermodynamic Investigations on Friction Stir Welded Mg/Al-Joints, Int. J. Mater. Res., 2014, 105, p 145-155
E. Scheil, Bemerkungen zur Schichtkristallbildung, Z. Metallkd., 1942, 34, p 70-72
G.H. Gulliver, The Quantitative Effect of Rapid Cooling Upon the Constitution of Binary Alloys, J. Inst. Met., 1913, 9, p 120-157
M.E. Glicksman, Principles of Solidification: An Introduction to Modern Casting and Crystal Growth Concepts, Springer, New York, 2011, p 1-550
Q. Chen and B. Sundman, Computation of Partial Equilibrium Solidification With Complete Interstitial and Negligible Substitutional Solute Back Diffusion, J. Jpn. Inst. Met., 2002, 43, p 551-559
E. Kozeschnik, W. Rindler, and B. Buchmayr, Scheil-Gulliver Simulation with Partial Redistribution of Fast Diffusers and Simultaneous Solid-Solid Phase Transformations, Int. J. Mater. Res., 2007, 98, p 826-831
A. Kozlov, M. Djurdjevic, and R. Schmid-Fetzer, Thermodynamic Simulation of Phase Formation During Blending of Mg-Alloys by Thixomolding, Adv. Eng. Mater., 2007, 9, p 731-738
M. Ohno, D. Mirkovic, and R. Schmid-Fetzer, Phase Equilibria and Solidification of Mg-Rich Mg-Al-Zn Alloys, Mater. Sci. Eng. A, 2006, 421, p 328-337
M.B. Djurdjevic and R. Schmid-Fetzer, Thermodynamic Calculation as a Tool for Thixoforming Alloy and Process Development, Mater. Sci. Eng. A, 2006, 417, p 24-33
G. Cao and S. Kou, Hot Tearing of Ternary Mg-Al-Ca Alloy Castings, Metall. Mater. Trans. A, 2006, 37, p 3647-3663
G. Cao, C. Zhang, H.Y. Cao, and S. Kou, Hot-Tearing Susceptibility of Ternary Mg-Al-Sr Alloy Castings, Metall. Mater. Trans. A, 2010, 41, p 706-716
G. Cao and S. Kou, Predicting and Reducing Liquation-Cracking Susceptibility Based on Temperature vs. Fraction Solid, Weld. J., 2006, 85, p 9-18
M. Ohno, D. Mirkovic, and R. Schmid-Fetzer, Liquidus and Solidus Temperatures of Mg-Rich Mg-Al-Mn-Zn Alloys, Acta Mater., 2006, 54, p 3883-3891
Author information
Authors and Affiliations
Corresponding author
Additional information
This article is an invited paper selected from presentations at the Hume-Rothery Award Symposium on “Thermodynamics and Kinetics of Engineering Materials,” during TMS 2014, held February 16-20, 2014, in San Diego, Calif., and has been expanded from the original presentation. This symposium was held in honor of the 2014 Hume-Rothery award recipient, Rainer Schmid-Fetzer, for his seminal contributions to alloy thermodynamics and phase diagrams, both computationally and experimentally.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Schmid-Fetzer, R. Phase Diagrams: The Beginning of Wisdom. J. Phase Equilib. Diffus. 35, 735–760 (2014). https://doi.org/10.1007/s11669-014-0343-5
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11669-014-0343-5


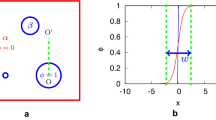





 , where dots indicate the phase compositions of the equilibrated phases at 12.7, 33.3, and 42.5 wt.% Al, respectively
, where dots indicate the phase compositions of the equilibrated phases at 12.7, 33.3, and 42.5 wt.% Al, respectively



 , is located in the three-phase region β + FCC + τ
, is located in the three-phase region β + FCC + τ













