Modeling and Simulation of Laser Processing of Particulate-Functionalized Materials

Abstract

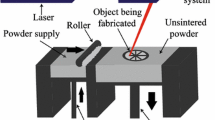
The objective of this paper is to focus on one of the “building blocks” of additive manufacturing technologies, namely selective laser-processing of particle-functionalized materials. Following a series of work in Zohdi (Int J Numer Methods Eng 53:1511–1532, 2002; Philos Trans R Soc Math Phys Eng Sci 361(1806):1021–1043, 2003; Comput Methods Appl Mech Eng 193(6–8):679–699, 2004; Comput Methods Appl Mech Eng 196:3927–3950, 2007; Int J Numer Methods Eng 76:1250–1279, 2008; Comput Methods Appl Mech Eng 199:79–101, 2010; Arch Comput Methods Eng 1–17. doi:10.1007/s11831-013-9092-6, 2013; Comput Mech Eng Sci 98(3):261–277, 2014; Comput Mech 54:171–191, 2014; J Manuf Sci Eng ASME doi:10.1115/1.4029327, 2015; CIRP J Manuf Sci Technol 10:77–83, 2015; Comput Mech 56:613–630, 2015; Introduction to computational micromechanics. Springer, Berlin, 2008; Introduction to the modeling and simulation of particulate flows. SIAM (Society for Industrial and Applied Mathematics), Philadelphia, 2007; Electromagnetic properties of multiphase dielectrics: a primer on modeling, theory and computation. Springer, Berlin, 2012), a laser-penetration model, in conjunction with a Finite Difference Time Domain Method using an immersed microstructure method, is developed. Because optical, thermal and mechanical multifield coupling is present, a recursive, staggered, temporally-adaptive scheme is developed to resolve the internal microstructural fields. The time step adaptation allows the numerical scheme to iteratively resolve the changing physical fields by refining the time-steps during phases of the process when the system is undergoing large changes on a relatively small time-scale and can also enlarge the time-steps when the processes are relatively slow. The spatial discretization grids are uniform and dense enough to capture fine-scale changes in the fields. The microstructure is embedded into the spatial discretization and the regular grid allows one to generate a matrix-free iterative formulation which is amenable to rapid computation, with minimal memory requirements, making it ideal for laptop computation. Numerical examples are provided to illustrate the modeling and simulation approach, which by design, is straightforward to computationally implement, in order to be easily utilized by researchers in the field. More advanced conduction models, based on thermal-relaxation, which are a key feature of fast-pulsing laser technologies, are also discussed.

Appendices

Appendix 1: Spatial Finite Difference Stencils

Following Zohdi [89–103], standard approximations are used:

• 1. For the first derivative of a primal variable u at $(x_1,x_2,x_3)$:

  $$\begin{aligned} \frac{\partial u}{\partial x_1}\approx \frac{u(x_1+\Delta x_1,x_2,x_3)-u(x_1-\Delta x_1,x_2,x_3)}{2\Delta x_1} \end{aligned}$$

  (6.1)

• 2. For the derivative of a flux at $(x_1,x_2,x_3)$, with an arbitrary material coefficient a:

  $$\begin{aligned} \frac{\partial }{\partial x_1} \left( a\frac{\partial u}{\partial x_1}\right)\approx &{} \frac{\left( a\frac{\partial u}{\partial x_1}\right) |_{x_1+\frac{\Delta x_1}{2},x_2,x_3} -\left( a\frac{\partial u}{\partial x_1}\right) |_{x_1-\frac{\Delta x_1}{2},x_2,x_3}}{\Delta x_1}\nonumber \\= &{} \frac{1}{\Delta x_1}\left[ a(x_1+\frac{\Delta x_1}{2},x_2,x_3)\left( \frac{u(x_1+\Delta x_1,x_2,x_3)-u(x_1,x_2,x_3)}{\Delta x_1}\right) \right] \nonumber \\&-\frac{1}{\Delta x_1}\left[ a(x_1-\frac{\Delta x_1}{2},x_2,x_3)\left( \frac{u(x_1,x_2,x_3)-u(x_1-\Delta x_1,x_2,x_3)}{\Delta x_1}\right) \right] , \end{aligned}$$

  (6.2)

  where we have used

  $$\begin{aligned} a(x_1+\frac{\Delta x_1}{2},x_2,x_3)\approx \frac{1}{2}\left( a(x_1+\Delta x_1,x_2,x_3)+a(x_1,x_2,x_3)\right) \end{aligned}$$

  (6.3)

  and

  $$\begin{aligned} a(x_1-\frac{\Delta x_1}{2},x_2,x_3)\approx \frac{1}{2}\left( a(x_1,x_2,x_3)+a(x_1-\Delta x_1,x_2,x_3)\right) \end{aligned}$$

  (6.4)

• 3. For the cross-derivative of a flux at $(x_1,x_2)$:

  $$\begin{aligned} \frac{\partial }{\partial x_2} \left( a\frac{\partial u}{\partial x_1}\right)\approx &{} \frac{\partial }{\partial x_2} \left( a(x_1,x_2,x_3)\left( \frac{u(x_1+\Delta x_1,x_2,x_3)-u(x_1-\Delta x_1,x_2,x_3)}{2\Delta x_1}\right) \right) \nonumber \\\approx &{} \frac{1}{4\Delta x_1\Delta x_2}( a(x_1,x_2+\Delta x_2,x_3)\left[ u(x_1+\Delta x_1,x_2+\Delta x_2,x_3)-u(x_1-\Delta x_1,x_2+\Delta x_2,x_3)\right] \nonumber \\&- a(x_1,x_2-\Delta x_2,x_3)\left[ u(x_1+\Delta x_1,x_2-\Delta x_2,x_3)-u(x_1-\Delta x_1,x_2-\Delta x_2,x_3)\right] ), \end{aligned}$$

  (6.5)

Fig. 11

Various Finite-difference stencils in “computational molecule” form (centered at $(x_i,x_j,x_k)$), where: (1) TERM-I: $a\frac{\partial u}{\partial x_i}$, (2) TERM-II:$\frac{\partial }{\partial x_i} \left( a\frac{\partial u}{\partial x_i}\right)$ and (3) TERM-III:$\frac{\partial }{\partial x_j} \left( a\frac{\partial u}{\partial x_i}\right)$, following Zohdi [89–103]

Remark

To illustrate second-order accuracy, consider a Taylor series expansion for an arbitrary function u

$$\begin{aligned} u(x+\Delta x)=u(x)+ \frac{\partial u}{\partial x}|_{x}\Delta x+ \frac{1}{2}\frac{\partial ^2u}{\partial x^2}|_{x}(\Delta x)^2 +\frac{1}{6}\frac{\partial ^3u}{\partial x^3}|_{x}(\Delta x)^3+{\mathcal{O}}((\Delta x)^4) \end{aligned}$$

(6.6)

and

$$\begin{aligned} u(x-\Delta x)=u(x)- \frac{\partial u}{\partial x}|_{x}\Delta x+ \frac{1}{2}\frac{\partial ^2u}{\partial x^2}|_{x}(\Delta x)^2 -\frac{1}{6}\frac{\partial ^3u}{\partial x^3}|_{x}(\Delta x)^3+{\mathcal{O}}((\Delta x)^4) \end{aligned}$$

(6.7)

Subtracting the two expressions yields

$$\begin{aligned} \frac{\partial u}{\partial x}|_{x} =\frac{u(x+\Delta x)-u(x-\Delta x)}{2\Delta x} +{\mathcal{O}}((\Delta x)^2). \end{aligned}$$

(6.8)

Appendix 2: Temporally-Adaptive Iterative Methods

Implicit time-stepping methods, with time step size adaptivity, built on approaches found in Zohdi [89–103] were used throughout the analysis in the body of the work. In order to introduce basic concepts, we consider a first order differential equation for a field ${{\varvec{W}}}$:

$$\begin{aligned} \dot{{{\varvec{W}}}}=\varvec{\Lambda }({{\varvec{W}}}), \end{aligned}$$

(7.1)

which, after being discretized using a trapezoidal “$\phi$-method” ($0\le \phi \le 1$)

$$\begin{aligned}{{\varvec{W}}}^{L+1}={{\varvec{W}}}^L+\Delta t \left( \phi \varvec{\Lambda }({{\varvec{W}}}^{L+1})+(1-\phi )\varvec{\Lambda }({{\varvec{W}}}^L)\right) . \end{aligned}$$

(7.2)

Generally, for systems of equations of this form, a straightforward iterative scheme can be written as

$$\begin{aligned}{{\varvec{W}}}^{L+1,K}={\mathcal{G}}({{\varvec{W}}}^{L+1,K-1})+{\mathcal{R}}, \end{aligned}$$

(7.3)

where ${\mathcal{R}}$ is a remainder term that does not depend on the solution, i.e. ${\mathcal{R}} \ne{\mathcal{R}}({{\varvec{W}}}^{L+1})$, and $K=1, 2, 3, ...$ is the index of iteration within time step $L+1$. The convergence of such a scheme is dependent on the behavior of ${\mathcal{G}}$. Namely, a sufficient condition for convergence is that ${\mathcal{G}}$ is a contraction mapping for all ${{\varvec{W}}}^{L+1,K}$, $K=1, 2, 3...$ In order to investigate this further, we define the iteration error as

$$\begin{aligned} \varpi ^{L+1,K} \mathop{=}\limits ^{\mathrm{def}}||{{\varvec{W}}}^{L+1,K}-{{\varvec{W}}}^{L+1}||. \end{aligned}$$

(7.4)

A necessary restriction for convergence is iterative self consistency, i.e. the “exact” (discretized) solution must be represented by the scheme

$$\begin{aligned}{\mathcal{G}}({{\varvec{W}}}^{L+1})+{\mathcal{R}}={{\varvec{W}}}^{L+1}. \end{aligned}$$

(7.5)

Enforcing this restriction, a sufficient condition for convergence is the existence of a contraction mapping

$$\begin{aligned} \varpi ^{L+1,K}=||{{\varvec{W}}}^{L+1,K}-{{\varvec{W}}}^{L+1}||= &{} ||{\mathcal{G}} ({{\varvec{W}}}^{L+1,K-1})-{\mathcal{G}}({{\varvec{W}}}^{L+1})|| \end{aligned}$$

(7.6)

$$\begin{aligned}\le &{} \eta ^{L+1,K} ||{{\varvec{W}}}^{L+1,K-1}-{{\varvec{W}}}^{L+1}||, \end{aligned}$$

(7.7)

where, if $0\le \eta ^{L+1,K}<1$ for each iteration K, then $\varpi ^{L+1,K}\rightarrow 0$ for any arbitrary starting value ${{\varvec{W}}}^{L+1,K=0}$, as $K \rightarrow \infty$. This type of contraction condition is sufficient, but not necessary, for convergence. Inserting these approximations into $\dot{{{\varvec{W}}}}=\varvec{\Lambda }({{\varvec{W}}})$ leads to

$$\begin{aligned} \displaystyle{{{\varvec{W}}}^{L+1,K}\approx \underbrace{\Delta t\left( \phi \varvec{\Lambda }({{\varvec{W}}}^{L+1,K-1})\right) }_{{\mathcal{G}}({{\varvec{W}}}^{L+1,K-1})} +\underbrace{\Delta t(1-\phi )\varvec{\Lambda }({{\varvec{W}}}^L)+{{\varvec{W}}}^L}_{{\mathcal{R}}}}, \end{aligned}$$

(7.8)

whose contraction constant is scaled by $\eta \propto \phi \Delta t$. Therefore, if convergence is slow within a time step, the time step size, which is adjustable, can be reduced by an appropriate amount to increase the rate of convergence. Decreasing the time step size improves the convergence, however, we want to simultaneously maximize the time-step sizes to decrease overall computing time, while still meeting an error tolerance on the numerical solution’s accuracy. In order to achieve this goal, we follow an approach found in Zohdi [89–103] originally developed for continuum thermo-chemical multifield problems in which one first approximates

$$\begin{aligned} \eta ^{L+1,K} \approx S(\Delta t)^p \end{aligned}$$

(7.9)

(S is a constant) and secondly one assumes the error within an iteration to behave according to

$$\begin{aligned} (S (\Delta t)^p)^K\varpi ^{L+1,0}=\varpi ^{L+1,K}, \end{aligned}$$

(7.10)

$K=1, 2,\ldots$, where $\varpi ^{L+1,0}$ is the initial norm of the iterative error and S is intrinsic to the system.⁷ Our goal is to meet an error tolerance in exactly a preset number of iterations. To this end, one writes

$$\begin{aligned} (S (\Delta t_{\mathrm{tol}})^p)^{K_{d}}\varpi ^{L+1,0}=C_{tol}, \end{aligned}$$

(7.11)

where $C_{tol}$ is a (coupling) tolerance and where $K_{d}$ is the number of desired iterations.⁸ If the error tolerance is not met in the desired number of iterations, the contraction constant $\eta ^{L+1,K}$ is too large. Accordingly, one can solve for a new smaller step size, under the assumption that S is constant,

$$\begin{aligned} \begin{array}{l} \displaystyle{\Delta t_{\mathrm{tol}} =\Delta t \left( \frac{(\frac{C_{tol}}{\varpi ^{L+1,0}})^{\frac{1}{pK_{d}}}}{(\frac{\varpi ^{L+1,K}}{\varpi ^{L+1,0}})^{\frac{1}{pK}}}\right) .} \end{array} \end{aligned}$$

(7.12)

The assumption that S is constant is not critical, since the time steps are to be recursively refined and unrefined throughout the simulation. Clearly, the expression in Eq. 7.12 can also be used for time step enlargement, if convergence is met in less than $K_d$ iterations.⁹

Appendix 3: Second-Order Temporal Discretization

Following Zohdi [89–103], discretization of temporally second-order equations can be illustrated by considering

$$\begin{aligned} \ddot{{{\varvec{U}}}}=\dot{{{\varvec{V}}}}=\varvec{\Psi }({{\varvec{U}}}). \end{aligned}$$

(8.1)

Expanding the field ${{\varvec{V}}}$ in a Taylor series about $t+\phi \Delta t$ we obtain

$$\begin{aligned}{{\varvec{V}}}(t+\Delta t)={{\varvec{V}}}(t+\phi \Delta t)+ \frac{d{{\varvec{V}}}}{d t}|_{t+\phi \Delta t}(1-\phi )\Delta t+ \frac{1}{2} \frac{d ^2{{\varvec{V}}}}{d t^2}|_{t+\phi \Delta t}(1-\phi )^2(\Delta t)^2+{\mathcal{O}}((\Delta t)^3) \end{aligned}$$

(8.2)

and

$$\begin{aligned}{{\varvec{V}}}(t)={{\varvec{V}}}(t+\phi \Delta t) -\frac{d{{\varvec{V}}}}{d t}|_{t+\phi \Delta t}\phi \Delta t+ \frac{1}{2} \frac{d ^2{{\varvec{V}}}}{d t^2}|_{t+\phi \Delta t}\phi ^2(\Delta t)^2+{\mathcal{O}}((\Delta t)^3) \end{aligned}$$

(8.3)

Subtracting the two expressions yields

$$\begin{aligned} \frac{d{{\varvec{V}}}}{d t}|_{t+\phi \Delta t} =\frac{{{\varvec{V}}}(t+\Delta t)-{{\varvec{V}}}(t)}{\Delta t}+\hat{{\mathcal{O}}}(\Delta t), \end{aligned}$$

(8.4)

where $\hat{{\mathcal{O}}}(\Delta t)={\mathcal{O}}((\Delta t)^2)$, when $\phi =\frac{1}{2}$. Thus, inserting this into the governing equation yields

$$\begin{aligned}{{\varvec{V}}}(t+\Delta t)={{\varvec{V}}}(t)+\Delta t\varvec{\Psi }(t+\phi \Delta t)+\hat{{\mathcal{O}}}((\Delta t)^2). \end{aligned}$$

(8.5)

Note that adding a weighted sum of Eqs. 8.2 and 8.3 yields

$$\begin{aligned}{{\varvec{V}}}(t+\phi \Delta t)=\phi{{\varvec{V}}}(t+\Delta t)+(1-\phi ){{\varvec{V}}}(t) +{\mathcal{O}}((\Delta t)^2), \end{aligned}$$

(8.6)

which will be useful shortly. Now expanding the field ${{\varvec{U}}}$ in a Taylor series about $t+\phi \Delta t$ we obtain

$$\begin{aligned}{{\varvec{U}}}(t+\Delta t)={{\varvec{U}}}(t+\phi \Delta t)+ \frac{d{{\varvec{U}}}}{d t}|_{t+\phi \Delta t}(1-\phi )\Delta t+ \frac{1}{2} \frac{d ^2{{\varvec{U}}}}{d t^2}|_{t+\phi \Delta t}(1-\phi )^2(\Delta t)^2+{\mathcal{O}}((\Delta t)^3) \end{aligned}$$

(8.7)

and

$$\begin{aligned}{{\varvec{U}}}(t)={{\varvec{U}}}(t+\phi \Delta t) -\frac{d{{\varvec{U}}}}{d t}|_{t+\phi \Delta t}\phi \Delta t+ \frac{1}{2} \frac{d ^2{{\varvec{U}}}}{d t^2}|_{t+\phi \Delta t}\phi ^2(\Delta t)^2+{\mathcal{O}}((\Delta t)^3). \end{aligned}$$

(8.8)

Subtracting the two expressions yields

$$\begin{aligned} \frac{{{\varvec{U}}}(t+\Delta t)-{{\varvec{U}}}(t)}{\Delta t}={{\varvec{V}}}(t+\phi \Delta t)+\hat{\mathcal{O}}(\Delta t). \end{aligned}$$

(8.9)

Inserting Eq. 8.6 yields

$$\begin{aligned}{{\varvec{U}}}(t+\Delta t)={{\varvec{U}}}(t)+\left( \phi{{\varvec{V}}}(t+\Delta t)+(1-\phi ){{\varvec{V}}}(t)\right) \Delta t +\hat{\mathcal{O}}((\Delta t)^2). \end{aligned}$$

(8.10)

and thus using Eq. 8.5 yields

$$\begin{aligned}{{\varvec{U}}}(t+\Delta t)={{\varvec{U}}}(t)+{{\varvec{V}}}(t)\Delta t+\phi (\Delta t)^2\varvec{\Psi }({{\varvec{U}}}(t+\phi \Delta t))+\hat{\mathcal{O}}((\Delta t)^2). \end{aligned}$$

(8.11)

The term $\varvec{\Psi }({{\varvec{U}}}(t+\phi \Delta t))$ can be handled in two main ways:

• $\varvec{\Psi }(t+\phi \Delta t)\approx \varvec{\Psi }(\phi{{\varvec{U}}}(t+\Delta t)+(1-\phi ){{\varvec{U}}}(t))$ or

• $\varvec{\Psi }(t+\phi \Delta t)\approx \phi \varvec{\Psi }({{\varvec{U}}}(t+\Delta t))+(1-\phi )\varvec{\Psi }({{\varvec{U}}}(t))$.

The differences are quite minute between either of the above, thus, for brevity, we choose the latter. In summary, we have the following:

$$\begin{aligned}{{\varvec{U}}}(t+\Delta t)={{\varvec{U}}}(t)+{{\varvec{V}}}(t)\Delta t+\phi (\Delta t)^2\left( \phi \varvec{\Psi }({{\varvec{U}}}(t+\Delta t))+(1-\phi )\varvec{\Psi }({{\varvec{U}}}(t))\right) +\hat{\mathcal{O}}((\Delta t)^2). \end{aligned}$$

(8.12)

We note that

• When $\phi =1$, then this is the (implicit) Backward Euler scheme, which is very stable (very dissipative) and ${\mathcal{O}}((\Delta t)^2)$ locally in time,

• When $\phi =0$, then this is the (explicit) Forward Euler scheme, which is conditionally stable and ${\mathcal{O}}((\Delta t)^2)$ locally in time,

• When $\phi =0.5$, then this is the (implicit) “Midpoint” scheme, which is stable and $\hat{\mathcal{O}}((\Delta t)^2)={\mathcal{O}}((\Delta t)^3)$ locally in time.

In summary, we have for the velocity¹⁰

$$\begin{aligned}{{\varvec{V}}}(t+\Delta t)={{\varvec{V}}}(t)+\Delta t \left( \phi \varvec{\Psi }({{\varvec{U}}}(t+\Delta t)) +(1-\phi )\varvec{\Psi }({{\varvec{U}}}(t))\right) \end{aligned}$$

(8.13)

and for the position

$$\begin{aligned}{{\varvec{U}}}(t+\Delta t)&{}={{\varvec{U}}}(t)+{{\varvec{V}}}(t+\phi \Delta t)\Delta t \nonumber \\= &{}{{\varvec{U}}}(t)+\left( \phi{{\varvec{V}}}(t+\Delta t)+(1-\phi ){{\varvec{V}}}(t)\right) \Delta t, \end{aligned}$$

(8.14)

or more explicitly

$$\begin{aligned}{{\varvec{U}}}(t+\Delta t)={{\varvec{U}}}(t)+{{\varvec{V}}}(t)\Delta t +\phi (\Delta t)^2 \left( \phi \varvec{\Psi }({{\varvec{U}}}(t+\Delta t))+(1-\phi )\varvec{\Psi }({{\varvec{U}}}(t))\right) . \end{aligned}$$

(8.15)

In iterative (recursion) form

$$\begin{aligned}{{\varvec{U}}}^{L+1,K}=\underbrace{(\phi \Delta t)^2\varvec{\Psi }({{\varvec{U}}}^{L+1,K-1})}_{{\mathcal{G}}({{\varvec{U}}}^{L+1,K-1})}+ \underbrace{{{\varvec{U}}}^L+{{\varvec{V}}}^L\Delta t+(\Delta t)^2\phi (1-\phi )\varvec{\Psi }({{\varvec{U}}}^L)}_{{\mathcal{R}}} \end{aligned}$$

(8.16)

Remark

Applying this scheme to the balance of linear momentum continuum formulation, under infinitesimal deformations, $\nabla _X \cdot \varvec{\sigma }+{{\varvec{f}}}=\rho \frac{\partial ^2{{\varvec{u}}}}{\partial t^2}$ we use $\varvec{\Psi }({{\varvec{u}}}(t))=\frac{\nabla _X\cdot \varvec{\sigma }+{{\varvec{f}}}}{\rho }$, and must apply the (iterative) process introduced earlier to all nodes in the system.