A practical solution in delineating thin conducting structures and suppression problem in direct current resistivity sounding

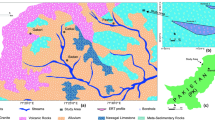
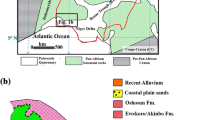
In hard rock areas, conventional apparent resistivity measurement using Schlumberger resistivity sounding fails to detect thin conducting structures (2-D and 3-D fractures filled with groundwater and mineral aggregate) concealed at a large depth. In the present study, an attempt is made to way-out the detection problem of deep seated thin conducting layer. It is proposed to study the apparent conductance simultaneously with resistivity sounding to detect such conductive zones qualitatively. Apparent conductance is defined as the magnitude of current flowing in the subsurface for a unit applied voltage through current electrodes. Even though such measurement is of qualitative importance, it gives extremely valuable information for the presence of conductive zones at depth in challenging hard rock terrain. It has been observed that apparent conductance increases significantly when groundwater bearing fractures and conductive bodies are encountered in the subsurface. Field data from different locations are presented to demonstrate the efficacy of such measurement. The measurement assists to the conventional resistivity sounding for successful prediction of groundwater zones at large depth in different hard rock areas and is of enormous importance. The approach is also used for possible solution of suppression problem in the DC resistivity sounding when intermediate layer is not reflected in the resistivity sounding curve. Finally, the approach can be used together with resistivity sounding to solve many practical problems.

Appendix 1

1.1 Theoretical formulations of horizontal current density

Over a multilayered earth, the general solution for potential in the ith layer (V _i ) at any point (r, z) due to a point current source (I) placed on the earth surface is given by Bhattacharya and Patra (1968).

$$\begin{array}{lll} \label{eq2} V_i \left({r,z} \right)\!\!\!&=&\!\!\!\frac{I\rho_1 }{2\pi }\frac{1}{\left( {r^2+z^2} \right)^{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}+\int\limits_0^\infty \left\{A_i \left( m \right)e^{-mz}\right.\\[6pt] &&\left.+\,B_i \left( {m} \right)e^{mz}\right\}J_0 \left( {mr} \right)dm. \end{array} $$

(1)

The coefficients A _i and B _i can be determined from the boundary conditions. The boundary conditions to be satisfied at any boundary are:

$$ \label{eq3} V_i =V_{i+1} $$

(2)

and

$$ \label{eq4} \frac{1}{\rho_i }\frac{\partial V_i }{\partial z}=\frac{1}{\rho_{i+1} }\frac{\partial V_{i+1} }{\partial z}\quad \mbox{at}\,z=H_i $$

(3)

H _i is the depth of the ith interface from surface and ρ _i is the resistivity of the ith layer. It has been shown by Bhattacharya and Patra (1968) that coefficient A ₁ = B ₁ and B _n  = 0. There are equal number of unknowns and equations hence all the coefficients A _i and B _i can be solved uniquely for n-layer structure.

For a three-layer case, following four equations can be written for two interfaces.

$$ \label{eq5} A_1\! \left( {e^{-mH_1 }\!+\!e^{mH_1 }} \right)\!-\!A_2 e^{-mH_1 }\!-\!B_2 e^{mH_1 }\!=\!0 $$

(4)

$$\begin{array}{lll}\label{eq6} && A_1 \rho_2\! \left( {-e^{-mH_1 }+e^{mH_1 }} \right)+A_2 \rho_1 e^{-mH_1 }\\[3pt] && \qquad -\,B_2 \rho_1 e^{mH_1 }-q\left( {\rho_2 -\rho_1 } \right)e^{-mH_1 }=0 \end{array} $$

(5)

$$ \label{eq7} A_2 e^{-mH_2 }+B_2 e^{mH_2 }-A_3 e^{-mH_2 }=0 $$

(6)

$$\begin{array}{lll}\label{eq8} && -A_2 \rho_3 e^{-mH_2 }+B_2 \rho_3 e^{mH_2 }+A_3 \rho_2 e^{-mH_2 }\\[5pt] &&\qquad -\,q\left( {\rho_3 -\rho_2 } \right)e^{-mH_2 }=0 \end{array} $$

(7)

In equations (5) and (7), q is given by the relation q = (ρ ₁ I/2π).

Since D.C. resistivity method deals with potential measurement at the earth’s surface, therefore, solution of coefficient A ₁ is sufficient. Solution for potential on the earth surface can be written in terms of resistivity transform and apparent resistivity can be computed using digital linear filtering (Ghosh 1971; Koefoed 1979). This can also be found in standard text book dealing with electrical methods. However, computation of potential at any point inside the earth and subsequent derivation of current density in various layers requires the solution of all coefficients (A _i and B _i ).

For, a 3-layer case, solution for the four coefficients is derived by solving equations (4) to (7).

$$ \label{eq9} A_1 =q\frac{K_{12} g^{p_1 }+K_{23} g^{p_2 }}{1-K_{12} g^{p_1 }-K_{23} g^{p_2 }+K_{12} K_{23} g^{p_2 -p_1 }} $$

(8)

$$ \label{eq10} A_2 =q\frac{K_{12} g^{p_1 }+K_{23} g^{p_2 }-K_{12} K_{23} g^{p_2 -p_1 }+K_{12} }{1-K_{12} g^{p_1 }-K_{23} g^{p_2 }+K_{12} K_{23} g^{p_2 -p_1 }} $$

(9)

$$ \label{eq11} B_2 =q\frac{K_{23} \left( {K_{12} +1} \right)g^{p_2 }}{1-K_{12} g^{p_1 }-K_{23} g^{p_2 }+K_{12} K_{23} g^{p_2 -p_1 }} $$

(10)

$$\label{eq12} A_3 =q\frac{K_{12} g^{p_1} + K_{23} g^{p_2} - K_{12} K_{23} g^{p_2 - p_1} + K_{12} + K_{23} + K_{12} K_{23}}{1-K_{12} g^{p_1}-K_{23} g^{p_2} + K_{12} K_{23} g^{p_2 - p_1}} $$

(11)

In equations (8–11), K _ij  = (ρ _j  − ρ _i )/(ρ _j  + ρ _i ), $e^{-2mH_{0}}=g$ and p ₁, p ₂ are whole numbers such that p ₁ = H ₁/H ₀, p ₂ = H ₂/H ₀ (H ₀ has some fixed value). Since p ₁ and p ₂ are whole numbers, A ₁ is rational function of g, therefore, we can write:

$$ \label{eq13} A_1 =q\left( {b_1 g+b_2 g^2+b_3 g^3+\cdots} \right)=q\sum\limits_{n=1}^\infty {b_n } g^n $$

(12)

Since, coefficients of any order of g must be identical in both expressions (equations 8 and 12), the coefficients b _n can be obtained by equating the coefficients of g ⁿ in the above two equations. Similarly A ₂, B ₂ and A ₃ are obtained. Let

$$ \label{eq14} A_2 =q\sum\limits_{n=0}^\infty {c_n } g^n, $$

(13)

$$ \label{eq15} B_2 =q\sum\limits_{n=1}^\infty {d_n } g^n, $$

(14)

$$ \label{eq16} A_3 =q\sum\limits_{n=0}^\infty {e_n } g^n. $$

(15)

Thus the potential at any point in different layers, due to a single electrode on the surface can be written as:

$$\begin{array}{lll}\label{eq17} V_1 &=&\frac{I\rho_1 }{2\pi }\Bigg[\frac{1}{\sqrt {r^2+z^2} }+\sum\limits_{n=1}^\infty \frac{b_n }{\sqrt {r^2+\left( {2nH_0+z} \right)^2} }\\ && +\sum\limits_{n=1}^\infty {\frac{b_n}{\sqrt {r^2+\left( {2nH_0 -z} \right)^2}}} \Bigg], \end{array}$$

(16)

$$\begin{array}{lll}\label{eq18} V_2 &=&\frac{I\rho_1 }{2\pi }\Bigg[\frac{1}{\sqrt {r^2+z^2} }+\sum\limits_{n=0}^\infty \frac{c_n }{\sqrt {r^2+\left( {2nH_0 +z} \right)^2} }\\ && +\sum\limits_{n=1}^\infty {\frac{d_n }{\sqrt {r^2+\left( {2nH_0 -z} \right)^2} }}\Bigg], \end{array}$$

(17)

$$ \label{eq19} V_3 = \frac{I\rho_1 }{2\pi }\left[ {\frac{1}{\sqrt {r^2+z^2} }+\sum\limits_{n=0}^\infty {\frac{e_n }{\sqrt {r^2+\left( {2nH_0 +z} \right)^2} }} } \right]. $$

(18)

The potential at any point in different layers, due to two electrodes placed at a distance L apart on the surface can be written as:

$$ \label{eq20} V_1 =\frac{I\rho_1 }{2\pi }\left[ {\begin{array}{l} \frac{1}{\sqrt {r_1^2+z^2} }+\sum\limits_{n=1}^\infty {\frac{b_n }{\sqrt {r_1^2+\left( {2nH_0 +z} \right)^2} }+\sum\limits_{n=1}^\infty {\frac{b_n }{\sqrt {r_1^2+\left( {2nH_0 -z} \right)^2} }-} } \frac{1}{\sqrt {r_2 ^2+z^2} } \\ -\sum\limits_{n=1}^\infty {\frac{b_n }{\sqrt {r_2^2+\left( {2nH_0 +z} \right)^2} }-\sum\limits_{n=1}^\infty {\frac{b_n }{\sqrt {r_2^2+\left( {2nH_0 -z} \right)^2} }} } \\ \end{array}} \right] $$

(19)

$$ \label{eq21} V_2 =\frac{I\rho_1 }{2\pi }\left[ {\begin{array}{l} \frac{1}{\sqrt {r_1^2+z^2} }+\sum\limits_{n=0}^\infty {\frac{c_n }{\sqrt {r_1^2+\left( {2nH_0 +z} \right)^2} }+\sum\limits_{n=1}^\infty {\frac{d_n }{\sqrt {r_1^2+\left( {2nH_0 -z} \right)^2} }-} } \frac{1}{\sqrt {r_2 ^2+z^2} } \\ -\sum\limits_{n=0}^\infty {\frac{c_n }{\sqrt {r_2^2+\left( {2nH_0 +z} \right)^2} }-\sum\limits_{n=1}^\infty {\frac{d_n }{\sqrt {r_2^2+\left( {2nH_0 -z} \right)^2} }} } \\ \end{array}} \right] $$

(20)

$$\begin{array}{lll}\label{eq22} V_3 &=& \frac{I\rho_1 }{2\pi }\Bigg[\frac{1}{\sqrt {r_1^2+z^2} }+\sum\limits_{n=0}^\infty \frac{e_n }{\sqrt {r_1^2+\left( {2nH_0 +z} \right)^2}}\\ && -\frac{1}{\sqrt {r_2^2+z^2}}-\sum\limits_{n=0}^\infty {\frac{e_n}{\sqrt{r_2^2+\left({2nH_0 +z}\right)^2}}}\Bigg]\\ \end{array} $$

(21)

where r ₁ and r ₂ are distances from the first and second electrodes, respectively.

The horizontal current density j _x at a point is given by:

$$ \label{eq23} j_x =-\frac{1}{\rho }\frac{\partial V}{\partial x}. $$

(22)

Thus the horizontal current densities in different layers at a depth z and L/2 units from each electrode can be obtained as:

$$\begin{array}{lll}\label{eq24} j_x &=& \frac{I}{2\pi}\!\left[\frac{L}{\left({\frac{L^2}{4}+z^2} \right)^{3/2}}\!+\!\sum\limits_{n=1}^\infty \frac{b_n L}{\left( {\frac{L^2}{4}\!+\!\left( {2nH_0 \!+\! z} \right)^2} \right)^{3/2}}\right.\\[15pt] && \left. +\,\sum\limits_{n=1}^\infty {\frac{b_n L}{\left( {\frac{L^2}{4}+\left( {2nH_0 -z} \right)^2} \right)^{3/2}}} \right]\quad \mbox{for}\,\,{z} \leq{H}_1\\ \end{array} $$

(23)

$$\begin{array}{lll}\label{eq25} j_x \! &=&\! \frac{I\rho_1 }{2\pi \rho_2 }\!\!\left[\! \frac{L}{\left( {\frac{L^2}{4}\!+\!z^2} \right)^{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}\!+\!\sum\limits_{n=0}^\infty \frac{c_n L}{\left( {\frac{L^2}{4}\!+\!\left( {2nH_0 +z} \right)^2} \right)^{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}\!\!\!\!\!\!\!\!\!\!\right.\\ && \left. +\sum\limits_{n=1}^\infty {\frac{d_n L}{\left( {\frac{L^2}{4}\!+\!\left( {2nH_0 \!-\! z} \right)^2} \right)^{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}} \!\right]\quad \mbox{for}\,{H}_1 \!<\!{z}\!\le\! {H}_2\\ \end{array} $$

(24)

$$\begin{array}{lll} \label{eq26} j_x\!\!\!\! &=&\!\!\!\!\frac{I\rho_1 }{2\pi \rho_3 }\left[ \frac{L}{\left( {\frac{L^2}{4}+z^2} \right)^{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}\right.\\[12pt] &&{\kern-.85pc}\left.+\sum\limits_{n=0}^\infty {\frac{e_n L}{\left( {\frac{L^2}{4}\!+\!\left( {2nH_0 \!+\! z} \right)^2} \right)^{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}}}\right]\quad \mbox{for}\,{z}\!>\!{H}_2.\\ \end{array} $$

(25)

Current density over homogeneous half-space is given by the first term of equation (23) and it is independent on the resistivity of the medium (Telford et al. 1990). Current density computed over 3-layered earth will be compared with current density in homogeneous half-space to demonstrate the increase in current flow when a conducting layer will encounter at depth. A three-layer model is depicted by putting a 10 Ωm layer at 100 m depth in a 250 Ωm homogeneous half-space. Hence the model resistivities are 250, 10, 250 Ωm and thickness of top layer 100 m with variable second layer thickness 2, 5 and 10 m.

Variation of current density with depths (0–200 m) for different current electrode separations (20, 50, 100, 150, 200, and 500 m) over 3-layer model mentioned above are presented in figure A1. Current density is higher at shallower depth for smaller current electrode separations and then gradually decreases with the increase of current electrode separation. Current density in the intermediate conducting layer is very small at smaller electrode separation (L = 20 m in figure A1) and it increases gradually with the increase in current electrode separation. It becomes maximum at a given current electrode separation and then decreases with the increase in the current electrode separation. Variation of current density for different thickness of the conducting layer is also shown in figure A1. It is observed that the magnitude of current density is more for a thin layer (2 m) compared to a thick layer (10 m).

Figure A1

Variation of horizontal current density with depth for different current electrode separation.

In this section, mathematically it has been shown that current density will not be always maximum at the surface. Instead it will be greater at depth when a conducting layer encounter at depth. In such situation, current flow will increase for larger current electrode separations.