Skip to main content
SpringerLink
Log in

Global Mittag–Leffler stability of complex valued fractional-order neural network with discrete and distributed delays

  • Published:
Rendiconti del Circolo Matematico di Palermo Series 2 Aims and scope Submit manuscript

Abstract

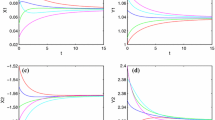
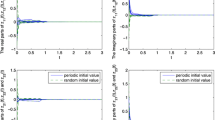
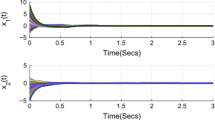
Fractional-order Hopfield neural network are often used to model the processing of information on the basis of interaction among the neurons. To show the constancy of the processed information, the system needs to be stable. In this paper, we deal with the problem of existence and uniform stability analysis of a complex valued fractional order delayed neural network. Moreover, as an extension to real valued neural network, this paper provides sufficient conditions for Mittag–Leffler stability of the system. At the end, we give three suitable examples to substantiate the effectiveness of the obtained theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Hopfield, J.: Neurons with graded response have collective computational properties like those of two-state neurons. Proc. Natl. Acad. Sci. USA Biophys. 81(10), 3088–3092 (1984)

    Article  Google Scholar 

  2. Abbas, S., Erturk, V.S., Momani, S.: Dynamical analysis of the Irving–Mullineux oscillator equation of fractional order. Signal Process. 102, 171–176 (2014)

    Article  Google Scholar 

  3. Abbas, S., Mahto, L., Favini, A., Hafayed, M.: Dynamical study of fractional model of allelopathic stimulatory phytoplankton species. Differ. Equ. Dyn. Syst., 1–14 (2014)

  4. Abbas, S.: Existence of solutions to fractional order ordinary and delay differential equations and applications. Electron. J. Differ. Equ. 9, 1–11 (2011)

    MathSciNet  Google Scholar 

  5. Abbas, S., Banerjee, M., Momani, S.: Dynamical analysis of fractional-order modified logistic model. Comput. Math. Appl. 62(3), 1098–1104 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  6. El Raheem, Z.F., Salman, S.M.: On a discretization process of fractional-order logistic differential equation. J. Egypt. Math. Soc. 22(3), 407–412 (2014)

  7. Agarwal, R.P., El-Sayed, A.M.A., Salman, S.M.: Fractional-order Chua’s system: discretization, bifurcation and chaos. Adv. Differ. Equ. 2013(1), 320 (2013)

    Article  MathSciNet  Google Scholar 

  8. Hirsch, M.W., Smale, S.: Differential Equations, Dynamical Systems, and Linear Algebra. Pure and Applied Mathematics, vol. 60, 358 p. Academic Press, New York, London (1974)

  9. Hartley, T.T., Lorenzo, C.F., Qammer, H.K.: Chaos in a fractional order Chua’s system. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 42(8), 485–490 (1995)

    Article  Google Scholar 

  10. Kaslik, E., Sivasundaram, S.: Dynamics of fractional-order neural networks. The 2011 International Joint Conference on Neural Networks (IJCNN), IEEE (2011)

  11. Lundstrom, B.N., Higgs, M.H., Spain, W.J., Fairhall, A.L.: Fractional differentiation by neocortical pyramidal neurons. Nat. Neurosci. 11(11), 1335–1342 (2008)

    Article  Google Scholar 

  12. Caputo, M., Mainardi, F.: A new dissipation model based on memory mechanism. Pure Appl. Geophys. 91(1), 134–147 (1971)

    Article  MathSciNet  MATH  Google Scholar 

  13. Çelik, V., Demir, Y.: Chaotic Fractional Order Delayed Cellular Neural Network, New Trends in Nanotechnology and Fractional Calculus Applications. Springer, The Netherlands (2010)

    MATH  Google Scholar 

  14. Kaslik, E., Sivasundaram, S.: Nonlinear dynamics and chaos in fractional-order neural networks. Neural Netw. 32, 245–256 (2012)

    Article  MATH  Google Scholar 

  15. Zou, T., Qu, J., Chen, L., Yang, Z.: Stability analysis of a class of fractional-order neural networks. Indones. J. Electr. Eng. 12(2), 1086–1093 (2014)

    Google Scholar 

  16. Chen, L., Chai, Y., Wu, R., Ma, T., Zhai, H.: Dynamic analysis of a class of fractional-order neural networks with delay. Neurocomputing 111, 190–194 (2013)

    Article  Google Scholar 

  17. Wang, H., Yu, Y., Wen, G.: Stability analysis of fractional-order Hopfield neural networks with time delays. Neural Netw. 55, 98–109 (2014)

    Article  MATH  Google Scholar 

  18. Sierociuk, D., Grzegorz, S., Andrzej, D.: Discrete fractional order artificial neural network. Acta Mech. Autom. 5, 128–132 (2011)

    Google Scholar 

  19. Hirsch, M.W.: Convergent activation dynamics in continuous time networks. Neural Netw. 2(5), 331–349 (1989)

    Article  Google Scholar 

  20. Alofi, A., Cao, J., Elaiw, A., Al-Mazrooei, A.: Delay-dependent stability criterion of caputo fractional neural networks with distributed delay. Discrete Dyn. Nat. Soc., Article ID 529358 (2014)

  21. Momani, S., Hadid, S.B.: An algorithm for numerical solutions of fractional order differential equations. J. Fract. Calculus 15, 61–66 (1999)

    MathSciNet  MATH  Google Scholar 

  22. Jin, H., Wang, J.: Global stability of complex-valued recurrent neural networks with time-delays. IEEE Trans. Neural Netw. Learn. Syst. 23(6), 853–865 (2012)

    Article  Google Scholar 

  23. Hirose, A.: Complex-Valued Neural Networks: Theories and Applications. World Scientific, Singapore (2003)

    Book  MATH  Google Scholar 

  24. Bohner, M., Rao, V.S.H., Sanyal, S.: Global stability of complex-valued neural networks on time scales. Differ. Equ. Dyn. Syst. 19(1–2), 3–11 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  25. Barron, A.R.: Universal approximation bounds for superpositions of a sigmoidal function. IEEE Trans. Inf. Theory 39(3), 930–945 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  26. Chen, Z., Cao, F.: The approximation operators with sigmoidal functions. Comput. Math. Appl. 58(4), 758–765 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  27. Costarelli, D., Spigler, R.: Solving Volterra integral equations of the second kind by sigmoidal functions approximation. J. Integr. Equ. Appl. 25(2), 193–222 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  28. Costarelli, D., Spigler, R.: A collocation method for solving nonlinear Volterra integro-differential equations of neutral type by sigmoidal functions. J. Integr. Equ. Appl. 26(1), 15–52 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  29. Costarelli, D., Spigler, R.: Approximation by series of sigmoidal functions with applications to neural networks. Annali di Matematica Pura ed Applicata 194(1), 289–306 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  30. Cybenko, G.: Approximation by superpositions of a sigmoidal function. Math. Control Signals Syst. 2(4), 303–314 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  31. Iliev, A.I., Kyurkchiev, N., Markov, S.: On the approximation of the cut and step functions by logistic and Gompertz functions. Biomath 4(2), Article-ID 1510101 (2015)

  32. Kyurkchiev, N., Markov, S.: Sigmoid Functions: Some Approximation and Modelling Aspects. Some Moduli in Programming Environment Mathematica. Lambert Acad. Publ. (2015)

  33. Lewicki, G., Marino, G.: Approximation by superpositions of a sigmoidal function. Zeitschrift für Analysis und ihre Anwendungen 22(2), 463–470 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  34. Rudin, W.: Real and Complex Analysis. McGraw-Hill, New York (1987)

    MATH  Google Scholar 

  35. Özdemir, N., İskender, B.B., Özgür, N.Y.: Complex valued neural network with Möbius activation function. Commun. Nonlinear Sci. Numer. Simul. 16(12), 4698–4703 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  36. Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations, vol. 204. Elsevier, Amsterdam (2006)

    MATH  Google Scholar 

  37. Miller, K.S., Ross, B.: An Introduction to the Fractional Calculus and Fractional Differential Equations. Wiley, New York (1993)

    MATH  Google Scholar 

  38. Podlubny, I.: Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications, vol. 198. Academic Press, New York (1998)

  39. Rakkiyappan, R., Cao, J., Velmurugan, G.: Existence and uniform stability analysis of fractional-order complex-valued neural networks with time delays. IEEE Trans. Neural Netw. Learn.Syst. 26(1), 84–97 (2015)

    Article  MathSciNet  Google Scholar 

  40. Ren, F., Cao, F., Cao, J.: Mittag–Leffler stability and generalized Mittag–Leffler stability of fractional-order gene regulatory networks. Neurocomputing 160, 185–190 (2015)

    Article  Google Scholar 

  41. Zhang, S., Yu, Y., Hu, W.: Robust stability analysis of fractional-order Hopfield neural networks with parameter uncertainties. Math. Probl. Eng. 2014, 302702-1–302702-14 (2014)

  42. Chen, J., Zeng, Z., Jiang, P.: Global Mittag–Leffler stability and synchronization of memristor-based fractional-order neural networks. Neural Netw. 51, 1–8 (2014)

    Article  MATH  Google Scholar 

  43. Stamova, I.: Global Mittag–Leffler stability and synchronization of impulsive fractional-order neural networks with time-varying delays. Nonlinear Dyn. 77(4), 1251–1260 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  44. Bhalekar, S., Daftardar-Gejji, V.: A predictor-corrector scheme for solving nonlinear delay differential equations of fractional order. J. Fract. Calculus Appl. 1(5), 1–9 (2011)

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

We are thankful to the reviewers for their constructive comments and suggestions, which helped in improving the manuscript considerably.

Author information

Authors and Affiliations

  1. School of Basic Sciences, Indian Institute of Technology, Mandi, HP, 175001, India

    Swati Tyagi & Syed Abbas

  2. Laboratory of Applied Mathematics, Biskra University, PO. Box 145, 07000, Biskra, Algeria

    Mokhtar Hafayed

Authors
  1. Swati Tyagi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Syed Abbas
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mokhtar Hafayed
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Syed Abbas.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tyagi, S., Abbas, S. & Hafayed, M. Global Mittag–Leffler stability of complex valued fractional-order neural network with discrete and distributed delays. Rend. Circ. Mat. Palermo, II. Ser 65, 485–505 (2016). https://doi.org/10.1007/s12215-016-0248-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12215-016-0248-8

Keywords

Mathematics Subject Classification

Search

Navigation