Introduction

The precipitation and deposition of crude oil polar fractions such as asphaltenes in petroleum reservoirs reduce considerably the rock permeability and the oil recovery. So, many researchers studied this important subject. They introduced experimental procedures or even analytical models, but a fully satisfactory interpretation is still lacking. The available models for description of asphaltene precipitation are divided into two general groups. The first group consists of thermodynamic models, which need asphaltene properties such as density, molecular weight and solubility parameter for prediction of asphaltene phase behavior. All those models consider asphaltene as a pure pseudo-component, but this assumption causes much deviation in the prediction of asphaltene phase behavior (Pedersen et al. 1989); the second group of models is based on the scaling approach which explained separately. In this paper, the ability of the artificial intelligence in establishing and predicting amount of asphaltene precipitation is to be investigated. Artificial intelligence have been widely used and are gaining attention in petroleum engineering because of their ability to solve problems that previously were difficult or even impossible to solve. One example of ability neural network in well-log analysis. This technique has been increasingly applied to predict reservoir properties using well-log data (Doveton and Prensky 1992; Balan et al. 1995).

A soft sensor is a conceptual device whose output or inferred variable can be modeled in terms of other parameters that are relevant to the same process (Rallo et al. 2002). According to Rallo et al. (2002), artificial neural network (ANN) could be used as soft sensor building approach.

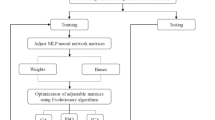
The determination of network structure and parameters is very important; some evolutionary algorithms such as genetic algorithm (GA) (Qu1 et al. 2008), back propagation (BP) (Tang and Xi 2008), pruning algorithm (Reed 1993), simulated annealing (de Souto et al. 2002) can be used for this determination. Recently, a new evolutionary algorithm has been proposed by Atashpaz-Gargari and Lucas (2007) which has inspired from a socio-political evolution, called imperialist competitive algorithm (ICA).

In the present work, we propose ICA for optimizing the weights of feed-forward neural network. Then simulation results demonstrate the effectiveness and potential of the new proposed network for asphaltene precipitation prediction compared with scaling model (Hu and Guo 2001) using the same data.

Scaling model

The three variables involved in the scaling equation are the weight percent of precipitated Asphaltenes, W (based on the weight of feed oil), the dilution ratio, R (defined as the ratio of injected solvent volume to weight of crude oil), and the molecular weight of solvent, M. Rassamdana et al. (1996) combined the three variables into two (X,Y) as follows:

$$ X = \frac{R}{{M^{Z} }} $$
(1)
$$ Y = \frac{W}{{R^{{Z^{'} }} }} $$
(2)

Z and Z′ are two adjustable parameters and must be carefully tuned to obtain the best scaling fit of the experimental data. They suggested Z′ is a universal constant of −2 and Z = 0.25 regardless of oil and precipitant used. The proposed scaling equation is expressed in terms of X and Y through a third-order polynomial function

$$ {\text{Y}} = A_{1} + A_{2} X + A_{3} X^{2} + A_{4} X^{3} \left( {X > X_{\text{c}} } \right) $$
(3)

where Xc is the value of X at the onset of asphaltene precipitation.

Hu et al. (2000) performed a detailed study on the application of scaling equation proposed by Rassamdana et al. (1996) for asphaltene precipitation. They examined the universality of exponents Z and Z′ and found that Z′ is a universal constant (Z′ = −2) while exponent Z depends on the oil composition and independent of specific precipitant (n-alkane) used. For the experimental data used, they found also that the optimum value of Z is generally within the range of 0.1 < Z < 0.5.

Despite the simplicity and accuracy of the scaling equation mentioned above, it is restricted to use at a constant temperature and since temperature is not involved in the scaling equation as a variable, it is not adequate for correlating and predicting the asphaltene precipitation data measured at different temperatures. Due to this issue, Rassamdana et al. modified their scaling equation by implanting temperature parameter in the scaling equation. Based on the previous equation, they defined two new variables x and y:

$$ x = X/T^{{C_{1} }} $$
(4)
$$ y = Y/X^{{C_{2} }} $$
(5)

in which X and Y are variables defined as in Eqs. (1) and (2) and constant C1 and C2 are adjustable parameters. They reported that the good fit of their experimental data can be achieved by setting C1 = 0.25 and C2 = 1.6.

Again the new scaling equation is a third-order polynomial in general form of:

$$ {\text{y}} = b_{1} + b_{2} {\text{x}} + b_{3} {\text{x}}^{2} + b_{4} {\text{x}}^{3} \left( {x > x_{\text{c}} } \right) $$
(6)

Hu et al. (2001) studied the effects of temperature, molecular weight of n-alkane precipitants and dilution ratio on asphaltene precipitation in a Chinese crude oil experimentally. The amounts of asphaltene precipitation at four temperatures in the range of 293–338 K were measured using seven n-alkanes as precipitants. They found that their experimental data could not be well correlated by setting C1 = 0.25 and C2 = 1.6 as recommended by Rassamdana et al. (1996). They reported that their experimental data could be correlated successfully by choosing C1 = 0.5 and C2 = 1.6. Regression plot of predicted asphaltene precipitation using scaling model (Hu and Guo 2001) against experimental data is shown in Fig. 1.

Fig. 1
figure 1

Movement of colonies toward their relevant imperialist

Full size image

Artificial neural networks

Artificial neural networks are parallel information processing methods which can express complex and nonlinear relationship use number of input–output training patterns from the experimental data. ANNs provides a non-linear mapping between inputs and outputs by its intrinsic ability (Hornik et al. 1990).

The most common neural network architecture is the feed-forward neural network. Feed-forward network is the network structure in which the information or signals will propagate only in one direction, from input to output. A three layered feed-forward neural network with back propagation algorithm can approximate any nonlinear continuous function to an arbitrary accuracy (Brown and Harris 1994; Hornick et al. 1989).

The network is trained by performing optimization of weights for each node interconnection and bias terms until the output values at the output layer neurons are as close as possible to the actual outputs. The mean squared error of the network (MSE) is defined as:

$$ {\text{MSE}} = \frac{1}{2}\mathop \sum \limits_{k = 1}^{G} \mathop \sum \limits_{j = 1}^{m} \left[ {Y_{j} (k) - T_{j} (k)} \right]^{2} $$
(7)

where m is the number of output nodes, G is the number of training samples, \( Y_{j} (k) \) is the expected output, and \( T_{j} (k) \) is the actual output. The data are split into two sets: a training data set and a validating data set. The model is produced using only the training data. The validating data are used to estimate the accuracy of the model performance.

Imperialist competitive algorithm

The ICA is a new evolutionary algorithm in the evolutionary computation field based on the human’s socio-political evolution (Atashpaz-Gargari and Lucas 2007). Like other evolutionary algorithms, the ICA starts with initial populations called countries. There are two types of countries: colony and imperialist (in optimization terminology, countries with the least cost) which together form empires. In the imperialistic competition process, imperialists try to attempt to achieve more colonies. So during the competition, the powerful imperialists will be increased in the power and the weak ones will be decreased in the power. When an empire loses all of its colonies, it is assumed to be collapsed. At the end, the most powerful imperialist will remain in the world and all the countries are colonies of this unique of this empire. In this stage, imperialist and colonies have the same position and power.

The implementation procedures of our proposed matching strategy based on ICA are described as follows.

Generating initial empire

A country formed as an array of variable values to be optimized. In a Nvar dimensional optimization problem, this array defined by:

$$ {\text{Country }} = \left[ {P_{1} ,P_{2} ,P_{3} , \ldots ,P_{{N_{\text{var}} }} } \right] $$
(8)

The cost of a country is found by evaluating the cost function \( f \):

$$ Cost = f\left( {\text{country}} \right) = f([P_{1} ,P_{2} ,P_{3} , \ldots ,P_{{N_{\text{var}} }} ]) $$
(9)

The algorithm starts with the number of initial countries (Ncountry), number of imperialist (Nimp) and number of the remaining country are colonies that each belongs to an empire (Ncol) the initial number of colonies of an empire in convenience with their powers. To divide the colonies among imperialists proportionally, the normalized cost of an imperialist is defined by:

$$ C_{n} = c_{n} - { \max }_{i} \{ c_{i} \} $$
(10)

where c n is the cost of nth imperialist and C n is its normalized cost. Having the normalized cost of all imperialist, the power of each imperialist is calculated by:

$$ P_{n} = \left| {\frac{{C_{n} }}{{\mathop \sum \nolimits_{i = 1}^{{N_{\text{imp}} }} C_{i} }}} \right| $$
(11)

In the other hand, the normalized power of an imperialist is determined by its colonies. Then, the initial number of an imperialist will be:

$$ {\text{NC}}_{n} = {\text{round}}\{ P_{n} \cdot N_{\text{col}} \} $$
(12)

where \( {\text{NC}}_{n} \) is the initial number of colonies of nth empire and Ncol is the number of all colonies. To divide the colonies among imperialists, \( {\text{NC}}_{n} \) of the colonies is selected randomly and assigned them to each imperialist. The colonies together with the imperialist form the nth empire.

Moving colonies of an empire toward the imperialist

The imperialist countries try to improve their colonies and make them a part of themselves. This fact is modeled by moving all colonies toward their relevant imperialist. Figure 1 (Atashpaz-Gargari and Lucas 2007) shows this movement. In this figure, the colony moves toward the imperialist by x (is a random variable with uniform distribution) units.

$$ x\sim U(0,\beta \times d) $$
(13)

where β is a number greater than 1 and d is the distance between a colony and an imperialist. In the moving process, a colony may reach a position with lower cost than that of its imperialist. In this case, the imperialist and the colony change their positions. Then, the algorithm will continue by the imperialist in the new position and then colonies start moving toward this position.

The total power of an empire

The total power of an empire depends on both the power of the imperialist country and the power of its colonies. This fact is modelled by defining the total cost by:

$$ {\text{TC}}_{n} = {\text{Cost}}\left( {{\text{imperialist}}_{n} } \right) + \xi {\text{mean}}\{ {\text{cost}}({\text{colonies of impire}}_{n} )\} $$
(14)

where \( {\text{TC}}_{n} \) is the total cost of then th empire, and \( {{\upxi}} \) is a positive number which is considered to be less than 1. A small value for \( {{\upxi}} \) implies that the total power of an empire to be determined by just the imperialist and increasing it will increase the role of the colonies in determining the total power of an empire. The value of 0.1 for \( {{\upxi}} \) is a proper value in most of the implementations.

Imperialistic competition

All empires try to take the possession of colonies of other empires and control them. The imperialistic competition gradually brings about a decrease in the power of weaker empires and an increase in the power of more powerful ones. This competition is modelled by just picking some (usually one) of the weakest colonies of the weakest empires and making a competition among all empires to possess this colonies.

To start the competition, first, the possession probability of each empire is found based on its total power. The normalized total cost is obtained by:

$$ {\text{NTC}}_{n} = {\text{TC}}_{n} - { \max }_{i} \{ {\text{TC}}_{i} \} $$
(15)

where, \( {\text{TC}}_{n} \) and \( {\text{NTC}}_{n} \) are the total cost and the normalized total cost of nth empire, respectively. Having the normalized total cost, the possession probability of each empire is given by:

$$ P_{{P_{n} }} = \left| {\frac{{{\text{NTC}}_{n} }}{{\mathop \sum \nolimits_{i = 1}^{{N_{\text{imp}} }} {\text{NTC}}_{i} }}} \right| $$
(16)

To divide the mentioned colonies among empires, vector P is formed as

$$ {\mathbf{P}} = \left[ {P_{{P_{1} }} ,P_{{P_{2} }} ,P_{{P_{3} }} , \ldots ,P_{{P_{{N_{\text{imp}} }} }} } \right] $$
(17)

Then the vector R with the same size as P whose elements are uniformly distributed random numbers is created,

$$ {\mathbf{R}} = \left[ {r_{1} ,r_{2} ,r_{3} , \ldots r_{{N_{\text{imp}} }} } \right] $$
(18)

Then vector D is formed by subtracting R from P

$$ {\mathbf{D}} = {\mathbf{P}} - {\mathbf{R}} = \left[ {D_{1} ,D_{2} ,D_{3} , \ldots ,D_{{N_{\text{imp}} }} } \right] $$
(19)

Referring to vector D, the mentioned colony (colonies) is handed to an empire whose relevant index in D is maximized.

Powerless empire will collapse in the imperialistic competition and their colonies will be divided among other empires. At the end, all the empires except the most powerful one will collapse and all the colonies will be under the control of this unique empire. In this stage, imperialist and colonies have the same position and power.

Results and discussion

In this study, an ANN was used to build a model to predict asphaltene precipitation using the data reported in literature (Hu and Guo 2001). The best ANN architecture was: 3-4-10-1 (3 input units, 4 hidden neurons in first layer, 10 hidden neurons in second layer, 1 output neuron). ANN model trained with back propagation network was trained by Levenberg–Marquardt using three parameters: (1) molecular weight, (2) dilution ratio, and (3) temperature as inputs. The transfer functions in hidden and output layer are sigmoid and linear, respectively. Physical and thermodynamic properties of oil used for generating experimental data by Hu and Guo (2001) are shown in Table 1.

Table 1 Compositions (mol%) and properties of the degassed Caoqiao crude oil and separator gas
Full size table

ICA is used as neural network optimization algorithm and the MSE used as a cost function in this algorithm. The goal in proposed algorithm is minimizing this cost function. Every weight in the network is initially set in the range of [−1, 1]. In these simulations, the number of imperialists and the colonies is considered 4 and 40, respectively; parameter β is set to 2. The number of training and testing data is 130 and 60, respectively.

The simulation performance of the ICA–ANN model and ANN model were evaluated on the basis of MSE and efficiency coefficient R2. Table 2 gives the MSE and R2 values for the three different models of the validation phases. Prediction of asphaltene precipitation by scaling model is shown in Fig. 2 and prediction of asphaltene precipitation in the training and test phase is shown in Fig. 3. The simulation performance of the ICA–ANN model and ANN model were evaluated on the basis of MSE and efficiency coefficient R2. Table 2 gives the MSE and R2 values for three different models of the validation phases. Training state and regression plot and performance of ICA–ANN and ANN models are shown in Figs. 4, 5, 6, 7, 8 and 9, respectively. It can be observed that the performance of ICA–ANN model is better than scaling model and ANN model.

Table 2 Comparison between the performances of ICA–ANN and scaling model
Full size table
Fig. 2
figure 2

Regression plot of prediction by scaling equation (Hu and Guo 2001)

Full size image
Fig. 3
figure 3

Comparison between measured and predicted asphaltene precipitation (ICA-ANN): a training, b test

Full size image
Fig. 4
figure 4

Training state plot of ICA-ANN

Full size image
Fig. 5
figure 5

Training state plot of ANN

Full size image
Fig. 6
figure 6

Regression plot of ICA-ANN

Full size image
Fig. 7
figure 7

Regression plot of ANN

Full size image
Fig. 8
figure 8

Performance plot of ICA-ANN

Full size image
Fig. 9
figure 9

Performance plot of ANN

Full size image

Conclusions

The idea of ICA algorithm is that each initial point of the neural network is selected by ICA and the fitness of the ICA is determined by a neural network. The experiment with experimental data reported in literature (Hu and Guo 2001) has showed that the ICA–ANN model is successfully demonstrated on prediction of asphaltene precipitation also predictive performance of the proposed model is better than that of scaling model (Hu and Guo 2001) and conventional ANN model. One problem when considering the combination of neural network and ICA for prediction of asphaltene precipitation is the determination of the optimal neural network structure. Proposed neural network structure described in this work is determined manually. A substitute method is to apply the ICA or another evolutionary algorithm for neural network structure optimization, which will be a part of our future work. The proposed asphaltene precipitation prediction model may be combined with existing asphaltene precipitation modeling softwares to speed up their performance, reduce the uncertainty and increase their prediction and modeling capabilities.