Introduction

Recently nanomaterials have encouraged the interest of the scientific researchers in physics, chemistry and engineering. These nanomaterials have special properties (mechanical, chemical, electrical, optical and electronic) resulting from their nanoscale dimensions. Because of the desirable properties (Dai et al. 1996; Bachtold et al. 2001), the nanomaterials are perceived to be the components for various nanoelectromechanical systems and nanocomposites. Some of the common examples of these nanomaterials are nanoparticles, nanowires and nanotubes (viz., carbon nanotubes, ZnO nanotubes), etc. Small scale effects and the atomic forces must be incorporated in the realistic design of the nanostructures [viz., nanoresonantors (peng et al. 2006), nanoactuators (Dubey et al. 2004), nanomachines (pennadam et al. 2004) and nano-optomechanical systems] to achieve solutions with acceptable accuracy. Both experimental and atomistic simulation results show that when the dimensions of the structures become small then the ‘size effect’ has significant role in the mechanical properties (Ruud et al. 1994). Ignoring the small scale effects in sensitive nanodesigning fields may cause completely incorrect solutions and hence improper designs. Though atomistic methods (Chowdhury et al. 2010a, b) are able to capture the small scale effects and atomic forces, these approaches are computationally prohibitive for nanostructures with large number of atoms. Thus, initially analyses have been generally carried out using classical mechanics. Extensive research over the past decade has shown that the analyses of nanostructures using classical mechanics are inadequate since these theories could not capture the small scale effect in the mechanical properties. For example, Wang and Hu (2005) showed that the decrease in phase velocities of wave propagation could not be predicted by classical beam theories when the wave number is so large that microstructure of carbon nanotubes has a significant influence on the flexural wave dispersion. Therefore, recently various efforts have been carried out to bring the scale effects within the formulation by amending the traditional classical continuum mechanics. Nonlocal elasticity theory for the first time was introduced by Eringen (1972). Recent literature shows that the nonlocal elasticity theory which includes small scale effect arising at nanoscale level is being increasingly used for reliable and quick analysis of nanostructures (Wang et al. 2008; Wang 2005; Zhang et al. 2005; Shen 2011; Lu et al. 2006; Challamel and Wang 2008) like nanobeams, nanoplates, nanorings, carbon nanotubes, graphenes, nanoswitches and microtubules. Aydogdu (2009) proposed a general nonlocal beam theory to study bending, buckling and free vibration of nanobeams. Integral equation approach has been employed by Xu (2006) to investigate the free transverse vibrations of nano-to-micron scale beams and the author found that the nonlocal effect on the natural frequencies and vibrating modes is negligible for microbeams while it plays a crucial role in nanobeams. Peddieson et al. (2003) formulated nonlocal version of Euler–Bernoulli beam theory. Authors have tried to find out numerical and analytical solutions for various types of nanobeams based on nonlocal continuum mechanics. Free vibration of Euler–Bernoulli and Timoshenko nanobeams based on nonlocal continuum mechanics has been solved analytically by Wang et al. (2007). Authors have given the frequency parameters for different scaling effect parameters and boundary conditions as Simply Supported–Simply Supported (SS), Clamped–Simply Supported (CS), Clamped–Clamped (CC) and Cantilever (CF). They have given first five mode shapes of clamped nanobeams based on nonlocal Timoshenko beam theory for various values of the scaling effect parameter. Naguleswaran (2002) presented results for transverse vibration of an Euler–Bernoulli uniform beam when it carries several particles. Civalek and Akgoz (2010) analysed free vibration of microtubules based on Euler–Bernoulli beam theory using Differential Quadrature (DQ) method. Nonlocal elasticity model has also been used to study free transverse vibration of cracked Euler–Bernoulli nanobeams by Loya et al. (2009). Investigations have also been carried out in the vibration of multiwalled carbon nanotubes. Ansari and Ramezannezhad (2011) studied nonlocal Timoshenko beam model for investigating the large amplitude vibrations of embedded multiwalled carbon nanotubes including thermal effects. Murmu and Adhikari (2010) developed an analytical method to investigate transverse vibration of double-nanobeam systems using nonlocal elasticity theory.

Earlier investigations mainly focused on the use of classical mechanics in the vibration of nanobeams, which lack the accountability of the effects arising from the small scale. Thus, analysis of nanostructures has been investigated using nonlocal elasticity theory. As such, the problems have been solved by few authors using finite element method (Eltaher et al. 2012), Chebyshev polynomials in Rayleigh–Ritz method (Mohammadi and Ghannadpour 2011), meshless method (Roque et al. 2011), etc. Earlier methods may not be straightforward to problems with complicating effects. Handling of all sets of boundary conditions is another problem to analyse. Therefore, various efforts have been carried out for finding the solution of nanobeams based on nonlocal theory. This paper mainly focuses on solving the governing differential equations of Euler–Bernoulli and Timoshenko nanobeams by an efficient way. As such Rayleigh–Ritz method with simple polynomials and orthonormal polynomials has been used in this investigation. Use of boundary characteristic orthogonal polynomials in the Rayleigh–Ritz method makes the procedure easier to handle. This is because of the fact that most of the elements of mass and stiffness matrices of the generalized Eigen value problem become either zero or one due to orthonormality of the assumed shape functions. As a result, the computations become easier and efficient. Though this method has been used in vibration of classical beams and plates (Bhat 1985; Singh and Chakraverty 1994a, b, c; Chakraverty et al. 1999; Stiharu and Bhat 1997; Chakraverty 2009), it has not yet been reported for vibration of nanobeams. It may be noted that the kinetic and potential energy expressions used in the Rayleigh–Ritz method are as such not simple as compared to classical beams and plates. This is due to the fact that governing differential equations of nanobeams should be handled considering the nonlocal theory as mentioned above.

In this paper, investigation is carried out to understand the small scale effects in the free vibration of nonlocal nanobeams based on Euler–Bernoulli and Timoshenko beam theories. The solution procedure includes the transformation of the governing equations from physical domain to computational domain using simple polynomials and boundary characteristic orthogonal polynomials in the Rayleigh–Ritz method. Results from our study in special cases are compared and are found to be in good agreement. Investigations with some new boundary conditions are also incorporated. As the mode shapes are useful for engineers to design the structures (they represent the shape that the structures will vibrate in free motion), so deflection graphs for nonlocal CC Euler–Bernoulli nanobeams with various scaling effect parameters are given.

Theoretical formulation of nonlocal Euler–Bernoulli beam theory

Based on Euler–Bernoulli beam theory, the strain–displacement relation is given by

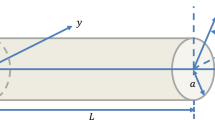
$$ \varepsilon_{xx} = - z\frac{{{\text{d}}^{2} w}}{{{\text{d}}x^{2} }} $$
(1)

where x is the longitudinal coordinate measured from the left end of the beam, \( \varepsilon_{xx} \) the normal strain, z the coordinate measured from the mid-plane of the beam and w the transverse displacement.

The strain energy \( U \) is given by

$$ U = \frac{1}{2}\int\limits_{0}^{L} {\int\limits_{A} {\sigma_{xx} } } \, \varepsilon_{xx} {\text{ d}}A{\text{d}}x $$
(2)

where \( \sigma_{xx} \) is the normal stress, L the length of the beam and A the cross-sectional area of the beam.

Substituting Eq. (1) into Eq. (2), the strain energy may be expressed as

$$ U = - \frac{1}{2}\int\limits_{0}^{L} {M\frac{{{\text{d}}^{2} w}}{{{\text{d}}x^{2} }}} {\text{d}}x $$
(3)

where M is the bending moment and is given by

$$ M = \int\limits_{A} {\sigma_{xx} \, } z{\text{d}}A $$
(4)

Assuming free harmonic motion, the kinetic energyT is given by

$$ T = \frac{1}{2}\int\limits_{0}^{L} {\rho A\omega^{2} } w^{2} {\text{d}}x $$
(5)

where \( \omega \) is the circular frequency of vibration and \( \rho \) the mass density of the beam material.

For an elastic material in one dimensional case, Eringen’s nonlocal constitutive relation may be written as (Wang et al. 2007)

$$ \sigma_{xx} - (e_{0} a)^{2} \frac{{{\text{d}}^{2} \sigma_{xx} }}{{{\text{d}}x^{2} }} = E\varepsilon_{xx} $$
(6)

where E is the Young’s modulus and \( e_{0} a \) is the scale coefficient which incorporates the small scale effect. It may be noted that a is the internal characteristic length (e.g., lattice parameter, C–C bond length and granular distance) and \( e_{0} \) is a constant, which is to be experimentally determined or approximated by matching the dispersion curves of plane waves with those of atomic lattice dynamics.

Multiplying Eq. (6) by \( Z{\text{d}}A \) and integrating over the area A yields

$$ M - (e_{0} a)^{2} \frac{{{\text{d}}^{2} M}}{{{\text{d}}x^{2} }} = - EI\frac{{{\text{d}}^{2} w}}{{{\text{d}}x^{2} }} $$
(7)

where I is the second moment of area.

The governing equation of motion (Civalek and Akgoz 2010) is given by

$$ \frac{{d^{ \, 2} M}}{{dx \, ^{2} }} = - \rho \, A \, \omega^{2} \, w $$
(8)

Substituting Eq. (8) into Eq. (7), we have

$$ M = - EI\frac{{{\text{d}}^{2} w}}{{{\text{d}}x^{2} }} - (e_{0} a)^{2} \rho A\omega^{2} w $$
(9)

Theoretical formulation of nonlocal Timoshenko beam theory

Based on the nonlocal Timoshenko beam theory, the Strain energy\( U \) is given by (Wang et al. 2007)

$$ U = \frac{1}{2}\int\limits_{0}^{L} {\int\limits_{A} {\left( {\sigma {}_{xx}\varepsilon_{xx} + \sigma_{xz} \, \gamma_{xz} } \right)} } {\text{d}}A{\text{d}}x $$
(10)

where x is the longitudinal coordinate measured from the left end of the beam, z the coordinate measured from the mid-plane of the beam,\( \sigma {}_{xx} \) the normal stress, \( \sigma_{xz} \) the transverse shear stress, \( \varepsilon_{xx} \) the normal strain, \( \gamma_{xz} \) the transverse shear strain, L the length of beam and A the cross sectional area of the beam.

The strain-displacement relations are given by

$$ \varepsilon_{xx} = z\frac{{{\text{d}}\phi }}{{{\text{d}}x}} \, $$
(11)
$$ \gamma_{xz} = \phi + \frac{{{\text{d}}w}}{{{\text{d}}x}} \, $$
(12)

where \( w \) is the transverse displacement and \( \phi \) the rotation due to bending.

Substituting Eqs. (11) and (12) into Eq. (10), the strain energy may be expressed as

$$ U = \frac{1}{2}\int\limits_{0}^{L} {\left( {M\frac{{{\text{d}}\phi }}{{{\text{d}}x}} + Q \, \left( {\phi + \frac{{{\text{d}}w}}{{{\text{d}}x}}} \right)} \right)} {\text{d}}x $$
(13)

where \( M \) and \( Q \) are the bending moment and shear force, respectively, and are given as

$$ M = \int\limits_{A} {\sigma_{xx} } z{\text{d}}A $$
$$ Q = \int\limits_{A} {\sigma_{xz} } {\text{d}}A $$

For an elastic material in one dimensional case, the nonlocal constitutive relation may be simplified as

$$ \sigma_{xx} - (e_{0} a)^{2} \frac{{{\text{d}}^{2} \sigma_{xx} }}{{{\text{d}}x^{2} }} = E\varepsilon_{xx} $$
(14)

The constitutive relation for the shear stress and strain may be written as

$$ \sigma_{xz} = G\gamma_{xz} $$
(15)

where G is the shear modulus.

Multiplying Eq. (14) by \( zdA \) and integrating the result over the area A yields

$$ M - (e_{0} a)^{2} \frac{{{\text{d}}^{2} M}}{{{\text{d}}x^{2} }} = EI\frac{{{\text{d}}\phi }}{{{\text{d}}x}} $$
(16)

where \( I \) is the second moment of area.

Also integrating Eq. (15) over the area, one may obtain

$$ Q = k_{s} {\text{GA }}\left( {\phi + \frac{{{\text{d}}w}}{{{\text{d}}x}}} \right) $$

where \( k_{s} \) is the shear correction in the Timoshenko beam theory to compensate the error in assuming a constant shear strain (stress) through the thickness of the beam.

Governing equations for the vibration behavior of Timoshenko nanobeams are given by Wang et al. (2007)

$$ \frac{{{\text{d}}M}}{{{\text{d}}x}} = Q - \rho I\omega^{2} \phi $$
(17)
$$ \frac{{{\text{d}}Q}}{{{\text{d}}x}} = - \rho A\omega^{2} w $$
(18)

where \( \rho \) is the mass density of the beam material and \( \omega \) the circular frequency of vibration.

Hence nonlocal bending moment \( M \) may be expressed as

$$ M = EI\frac{{{\text{d}}\phi }}{{{\text{d}}x}} - (e_{0} a)^{2} \left( {\rho A\omega^{2} w + \rho I\omega^{2} \frac{{{\text{d}}\phi }}{{{\text{d}}x}}} \right) $$
(19)

Assuming free harmonic motion and including the effect of rotary inertia, the kinetic energy\( T \) is given by

$$ T = \frac{1}{2}\int\limits_{0}^{L} {\left( {\rho A\omega^{2} w^{2} + \rho I\omega^{2} \phi^{2} } \right)} {\text{d}}x \, $$
(20)

Solution methodology

Using simple polynomials and orthonormal polynomials as basis functions in the Rayleigh–Ritz method, the frequency parameters for nanobeams have been computed. In this method, displacement and rotation due to bending functions are represented by a series of admissible functions.

We introduce the following nondimensional terms

\( X = \frac{x}{L},W = \frac{w}{L},\alpha = \frac{{e_{ \, 0} \, a}}{L} \) = scaling effect parameter, \( \xi = \frac{L\sqrt A }{\sqrt I } \) = slenderness ratio, \( \tau = \frac{1}{{\xi^{2} }} \), \( \lambda^{ \, 2} \, = \, \frac{{\rho \, A \, \omega^{ \, 2} \, L^{ \, 4} }}{E \, I} \) = frequency parameter and \( \Upomega \, = \, \frac{E \, I}{{k_{s} \, G \, A \, L^{ \, 2} }} \) = shear deformation parameter.

Let us assume \( W \) and \( \phi \) as

$$ W(X) = \sum\limits_{i = 1}^{n} {c_{i} } \, \varphi_{i} $$
(21)
$$ \phi (X) = \sum\limits_{i = 1}^{n} {d_{i} } \psi_{i} $$
(22)

where \( c_{i} \) and \( d_{i} \) are the unknown coefficients to be determined and n is the order of approximation to get desired accuracy. It may be noted that \( \varphi_{i} \) and \( \psi_{i} \) are admissible functions and can be represented as

$$ \phi_{i} = \eta_{b} X^{i - 1} ,\quad i = 1,2, \ldots ,n $$
$$ \psi_{i} = \eta_{b} X^{i - 1} ,\quad i = 1,2, \ldots ,n $$

where \( \eta_{b} \) is the nondimensional boundary polynomial expression for a nanobeam with varying boundary conditions and is expressed as:

$$ \eta_{b} = X^{p} (1 - X)^{q} $$
(23)

In Eq. (23), p and q take the values 0, 1 or 2 according to Free, simply supported or clamped boundary conditions, respectively. It may be noted that one may easily handle the boundary conditions of the problem by assigning various values of p and q as mentioned.

Solution for vibration of Euler–Bernoulli nanobeams

Substituting Eq. (21) into Eqs. (3) and (5) and differentiating partially with respect to unknown coefficients \( c_{j} \), a generalized Eigen value problem will be obtained as

$$ \left[ K \right]\left\{ Y \right\} = \lambda^{2} \left[ M \right]\left\{ Y \right\} $$
(24)

where \( \left\{ Y \right\} = \left[ {c_{1} c_{2} \ldots c_{n} } \right]^{T} \), and the matrices [K] and [M] are given in “Appendix”.

Solution for vibration of Timoshenko nanobeams

Again substituting Eqs. (21) and (22) into Eqs. (10) and (20) and differentiating partially with respect to the unknown coefficients \( c_{j} \) and \( d{}_{j} \), the following generalized Eigen value problem will be obtained

$$ \left[ K \right]\left\{ Y \right\} = \lambda^{2} \left[ M \right]\left\{ Y \right\} $$
(25)

where \( \left\{ Y \right\} = \left[ {c_{1} \, c_{2} \ldots c_{n} \,d_{1} d_{2} \ldots d_{n} } \right]^{T} \) and the matrices [K] and [M] are again given in “Appendix”.

Method of solution using orthonormal polynomials

Displacement and rotation due to bending functions may be expressed as

$$ W(X) = \sum\limits_{i = 1}^{n} {c_{i} \hat{\varphi }_{i} } $$
(26)
$$ \phi (X) = \sum\limits_{i = 1}^{n} {d_{i} } \hat{\psi }_{i} $$
(27)

where \( c_{i} \) and \( d_{i} \) are unknown coefficients and n is the order of approximation to get desired accuracy. It may be noted that \( \hat{\varphi }_{i} \) and \( \hat{\psi }_{i} \) are orthonormal polynomials, which may be obtained using any orthogonalisation process such as three term recurrence relation or Gram-Schmidt process. Gram-Schmidt process is used here to find orthonormal polynomials with the help of linearly independent set of functions \( \theta_{i} = \eta_{b} X^{i - 1} \), where \( \eta_{b} \) is defined as in Eq. (23). The procedure works as follows:

$$ \varphi_{1} = \theta_{1} $$
$$ \varphi_{i} = \theta_{i} - \sum\limits_{j = 1}^{i - 1} {\beta_{ij} } \varphi_{j} $$

where

$$ \beta_{ij} = \frac{{\langle \theta_{i} ,\varphi_{j} \rangle }}{{\langle \varphi_{j} ,\varphi_{j} \rangle }} $$

Here \( \langle .,.\rangle \) denotes the inner product of the functions say \( \varphi_{i} \) and \( \varphi_{j} \) and is defined as

$$ \left\langle {\varphi_{i} ,\varphi_{j} } \right\rangle = \int\limits_{0}^{1} {\varphi_{i} } (X) \, \varphi_{j} (X){\text{d}}X \, $$

The norm of the function say \( \varphi_{i} \) is given as

$$ ||\varphi_{i} || = \left\langle {\varphi_{i} ,\varphi_{i} } \right\rangle^{1/2} = \left[ {\int\limits_{0}^{1} {\varphi_{i} } (X)\varphi_{i} (X){\text{d}}X } \right]^{1/2} $$

Then the orthonormal polynomials may be obtained as

$$ \hat{\varphi }_{i} = {\raise0.7ex\hbox{${\varphi_{i} }$} \!\mathord{\left/ {\vphantom {{\varphi_{i} } {||\varphi_{i} ||}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${||\varphi_{i} ||}$}} $$

similarly \( \hat{\psi }_{i} \) may also be obtained.

Above procedure has been used here to get generalized eigen value problem as

$$ \left[ K \right]\left\{ Y \right\} = \lambda^{2} \left[ M \right]\left\{ Y \right\} $$

It may be noted that following property is satisfied due to orthonormality

$$ \left\langle {\hat{\varphi }_{i} ,\hat{\varphi }_{j} } \right\rangle = \delta_{ij} = \left\{ {\begin{array}{*{20}c} 1 & {{\text{if}}\quad i = j} \\ 0 & {{\text{if}}\quad i \ne j} \\ \end{array} \, } \right. $$

Matrices [K] and [M] are same as in Eq. (25). But due to orthonormality property in the matrix \( M \), the sub matrix \( M_{1} \) (as given in “Appendix”) will be an identity matrix. Moreover, first part of each expression for elements of matrices \( K_{4} \) and \( M_{4} \) will either be zero or one. In view of the above, the computations of the eigen value problem will reduce to a great extent.

Numerical results and discussions

Frequency parameters for single walled nanotube (SWNT) have been computed by Rayleigh–Ritz method taking simple polynomials as well as orthonormal polynomials. Different boundary polynomial expressions are considered to handle various boundary conditions at the edges. In the numerical evaluations, following material and geometrical parameters of SWNT have been used: rod diameter, d = 0.678 nm; length of beam, L = 10d; thickness of tube, t = 0.066; shear correction factor, \( k_{s} \) = 0.563; Young’s modulus, E = 5.5 TPa; shear modulus, G = E/[2(1 + v)]; Poisson’s ratio ν = 0.19 and second moment of area I = πd4/64.

In this study, frequency parameters of both Euler–Bernoulli and Timoshenko nanobeams are computed. The results are investigated for different scaling effect parameters and boundary conditions. Firstly, the frequency parameters are computed taking simple polynomials of the form \( X^{i - 1} \) in the Rayleigh–Ritz method. Then the polynomials are orthonormalised by Gram-Schmidt process and are used in the Rayleigh–Ritz method to obtain frequency parameters. Table 1 shows the convergence studies of first three frequency parameters (\( \sqrt \lambda \)) for SS and CS Euler–Bernoulli nanobeams taking \( \alpha = 0.5 \) and \( L = 10d \). Similarly convergence studies of first three frequency parameters for SS and CS Timoshenko nanobeams are tabulated in Table 2 for \( \alpha = 0.5 \) and \( L = 10d. \) In these tables, it is observed that the frequency parameters are close to the results of Wang et al. (2007) as the value of n increases. In Table 3, first four frequency parameters of Euler–Bernoulli nanobeams are presented for different end conditions and scaling effect parameters. Present results are compared with results of Wang et al. (2007) and are found to be in good agreement. Frequency parameters for local Euler–Bernoulli nanobeams are also incorporated in this table. Similarly the results of Timoshenko nanobeams subjected to various boundary conditions are given in Table 4 for different scaling effect parameters. Again the results of Wang et al. (2007) are considered for comparison of obtained frequency parameters of Timoshenko nanobeams. From Tables (3) and (4), it can be clearly seen that the nonlocal results are smaller than the corresponding local ones. Frequency parameters for Free–Free (FF) and Simply Supported–Free (SF) are also given in Table 5 for different scaling effect parameters. It may be noted that the frequency parameters obtained using orthonormalised polynomials are same as that of using simple polynomials. But here the computations become more efficient and less time is required for the execution of the program. It is due to the fact (as pointed out earlier also) that the matrix elements containing \( \hat{\varphi }_{i} \) and \( \hat{\varphi }_{j} \) become zero for i not equal to j and 1 for i equal to j due to the orthonormality. One of the interesting facts in this analysis is that CC nanobeams have highest frequency parameters than other boundary conditions. It helps the design engineers to obtain desired frequency parameters as per the application.

Table 1 Convergence of first three frequency parameters for Euler–Bernoulli nanobeams with α = 0.5 and L/d = 10 (SS and CS)
Full size table
Table 2 Convergence of first three frequency parameters for Timoshenko nanobeams with α = 0.5 and L/d = 10 (SS and CS)
Full size table
Table 3 First four frequency parameters of Euler–Bernoulli nanobeams for different scaling effect parameters and boundary conditions (SS, CS and CC)
Full size table
Table 4 First four frequency parameters of Timoshenko nanobeams for different scaling effect parameters and boundary conditions (SS, CS and CC)
Full size table
Table 5 First four frequency parameters of Timoshenko nanobeams for different scaling effect parameters and some new boundary conditions (Simply supported–Free and Free–Free)
Full size table

The behavior of the scaling effect parameter on the frequency parameter is shown in Fig. 1 for SS, CS and CC Euler–Bernoulli nanobeams. Figure 2 shows the variation in the frequency parameter with the scaling effect parameter for SS, CS and CC Timoshenko nanobeams. In these figures, first four frequency parameters are shown for both Euler–Bernoulli and Timoshenko nanobeams. Figures 1 and 2 depict that frequency parameters are over predicted, when local beam model is considered for vibration analysis of nanobeams. As the scaling effect parameter increases, the frequency parameters for nonlocal nanobeams become smaller than those of its local counterpart. This reduction can be clearly seen when we consider higher vibration modes. The reduction is due to the fact that the nonlocal model may be viewed as atoms linked by elastic springs while in case of local continuum model, the spring constant is assumed to take an infinite value. So small scale effect makes the nanobeams more flexible and nonlocal impact cannot be neglected. As such, nonlocal theory should be used for better predictions of high natural frequency of micro and nanobeams. Mode shapes are useful for engineers to design the structures, because they represent the shape that the structures will vibrate in free motion. Sometimes, the knowledge of higher modes is necessary before finalizing the design of an engineering system. Thus, while studying vibration problems viz. beam, plate or shell, one may always see the tabulation of the higher frequencies in the open literature. As such, the present investigators have reported first few higher modes in Fig. 3 for benchmarking the results, which may help the researchers of nanotechnology. In Fig. 3, we have given first five deflections of nonlocal CC Euler–Bernoulli nanobeams with scaling effect parameters as 0, 0.3 and 0.6. It can be seen that mode shapes are affected by the effect of small length scale. By understanding the modes of vibration, we can better design the structures as per the need.

Fig. 1
figure 1

Variation of small scale effect on the frequency parameter for Euler–Bernoulli nanobeams with L/d = 10. a Simply Supported–Simply Supported, b Clamped–Simply Supported, c Clamped–Clamped

Full size image
Fig. 2
figure 2

Variation of small scale effect on the frequency parameter for Timoshenko nanobeams with L/d = 10. a Simply Supported–Simply Supported, b Clamped–Simply Supported, c Clamped–Clamped

Full size image
Fig. 3
figure 3

First five deflection shapes of Clamped–Clamped nanobeams based on nonlocal Euler–Bernoulli beam model with scaling effect parameters as 0, 0.3 and 0.5. a First deflection, b Second deflection, c Third deflection, d Fourth deflection, and e Fifth deflection

Full size image

Conclusions

In this paper, an efficient numerical method is developed for free vibration of Euler–Bernoulli and Timoshenko nanobeams based on Eringen’s nonlocal elasticity theory. Small scale effect, transverse shear deformation and rotary inertia are taken into consideration in nonlocal Timoshenko beam theory, which play a vital role while dealing with micro/nanobeams that are short, stubby and especially when the frequencies are high. Vibration characteristics of Euler–Bernoulli and Timoshenko nanobeams have been computed using simple polynomials and orthonormal polynomials in the Rayleigh–Ritz method. Results for different scaling effect parameters and boundary conditions are given in tables. Convergence studies of both Euler–Bernoulli and Timoshenko nanobeams are reported for SS and CS boundary conditions taking scaling effect parameter as 0.5. Variations of frequency parameters with scaling effect parameters are shown in figures. Results are also tabulated for some new boundary conditions (SF and FF). Present results are compared with that of Wang et al. (2007) and it is observed that there is an excellence agreement. Deflection graphs of nonlocal CC Euler–Bernoulli nanobeams are plotted for different scaling effect parameters. Numerical solutions presented herein may be useful to design engineers in microelectromechanical and nanoelectromechanical devices. From this analysis, it may be concluded that the solutions obtained by the proposed method may easily be extended to various other complicated nanodomains.