Introduction and literature review

In most classical supply chain (SC) network designs, the major goal is to produce and send products from one echelon to another echelon to satisfy the demands of the market place in order to minimize the chains’ costs or maximize the total benefit. Today’s competitive market makes the supply chain management more important. Nowadays, to survive in a highly competitive market place, companies have to reduce supply chain risk, improve the distribution methods, optimize inventory levels and improve customer service and customer satisfaction. In the literature of supply chain network design problems, to make the models more realistic, several objectives are considered together (Murillo-Alvarado et al. 2015; Pasandideha et al. 2015; Godichaud and Amodeo 2015; Gholamian et al. 2015). Besides, the solution of multi-objective problems is both attractive and challenging (Kao et al. 2014; Jadidia et al. 2015; Ghodratnama et al. 2015; Validi et al. 2014).

As customer interests are rapidly changing, strategies to collaborate with or compete with suitable firms within a network should be considered in the new product development (NPD) process. While in both fields, NPD and supply chain management, have received a considerable attention, they are hardly considered together. Since this paper deals with both the multi-objective optimization and integration of NPD and SC, a brief introduction to the concepts of multi-objective problems in supply chain and integration of NPD and SC is presented below.

In the next two subsections of this paper, the existing literature on multi-objective optimization problems and integration of NPD and SC is reviewed. “Mathematical model and problem descriptions” presents the mathematical model and model’s assumptions. The solving methodology is defined in “Solving methodology”. “Applications and comparisons” presents the computational results and, finally, conclusions are reported in “Conclusions”.

Multi-objective optimization problem in SC

Real SCs are to be optimized simultaneously considering more than one objective. Problems which try to optimize many conflicting objectives simultaneously are called multi-objective optimization problems and have many optimal solutions. The general form of such problem is (Van Veldhuizen 1999):

$$\begin{array}{*{20}c} {\hbox{min} \,F\left( x \right) = \left( {f_{ 1} \left( x \right),f_{ 2} \left( x \right), \ldots ,f_{m} \left( x \right)} \right)} \\ {{\text{s}} . {\text{t}} .\,\left\{ \begin{aligned} g_{i} \left( x \right) \le 0\;\;\quad \quad \,i = 1, \ldots ,q \hfill \\ h_{j} \left( x \right) = 0\;\quad \,\quad j = 1, \ldots ,p, \hfill \\ \end{aligned} \right.} \end{array}$$

where x = (x 1, x 2,…, x n ) ∊ X ⊂ R n is called decision variable and X is n—dimensional decision space. f m (x) is the m-th objective, g i (x) is the i-th constraint inequality and h j (x) is the j-th constraint equation.

Different methodologies found in literature for treating multi-objective optimization problems are the weighted-sum method, the ɛ-constraint method, goal programming method, lexicography methods, LP-metric, maxi-min, fuzzy method, etc. (Chen et al. 2003; Chen and Lee 2004; Guilléna et al. 2004; Hung 2011). In all these mentioned methods, multiple objectives are combined and form a single objective problem and then the optimal solution is obtained. As in real world situations different alternatives are willing by the decision makers, such solutions may not satisfy the decision maker.

For this reason, due to the exponential growth of the problem size and complexity, numerous nature-based multi-objective algorithms are introduced for solving mathematical optimization models. Among various multi-objective optimization algorithms, multi-objective evolutionary algorithms (MOEAs), the most significant ones are multi-objective genetic algorithms (GA) (Deb et al. 2002, Mohapatra et al. 2015), multi-objective particle swarm optimization algorithms (MPSO) (Kotinis 2014; Zhang et al. 2013; Niknam et al. 2011; Tsaia et al. 2010), multi-objective evolutionary algorithms (Shin et al. 2011; Zhu et al. 2014; Tana et al. 2014), multi objective immune clone algorithms (Shang et al. 2012), group search optimizer (Wang et al. 2012), multi-objective frog leaping algorithms (Taher et al. 2010; Safaei Arshia et al. 2014) and so on. However, hybrid algorithms have received considerable attention recently. For instance, Govindan et al. (2015) combined multi-objective electromagnetism mechanism algorithm and adapted multi-objective variable neighborhood search; Bandyopadhyay and Bhattacharya (2013) proposed a modified NSGA-II; Diabat (2014) also combined genetic algorithm with simulated annealing algorithm.

In general, supply chain models naturally lead to complex, large-scale mathematical models which are hard to solve optimally in most real cases. Also, as real SC problems consider more than one objective, the appearance of conflict objectives does not allow simultaneous optimal solutions for all objectives. Thus, for achieving near optimal solutions in large size instances, applying MOEAs are helpful.

Sadeghi et al. (2014) presented a multi-objective combinatorial optimization model of a supply chain problem including one-vendor multi-retailers considering a vendor-managed inventory approach. Their proposed model included two objectives, minimization of inventory cost as the first objective and maximization of the system reliability of the machines that produce the goods as the second. Since the developed model was NP-hard, they applied two multi-objective genetic algorithms, namely, NSGA-II and NRGA, to find Pareto fronts. Latha Shankar et al. (2013) formulated a three-echelon SC network model for the optimal facility location and capacity allocation decisions. While making strategic decisions, they considered fixed location and variable material cost, production, inventory and transportation costs. Their proposed model contained two objective functions, minimizing total SC cost and maximizing fill rate. They applied an intelligent multi-objective hybrid particle swarm optimization algorithm optimizer. As another study, Bandyopadhyay and Bhattacharya (2014) proposed a tri-objective problem for a two-echelon serial supply chain. The considered objectives were the minimization of the total cost the chain, minimization of the variance of order quantity and minimization of the total inventory. To solve the model, they applied a proposed modified NSGA-II. Soleimani and Kannan (2015) developed a deterministic multi-echelon, multi-product, multi-period model for a closed-loop SC network and presented a new hybrid particle swarm optimization and genetic algorithm to solve various kinds of problems. Then a complete computational analysis was under taken to validate their proposed algorithm.

In this paper, a new application of meta-heuristic based on NSGA-II is demonstrated for the proposed tri-objective optimization of SC network considering NPD. The algorithm provides a set of compromised solutions called Pareto optimal solutions which optimize all the conflicting objectives. Then, the solutions satisfying specific criteria can be chosen from the set of Pareto optimal solutions by the decision maker.

Integration of NPD and SC

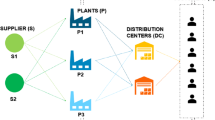
A supply chain network refers to a network which consists of suppliers, manufactures, distributes and customer groups to create products (see Fig. 1). Nowadays, as customer’s preferences change rapidly, to survive in a highly competitive industry, NPD process received more attention. To overcome these challenges, integration of the NPD process and the SC can offer a sustainable competitive advantage to achieve success according to the current competitive environment in the market place. While NPD and SC have drawn considerable attention from the researchers, separately, there is little effort in the literature for covering SC and NPD together.

Fig. 1
figure 1

The stages of a four-echelon SC

Full size image

A generously persuasive parameter for NPD problems in a SC is the strategy of introduction a new product and phasing out the old products which are developed in the planning horizon. As new products appear in the market, the old products could become obsolete, and then phased out. Before launching a new product, a manufacturer must decide the timing of the product launch and the production/sales plan over the planning horizon. According to Billington et al. (1998) there are two rollover strategies namely single product roll and dual product roll to introduce new products to the market. In the first strategy, single product roll, the time phasing out the old product and the time introducing the new product are the same which means that as the new product is introduced the old product is phased out. As such, in dual rollover strategy as the new product is introduced the firm continues producing the old product, in other words, the coexistence of both products is allowed during a certain period of time. In the proposed model the single product rollover is assumed.

SCs through which new products are manufactured need flexibility and responsiveness elements. Each element of a SC echelons may have options which are able to satisfy a required function as the procurement, transportation and production of a product. These decisions after a new product design are completed get more importance because it increases the costs (Simchi-Levi et al. 2000). Naraharisetti and Karimi (2010) proposed the SC redesign and new process introduction in multi-purpose plants. They added some production and inventory facilities, distribution and customer centers to their chain. An integrated optimization model for configuring the SC of new product is developed by Amini and Li (2011). Their work was a first attempt to model the interaction between new product diffusion and SC configuration. The aim of their research is the configuration of SC subject to demand dynamics and other SC parameters such as lead-time and inventory. Also, Li and Amini (2012) developed an integrated optimization model which allowed multiple-sourcing and safety stock placement decisions in coordinate with the demand dynamics during the new product diffusion process throughout its life cycle. As another study, Nepal et al. (2011) have extended a multi-objective optimization model for SC configuration during product development. Their presented model consists of two objectives: maximization of the total compatibility index in strategic alliance and minimization of the total SC costs. Their model improves SC efficiency and stability by jointly considering sourcing, inventory costs and compatibility decisions during the configuration of the SC. They solved their model by using genetic algorithm. As another study, Nager et al. (2014) developed a multi-objective two-stage stochastic programming supply chain model that incorporated imprecise production rate and supplier capacity under scenario dependent fuzzy random demand associated with new product supply chains. The objectives which they considered were maximizing the supply chain profit, achieving desired service level and minimizing the financial risk. They used the possibility measure to quantify the demand uncertainties and solved the model using fuzzy linear programming approach. Jafarian and Bashiri (2014) provided a five echelon dynamic SC model. Their proposed model considers the time of new product lunching in the SC, which is optimized with SC configuration simultaneously. In addition, production, sales, transportation planning and their lead times are considered in the model. In their proposed model each firm individually decides to introduce new products and their model considers developing a single product. Alizadeh Afrouzy et al. (2016) developed a multi-echelon multi-product multi-period optimization model for SC configuration and NPD. Their proposed model incorporates three kinds of products: products which are produced during the planning horizon, products which are decided to be developed and products that are newly introduced during the planning horizon. Their indicated model was capable to determine the optimized lunching time and phasing time during a planning horizontal time in order to maximum the total profit. They applied priority based GA to solve the proposed model. Given the limited number of studies related to the optimization of SCs considering NPD, and in realm contexts in particular, this study tries to contribute to the literature by proposing a multi-objective multi-period model to optimize the profit of SCs considering NPD in accordance to the other two objectives, maximizing the customer satisfaction and maximizing the NPD production. Unlike previous researches, the model considers three categorizes of products; current products, developed products and completely new products. The obtained model belongs to NP-Hard class of the optimization problems, thus, NSGA-II is developed to find a near-optimum solution.

Mathematical model and problem descriptions

Model assumptions

In this paper, a tri-objective, multi-period, multi-product and multi-echelon network including customer groups, distribution centers, manufacturing centers and suppliers is inquired. In this chain, raw materials are supplied from suppliers to manufactures to be transformed into final products and the products are shipped to distribution centers and then according to demands of customer groups they are responded. NPD is assumed to respond to marketplace changes and customers’ tastes to gain or maintain competitive advantage. Accordingly, the company must have the ability to develop and produce new products during the planning horizon and then flexibility is needed for the chain parts to respond to marketplace changes to gain or maintain competitive advantage. As the model is considered multi-product, the categorization of the products is old products, developing/changing products and completely new products. The rollover which is considered in the proposed model is a single-product roll for developing products. This rollover strategy considers the phasing out time, thereby only one of the old or developed products is produced in a moment.

Model formulation

Definitions of variables and parameters in the multi-echelon supply chain network are summarized below. Then, a brief description about the objective functions and constraints of the model are presented.

Indexing sets

t

Index of period,

T

Number of periods

s

Index of supplier,

S

Number of suppliers

f

Index of manufacturer,

F

Number of manufacturers

d

Index of distributor,

D

Number of distributor centers

g

Index of customer group,

G

Number of customer groups

r

Index of raw material,

R

Number of raw materials

i

Index of products

I

Number of products

As discussed in the previous subsection, the products which the company wants to produce during the planning horizon contain three groups. As shown by the indices below, the first group indicates the products that are being produced by the company, the second group relates to the products which are the developed form of the old products and is decided to be produced and the third group contains the completely new products that the company decides to produce during the planning horizon. The indices are as the following:

$$i = \left\{ \begin{array}{ll} o\,({\text{old}})\quad \quad \quad \quad \quad \quad \quad \quad o = 1, \ldots ,O \hfill \\ j\,({\text{old}} \to {\text{new}})\quad \quad \quad \quad \,\,\,\,\,j = O + 1, \ldots ,J \hfill \\ n\,({\text{new}})\quad \quad \quad \quad \quad \quad \quad \,\,\,\,n = J + 1, \ldots ,I \hfill \\ \end{array} \right.$$

Parameters

P oj

1, if product o can be developed to product j, 0, otherwise

D git

Demand of customer group g for product i in period t

PR srt

Per unit price of raw material r in the supplier s in period t

PD i

Per unit price of product i

B ir

Number of the raw material r needed to produce product i

dl i

New product designing duration of product i

CM ft

Capacity of manufacturer f in period t

CD d

Capacity of distributor d

CS srt

Capacity of supplier s for providing raw material r in period t

CP fi

Cost of producing product i in manufacturer f

fCP fi

Fixed cost of producing product i in manufacturer f

TP fi

Hour needed to produce per unit of product i in manufacturer f

TCS sf

Transportation cost between supplier s and manufacturer f

TCM fd

Transportation cost between manufacturer f and distributor center d

TCD dg

Transportation cost between distributor center d and customer group g

CDN i

Cost of designing new product i

M

Big number

Decision variables

SRM sfrt

Amount of raw material r transferred from supplier s to manufacturer f in period t

SMD fdit

Amount of product i transferred from manufacturer f to distributor d in period t

SDG dgit

Amount of product i transferred from distributor d to customer group g in period t

Q fit

Production quantity of product i for manufacturer f in period t

ET it

Binary variable which represents the new product entering time to distributor centers

DP it

1, if company decide to design product i in period t, 0, otherwise

Objective functions

The objectives of the problem are formulated as the following:

$$\begin{aligned} {\text{Maximize }}Z_{1} = \sum\limits_{d} {\sum\limits_{g} {\sum\limits_{i} {\sum\limits_{t} {{\text{PD}}_{i} \,{\text{SDG}}_{dgit} } } } } - \sum\limits_{s} {\sum\limits_{f} {\sum\limits_{r} {\sum\limits_{t} {{\text{PR}}_{srt} \,{\text{SRM}}_{sfrt} } } } } - \sum\limits_{f} {\sum\limits_{i} {\sum\limits_{t} {\left( {{\text{CP}}_{fi} \,Q_{fit} + {\text{fCP}}_{fi} \,{\text{DP}}_{it} } \right)} } } \hfill \\ \quad \, - \sum\limits_{t} {\sum\limits_{s} {\sum\limits_{f} {\sum\limits_{r} {{\text{SRM}}_{sfrt} \,{\text{TCS}}_{sr} } } } } - \sum\limits_{t} {\sum\limits_{d} {\sum\limits_{g} {\sum\limits_{i} {{\text{SDG}}_{dgit} \,{\text{TCD}}_{dg} } } } } - \sum\limits_{t} {\sum\limits_{f} {\sum\limits_{d} {\sum\limits_{i} {{\text{SMD}}_{fdit} \,{\text{TCM}}_{fd} } } } } \hfill \\ \quad - \sum\limits_{t} {\sum\limits_{i} {{\text{CDN}}_{i\,} {\text{DP}}_{it} } } \hfill \\ \end{aligned}$$
(1)
$${\text{Maximize}}\,Z_{ 2} = \sum\limits_{t} {\sum\limits_{i} {\mathop {\hbox{min} }\limits_{g} \left\{ {\frac{{\sum\limits_{d} {{\text{SDG}}_{dgit} } }}{{D_{git} }}} \right\}} }$$
(2)
$${\text{Maximize}}\,\,Z_{ 3} = \sum\limits_{i \in j,n} {\sum\limits_{t} {\sum\limits_{f} {Q_{fit} } } }$$
(3)

The aim of the first objective function which consists of seven cost ingredients is to maximize the total profit at the end of the planning horizon. The first term computes the total revenue of sales. The second term of the objective function represents the purchased quantity for each raw material cost and the next term is the production cost of each product. The next three terms are the transportation costs. Finally, term seventh formulate the cost of designing new products.

The second objective function maximizes the satisfaction level of customer demands. Its aim is to control the amount of lost sales when the chain has the same profit in order to satisfy more customers.

In addition to profit and customer satisfaction, the third objective aims to maximize the production of developed and new products. Although production of developed and new products may not be profitable but the firms have to introduce them to the market in order to survive in the competitive marketplace.

Constraints

$$\sum\limits_{s} {{\text{SRM}}_{sfrt} } = \sum\limits_{i} {B_{ir} \,Q_{fit} } \quad \quad \forall f,t,r$$
(4)
$$Q_{fit} = \sum\limits_{d} {{\text{SMD}}_{fdit} } \quad \quad \forall f,i,t$$
(5)
$$\sum\limits_{f} {{\text{SMD}}_{fdit} } = \sum\limits_{g} {{\text{SDG}}_{dgit} } \quad \forall d,i,t$$
(6)
$$\sum\limits_{d} {{\text{SDG}}_{dgit} \le D_{git} } \quad {\kern 1pt} \,\forall g,i,t$$
(7)
$$\sum\limits_{f} {{\text{SRM}}_{sfrt} } \le {\text{CS}}_{srt} \quad \quad \forall s,r,t$$
(8)
$$Q_{fit} {\text{TP}}_{fi} \le {\text{CM}}_{ft} \quad \quad \forall f,i,t$$
(9)
$$\sum\limits_{f} {\sum\limits_{i} {{\text{SMD}}_{fdit} } } \le {\text{CD}}_{d} \quad \;\forall d,t$$
(10)
$$Q_{fit} \le M \times {\text{ET}}_{it} \quad \quad \forall f,t,i$$
(11)
$$\sum\limits_{{h = t + {\text{dl}}_{i} + 1}}^{T} {{\text{ET}}_{oh} } < {\text{DP}}_{jt} P_{oj} \quad \quad \forall t,i \in o,j$$
(12)
$$\sum\limits_{h = 1}^{{t + {\text{dl}}_{i} }} {{\text{ET}}_{ih} } < {\text{DP}}_{it} \quad \quad \forall t,i \in j,n$$
(13)
$$\sum\limits_{t} {{\text{DP}}_{it} } = 1\quad \quad \forall \,i \in j,n$$
(14)
$${\text{SRM}},\,\,{\text{SMD}},\,\,{\text{SDG}},\,\,Q \ge 0\,\,{\text{and integer}}\,\,{\text{DP}},{\text{ET}} \in \left\{ {0,1} \right\}\quad \quad \forall \,i,t,f,d,s,g,r$$
(15)

The Constraints are presented from Eqs. (4)–(15) and are described briefly in the following. Constrains (4)–(6) describe the amount of flow between the echelons of the chain. Constraint (7) represents that the sales of each product at each customer group during each time period should not exceed its corresponding demand. Inequality (8) ensures that the total raw materials transported from each available supplier to the manufacturers cannot exceed the supplier capacity. Inequalities (9) and (10) also state the same issue about the maximum capacity of available plants and distributors, respectively. Inequality (11) describes the production allowance. Inequality (12) is related to the second category of the products, developing products, which describes the rollover strategy. It states that after deciding to develop or change a product, the manufacturers are able to lunch them after the designing duration time. Inequality (13) describes the start of the designing time. Constraint (14) assures that during the planning horizon each developing or new products are decided to be designed once in the planning horizon. Constraint (15) is the logical binary and non-negativity integer requirements on the decision variables.

Solving methodology

Most real-world optimization problems belong to the class of NP-hard problems. In order to solve NP-hard problems, there are not provably efficient algorithms. Frequently, exact methods cannot solve this class of problems in normal and reasonable time. To optimize this class of problems meta- heuristic algorithms are suitable tools.

For experimentation, this section presents the application of the proposed model along with the proposed NSGA-II algorithm on some random test problems. Some sets of small, medium and large sized instances are considered to evaluate the performance of the solution approach. In addition, since no benchmark is available in the literature to verify and validate the results obtained by NSGA-II, another popular MOEA called NRGA is suggested to solve the problem as well. To do this, some preliminary concepts and principles of NSGA-II and NRGA are first reviewed. Then, the required structures, i.e. chromosome encoding and decoding, crossover and mutation operators are described and the NSGA-II and NRGA are developed.

Introduction to non-dominated sorting genetic algorithm optimization

One of the first evolutionary algorithms which employed the concept of Pareto optimality in solving multi-objective problems is Non-dominated Sorting Genetic Algorithm (Srinivas and Deb 1995). Then Deb et al. (2002) developed a powerful meta-heuristic technique known as NSGA-II which in comparison with NSGA has less computational complexity, less parameters, elitist strategy and is an efficient constraint-handling method. These features have made the NSGA–II very successful and popular in a wide range of engineering problems and some practical works in this area.

As earlier discussed, to improve NPD activities in a SC network the proposed multi-objective model has to be solved. Thus, a multi-objective genetic algorithm on the basis of the NSGA-II is utilized to provide Pareto fronts of the conflicting objectives. Since no benchmarks could be found, the purpose of employing the second algorithm (NRGA) is to verify the results obtained by NSGA-II.

It is noticed that since most real world cases are large scale and NP- hard, it justifies the use of meta-heuristics; however they don’t guarantee to achieve optimal solutions and usually obtain near optima solutions (Talbi 2009; Coello et al. 2002).

The main structure of the NSGA-II which has been so far applied to many complex multi-objective optimization problems successfully is presented as follows.

In an evolution cycle of the standard NSGA-II, the optimization begins by an initial population that is randomly generated and then evaluated by all objective functions. The size of the population is one of the NSGA-II parameters and is often known as pop size. For each and every problem, the population size will depend on the complexity of the problem. Practically, a population size of around 100 individuals is quite frequent, but anyway this size can be changed according to the time and the available memory on the machine compared to the quality of the result to be obtained.

Considering the obtained chromosomes, the population is sorted based on the non-domination principle. Based on the tournament selection the offspring population is created and then the crossover and mutation operators are applied to the obtained chromosomes. Next, the population is sorted based on two criterions: (i) rank and (ii) crowding distance. First, each chromosome is assigned a rank number equal to its non-domination level and then the crowding distance operator is applied between two solutions with equal non-domination rank. Consequently, the required population is organized from the top elements of the front without losing good solutions (elitism). Solutions belonging to the best non-dominated fronts are directly transferred to the mating pool to create the next generation. These steps are repeated until a stopping condition is met. Regarding the termination criteria and iterating the stages mentioned above, the algorithm hopefully presents the best and approximate Pareto optimal solutions.

Important parameters, such as chromosome coding, chromosome decoding and NSGA-II operators are described in more details as follows.

Chromosomes

As same as GA, NSGA-II starts with an initial set of random solutions generally called population. Each individual in the population is called a chromosome. Each chromosome consists of genes and as it is known, a gene in a chromosome is characterized by two factors: locus, the position of the gene within the structure of chromosome and allele, the value the gene takes. In priority-based encoding, the position of a gene is used to represent a node (source/depot in transportation network), and the value is used to represent the priority of the corresponding node for constructing a tree among candidates (Gen and Cheng 2000).

The proposed SC problem involves four-echelons (suppliers, manufacturers, distributor centers, and customer groups). Each chromosome consists of three segments, in which the segments are used to demonstrate the relationship among the four echelons. The first part (Segment 1, Fig. 2) with a dimension of [(S + F) × R] represents the relationship between suppliers and manufacturers in each period which are given as integer numbers belong to 1 to [(S + F) × R] as a priority value. Production of the products in different periods and distribution quantities of the products from manufacturers to distributor centers are considered in the second part (Segment 2, Fig. 2) with a dimension of [(D + F) × I]. Finally, quantities of the distributed products from distributor centers to customer groups in each period are decisions that should be determined in the third part (Segment 3, Fig. 2) with a dimension of [(D + G) × I]. As decisions are made for I products and R raw materials in T periods for S suppliers, F manufactures, D distributor centers, and G customer groups, the full length of a chromosome is the sum of the lengths of these three parts multiplied by the numbers of periods [((D + G) × I) + ((D + F) × I) + ((S + F) × R)] × T. As an example, the structure of a chromosome for one period with two raw materials, five suppliers, two manufacturers, four distributers, two customer groups, three products is shown in Fig. (2).

Fig. 2
figure 2

An example of representation for multi-product multi-echelon SC for one period

Full size image

Since the proposed model improves NPD, as the company decides to produce new products and also develop current products in some periods, this has to be shown in the chromosome. This is done by randomly generating a period and depending on the new product designing duration of each product parameter, the following conversion statements are going to be done:

  1. 1.

    For products which are decided to be produced completely new and for the first time during the planning horizon, depending on the period obtained by randomly generated period plus the designing duration parameter, the genes value for this product is updated in a way that the priority of the related product for the periods up to the determined period is considered zero and the rest remain unchanged.

  2. 2.

    For products which are decided to be developed to another product, depending on the period obtained by sum of randomly generated period and the designing duration parameter, the value of the genes for these products are updated in a way that the priority of the old product from the determined period up to the end of the planning horizon is considered zero and on contrary, the priority of the developed product for the periods up to the determined period is considered zero and the rest remain unchanged.

A chromosome generated by the above procedure is feasible, and the population will not lose diversity.

Decoding procedure for the SC problem

Transportation tree between customer groups and distributor centers, distribution centers and manufacturers, manufacturers and suppliers which are obtained with decoding of the third, second and first segment of a chromosome, respectively, is generated by sequential arc appending between sources and depots. At each step of the decoding procedure, the highest priority in the chromosome is determined. Although its position gives the product type, it gives a source (depot) to realize a shipment for the product type, too. Depending on the selected source (depot), a depot (source) is determined considering minimum transportation cost and an arc between them is added to the corresponding tree (Altiparmak et al. 2009).

The chromosome of SC is decoded on the backward direction. More specifically, the following strategy is taken:

  • First, a transportation tree between customer groups and distribution centers is obtained.

  • In the second step, by the outputs of the third segment and the periods obtained for introducing new and developed products from the third segment, the transportation tree between distribution centers and manufacturers is derived for the second segment.

  • Lastly, the transportation tree between manufacturers and suppliers is obtained for the first segment by the outputs of the second segment. The difference of decoding the first segment from the previous segments is that the obtained periods do not affect this segment and it remains unchanged and the general decoding procedure is applied.

Crossover and mutation operators

In an NSGA-II, similar to GA, the offspring population is determined by a set of operators that recombine and mutate selected members of the current population.

To perform the crossover, two parents are selected based on tournament selection. Then, their periods for developing and introducing new products are exchanged. In other words, when two parents are selected by tournament selection, their priority based chromosomes are updated by the exchanged periods and then is decoded and the fitness function is obtained.

The swap mutation is considered as the mutation operator. The procedure of mutation is summarized as follows: Firstly, a chromosome is randomly extracted. Then, the swap mutation is done. Since the second segments priority based chromosome is related to the third segment, mutation is done only on the third and first segment which are independent. A period is randomly selected for each segment. The operator selects two gens from the corresponding segments and exchanges their places. Since the proposed chromosome considers NPD, note that for the third segment the gens with nonzero value must be swapped.

Introduction to non-dominated ranking genetic algorithm optimization

According to Al Jadaan et al. (2008) in NRGA, roulette wheel selection strategy is considered instead of tournament selection in NSGA-II. In the selection strategy of NRGA, they considered two ranked- based roulette wheel tires; the first tier is for selecting the front, and the second tier is for selecting solution from the front. The individuals in a front are ranked based on their crowding distance, and the fronts ranked based on the non-dominated rank. Initially, a random parent population is created. The procedure is different after the initial generation. Now, two tiers ranked based roulette wheel selection is applied and the solutions belonging to the best non-dominated set to the less probability are chosen. Then the same crossover and mutation operators considered in NSGA-II are used. In addition, to stop the NRGA algorithm, a similar procedure is considered as the one for NSGA-II.

Applications and comparisons

In this section, the application of the two MOGA’s, NSGA-II and NRGA, is presented on some random test problems. Then, they are compared based on some comparison metrics and statistical approaches. To do so, the parameters of the algorithms are tuned via Taguchi method. It should be mentioned that, both algorithms are coded by Matlab 8.2.0.701 (R2013b) software to complete the process of comparison. All computations are run on an Intel(R) Core(TM) i7-4501U CPU@ 2.60 GHz processor laptop.

Multi-objective performance measures

In order to evaluate the performance of multi-objective algorithms, the algorithms are assessed according to multi-objective measures. The metrics which are used to evaluate the performance of the two meta-heuristic algorithms proposed are as follows:

  1. 1.

    Number of Pareto solutions (NPS) which counts the Pareto solutions in the Pareto optimal front.

  2. 2.

    Mean Ideal Distance (MID) which measures the convergence of the Pareto fronts is provided in expression (16) bellow (Deb 2001):

$${\text{MID}} = \frac{{\sum\nolimits_{i = 1}^{N} {d_{i} } }}{N},$$
(16)

where N is number of the solutions in the Pareto optimal front and d i is the Euclidian distance between solution i and the origin and is given as the expression below.

$$d_{i} = \sqrt {f_{1i}^{2} + f_{2i}^{2} + \ldots + f_{ki}^{2} } ,$$
(17)

where f ki is the value of the k-th objective function of the i-th solution.

  1. 3.

    The Divergence Metric (DM) which is provided in expression (18) measures the extension of the Pareto front (Deb 2001).

$${\text{DM}} = \frac{{\sqrt {\sum\limits_{i = 1}^{N} {\left( {\overline{d} - d_{i} } \right)^{2} } } }}{N},$$
(18)

where d i is the Euclidian distance between solution i and solutions j and is given by expression (19) and \(\overline{d}\) is the mean value of the evaluated d i .

$$d_{i} = \mathop {\hbox{min} }\limits_{j = 1, 2, \ldots ,N} \sum\limits_{k = 1}^{M} {(f_{ki} - f_{kj} )} \quad \quad \quad \forall i = 1 ,\ldots ,N,$$
(19)

where f ki and f kj are values of the k-th objective function of the i-th and j-th solutions.

  1. 4.

    The CPU time of running the algorithms to reach near optimum solutions.

Setting model parameters

By considering three problem sizes as small, medium and large, the model’s parameters are set. 12 test problems are considered and generated randomly. They are categorized based on different numbers of supply chain elements. The considered tests and their characteristics are presented in Table 1. Moreover, the following information is also given (Alizadeh Afrouzy et al. 2016).

Table 1 Categorization of small-, medium- and large-sized random test problem
Full size table

  • The demand rate of the customer group g for each product in a period follows a uniform distribution, i.e., D git ∼Uniform [180, 500].

  • The designing cost of new products and the price of each final product have uniform distribution as CDN i ∼Uniform [170, 300] and PD i ∼Uniform [650, 850].

  • Procurement cost of raw material r in suppliers in a period follows a uniform distribution, i.e., PR srt ∼Uniform [5, 18].

  • Transportation cost from supplier s to manufacturers follows a uniform distribution, i.e., TCS sf ∼Uniform [0.12, 0.19].

  • Transportation cost from manufacturer f to distribution centers follows a uniform distribution, i.e., TCM fd ∼Uniform [0.1, 0.7].

  • Transportation cost from distribution center d to customer groups follows a uniform distribution, i.e., TCD dg ∼Uniform [1.2, 1.9].

  • Production fixed cost and cost of producing products in manufactures have uniform distributions as fCP fi ∼Uniform [2, 8] and CP fi ∼Uniform [16, 27].

  • The designing duration time for developing a product and producing a new product is assumed 4 and 2 periods, respectively.

  • For simplicity, in all 12 test problems one product is going to be developed and one product is going to be produced for the first time.

  • The number of raw materials needed to consume a product follows a uniform distribution as B ir  ∼ Uniform [0, 4].

  • Capacities of the manufacturers and distributor centers, and supply capacity of raw material r in a period follow uniform distributions as CM ft ∼Uniform [800, 1500], CD d ∼Uniform [1200, 1900] and CS srt ∼Uniform [3100, 3200], respectively.

  • The hours needed for producing per unit of product i in manufacturers follow a uniform distribution, i.e., TP fi ∼Uniform [3, 6].

Tuning algorithms’ parameters

There are several ways to tune the parameters of the evolutionary algorithms. As choosing suggested amounts by other researches or a trial and error procedure are different ways for tuning the algorithm’s parameters, but methods maybe used to certify qualifications of the solutions which is based on some comparison metrics and statistical approaches. Here the Taguchi method is implemented. Taguchi (1986) developed a family of Fractional Factorial Experiment (FFE) matrices that eventually reduces the total number of the experiments for tuning considerably, but still provides sufficient information. In order to utilize the Taguchi method, the levels of the factors of the considered algorithms are first determined. The aim is to find the amounts of the algorithm’s parameters as input variables to gain an optimal result. Thus, the factors which have an effect on the result are considered as: number of iterations (MaxIt); number of population (N pop); crossover rate (P c) and mutation rate (P m). The levels of the factors are presented in Table 2.

Table 2 Algorithms’ parameters along with their levels
Full size table

According to Table 2, it can be seen that three levels are considered for each factor involved in the algorithms. By the use of Minitab Software, the L9 design which is shown in Table 3 is used for both NSGA-II and NRGA algorithms. Since, 12 test problems are conducted and L9 design is used, 216 problems have been solved and a large amount of data is obtained as results.

Table 3 The orthogonal arrays of the L9 design
Full size table

Results and discussion

Based on the introduced measures in “Multi-objective performance measures”, the performance of the proposed algorithms, NSGA-II and NRGA, are evaluated. Thus, four performance measures are used to compare NSGA-II and NRGA. Under different scenarios of the parameter combinations based on L9 design, first, normalization is done based on the best solution of each measure. This procedure is done using expression (20). Where, for obtaining R the results of each measure is considered separately and Best Sol presents the desirable value which for different measures due to its concept it differs. The proper values for the Best Sol of NPS and DM are the higher value of each measure and conversely, for MID the lower value is considered as the Best Sol. Then the value of R is calculated for each run. Then, by expression (21) they are summed together, which w i represents the weight of each measure based on decision maker’s preference and P i presents the normalized values of the measures. Here the weights are considered 1, 2 and 2 for NPS, MID and DM measures, respectively. The solution with the lower combined value, W, of the normalized objective function values is selected for the best solution from the L9 design of each test problem. Table 4 shows the results of these metrics obtained by NSGA-II and NRGA algorithms using the 12 test problems.

Table 4 Algorithms’ comparison results by Taguchi method
Full size table

For both algorithms, the S/N ratio is obtained by Minitab Software and the results of problem tests 3, 8, 10 and 12 are being shown in Fig. (3). As it is shown in Fig. (3), the optimal solution is obtained in different levels of NSGA-II and NRGA algorithm’s parameters. For instance, in test problem 3, first row of Fig. (3), the optimal results of NSGA-II is obtained when the number of iterations (MaxIt), number of population (N pop), crossover rate (P c) and mutation rate (P m) are considered on levels 3, 3, 1 and 3, respectively, while in NRGA the levels are 2, 1, 2 and 3, respectively.

Fig. 3
figure 3

S/N ratios of the algorithms on test problems 3, 8, 10 and 12

Full size image
$$R = \frac{{\left| {Method\;\,Sol - Best\;\,Sol} \right| \times 1 0 0}}{{\left| {Best\,\;Sol} \right|}}$$
(20)
$$W = \sum\limits_{i = 1}^{I} {w_{i} P_{i} }$$
(21)

As presented in Table 5, since the average of the obtained combined value of three performance measures, W, for NSGA-II is less than NRGA, NSGA-II is more preferable than NRGA. Besides, the CPU time of running the algorithms can be important for decision makers.

Table 5 Algorithms’ comparison results
Full size table

In order to compare the combined value of three performance measures, W, and the CPU time, a popular multi-criteria decision-making method named TOPSIS (Triantaphyllou (2000)) can be used. The considered method ranks the solutions of the problem, which includes conflicting criteria and is helpful for the decision makers to finally decide and make a decision. Table 6 illustrates the decision matrix related to the test problems. As two algorithms and two performance measures are considered, the decision matrix consists of two alternatives and two criteria.

Table 6 Decision matrix for the test problems
Full size table

For employing the TOPSIS method, the decision maker is able to consider the value of the weights according to the criterion’s importance. Based on the criterion’s importance three modes can occur; (1) W and CPU time have the same importance so their weights are equal, (2) W is more important for the decision maker so its weight is greater than CPU time, (3) CPU time has more importance than W so a greater weight is considered for it.

The decision problems are divided into three categories; operational, tactical and strategical problems. As the optimal solution and CPU time, both are important but in the three categorizes mentioned above their importance are somehow different. The optimal solution is more important than CPU time in tactical and strategical problems so it can get a greater weight. However, as the CPU time is more important in operational problems, the considered weight is greater.

Since Production and Location problems are considered as tactical and strategical problems and the proposed model is a Production and Location problem, the optimal solution has more importance. For this reason, the second mode is applied which the weights of W and CPU are considered 0.7 and 0.3, respectively. As it can be seen in the second row of Table 6, NSGA-II showed better results compared with NRGA. However, the other two modes are considered and the results are obtained. Table 6 illustrates the results of ranking using TOPSIS method for the three modes mentioned above.

Based on the results presented in Table 7, NSGA-II showed better results compared with NRGA.

Table 7 The results of ranking using TOPSIS method
Full size table

For further clarifications of the Pareto based algorithms, NSGA-II and NRGA, the Pareto optimal solutions are shown for examples 3, 8, 10 and 12 of the test problems in Fig. 4.

Fig. 4
figure 4

Pareto fronts of the algorithms on test problems 3, 8, 10 and 12

Full size image

Conclusions

This article designs a multi-period multi-echelon multi-product supply chain model. As the aim of the article is considering the profit of the chain due to new product development, the proposed model consists of three objectives which are the maximization of total profit, maximization of the satisfaction level of customer demands and maximization of new product production. Besides the model objectives, the goal is to determine the best and efficient time for introducing new products or changing and developing the current products.

In order to tackle the complex model, the model is solved using two Pareto-based multi-objective evolutionary algorithms known as NSGA-II and NRGA. Next, 12 test problems of different sizes are considered and solved by the proposed algorithms. The parameters of the algorithms were tuned using the Taguchi method. After the algorithms were compared in terms of five performance metrics, the TOPSIS method was implemented to compare the algorithms in terms of multi-objectives metrics. Based on the results, NSGA-II as a multi-objective Pareto-based optimization algorithm, showed better results compared with NRGA.