Introduction

The last four decades witness fundamental works and developments on the fractional derivative and fractional differential equations. Oldham and Spanier [1], Miller and Ross [2], Samko et al. [3], Podlubny [4], Kilbas et al. [5] and others [6, 7] are the pioneer in this field; their works form an introduction to the theory of fractional differential equations and provide a systematic understanding of the fractional calculus such as the existence and the uniqueness of solutions. Hernandez et al. [8] published a paper on recent developments in the theory of abstract differential equations with fractional derivative. Finally, interested various applications of fractional calculus in the field of interdisciplinary sciences such as image processing and control theory have been studied by Magin et al. [9] and Mainardi [10].

In the literature, there exist no methods that produce an exact solution for nonlinear fractional differential equations. Only approximate solutions can be derived using linearization or successive or perturbation methods. Such methods are: variational iteration method and multivariate Pade approximations [11], Iterative Laplace transform method [12], Adomian decomposition method [13–17], Homotopy analysis method [18, 19] and Sumudu transform method [20].

The main objective of this paper is to conduct a new novel technique called residual power series method to study the solution of time-fractional Foam drainage model described by

$$\begin{aligned} D_t^{\alpha }u(x,t)&= \frac{1}{2}u(x,t)u_{xx}(x,t)-2 u^2(x,t)u_x(x,t)+u_x^2(x,t), \end{aligned}$$
(1.1)

subject to the initial conditions:

$$\begin{aligned} u(x,0)&= f(x). \end{aligned}$$
(1.2)

It is a simple model of the flow of liquid through channels (Plateau borders) and nodes (intersection of four channels) between the bubbles, driven by gravity and capillarity [21, 22]. Approximate solutions of Eqs. (1.1)–(1.2) have been obtained by different methods; Adomian decomposition method [23], the Homotopy analysis method [24] and the variational iteration method [25]. It should be noted here that none of the previous studies addressed the accuracy of such methods.

The pattern of the current paper is as follows: In Sect. 2, some definitions and theorems regarding Caputo’s derivative and fractional power series are given. In Sect. 3, we derive a residual power series solution to the time-fractional foam drainage equation. Graphical results regarding the foam drainage model are presented in Sect. 4.

Preliminaries

Many definitions and studies of fractional calculus have been proposed in the literature. These definitions include: Grunwald–Letnikov, Riemann–Liouville, Weyl, Riesz and Caputo sense. In the Caputo case, the derivative of a constant is zero and one can define, properly, the initial conditions for the fractional differential equations which can be handled using an analogy with the classical integer case. For these reasons, researchers prefer to use the Caputo fractional derivative [26] which is defined as

Definition 2.1

For \(m\) to be the smallest integer that exceeds \(\alpha \), the Caputo fractional derivatives of order \(\alpha >0\) are defined as

$$\begin{aligned} D^{\alpha }u(x,t)=\frac{\partial ^{\alpha }u(x,t)}{\partial t^{\alpha }}=\left\{ \begin{array}{ll} \frac{1}{\Gamma (m-\alpha )}\int _{0}^t (t-\tau )^{m-\alpha -1}\frac{\partial ^mu(x,\tau )}{\partial \tau ^m}{\mathrm{d}}\tau , \quad m-1 <\alpha <m\\ \\ \frac{\partial ^mu(x,t)}{\partial t^m}, \quad \alpha =m\in N \end{array}\right. \end{aligned}$$

Now, we survey some needed definitions and theorems regarding the fractional power series (RPS) where there is much theory to be found in [27, 28].

Definition 2.2

A power series expansion of the form

$$\begin{aligned} \sum \nolimits _{m=0}^{\infty }c_m (t-t_0)^{m\alpha }=c_0+c_1(t-t_0)^{\alpha }+c_2(t-t_0)^{2\alpha }+\cdots \quad 0\le n-1 <\alpha \le n,\quad t \le t_0 \end{aligned}$$

is called fractional power series PS about \(t=t_0\)

Theorem 2.1

Suppose that \(f\) has a fractional PS representation at \(t=t_0\) of the form

$$\begin{aligned} f(t)=\sum \nolimits _{m=0}^{\infty }c_m (t-t_0)^{m\alpha }, \quad t_0\le t < t_0+R. \end{aligned}$$

If \(D^{m\alpha } f(t),\ \ m=0,1,2,\ldots \) are continuous on \((t_0, t_0+R)\) , then \(c_m=\frac{D^{m\alpha } f(t_0)}{\Gamma (1+m\alpha )}.\)

Definition 2.3

A power series expansion of the form

$$\begin{aligned} \sum \nolimits _{m=0}^{\infty }f_m(x)(t-t_0)^{m\alpha } \end{aligned}$$

is called multiple fractional power series PS about \(t=t_0\)

Theorem 2.2

Suppose that \(u(x,t)\) has a multiple fractional PS representation at \(t=t_0\) of the form

$$\begin{aligned} u(x,t)=\sum \nolimits _{m=0}^{\infty }f_m(x) (t-t_0)^{m\alpha }, \quad x \in I, \quad t_0\le t < t_0+R. \end{aligned}$$

If \(D_t^{m\alpha } u(x,t),\quad m=0,1,2,\ldots \) are continuous on \(I\times (t_0, t_0+R)\) , then \(f_m(x)=\frac{D_t^{m\alpha } u(x,t_0)}{\Gamma (1+ m\alpha )}.\)

From the last theorem, it is clear that if \(n+1\)-dimensional function has a multiple fractional PS representation at \(t=t_0\), then it can be derived in the same manner, i.e.

Corollary 2.3

Suppose that \(u(x,y,t)\) has a multiple fractional PS representation at \(t=t_0\) of the form

$$\begin{aligned} u(x,y,t)=\sum \nolimits _{m=0}^{\infty }g_m(x,y) (t-t_0)^{m\alpha },\ \ \ (x,y) \in I_1\times I_2,\ \ t_0\le t < t_0+R. \end{aligned}$$

If \(D_t^{m\alpha } u(x,y,t),\ \ m=0,1,2,\ldots \) are continuous on \(I_1\times I_2 \times (t_0, t_0+R)\) , then \(g_m(x,y)=\frac{D_t^{m\alpha } u(x,y,t_0)}{\Gamma (1+ m\alpha )}.\)

Next, we present in details the derivation of the residual power series solution to the generalized fractional DSW system.

Residual power series (RPS) of the foam drainage model

The aim of this section is to construct power series solution to the time-fractional Foam drainage model by substituting its power series (PS) expansion among its truncated residual function [29, 30]. From the resulting equation, a recursion formula for the computation of the coefficients is derived, while the coefficients in the fractional PS expansion can be computed recursively by recurrent fractional differentiation of the truncated residual function.

The RPS method proposes the solution for Eqs. (1.1–1.2) as a fractional PS about the initial point \(t=0\)

$$\begin{aligned} u(x,t)&= \sum _{n=0}^{\infty }f_n(x)\frac{t^{n\alpha }}{\Gamma (1+n\alpha )},\quad 0<\alpha \le 1,\ x\in I,\quad 0\le t<R. \end{aligned}$$
(3.1)

Next, we let \(u_k(x,t)\) to denote the k-th truncated series of \(u(x,t)\), i.e.,

$$\begin{aligned} u_k(x,t)&= \sum _{n=0}^{k}f_n(x)\frac{t^{n\alpha }}{\Gamma (1+n\alpha )},\quad 0<\alpha \le 1,\quad x\in I,\ 0\le t<R. \end{aligned}$$
(3.2)

It is clear that by condition (1.2) the \(0\)-th RPS approximate solutions of \(u(x,t)\) is

$$\begin{aligned} u_0(x,t)&= f_0(x)=u(x,0)=f(x). \end{aligned}$$
(3.3)

Also, Eq. (3.2) can be written as

$$\begin{aligned} u_k(x,t)&= f(x)+\sum _{n=1}^{k}f_n(x)\frac{t^{n\alpha }}{\Gamma (1+n\alpha )},\quad 0<\alpha \le 1,\ x\in I, \ 0\le t<R,\ k=1,2,3,\ldots \end{aligned}$$
(3.4)

Now, we define the residual functions, \(Res\), for Eq. (1.1)

$$\begin{aligned} Res_u(x,t)&= D_t^{\alpha }u(x,t)-\frac{1}{2}u(x,t)u_{xx}(x,t)+2 u^2(x,t)u_x(x,t)-u_x^2(x,t), \end{aligned}$$
(3.5)

and, therefore, the \(k\)-th residual function, \(Res_{u,k}\), is

$$\begin{aligned} Res_{u,k}(x,t)&= D_t^{\alpha }u_k(x,t)-\frac{1}{2}u_k(x,t)\frac{\partial ^2}{\partial x^2} u_k(x,t)+2u_k^2(x,t)\frac{\partial }{\partial x} u_k(x,t)-\left( \frac{\partial }{\partial x} u_k(x,t)\right) ^2. \end{aligned}$$
(3.6)

As in [29, 30], \(Res(x,t)=0\) and \(\lim _{k\rightarrow \infty }Res_k(x,t)=Res(x,t)\) for all \(x\in I\) and \(t\ge 0\). Therefore, \(D_t^{r\alpha }Res(x,t)=0\) since the fractional derivative of a constant in the Caputo’s sense is \(0\). Also, the fractional derivative \(D_t^{r\alpha }\) of \(Res(x,t)\) and \(Res_k(x,t)\) is matching at \(t=0\) for each \(r=0,1,2,\ldots ,k\).

To clarify the RPS technique, we substitute the \(k\)-th truncated series of \(u(x,t)\) into Eq. (3.6), find the fractional derivative formula \(D_t^{(k-1)\alpha }\) of both \(Res_{u,k}(x,t),\ \ k=1,2,3,\ldots ,\) and then solve the obtained algebraic system

$$\begin{aligned} D_t^{(k-1)\alpha }Res_{u,k}(x,0)&= 0,\ 0<\alpha \le 1,\ x\in I,\ k=1,2,3\ldots \end{aligned}$$
(3.7)

to get the required coefficients \(f_n(x),\ \ n=1,2,3,\ldots ,k\) in Eq. (3.4). Now, we follow the following steps.

Step 1. To determine \(f_1(x)\), we consider \((k=1)\) in (3.6)

$$\begin{aligned} Res_{u,1}(x,t)&= D_t^{\alpha }u_1(x,t)-\frac{1}{2}u_1(x,t)\frac{\partial ^2}{\partial x^2} u_1(x,t)+2u_1^2(x,t)\frac{\partial }{\partial x} u_1(x,t)-\left( \frac{\partial }{\partial x} u_1(x,t)\right) ^2. \end{aligned}$$
(3.8)

But, \(u_1(x,t)=f(x)+f_1(x) \frac{t^{\alpha }}{\Gamma (1+\alpha )}\). Therefore,

$$\begin{aligned} Res_{u,1}(x,t)&= f_1(x)-\frac{1}{2}\left( f(x)+f_1(x)\frac{t^{\alpha }}{\Gamma (1+\alpha )}\right) \left( f''(x)+f_1''(x)\frac{t^{\alpha }}{\Gamma (1+\alpha )}\right) \nonumber \\&\quad +2\left( f(x)+f_1(x)\frac{t^{\alpha }}{\Gamma (1+\alpha )}\right) ^2\left( f'(x)+f_1'(x)\frac{t^{\alpha }}{\Gamma (1+\alpha )}\right) \nonumber \\&\quad -\left( f'(x)+f_1'(x)\frac{t^{\alpha }}{\Gamma (1+\alpha )}\right) ^2. \end{aligned}$$
(3.9)

From Eq. (3.7), we deduce that \(Res_{u,1}(x,0)=0\) and thus,

$$\begin{aligned} f_1(x)&= \frac{1}{2}f(x)f''(x)-2f^2(x)f'(x)+f'^2(x) \end{aligned}$$
(3.10)

Therefore, the \(1\)st RPS approximate solution is

$$\begin{aligned} u_1(x,t)&= f(x)+\left( \frac{1}{2}f(x)f''(x)-2f^2(x)f'(x)+f'^2(x)\right) \frac{t^{\alpha }}{\Gamma (1+\alpha )}. \end{aligned}$$
(3.11)

Step 2. To obtain \(f_2(x)\), we substitute the \(2\)nd truncated series \(u_2(x,t)=f(x)+f_1(x) \frac{t^{\alpha }}{\Gamma (1+\alpha )}+f_2(x) \frac{t^{2\alpha }}{\Gamma (1+2\alpha )}\) into the \(2\)nd residual function \(Res_{u,2}(x,t)\), i.e.,

$$\begin{aligned} Res_{u,2}(x,t)&= D_t^{\alpha }u_2(x,t)-\frac{1}{2}u_2(x,t)\frac{\partial ^2}{\partial x^2} u_2(x,t)+2u_2^2(x,t)\frac{\partial }{\partial x} u_2(x,t)-\left( \frac{\partial }{\partial x} u_2(x,t)\right) ^2.\nonumber \\&= f_1(x)+f_2(x)\frac{t^{\alpha }}{\Gamma (1+\alpha )}-\frac{1}{2}\left( f(x)+\cdots +f_2(x)\frac{t^{2\alpha }}{\Gamma (1+2\alpha )}\right) \nonumber \\&\quad \times \left( f''(x)+\cdots +f_2''(x)\frac{t^{2\alpha }}{\Gamma (1+2\alpha )}\right) \nonumber \\&\quad +2\left( f(x)+\cdots +f_2(x)\frac{t^{2\alpha }}{\Gamma (1+2\alpha )}\right) ^2\left( f'(x)+\cdots +f_2'(x)\frac{t^{2\alpha }}{\Gamma (1+2\alpha )}\right) \nonumber \\&\quad -\left( f'(x)+\cdots +f_2'(x)\frac{t^{2\alpha }}{\Gamma (1+2\alpha )}\right) ^2. \end{aligned}$$
(3.12)

Applying \(D_t^{\alpha }\) on both sides of Eq. (3.12) gives

$$\begin{aligned} D_t^{\alpha }Res_{u,2}(x,t)&= f_2(x)-\frac{1}{2}\left( f_1(x)+f_2(x)\frac{t^{\alpha }}{\Gamma (1+\alpha )}\right) \times \left( f''(x)+\cdots +f_2''(x)\frac{t^{2\alpha }}{\Gamma (1+2\alpha )}\right) \nonumber \\&\quad -\frac{1}{2}\left( f(x)+\cdots +f_2(x)\frac{t^{2\alpha }}{\Gamma (1+2\alpha )}\right) \times \left( f_1''(x)+f_2''(x)\frac{t^{\alpha }}{\Gamma (1+\alpha )}\right) \nonumber \\&\quad +4\left( f(x)+\cdots +f_2(x)\frac{t^{2\alpha }}{\Gamma (1+2\alpha )}\right) \left( f_1(x)+f_2(x)\frac{t^{\alpha }}{\Gamma (1+\alpha )}\right) \nonumber \\&\quad \times \left( f'(x)+\cdots +f_2'(x)\frac{t^{2\alpha }}{\Gamma (1+2\alpha )}\right) \nonumber \\&\quad +2\left( f(x)+\cdots +f_2(x)\frac{t^{2\alpha }}{\Gamma (1+2\alpha )}\right) ^2 \left( f_1'(x)+f_2'(x)\frac{t^{\alpha }}{\Gamma (1+\alpha )}\right) \nonumber \\&\quad -2\left( f'(x)+\cdots +f_2'(x)\frac{t^{2\alpha }}{\Gamma (1+2\alpha )}\right) \left( f_1'(x)+f_2'(x)\frac{t^{\alpha }}{\Gamma (1+\alpha )}\right) . \end{aligned}$$
(3.13)

By the fact that \(D_t^{\alpha }Res_{u,2}(x,0)=0\) and solving the resulting system in (3.13) for the unknown coefficient function \(f_2(x)\), we get

$$\begin{aligned} f_2(x)&= \frac{1}{2}f(x)f_1''(x)+\frac{1}{2}f_1(x)f''(x)-4f(x)f_1(x)f'(x)-2f^2(x)f_1'(x)+2f'(x)f_1'(x). \end{aligned}$$
(3.14)

Step 3. We derive the formula of the coefficient function \(f_3(x)\). Substitute the \(3\)rd truncated series \(u_3(x,t)=f(x)+f_1(x) \frac{t^{\alpha }}{\Gamma (1+\alpha )}+f_2(x) \frac{t^{2\alpha }}{\Gamma (1+2\alpha )}+f_3(x) \frac{t^{3\alpha }}{\Gamma (1+3\alpha )}\) into the \(3\)rd residual function \(Res_{u,3}(x,t)\). i.e.,

$$\begin{aligned} Res_{u,3}(x,t)&= D_t^{\alpha }u_3(x,t)-\frac{1}{2}u_3(x,t)\frac{\partial ^2}{\partial x^2} u_3(x,t)+2u_3^2(x,t)\frac{\partial }{\partial x} u_3(x,t)-\left( \frac{\partial }{\partial x} u_3(x,t)\right) ^2.\nonumber \\&= f_1(x)+f_2(x)\frac{t^{\alpha }}{\Gamma (1+\alpha )}+f_3(x)\frac{t^{2\alpha }}{\Gamma (1+2\alpha )}- \frac{1}{2}\left( f(x)+\cdots +f_3(x)\frac{t^{3\alpha }}{\Gamma (1+2\alpha )}\right) \nonumber \\&\quad \times \left( f''(x)+\cdots +f_3''(x)\frac{t^{3\alpha }}{\Gamma (1+3\alpha )}\right) \nonumber \\&\quad +2\left( f(x)+\cdots +f_3(x)\frac{t^{3\alpha }}{\Gamma (1+3\alpha )}\right) ^2 \left( f'(x)+\cdots +f_3'(x)\frac{t^{3\alpha }}{\Gamma (1+3\alpha )}\right) \nonumber \\&\quad -\left( f'(x)+\cdots +f_3'(x)\frac{t^{3\alpha }}{\Gamma (1+3\alpha )}\right) ^2\!. \end{aligned}$$
(3.15)

Now, we apply the operator \(D_t^{2\alpha }\) on both sides of Eq. (3.15)

$$\begin{aligned} D_t^{2\alpha }Res_{u,3}(x,t)&= D_t^{\alpha }\left( D_t^{\alpha } Res_{x,3}(x,t)\right) \nonumber \\&= f_3(x)-\left( f_1(x)+\cdots +f_3(x)\frac{t^{2\alpha }}{\Gamma (1+2\alpha )}\right) \left( f_1''(x)+\cdots +f_3''(x)\frac{t^{2\alpha }}{\Gamma (1+2\alpha )}\right) \nonumber \\&\quad -\frac{1}{2}\left( f_2(x)+f_3(x)\frac{t^{\alpha }}{\Gamma (1+\alpha )}\right) \left( f''(x)+\cdots +f_3''(x)\frac{t^{3\alpha }}{\Gamma (1+3\alpha )}\right) \nonumber \\&\quad -\frac{1}{2}\left( f(x)+\cdots +f_3(x)\frac{t^{3\alpha }}{\Gamma (1+3\alpha )}\right) \left( f_2''(x)+f_3''(x)\frac{t^{\alpha }}{\Gamma (1+\alpha )}\right) \nonumber \\&\quad +4\left( f_1(x)+\cdots +f_3(x)\frac{t^{2\alpha }}{\Gamma (1+2\alpha )}\right) ^2 \left( f'(x)+\cdots +f_3'(x)\frac{t^{3\alpha }}{\Gamma (1+3\alpha )}\right) \nonumber \\&\quad +4\left( f(x)+\cdots +f_3(x)\frac{t^{3\alpha }}{\Gamma (1+3\alpha )}\right) \left( f_2(x)+f_3(x)\frac{t^{\alpha }}{\Gamma (1+\alpha )}\right) \nonumber \\&\quad \times \left( f'(x)+\cdots +f_3'(x)\frac{t^{3\alpha }}{\Gamma (1+3\alpha )}\right) \nonumber \\&\quad +8\left( f(x)+\cdots +f_3(x)\frac{t^{3\alpha }}{\Gamma (1+3\alpha )}\right) \left( f_1(x)+\cdots +f_3(x)\frac{t^{2\alpha }}{\Gamma (1+2\alpha )}\right) \nonumber \\&\quad \times \left( f_1'(x)+\cdots +f_3'(x)\frac{t^{2\alpha }}{\Gamma (1+2\alpha )}\right) \nonumber \\&\quad +2\left( f(x)+\cdots +f_3(x)\frac{t^{3\alpha }}{\Gamma (1+3\alpha )}\right) ^2\left( f_2'(x)+f_3'(x)\frac{t^{\alpha }}{\Gamma (1+\alpha )}\right) \nonumber \\&\quad -2\left( f_1'(x)+\cdots +f_3'(x)\frac{t^{2\alpha }}{\Gamma (1+2\alpha )}\right) ^2\nonumber \\&\quad -2\left( f'(x)+\cdots +f_3'(x)\frac{t^{3\alpha }}{\Gamma (1+3\alpha )}\right) \left( f_2'(x)+f_3'(x)\frac{t^{\alpha }}{\Gamma (1+\alpha )}\right) . \end{aligned}$$
(3.16)

Thus, solving the equation \(D_t^{2\alpha }Res_{u,3}(x,0)=0\) results in the following recurrence formula

$$\begin{aligned} f_3(x)&= f_1(x)f_1''(x)+\frac{1}{2}f(x)f_2''(x)+\frac{1}{2}f_2(x)f''(x)-4f_1^2(x)f'(x)-4f(x)f_2(x)f'(x)\nonumber \\&\quad -8f(x)f_1(x)f_1'(x)-2f^2(x)f_2'(x)+2\left( f_1'(x)\right) ^2+2f'(x)f_2'(x). \end{aligned}$$
(3.17)

Finally, we follow the same manner as above and solve the equation \(D_t^{3\alpha }Res_{u,4}(x,0)=0\) to deduce the following result

$$\begin{aligned} f_4(x)&= \frac{3}{2}f_2(x)f_1''(x)+\frac{3}{2}f_1(x)f_2''(x)+\frac{1}{2}f_3(x)f''(x)+\frac{1}{2}f(x)f_3''(x)\nonumber \\&\quad -12 f_1(x)f_2(x)f'(x)-12 f_1^2(x)f_1'(x)-4f(x)f_3(x)f'(x)-8f(x)f_2(x)f_1'(x)\nonumber \\&\quad -8f(x)f_1(x)f_2'(x)-2f^2(x)f_3'(x)+6f_1'(x)f_2'(x)+2f'(x)f_3'(x). \end{aligned}$$
(3.18)

By the above recurrence relations, we are ready to present some graphical results regarding the time-fractional Foam drainage model.

Applications and results

The purpose of this section is to test the derivation of residual power series solutions of the following time-fractional foam drainage equation.

$$\begin{aligned} D_t^{\alpha }u(x,t)&= \frac{1}{2}u(x,t)u_{xx}(x,t)-2 u^2(x,t)u_x(x,t)+u_x^2(x,t), \end{aligned}$$
(4.1)

subject to the initial conditions:

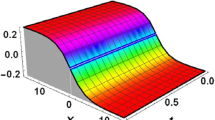
$$\begin{aligned} u(x,0)&= -\sqrt{c}\tanh (\sqrt{c} x). \end{aligned}$$
(4.2)

Where the exact solution of this model when \(\alpha =1\) is \(u(x,t)=-\sqrt{c}\tanh (\sqrt{c} (x-ct))\). Based on the obtained results from the previous section, we consider only the \(4{th}\) RPS approximate solution. Figure 1 represents the \(4\)th RPS approximate solution of the function \(u(x,t)\) for different values of the fractional derivative \(\alpha \). To validate the efficiency and accuracy of the analytical scheme, we give explicit values of \(x\) and \(t\) and compute the absolute error compared with the exact solution when \(\alpha =1\) (See Table 1). Figure 2 represents solutions to the fractional foam drainage when the initial condition is \(f(x)=x\) for \(\alpha =0.5,\ 1\). Finally, Fig. 3 represents solutions to the fractional foam drainage when the initial condition is \(f(x)=\sin (x)\) for \(\alpha =0.5,\ 0.75,\ 1\).

In the theory of fractional calculus, it is obvious that when the fractional derivative \(n-1<\alpha < n\) tends to positive integer \(n\), the approximate solution continuously tends to the exact solution of the problem with derivative \(n=1\). It is also clear from Figs. 1, 2 and 3 that when \(\alpha \) is close to 0, the solutions bifurcate and provide wave-like pattern. But, when \(\alpha \) is close to 1, there is no pattern.

Fig. 1
figure 1

The \(4\)th RPS approximate solution of the Foam model when \(f(x)=-\sqrt{c}\tanh (\sqrt{c} x)\): a \(u_4(x,t,,\alpha =0.7)\), b \(u_4(x,t,\alpha =0.8)\), c \(u_4(x,t,\alpha =0.9)\), d \(u_4(x,t,\alpha =1)\), e \(u(x,t)\) for \(\alpha =1\), \(-5<x<5,\ \ 0<t<0.1\)

Full size image
Table 1 The obtained errors \(|u_{exact}-u^4_{approx}|\) for the RPS method
Full size table
Fig. 2
figure 2

The \(4\)th RPS approximate solution of the Foam model when \(f(x)=x\): a \(u_4(x,t,\alpha =0.5)\), b \(u_4(x,t,\alpha =0.75)\), c \(u_4(x,t,\alpha =1)\), \(-4<x<4,\ \ 0<t<0.1\)

Full size image
Fig. 3
figure 3

The \(4\)th RPS approximate solution of the Foam model when \(f(x)=\sin (x)\): a \(u_4(x,t,\alpha =0.5)\), b \(u_4(x,t,\alpha =0.75)\), c \(u_4(x,t,\alpha =1)\), \(-5<x<5,\ \ 0<t<0.1\)

Full size image

Conclusions

A new analytical iterative technique based on the residual power series is proposed to obtain an approximate solution to a nonlinear time-fractional foam drainage equation. Three different initial conditions of the Foam model are considered and accordingly different physical behaviors are produced. We observed when \(\alpha \) is close to 0, the solutions bifurcate and provide wave-like pattern. But, when \(\alpha \) is close to 1, there is no pattern (Figs. 1 and 3). This bifurcation phenomenon will help the researchers to open many new avenues to better understanding of time-fractional derivatives and its relation to real-life phenomena. The accuracy of the proposed method has been tested by studying the absolute errors of the obtained approximate of the Foam model (Table 1). The RPS method is a promising technique based on its simplicity and accuracy. It is to be considered an additive tool for the field of fractional theory and computations. As future work, we will extend the RPS method to handle (\(2+1\))-dimensional linear and nonlinear space- and time-fractional physical models.