Early Mission Design of Transfers to Halo Orbits via Particle Swarm Optimization

Abstract

Particle Swarm Optimization (PSO) is used to prune the search space of a low-thrust trajectory transfer from a high-altitude, Earth orbit to a Lagrange point orbit in the Earth-Moon system. Unlike a gradient based approach, this evolutionary PSO algorithm is capable of avoiding undesirable local minima. The PSO method is extended to a “local” version and uses a two dimensional search space that is capable of reducing the computation run-time by an order of magnitude when compared with published work. A technique for choosing appropriate PSO parameters is demonstrated and an example of an optimized trajectory is discussed.

Appendix:

This appendix describes the methods used to appropreately choose the various optimization paramaters of the PSO method as applied to the example problem. The same technique can be applied to other problems with little modification.

Sizing N _p

The PSO algorithm was run multiple times with $r_{\text {local}} = \left [\frac {1}{20},\frac {1}{16}\right ]^{T}$ and $j_{\max } = 15$. Each data point in Table 2 was averaged over 10 identical trials with only the difference being the initial χ and ω values which are chosen randomly. Referring to Fig. 7, one will note that the average value of the cost function, J _best decreases as a function of N _p, as expected. Initially, the decrease is substantial but the amount of increase diminishes as each additional particle is added to the system—especially for values of N _p>400. Based on this data it seems reasonable to conclude that the ideal range of N _p lies somewhere between 200 and 400 particles. A PSO algorithm with less particles experiences a huge amount of variability and offers a relatively poor average J _best (i.e. the N _p=50 data point). Conversely, a PSO algorithm utilizing more than 400 particles will consume copious amounts of CPU time without a significant decrease in the average J _best identified.

Fig. 7

Values of J _{b e s t} as a function of N _p for a fixed value of j _{m a x} =15 iterations. Data taken from Table 2

Table 2 Cost, convergence, and CPU time for j _{m a x} =15 iterations and various number of particles (N _p )

Sizing j _{m a x} via the Convergence Metric, γ

In the previous section, a method for determining the appropriate value of N _p was presented. This section develops a new metric that is used to determine an appropriate number of iterations to use when terminating the PSO algorithm. In general, there are two ways to accomplish this task. The first method is to simply select a value for j _{m a x} before running the PSO algorithm. An appropriate value of j _{m a x} is highly problem dependent and relies greatly on the experience and intuition of the researcher [13, 28]. A new metric, γ, is proposed, in this paper, to replace j _{m a x} as the trigger that terminates the PSO algorithm.

The top plot in Fig. 8 displays convergence (γ) as a function of PSO iteration (j) for a system of 50 particles. Each point is averaged over 10 (identical) data trials and is plotted with ±1σ error bars. Note that the convergence seems to initially increase exponentially with low values of j but then logarithmically approaches an asymptote for large values of j. This seems to indicate that, for large numbers of PSO iterations, an increasingly diminishing rate of marginal convergence is achieved. This relationship has been successfully fitted to the following curve using MATLAB’s curve fitting toolbox:

$$ c \exp \left( \frac{-b}{(j + a)^{3}} \right) $$

(A-1)

with the fitted values of the constants being a=7, b=2421, and c=08671 with a “goodness of fit” measured as R ²=09957. In general, γ _{m a x} ≤c≤1 since the value of Eq. A-1 is c when $j = \infty$. Of course theory dictates that γ _{m a x} →1 as $j_{max} \to \infty$. In practice, however, this is not always the case since a small number of particles can become trapped in cycles that oscillate them between the neighborhood of one local minima and another. Also, on occasion, a particle will oscillate for a very long time between a personal best and global best value that are in opposite directions.

Fig. 8

Top: Convergence (γ) as a function of iteration number (j). Bottom: Cost (J) as a function of iteration number (j)

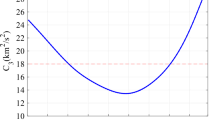
The bottom plot in Fig. 8 displays the cost (J) as a function of PSO iteration (j) for the same system of 50 particles and 10 trials. The plot describes the evolution of the best value of the cost function. Note the exponential decay displayed in the cost function and fitted to the following curve:

$$ ae^{-bj} + c $$

(A-2)

where the values of the fitted constants are a=0174, b=02344, and c=01314 with R ²=09879. As $j \to \infty$ the limit of Eq. A-2

$$ \underset{j \to \infty}{\lim} (ae^{-bj} + c) = c $$

(A-3)

is equal to 01314 which is a greater value than J _{b e s t} =01225. J _{b e s t} is indicated by the dashed line in the bottom plot of Fig. 8, where J _{b e s t} represents the lowest value of the cost function encountered by any particle from any of the 10 trials. The difference between J _{b e s t} and c is reflected in the variability of the last few data points in the plot where J=01327±00092(±1σ) or a range of $J (j = 30)_{range} = [01225 \leftrightarrow 01520]$.

Based on the data found in Fig. 8 it seems reasonable to conclude that a value of γ ≥075 is a suitable choice of terminal convergence to end the PSO algorithm. This roughly correlates to $j = [15 \leftrightarrow 20]$ iterations and places the value of the cost function very near its asymptotic limit without wasting CPU time on additional and unproductive iterations. It therefore seems reasonable to use a value of γ _{s t o p} =08 as a conservative termination metric for the PSO algorithm. Inserting this value into Eq. A-1 and solving for j yields j _{s t o p} =24 iterations on average.

Effect of the Product N _p j _{m a x} on the Optimal Solution

Since the most significant issue with PSO is the CPU run-time, and CPU run-time is proportional to the product N _p j _{m a x} , it is reasonable to investigate the trade between N _p and j _{m a x} while holding the number of integrated trajectories (and CPU run-time) fixed. This data is presented in Fig. 9 which plots J _{b e s t} vs. the log of N _p (semi-log plot was chosen for illustrative purposes) given a fixed value of the product N _p j _{m a x} =3000 evaluations (trajectories integrated according to Eq. 1). Values of j _{m a x} included [4,8,15,30,60]. Note that the lowest value of J _{b e s t} was captured when N _p =200 and j _{m a x} =15. This roughly agrees with the recommended values of N _p and j _{m a x} (or γ _{s t o p} ) developed in the two previous sections of this paper.

Fig. 9

Plot of J _{b e s t} as a function of $\ln (j_{max})$ for a fixed value of 3,000 integrations per point. Each point was averaged over 10 identical trials with ±1σ error bounds drawn

Effect of r _{l o c a l} on the Optimal Solution

The effect of the size of r _{l o c a l} on the convergence and cost is best captured in Fig. 10. These plots are produced by multiplying r _{l o c a l} by a scaling factor. The scaling factors used in this study are $\|r\| = \left [\frac {1}{4}, \frac {1}{2}, 1, 2, 4, 8\right ]$ where r _{r e s i z e d} =∥r∥r _{l o c a l} . Each data point was averaged over 10 identical trials and plotted with ±1σ error bars using 50 particles and 15 iterations. Note that the convergence is not significantly affected by a change in the magnitude of r _{l o c a l} , as is evidenced by the fact that any data point lies within the error bars of any of the remaining points. Likewise, the cost typically is not affected by the magnitude of r _{l o c a l} except for extremely small values of ∥r∥, as evidenced by the left plot in Fig. 10; in which case the size of a particle’s local range of communication is so small it is effectively “blind and deaf.”

Fig. 10

Left: Cost as a function of radius. Right: Convergence as a function of radius

Figure 11 displays a map of local minima identified by the PSO algorithm as plotted in k τ-space. In this particular example ∥r∥=1 and seven local minima are identified. A green ellipse of size $r_{local} = \left [ \frac {1}{20}, \frac {1}{16} N \right ]_{T}$ is drawn around each local minima to illustrate the communication limit between a particle at the local minima and any nearby particle it can communicate with. This plot illustrates the ability of the local PSO algorithm to simultaneously interrogate multiple local minima instead of being limited to only one minimum using the traditional PSO algorithm.

Fig. 11

A map of the final positions of 50 particles after 15 iterations. The ellipses are drawn around local swarms of two or more particles indicating a local minimum. The size of the ellipse reflects the dimensions of $r_{local} = \left [ \frac {1}{20}, \frac {1}{16} N \right ]$