Abstract
The formalization of correctness and optimality concepts, which are desirable requirements for interval (and other self-validated methods) libraries, is related to topological aspects of real numbers and Moore arithmetics, characterizing some families of interval functions. The main motivation is that real continuous functions are largely used in many fields of human activity, and a characterization of their interval representation in terms of interval topologies leads to the knowledge of how interval algorithms are suitable to represent those functions. In this paper, we characterize and relate some classes of interval functions with respect to three natures of an interval (as a set, as an information, as a number). These natures establish different ways to classify intervals, and hence different notions of continuity. Here we relate the notion of interval representations with those classes of functions.


Similar content being viewed by others
Notes
Observe that \(d(a,b)=d(b,a)=0\) and \(a\ne b\) do not hold, but \(d(a,b)=d(b,a)\ne 0\) and \(a=b\), and \(d(a,b)=d(b,a)\ne 0\) and \(a\ne b\) can hold.
Note that when \(q\) is a metric, \(q,\overline{q},\) and \(q^*\) coincide and the topological spaces are the same.
More formally \(F\) is bi-continuous if for every bi-directed set—let \(\mathcal D =(D,\le )\) be a poset. \(\Delta \subseteq D\) is bi-directed if \(\Delta \) is a directed set of \(\mathcal D \) and \(\mathcal D ^\mathrm{op}=(D,\ge )\)—\(F(\bigsqcup \Delta )=\bigsqcup F(\Delta )\) and
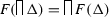 .
.For us, a real function \(f\) is asymptotic if for some interval \([a,b]\), the set \(\{f(x^{\prime }): a\le x^{\prime }\le b\}\) has no supremum or no infimum.
For every interval \(A\), \(F(A)\sqsubseteq G(A)\).
For every interval \(A\), \(F(A)\sqsubseteq \mathrm{CIR}(f)(A)\).
References
Acióly BM (1991) Computational foundations of interval mathematics. PhD thesis, Instituto de Informática, Universidade Federal do Rio Grande do Sul, Dezembro 1991 (in Portuguese)
Acióly BM, Bedregal B (1997) A quasi-metric topology compatible with inclusion-monotonicity property on interval space. Reliab Comput 3(3):305–313
Dugundji J (1966) Topology. Allyn and Bacon Series in Advanced Mathematics, 9 edn. Allyn and Bacon, Boston
Gierz G et al (2003) Continuous lattices and domains. Cambridge University Press, Cambridge
Hickey T, Ju Q, Van Emdem MH (2001) Interval arithmetic: from principles to implementation. J ACM 48(5):1038–1068
Kahan WM (1968) A more complete interval arithmetic. Technical report, University of Michigan. Lecture Notes for A Summer Course at University of Michigan
Kearfott RB (1996) Rigorous global search: continuous problems, vol 13 of nonconvex optimization and its applications. Kluwer Academic Press, Dordrecht
Moore RE (1962) Interval arithmetic and automatic error analysis in digital computing. PhD thesis, Department of Mathematics, Stanford University, Stanford, California, Nov 1962. Published as Applied Mathematics and Statistics Laboratories Technical Report No. 25
Moore RE (1979) Methods and applications of interval analysis. SIAM, Philadelphia
de Santana FL, Santiago RHN (2013) Interval metrics, topology and continuous functions, computational and applied mathematics. Springer, Berlin (to appear)
Santiago RHN, Bedregal BRC, Acióly BM (2005) Comparing continuity of interval functions based on Moore and Scott topologies. Electron J Math Comput 2(1):1–14
Santiago RHN, Bedregal BRC, Acióly BM (2006) Formal aspects of correctness and optimality in interval computations. Form Asp Comput 18(2):231–243. Springer, Berlin
Santiago RHN, Bedregal BRC, Acióly BM (2004) Interval representations. Tend Mat Apl Comput 5(2):315–324
Scott DS (1970) Outline of a mathematical theory of computation. In: Proceedings of Fourth Annual Princeton Conference on Information Science and Systems, pp 169–176
Sieradski AJ (1992) Introduction to topology and homotopy. PWS-KENT Publishing Company, Boston
Smyth MB (1992) Topology. In: Abramsky S, Maibaum TSE (eds) Handbook of logic in computer science, vol 1, pp 641–761. Claredon Press, Oxford
Stoltenberg-Hansen V, Lindström I, Griffer ER (1994) Mathematical theory of domains. Cambridge tracts in theoretical computer science. Cambridge University Press, Cambridge
Trindade RMP, Bedregal BRC, Dória Neto AD, Acióly BM (2010) An interval metric. In: Lazinica A (ed) New advanced technologies. InTech, Vienna, pp 323–340
Acknowledgments
This work was partially supported by Brazilian Research Council (CNPq) under the processes numbers 306876/2012-4, 307681/2012-2 and 480832/2011-0.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Renata Hax Reiser Sander.
The partial results described in this paper were previously presented in IntMath TDS at CNMAC 2010-SBMAC honoring Prof. Dalcidio Claudio and his leadership over more than 40 years of Interval Mathematics research in Brazil.
Rights and permissions
About this article
Cite this article
Bedregal, B., Santiago, R. Some continuity notions for interval functions and representation. Comp. Appl. Math. 32, 435–446 (2013). https://doi.org/10.1007/s40314-013-0049-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40314-013-0049-z





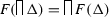 .
.