Skip to main content
SpringerLink
Log in

Generalized Jacobi–Galerkin method for nonlinear fractional differential algebraic equations

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

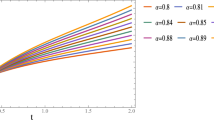
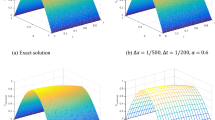
Abstract

In this paper, we provide an approximate approach based on the Galerkin method to solve a class of nonlinear fractional differential algebraic equations. The fractional derivative operator in the Caputo sense is utilized and the generalized Jacobi functions are employed as trial functions. The existence and uniqueness theorem as well as the asymptotic behavior of the exact solution are provided. It is shown that some derivatives of the solutions typically have singularity at origin dependence on the order of the fractional derivative. The influence of the perturbed data on the exact solutions along with the convergence analysis of the proposed scheme is also established. Some illustrative examples provided to demonstrate that this novel scheme is computationally efficient and accurate.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  • Atkinson KE, Han W (2009) Theoretical numerical analysis, a functional analysis framework, 3rd edn, Texts in Applied Mathematics, vol 39. Springer, Dordrecht

    Google Scholar 

  • Babaei A, Banihashemi S (2017) A stable numerical approach to solve a time-fractional inverse heat conduction problem. Iran J Sci Technol Trans A Sci. https://doi.org/10.1007/s40995-017-0360-4

    Google Scholar 

  • Bhrawy AH, Zaky MA (2016a) Shifted fractional-order Jacobi orthogonal functions: application to a system of fractional differential equations. Appl Math Model 40(2):832–845

  • Bhrawy AH, Zaky MA (2016b) A fractional-order Jacobi–Tau method for a class of time-fractional PDEs with variable coefficients. Math Methods Appl Sci 39(7):1765–1779

  • Canuto C, Hussaini MY, Quarteroni A, Zang TA (2006) Spectral methods. Fundamentals in single domains. Springer, Berlin

    MATH  Google Scholar 

  • Chen S, Shen J, Wang LL (2016) Generalized Jacobi functions and their applications to fractional differential equations. Math Comput 85:1603–1638

    Article  MathSciNet  MATH  Google Scholar 

  • Dabiri A, Butcher EA (2016) Numerical solution of multi-order fractional differential equations with multiple delays via spectral collocation methods. Appl Math Model 56:424–448

    Article  MathSciNet  Google Scholar 

  • Dabiri A, Butcher EA (2017a) Efficient modified Chebyshev differentiation matrices for fractional differential equations. Commun Nonlinear Sci Numer Simul 50:284–310

  • Dabiri A, Butcher EA (2017b) Stable fractional Chebyshev differentiation matrix for the numerical solution of multi-order fractional differential equations. Nonlinear Dyn 90(1):185–201

  • Dabiri A, Nazari M, Butcher EA (2016) Optimal fractional state feedback control for linear fractional periodic time-delayed systems. In: 2016 American control conference (ACC). https://doi.org/10.1109/acc.2016.7525339

  • Dabiri A, Moghaddam BP, Tenreiro Machadoc JA (2018) Optimal variable-order fractional PID controllers for dynamical systems. J Comput Appl Math 339:40–48

    Article  MathSciNet  MATH  Google Scholar 

  • Damarla SK, Kundu M (2015) Numerical solution of fractional order differential algebraic equations using generalized triangular function operational matrices. J Fract Calc Appl 6(2):31–52

    MathSciNet  MATH  Google Scholar 

  • Diethelm K (2010) The analysis of fractional differential equations. Springer, Berlin

    Book  MATH  Google Scholar 

  • Ding XL, Jiang YL (2014) Waveform relaxation method for fractional differential algebraic equations. Fract Calc Appl Anal 17(3):585–604

    Article  MathSciNet  MATH  Google Scholar 

  • Fletcher R (1987) Practical methods of optimization, 2nd edn. Wiley, New York

    MATH  Google Scholar 

  • Ghoreishi F, Mokhtary P (2014) Spectral collocation method for multi-order fractional differential equations. Int J Comput Methods 11:23. https://doi.org/10.1142/S0219876213500722

    Article  MathSciNet  MATH  Google Scholar 

  • Gear CW (1990) Differential algebraic equations, indices, and integral algebraic equations. SIAM J Numer Anal 27(6):1527–1534

    Article  MathSciNet  MATH  Google Scholar 

  • Hairer E, Lubich C, Roche M (1989) The numerical solution of differential-algebraic systems by Runge–Kutta methods. Springer, Berlin

    Book  MATH  Google Scholar 

  • Hesthaven JS, Gottlieb S, Gottlieb D (2007) Spectral methods for time-dependent problems, Cambridge Monographs on Applied and Computational Mathematics, vol 21. Cambridge University Press, Cambridge

    MATH  Google Scholar 

  • İbis B, Bayram M (2011) Numerical comparison of methods for solving fractional differential-algebraic equations (FDAEs). Comput Math Appl 62(8):3270–3278

    Article  MathSciNet  MATH  Google Scholar 

  • İbis B, Bayram M, Göksel Ağargün A (2011) Applications of fractional differential transform method to fractional differential-algebraic equations. Eur J Pure Appl Math 4(2):129–141

    MathSciNet  MATH  Google Scholar 

  • Jaradat HM, Zurigat M, Al-Sharan S (2014) Toward a new algorithm for systems of fractional differential algebraic equations. Ital J Pure Appl Math 32:579–594

    MATH  Google Scholar 

  • Kilbas AA, Srivastava HM, Trujillo JJ (2006) Theory and applications of fractional differential equations. Elsevier, Amsterdam

    MATH  Google Scholar 

  • Keshi FK, Moghaddam BP, Aghili A (2018) A numerical approach for solving a class of variable-order fractional functional integral equations. Comput Appl Math. https://doi.org/10.1007/s40314-018-0604-8

    Google Scholar 

  • Moghaddam BP, Aghili A (2012) A numerical method for solving linear non-homogeneous fractional ordinary differential equations. Appl Math Inf Sci 6(3):441–445

    MathSciNet  Google Scholar 

  • Moghaddam BP, Machado JAT (2017a) A computational approach for the solution of a class of variable-order fractional integro-differential equations with weakly singular kernels. Fract Calc Appl Anal 20(4):1305–1312. https://doi.org/10.1515/fca-2017-0053

  • Moghaddam BP, Machado JAT (2017b) SM-Algorithms for approximating the variable-order fractional derivative of high order. Fundam Inform 151(1–4):293–311

  • Moghaddam BP, Machado JAT, Behforooz HB (2017a) An integro quadratic spline approach for a class of variable order fractional initial value problems. Chaos Solitons Fractals 102:354–360

  • Moghaddam BP, Machado JAT, Babaei A (2017b) A computationally efficient method for tempered fractional differential equations with application. Appl Math Comput. https://doi.org/10.1007/s40314-017-0522-1

  • Mokhtary P (2015) Reconstruction of exponentially rate of convergence to Legendre collocation solution of a class of fractional integro-differential equations. J Comput Appl Math 279:145–158

    Article  MathSciNet  MATH  Google Scholar 

  • Mokhtary P (2016a) Discrete Galerkin method for fractional integro-differential equations. Acta Math Sci 36B(2):560–578

  • Mokhtary P (2016b) Numerical treatment of a well-posed Chebyshev Tau method for Bagley–Torvik equation with high-order of accuracy. Numer Algorithms 72:875–891

  • Mokhtary P (2017) Numerical analysis of an operational Jacobi Tau method forfractional weakly singular integro-differential equations. Appl Numer Math 121:52–67

    Article  MathSciNet  MATH  Google Scholar 

  • Mokhtary P, Ghoreishi F (2011) The \(L^2\)-convergence of the Legendre-spectral Tau matrix formulation for nonlinear fractional integro-differential equations. Numer Algorithms 58:475–496

    Article  MathSciNet  MATH  Google Scholar 

  • Mokhtary P, Ghoreishi F (2014a) Convergence analysis of the operational Tau method for Abel-type Volterra integral equations. Electron Trans Numer Anal 41:289–305

  • Mokhtary P, Ghoreishi F (2014b) Convergence analysis of spectral Tau method for fractional Riccati differential equations. Bull Iran Math Soc 40(5):1275–1296

  • Mokhtary P, Ghoreishi F, Srivastava HM (2016) The Müntz–Legendre Tau method for fractional differential equations. Appl Math Model 40(2):671–684

    Article  MathSciNet  Google Scholar 

  • Pedas A, Tamme E, Vikerpuur M (2016) Spline collocation for fractional weakly singular integro-differential equations. Appl Numer Math 110:204–214

    Article  MathSciNet  MATH  Google Scholar 

  • Podlubny I (1999) Fractional differential equations. Academic Press, New York

    MATH  Google Scholar 

  • Shen J, Tang T, Wang LL (2006) Spectral methods algorithms, analysis and applications. J Math Anal Appl 313:251–261

    Article  MathSciNet  Google Scholar 

  • Taghavi A, Babaei A, Mohammadpour A (2017) A stable numerical scheme for a time fractional inverse parabolic equations. Inverse Probl Sci Eng 25(10):1474–1491

    Article  MathSciNet  MATH  Google Scholar 

  • Zaky MA (2017) A Legendre spectral quadrature Tau method for the multi-term time-fractional diffusion equations. Appl Math Comput. https://doi.org/10.1007/s40314-017-0530-1

    Google Scholar 

  • Zhang W, Ge SS (2011) A global implicit function theorem without initial point and its applications to control of non-affine systems of high dimensions. Springer, Berlin

    Google Scholar 

  • Zurigat M, Momani S, Alawneha A (2010) Analytical approximate solutions of systems of fractional algebraic differential equations by homotopy analysis method. Comput Math Appl 59(3):1227–1235

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors cordially thank anonymous referees for their valuable comments that improved the quality of this paper.

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Basic Sciences, Sahand University of Technology, Tabriz, Iran

    F. Ghanbari, K. Ghanbari & P. Mokhtary

Authors
  1. F. Ghanbari
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. K. Ghanbari
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. P. Mokhtary
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to P. Mokhtary.

Additional information

Communicated by Vasily E. Tarasov.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ghanbari, F., Ghanbari, K. & Mokhtary, P. Generalized Jacobi–Galerkin method for nonlinear fractional differential algebraic equations. Comp. Appl. Math. 37, 5456–5475 (2018). https://doi.org/10.1007/s40314-018-0645-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40314-018-0645-z

Keywords

Mathematics Subject Classification

Search

Navigation