An intuitionistic fuzzy $(\delta , \gamma )$-norm entropy with its application in supplier selection problem

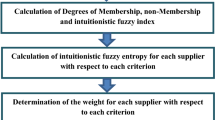
Abstract

In this communication, based on the concept of $(\delta , \gamma )$-norm entropy, an $(\delta , \gamma )$-norm intuitionistic fuzzy entropy measure is introduced in the settings of intuitionistic fuzzy set theory. Some of its major properties are also proved. The performance of the proposed entropy measure is demonstrated using numerical examples. Based on the proposed intuitionistic fuzzy (IF) entropy, a new multiple-attribute decision-making method (MADM) considering the merits of subjective and objective weights has been introduced. Two methods of finding the weights of attributes are discussed. The proposed MADM method is effectively explained with the help of supplier selection example.

Appendix: proofs of properties

Proof of Theorem 3.2

Bifurcate $X=\{q_1, q_2, \ldots , q_n\}$ into two parts $X_1$ and $X_2$, such that

$$\begin{aligned} X_1=\{q_i\in X:J\subseteq K\},\quad X_2=\{q_i\in X: J\supseteq K\}. \end{aligned}$$

(7.1)

This implies that for all $q_i\in X_1$,

$$\begin{aligned} \mu _J (q_i)\le \mu _K (q_i),\quad \nu _J (q_i)\ge \nu _K (q_i), \end{aligned}$$

(7.2)

and for all $q_i\in X_2$,

$$\begin{aligned} \mu _J (q_i)\ge \mu _K (q_i),\quad \nu _J (q_i)\le \nu _K (q_i). \end{aligned}$$

(7.3)

Using (3.5), we have

$$\begin{aligned}&E_\delta ^\gamma (J\cup K) =\frac{1}{n\left( 2^\frac{1-\delta }{\delta } -2^\frac{1-\gamma }{\gamma }\right) } \nonumber \\&\qquad \sum _{i=1}^n\Bigg \{\Big [(\mu _{J\cup K} (q_i)^\delta +\nu _{J\cup K} (q_i)^\delta )\times (\mu _{J\cup K} (q_i)+\nu _{J\cup K} (q_i))^{1-\delta }+2^{1-\delta }\pi _{J\cup K} (q_i)\Big ]^\frac{1}{\delta }\nonumber \\&\qquad -\Big [(\mu _{J\cup K} (q_i)^\gamma +\nu _{J\cup K} (q_i)^\gamma )\times (\mu _{J\cup K} (q_i)+\nu _{J\cup K} (q_i))^{1-\gamma }+2^{1-\gamma }\pi _{J\cup K} (q_i)\Big ]^\frac{1}{\gamma }\Bigg \};\nonumber \\&\quad =\frac{1}{n\left( 2^\frac{1-\delta }{\delta }-2^\frac{1-\gamma }{\gamma }\right) } \nonumber \\&\qquad \Bigg \{\sum _{X_1}\Bigg (\Big [(\mu _K (q_i)^\delta +\nu _K (q_i)^\delta )\times (\mu _K (q_i)+\nu _K (q_i))^{1-\delta }+2^{1-\delta }\pi _K (q_i)\Big ]^\frac{1}{\delta }\nonumber \\&\qquad -\Big [(\mu _K (q_i)^\gamma +\nu _K (q_i)^\gamma )\times (\mu _K (q_i)+\nu _K (q_i))^{1-\gamma }+2^{1-\gamma }\pi _K (q_i)\Big ]^\frac{1}{\gamma }\Bigg )\nonumber \\&\qquad +\sum _{X_2}\Bigg (\Big [(\mu _J (q_i)^\delta +\nu _J (q_i)^\delta )\times (\mu _J (q_i)+\nu _J (q_i))^{1-\delta }+2^{1-\delta }\pi _J (q_i)\Big ]^\frac{1}{\delta }\nonumber \\&\qquad -\Big [(\mu _J (q_i)^\gamma +\nu _J (q_i)^\gamma )\times (\mu _J (q_i)+\nu _J (q_i))^{1-\gamma }+2^{1-\gamma }\pi _J (q_i)\Big ]^\frac{1}{\gamma }\Bigg )\Bigg \}. \end{aligned}$$

(7.4)

Similarly,

$$\begin{aligned} E_\delta ^\gamma (J\cap K)&=\frac{1}{n\left( 2^\frac{1-\delta }{\delta } -2^\frac{1-\gamma }{\gamma }\right) }\nonumber \\&\quad \Bigg \{\sum _{X_1}\Bigg (\Big [(\mu _J (q_i)^\delta +\nu _J (q_i)^\delta )\times (\mu _J (q_i)+\nu _J (q_i))^{1-\delta }+2^{1-\delta }\pi _J (q_i)\Big ]^\frac{1}{\delta }\nonumber \\&\quad -\Big [(\mu _J (q_i)^\gamma +\nu _J (q_i)^\gamma )\times (\mu _J (q_i)+\nu _J (q_i))^{1-\gamma }+2^{1-\gamma }\pi _J (q_i)\Big ]^\frac{1}{\gamma }\Bigg )\nonumber \\&\quad +\sum _{X_2}\Bigg (\Big [(\mu _K (q_i)^\delta +\nu _K (q_i)^\delta )\times (\mu _K (q_i)+\nu _K (q_i))^{1-\delta }+2^{1-\delta }\pi _K (q_i)\Big ]^\frac{1}{\delta }\nonumber \\&\quad -\Big [(\mu _K (q_i)^\gamma +\nu _K (q_i)^\gamma )\times (\mu _K (q_i)+\nu _K (q_i))^{1-\gamma }+2^{1-\gamma }\pi _K (q_i)\Big ]^\frac{1}{\gamma }\Bigg )\Bigg \}. \end{aligned}$$

(7.5)

From (7.4) and (7.5),

$$\begin{aligned} E_\delta ^\gamma (J\cup K)+E_\delta ^\gamma (J\cap K)=E_\delta ^\gamma (J)+E_\delta ^\gamma (K). \end{aligned}$$

(7.6)

This proves the theorem. $\square$

Proof of Theorem 3.3

Proof of Theorem 3.3 follows directly from the proofs of Properties E1 and E2. $\square$