Skip to main content
SpringerLink
Log in

Non-intrusive polynomial chaos expansion for topology optimization using polygonal meshes

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

This paper deals with the applications of stochastic spectral methods for structural topology optimization in the presence of uncertainties. A non-intrusive polynomial chaos expansion is integrated into a topology optimization algorithm to calculate low-order statistical moments of the mechanical–mathematical model response. This procedure, known as robust topology optimization, can optimize the mean of the compliance while simultaneously minimizing its standard deviation. In order to address possible variabilities in the loads applied to the mechanical system of interest, magnitude and direction of the external forces are assumed to be uncertain. In this probabilistic framework, forces are described as a random field or a set of random variables. Representation of the random objects and propagation of load uncertainties through the model are efficiently done through Karhunen–Loève and polynomial chaos expansions. We take advantage of using polygonal elements, which have been shown to be effective in suppressing checkerboard patterns and reducing mesh dependency in the solution of topology optimization problems. Accuracy and applicability of the proposed methodology are demonstrated by means of several topology optimization examples. The obtained results, which are in excellent agreement with reference solutions computed via Monte Carlo method, show that load uncertainties play an important role in optimal design of structural systems, so that they must be taken into account to ensure a reliable optimization process.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

(adapted from [8])

Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Notes

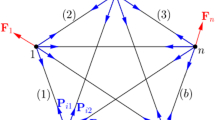
  1. These numerical realizations are defined in a computational mesh \({\textbf{x}}_1,{\textbf{x}}_2,\ldots ,{\textbf{x}}_n\).

References

  1. Andreasen CS, Sigmund O (2013) Topology optimization of fluid–structure-interaction problems in poroelasticity. Comput Methods Appl Mech Eng 258:55–62. https://doi.org/10.1016/j.cma.2013.02.007

    Article  MathSciNet  MATH  Google Scholar 

  2. Antonietti P, Bruggi M, Scacchi S, Verani M (2017) On the virtual element method for topology optimization on polygonal meshes: a numerical study. Comput Math Appl 74(5):1091–1109. https://doi.org/10.1016/j.camwa.2017.05.025 (SI: SDS2016—Methods for PDEs)

    Article  MathSciNet  MATH  Google Scholar 

  3. Asadpoure A, Tootkabonia M, Guest J (2011) Robust topology optimization of structures with uncertainties in stiffness—application to truss structures. Comput Struct 89:1031–1041. https://doi.org/10.1016/j.compstruc.2010.11.004

    Article  Google Scholar 

  4. Atkinson KE (2009) The numerical solution of integral equations of the second kind, reissue edn. Cambridge University Press, Cambridge

    MATH  Google Scholar 

  5. Banichuk N, Neittaanmäki P (2010) Structural optimization with uncertainties. Springer, Dordrecht

    Book  Google Scholar 

  6. Bellizzi S, Sampaio R (2012) Smooth decomposition of random fields. J Sound Vib 331:3509–3520. https://doi.org/10.1016/j.jsv.2012.03.030

    Article  Google Scholar 

  7. Bendsøe MP, Kikuchi N (1988) Generating optimal topologies in structural design using a homogenization method. Comput Methods Appl Mech Eng 71:197–224

    Article  MathSciNet  Google Scholar 

  8. Bendsøe MP, Sigmund O (2004) Topology optimization: theory, methods, and applications. Springer, Berlin

    Book  Google Scholar 

  9. Betz W, Papaioannou I, Straub D (2014) Numerical methods for the discretization of random fields by means of the Karhunen–Loève expansion. Comput Methods Appl Mech Eng 271:109–129. https://doi.org/10.1016/j.cma.2013.12.010

    Article  MATH  Google Scholar 

  10. Beyer HG, Sendhoff B (2007) Robust optimization—a comprehensive survey. Comput Methods Appl Mech Eng 196:3190–3218. https://doi.org/10.1016/j.cma.2007.03.003

    Article  MathSciNet  MATH  Google Scholar 

  11. Birge J, Louveaux F (2011) Introduction to stochastic programming. Springer, New York

    Book  Google Scholar 

  12. Brezis H (2010) Functional analysis, Sobolev spaces and partial differential equations. Springer, New York

    Book  Google Scholar 

  13. Bruggi M (2008) On the solution of the checkerboard problem in mixed-FEM topology optimization. Comput Struct 86:1819–1829. https://doi.org/10.1016/j.compstruc.2008.04.008

    Article  Google Scholar 

  14. Chen S, Chen W, Lee S (2010) Level set based robust shape and topology optimization under random field uncertainties. Struct Multidiscip Optim 41:507–524. https://doi.org/10.1007/s00158-009-0449-2

    Article  MathSciNet  MATH  Google Scholar 

  15. Ciarlet PG (2013) Linear and nonlinear functional analysis with applications. SIAM, Philadelphia

    MATH  Google Scholar 

  16. da Silva G, Cardoso E (2017) Stress-based topology optimization of continuum structures under uncertainties. Comput Methods Appl Mech Eng 313:647–672. https://doi.org/10.1016/j.cma.2016.09.049

    Article  MathSciNet  Google Scholar 

  17. Dapogny C, Faure A, Michailidis G, Allaire G, Couvelas A, Estevez R (2017) Geometric constraints for shape and topology optimization in architectural design. Comput Mech 59:933–965. https://doi.org/10.1007/s00466-017-1383-6

    Article  MathSciNet  MATH  Google Scholar 

  18. Doltsinis I, Kang Z (2004) Robust design of structures using optimization methods. Comput Methods Appl Mech Eng 193(23):2221–2237. https://doi.org/10.1016/j.cma.2003.12.055

    Article  MATH  Google Scholar 

  19. Duan XB, Li FF, Qin XQ (2015) Adaptive mesh method for topology optimization of fluid flow. Appl Math Lett 44:40–44. https://doi.org/10.1016/j.aml.2014.12.016

    Article  MathSciNet  MATH  Google Scholar 

  20. Dunning PD, Kim HA (2013) Robust topology optimization: minimization of expected and variance of compliance. AIAA J 51:2656–2664. https://doi.org/10.2514/1.J052183

    Article  Google Scholar 

  21. Eldred M (2009) Recent advances in non-intrusive polynomial chaos and stochastic collocation methods for uncertainty analysis and design. In: 50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. https://doi.org/10.2514/6.2009-2274

  22. Ghanem R (1999) Ingredients for a general purpose stochastic finite elements implementation. Comput Methods Appl Mech Eng 168:19–34. https://doi.org/10.1016/S0045-7825(98)00106-6

    Article  MathSciNet  MATH  Google Scholar 

  23. Ghanem R, Red-Horse J (2017) Polynomial chaos: modeling, estimation, and approximation. Springer, Berlin, pp 521–551

    Google Scholar 

  24. Ghanem RG, Spanos PD (2003) Stochastic finite elements: a spectral approach, 2nd edn. Dover, New York

    MATH  Google Scholar 

  25. Guest JK, Igusa T (2008) Structural optimization under uncertain loads and nodal locations. Comput Methods Appl Mech Eng 198:116–124. https://doi.org/10.1016/j.cma.2008.04.009

    Article  MathSciNet  MATH  Google Scholar 

  26. Hoshina TYS, Menezes IFM, Pereira A (2018) A simple adaptive mesh refinement scheme for topology optimization using polygonal meshes. J Braz Soc Mech Sci Eng 40(7):348. https://doi.org/10.1007/s40430-018-1267-5

    Article  Google Scholar 

  27. Jalalpour M, Guest JK, Igusa T (2013) Reliability-based topology optimization of trusses with stochastic stiffness. Struct Saf 43:41–49. https://doi.org/10.1016/j.strusafe.2013.02.003

    Article  Google Scholar 

  28. Keshavarzzadeh V, Fernandez F, Tortorelli DA (2017) Topology optimization under uncertainty via non-intrusive polynomial chaos expansion. Comput Methods Appl Mech Eng 318:120–147. https://doi.org/10.1016/j.cma.2017.01.019

    Article  MathSciNet  Google Scholar 

  29. Kim NH, Wang H, Queipo NV (2006) Efficient shape optimization under uncertainty using polynomial chaos expansions and local sensitivities. AIAA J 44:1112–1116. https://doi.org/10.2514/1.13011

    Article  Google Scholar 

  30. Kroese DP, Taimre T, Botev ZI (2011) Handbook of Monte Carlo methods. Wiley, London

    Book  Google Scholar 

  31. Kundu A, Adhikari S, Friswell M (2014) Stochastic finite elements of discretely parameterized random systems on domains with boundary uncertainty. Int J Numer Methods Eng 100(3):183–221

    Article  MathSciNet  Google Scholar 

  32. Kundu A, Matthies H, Friswell M (2018) Probabilistic optimization of engineering system with prescribed target design in a reduced parameter space. Comput Methods Appl Mech Eng 337:281–304

    Article  MathSciNet  Google Scholar 

  33. Luo Y, Niu Y, Li M, Kang Z (2017) A multi-material topology optimization approach for wrinkle-free design of cable-suspended membrane structures. Comput Mech 59:967–980. https://doi.org/10.1007/s00466-017-1387-2

    Article  MathSciNet  Google Scholar 

  34. Maître OPL, Knio OM (2010) Spectral methods for uncertainty quantification: with applications to computational fluid dynamics. Springer, Dordrecht

    Book  Google Scholar 

  35. Michell MCE (1904) LVIII. The limits of economy of material in frame-structures. Lond Edinb Dublin Philos Mag J Sci 8:589–597. https://doi.org/10.1080/14786440409463229

    Article  MATH  Google Scholar 

  36. Nanthakumar SS, Valizadeh N, Park HS, Rabczuk T (2015) Surface effects on shape and topology optimization of nanostructures. Comput Mech 56:97–112. https://doi.org/10.1007/s00466-015-1159-9

    Article  MathSciNet  MATH  Google Scholar 

  37. Nguyen-Xuan H (2017) A polytree-based adaptive polygonal finite element method for topology optimization. Int J Numer Methods Eng 110(10):972–1000. https://doi.org/10.1002/nme.5448

    Article  MathSciNet  Google Scholar 

  38. Park J, Sutradhar A, Shah JJ, Paulino GH (2018) Design of complex bone internal structure using topology optimization with perimeter control. Comput Biol Med. https://doi.org/10.1016/j.compbiomed.2018.01.001

    Article  Google Scholar 

  39. Pereira A, Talischi C, Paulino GH, Menezes IFM, Carvalho MS (2016) Fluid flow topology optimization in polytop: stability and computational implementation. Struct Multidiscip Optim 54:1345–1364. https://doi.org/10.1007/s00158-014-1182-z

    Article  MathSciNet  Google Scholar 

  40. Perrin G, Soize C, Duhamel D, Funfschilling C (2013) Karhunen–Loève expansion revisited for vector-valued random fields: scaling, errors and optimal basis. J Comput Phys 242:607–622. https://doi.org/10.1016/j.jcp.2013.02.036

    Article  MathSciNet  MATH  Google Scholar 

  41. Pettersson MP, Iaccarino G, Nordström J (2015) Polynomial chaos methods for hyperbolic partial differential equations: numerical techniques for fluid dynamics problems in the presence of uncertainties. Springer, Berlin

    Book  Google Scholar 

  42. Putek P, Pulch R, Bartel A, ter Maten EJW, Günther M, Gawrylczyk KM (2016) Shape and topology optimization of a permanent-magnet machine under uncertainties. J Math Ind 6:11. https://doi.org/10.1186/s13362-016-0032-6

    Article  MathSciNet  MATH  Google Scholar 

  43. Qizhi Q, Kang Z, Wang Y (2014) A topology optimization method for geometrically nonlinear structures with meshless analysis and independent density field interpolation. Comput Mech 54:629–644. https://doi.org/10.1007/s00466-014-1011-7

    Article  MathSciNet  MATH  Google Scholar 

  44. Richardson J, Filomeno Coelho R, Adriaenssens S (2016) A unified stochastic framework for robust topology optimization of continuum and truss-like structures. Eng Optim 48:334–350. https://doi.org/10.1080/0305215X.2015.1011152

    Article  MathSciNet  Google Scholar 

  45. Romero JS, Silva ECN (2014) A topology optimization approach applied to laminar flow machine rotor design. Comput Methods Appl Mech Eng 279:268–300. https://doi.org/10.1016/j.cma.2014.06.029

    Article  MathSciNet  MATH  Google Scholar 

  46. Rubinstein RY, Kroese DP (2016) Simulation and the Monte Carlo method, 3rd edn. Wiley, London

    Book  Google Scholar 

  47. Shin S, Samanlioglu F, Cho BR, Wiecek MM (2011) Computing trade-offs in robust design: perspectives of the mean squared error. Comput Ind Eng 60:248–255. https://doi.org/10.1016/j.cie.2010.11.006

    Article  Google Scholar 

  48. Sigmund O, Petersson J (1998) Numerical instabilities in topology optimization: a survey on procedures dealing with checkerboards, mesh-dependencies and local minima. Struct Optim 16:68–75. https://doi.org/10.1007/BF01214002

    Article  Google Scholar 

  49. Soize C (2013) Stochastic modeling of uncertainties in computational structural dynamics—recent theoretical advances. J Sound Vib 332:2379–2395. https://doi.org/10.1016/j.jsv.2011.10.010

    Article  Google Scholar 

  50. Soize C (2015) Polynomial chaos expansion of a multimodal random vector. SIAM/ASA J Uncertain Quantif 3:34–60. https://doi.org/10.1137/140968495

    Article  MathSciNet  MATH  Google Scholar 

  51. Soize C (2017) Uncertainty quantification: an accelerated course with advanced applications in computational engineering. Springer, Berlin

    Book  Google Scholar 

  52. Soize C, Desceliers C (2010) Computational aspects for constructing realizations of polynomial chaos in high dimension. SIAM J Sci Comput 32:2820–2831. https://doi.org/10.1137/100787830

    Article  MathSciNet  MATH  Google Scholar 

  53. Soize C, Ghanem R (2004) Physical systems with random uncertainties: chaos representations with arbitrary probability measure. SIAM J Sci Comput 26:395–410. https://doi.org/10.1137/S1064827503424505

    Article  MathSciNet  MATH  Google Scholar 

  54. Soize C, Ghanem R (2017) Polynomial chaos representation of databases on manifolds. J Comput Phys 335:201–221. https://doi.org/10.1016/j.jcp.2017.01.031

    Article  MathSciNet  MATH  Google Scholar 

  55. Spanos PD, Ghanem R (1989) Stochastic finite element expansion for random media. J Eng Mech 115:1035–1053. https://doi.org/10.1061/(ASCE)0733-9399(1989)115:5(1035)

    Article  Google Scholar 

  56. Stefanou G (2009) The stochastic finite element method: past, present and future. Comput Methods Appl Mech Eng 198:1031–1051. https://doi.org/10.1016/j.cma.2008.11.007

    Article  MATH  Google Scholar 

  57. Svanberg K (1987) The method of moving asymptotes—a new method for structural optimization. Int J Numer Methods Eng 24:359–373. https://doi.org/10.1002/nme.1620240207

    Article  MathSciNet  MATH  Google Scholar 

  58. Talischi C, Paulino GH, Pereira A, Menezes IFM (2010) Polygonal finite elements for topology optimization: a unifying paradigm. Int J Numer Methods Eng 82:671–698. https://doi.org/10.1002/nme.2763

    Article  MATH  Google Scholar 

  59. Talischi C, Paulino GH, Pereira A, Menezes IFM (2012) PolyTop: a Matlab implementation of a general topology optimization framework using unstructured polygonal finite element meshes. Struct Multidiscip Optim 45:329–357. https://doi.org/10.1007/s00158-011-0696-x

    Article  MathSciNet  MATH  Google Scholar 

  60. Tootkaboni M, Asadpoure A, Guest JK (2012) Topology optimization of continuum structures under uncertainty—a polynomial chaos approach. Comput Methods Appl Mech Eng 201–204:263–275. https://doi.org/10.1016/j.cma.2011.09.009

    Article  MathSciNet  MATH  Google Scholar 

  61. Wu J, Gao J, Luo Z, Brown T (2016) Robust topology optimization for structures under interval uncertainty. Adv Eng Softw 96:36–48. https://doi.org/10.1016/j.advengsoft.2016.05.002

    Article  Google Scholar 

  62. Xia L, Da D, Yvonnet J (2018) Topology optimization for maximizing the fracture resistance of quasi-brittle composites. Comput Methods Appl Mech Eng 332:234–254. https://doi.org/10.1016/j.cma.2017.12.021

    Article  MathSciNet  Google Scholar 

  63. Xiu D (2010) Numerical methods for stochastic computations: a spectral method approach. Princeton University Press, Princeton

    Book  Google Scholar 

  64. Xiu D, Karniadakis GE (2002) The Wiener–Askey polynomial chaos for stochastic differential equations. SIAM J Sci Comput 24:619–644. https://doi.org/10.1137/S1064827501387826

    Article  MathSciNet  MATH  Google Scholar 

  65. Zhang W, Kang Z (2017) Robust shape and topology optimization considering geometric uncertainties with stochastic level set perturbation. Int J Numer Methods Eng 110:31–56. https://doi.org/10.1002/nme.5344

    Article  MathSciNet  MATH  Google Scholar 

  66. Zhang XS, de Sturler E, Paulino GH (2017) Stochastic sampling for deterministic structural topology optimization with many load cases: density-based and ground structure approaches. Comput Methods Appl Mech Eng 325:463–487. https://doi.org/10.1016/j.cma.2017.06.035

    Article  MathSciNet  Google Scholar 

  67. Zhang XS, Paulino GH, Ramos AS (2018) Multi-material topology optimization with multiple volume constraints: a general approach applied to ground structures with material nonlinearity. Struct Multidiscip Optim 57:161–182. https://doi.org/10.1007/s00158-017-1768-3

    Article  MathSciNet  Google Scholar 

  68. Zhao J, Wang C (2014) Robust structural topology optimization under random field loading uncertainty. Struct Multidiscip Optim 50:517–522. https://doi.org/10.1007/s00158-014-1119-6

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

NC acknowledges the financial support from the Group of Technology in Computer Graphics (Tecgraf/PUC-Rio), Rio de Janeiro, Brazil. AP and IFMM acknowledge the financial support from the National Council for Scientific and Technological Development (CNPq) under projects 312280/2015-7 and 309708/2015-0, respectively. AP and ACJr are thankful for the support from Carlos Chagas Filho Research Foundation of Rio de Janeiro State (FAPERJ) under grants E-26/203.189/2016, E-26/010.002.178/2015 and E-26/010.000.805/2018. The information provided in this paper is the sole opinion of the authors and does not necessarily reflect the views of the sponsoring agencies..

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Pontifical Catholic University of Rio de Janeiro (PUC-Rio), Rua Marquês de São Vicente, 225, Rio de Janeiro, RJ, 22453-900, Brazil

    Nilton Cuellar, Anderson Pereira & Ivan F. M. Menezes

  2. Nucleus of Modeling and Experimentation with Computers (NUMERICO), Universidade do Estado do Rio de Janeiro (UERJ), Rua São Francisco Xavier, 524, Rio de Janeiro, RJ, 20550-900, Brazil

    Americo Cunha Jr.

Authors
  1. Nilton Cuellar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Anderson Pereira
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ivan F. M. Menezes
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Americo Cunha Jr.
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Anderson Pereira.

Additional information

Technical Editor: Paulo de Tarso Rocha de Mendonça, Ph.D.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cuellar, N., Pereira, A., Menezes, I.F.M. et al. Non-intrusive polynomial chaos expansion for topology optimization using polygonal meshes. J Braz. Soc. Mech. Sci. Eng. 40, 561 (2018). https://doi.org/10.1007/s40430-018-1464-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-018-1464-2

Keywords

Search

Navigation