1 Introduction

Today, laminated composite plates have many applications as advanced engineering materials, primarily as components in aircrafts, power plants, civil engineering structures, ships, cars, rail vehicles, robots, prosthetic devices, sports equipment etc. These engineering applications have motivated the interest of several researchers in introducing new mathematical models and investigating approaches to expectation of the nonlinear dynamics of physical systems in the case of large deformation [1–4].

Bose et al. [5] investigate vibration analysis of a rectangular thin isotropic plate with a part-through surface crack of arbitrary orientation and position using the Kirchhoff plate theory. Chang et al. [6] studied the bifurcations and chaos of a rectangular thin plate with 1:1 internal resonance. Zhang [7] investigated the local and global bifurcations of a rectangular thin plate under parametrical excitation by the analytical and numerical approaches when the averaged equations have one non-semisimple double zero and a pair of pure imaginary eigenvalues The method of multiple scales is used to obtain the averaged equations. The case of 1:1 internal resonance and primary parametric resonance are considered. Ikeda and Nakazawa [8] investigated the mechanism of the complex recursive bifurcation behaviour of a four-side simply supported rectangular plate. The bifurcation analysis of the plate was carried out to assess the validity of the rule and to demonstrate the merit of the block-diagonalization.

Ye et al. [9] investigated the local and global non-linear dynamics of a parametrically excited symmetric cross-ply composite laminated rectangular thin plate under parametric excitation. This study is focused on the case of 1:1 internal resonance and primary parametric resonance. Yeh [10] presents a novel analytical approach utilizing fractal dimension criteria and the maximum Lyapunov exponent to characterize the conditions, which can potentially lead to the chaotic motion of a simply supported thermo-mechanically coupled orthotropic rectangular plate undergoing large deflections. Guo et al. [11] analyzed the nonlinear oscillations and chaotic dynamics of a four-edge simply supported angle-ply composite laminated rectangular thin plate subjected to the in-plane and transverse loads. The asymptotic perturbation method is used to derive the four averaged equations under 1:1 internal resonance. Tien et al. [12] examined the weakly non-linear resonance response of a two-degree-of-freedom shallow arch subjected to simple harmonic excitation for the case of 1:2 internal resonances. The method of averaging is used to yield a set of autonomous equations of the first-order approximations to the response of the system.

Sayed and Mousa [13] investigated the influence of the quadratic and cubic terms on non-linear dynamic characteristics of the angle-ply composite laminated rectangular plate with parametric and external excitations. Two cases of the sub-harmonic resonances cases in the presence of 1:2 internal resonances are considered. The method of multiple time scale perturbation is applied to solve the nonlinear differential equations describing the system up to and including the second-order approximation. Sayed and Mousa [14] studied an analytical investigation of the nonlinear vibration of a symmetric cross-ply composite laminated piezoelectric rectangular plate under parametric and external excitations. Their study focused on the case of 1:1:3 primary resonances and internal resonance, and they verified the analytical results calculated by the method of multiple time scale by comparing them with the numerical results of the modal equations. The obtained result was verified by comparing the results of the finite difference method (FDM) and Runge-Kutta (RKM) method. Yeh et al. [15] presents a new approach to characterize the conditions that can possibly lead to chaotic motion for a simply supported large deflection rectangular plate of thermo-mechanical coupling by utilizing the criteria of the fractal dimension and the maximum Lyapunov exponent. Yao et al. [16] investigated the Shilnikov type multi-pulse orbits and chaotic dynamics of a four-edge simply supported laminated composite piezoelectric rectangular plate subjected to the in-plane, transverse and piezoelectric excitations by using the energy phase method. The method of multiple scales is utilized to obtain the four-dimensional averaged equation in the case of primary parametric resonance and 1:3 internal resonances

Zhang et al. [17] analyzed the Shilnikov type multi-pulse chaotic dynamics of a six-dimensional nonlinear system, which represents the averaged equation of a composite laminated piezoelectric rectangular plate subjected to the transverse, in-plane excitations and the excitation loaded by piezoelectric layers. The case of 1:2:4 internal resonances are considered. Zhang et al. [18] investigated the nonlinear vibrations and chaotic dynamics of the orthotropic functionally graded material (FGM) rectangular plate under combined transverse and in-plane excitations. The considered resonant case here is 1:2:4 internal resonance, and principal parametric resonance-subharmonic resonance of order 1/2. Zhang and Li [19] studied the chaotic motions of a buckled thin plate in the presence of resonance using exponential dichotomies and an averaging procedure. Guo and Feng-Ming [20], investigated the nonlinear vibration of a two-dimensional composite laminated plate in subsonic air flow. They found that the composite laminated plate with smaller ply angle exhibits more stable dynamic properties than that with larger ply angles. Feng-Ming and Guo [21] investigated the 1/3 subharmonic resonance of a composite laminated circular cylindrical shell with clamped boundary conditions at both ends in subsonic air flow under radial harmonic excitation. The method of multiple scales is used to analyzed the 1/3 subharmonic resonance of the shell and the sufficient and necessary conditions for the stability of the steady states is obtained by solving the eigenvalue problem of the linearized equations. Guo and Feng-Ming [22] investigated the bifurcation and chaotic motion of a two-dimensional (2D) composite laminated plate with geometric nonlinearity subjected to incompressible subsonic flow and transverse harmonic excitation. The effects of the flow velocity and the amplitude and angular frequency of the external excitation on the chaotic motion of the plate are analyzed.

Sayed [23] studied the analytical and numerical solutions of the coupled differential equations describing the response of an inclined cable subjected to external and parametric excitation forces. The stability of the system are studied by using frequency response equations and phase-plane method. Zhong et al. [24] obtained the analytically solution of non-dimensional differential equation of the motion, as well as coupled boundary conditions, are obtained using the method of multiple time scales. The obtained results of frequencies and mode shapes are compared with the cases of ideal boundary conditions, and the differences between them are contrasted on frequency response curves. Varadharajan and Rajendran [25] presented the closed analytical expressions for substrate and product concentrations of the coupled system of non-linear second-order reaction differential equation in basic enzyme reaction. The obtained results are compared with simulation results and are found to be in good agreement. Amer et al. [26] dealt with the dynamical system of a twin-tail aircraft under different controllers. They used two simple active control laws based on the linear negative velocity and acceleration feedback Sayed and Hamed [27] obtained the analytical and numerical solutions of coupled nonlinear differential equations describing the motion of pitch roll under parametric and harmonic excitations using multiple scale method. Sayed and Kamel [28, 29] investigated the effects of different controllers on the vibrating system and the saturation control to reduce vibrations due to rotor blade flapping motion. The method of multiple scales is used to obtain the analytical solution of the coupled second order differential equation. The stability of the obtained numerical solution is investigated using both phase-plane and frequency, force response curves.

Up to now, a few studies on the bifurcations and chaos of the composite laminated piezoelectric plate have been achieved. In this paper, the stability of the composite laminated piezoelectric rectangular plate under transverse and in-plane excitations simultaneous are investigated. The method of multiple scales is applied to obtain the second-order approximations. All possible resonance cases are deduced at this approximation. The study is focused on the case of 1:1 internal resonance and primary resonance. The stability of the system and the effects of different parameters on system behavior have been studied using frequency response curves. Variation of some parameters leads to multi-valued amplitudes and hence to jump phenomena. Some recommendations regarding the different parameters of the system are reported. A comparison with the available published work is reported.

2 Problem formulation

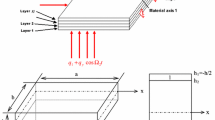
We consider a simply supported four edges composite laminated piezoelectric rectangular plate with side lengths \(a\) and \(b\) and thickness \(h\), as shown in Fig. 1. The laminated composite piezoelectric rectangular plate is considered as regular symmetric cross-ply laminates with \(n\) layers. The in-plane excitations are loaded along the \(y\) direction at \(x=0\) in the form \(q_x \cos \Omega _{1 } t\) and loaded along the \(x\) direction at \(y=0\) in the form \(q_y \cos \Omega _{2 } t\). The transverse excitation subjected to the composite laminated piezoelectric rectangular plate represented by \(q=q_3 \cos \Omega _{3 } t\) is out of plane excitation. The dynamic electrical loading is expressed as \(E_z =E_z \cos \Omega _{4 } t\). The nonlinear governing equations of motion for the composite laminated piezoelectric rectangular plate in a dimensionless form can be written as follows [16]:

$$\begin{aligned}&\!\!\!\ddot{u}_1 +{\upmu }_1 \dot{u}_1 +{\upomega }_1^2 u_1 +(f_{11} \cos \Omega _1 t+f_{12} \cos \Omega _2 t\nonumber \\&+\,f_{14} \cos \Omega _4 t)u_1 +{\upalpha }_1 u_1^2 u_2 +{\upalpha }_2 u_2^2 u_1 +{\upalpha }_3 u_1^3\nonumber \\&+\,{\upalpha }_4 u_2^3 =f_1 \cos \Omega _3 t, \end{aligned}$$
(1)
$$\begin{aligned}&\!\!\!\ddot{u}_2 +{\upmu }_2 \dot{u}_2 +{\upomega }_2^2 u_2 +(f_{21} \cos \Omega _1 t+f_{22} \cos \Omega _2 t\nonumber \\&+\,f_{24} \cos \Omega _4 t)u_2 +{\upbeta }_1 u_2^2 u_1 +{\upbeta }_2 u_1^2 u_2 +{\upbeta }_3 u_2^3\nonumber \\&+\,{\upbeta }_4 u_1^3 =f_2 \cos \Omega _3 t, \end{aligned}$$
(2)

where the dots indicate differentiation with respect to time, \(u_1\) and \(u_2\) are the vibration amplitudes of the composite laminated piezoelectric rectangular plate for the first-order and second-order modes, respectively, \({\upmu }_{1 }\)and \({\upmu }_{2}\) are the linear viscous damping coefficients, \(\upomega _1 \) and \(\upomega _2 \) are the linear natural frequencies of the rectangular plate, and \(\Omega _{1}, \Omega _{2}, \Omega _{3}\) and \(\Omega _{4 }\) are the excitations frequencies, \({\upalpha }_i, {\upbeta }_i (i=1,2,3,4)\) are the non-linear coefficients.

Fig. 1
figure 1

The model of a laminated composite piezoelectric rectangular plate

Full size image

\(f_{n1}, f_{n2}, f_{n4}\) and \(f_n (n =1, 2)\) are the amplitudes of parametric and external excitation forces corresponding to the three non-linear modes. The linear viscous damping and exciting forces are assumed to be

$$\begin{aligned}&\!\!\!{\upmu }_n ={\upvarepsilon } \hat{{{\upmu } }}_n, f_{n1} ={\upvarepsilon } \hat{{f}}_{n1}, f_{n2} ={\upvarepsilon } \hat{{f}}_{n2},\nonumber \\&\quad \qquad f_{n4} ={\upvarepsilon } \hat{{f}}_{n4}, f_n ={\upvarepsilon }^{2} \hat{{f}}_n \qquad n=1, 2, \end{aligned}$$
(3)

where \({\upvarepsilon } \) is a small perturbation parameter and \(0<{\upvarepsilon } <<1\).

The external excitation forces \(\hat{{f}}_n \) are of the order 2 and the linear viscous damping \(\hat{{\upmu }}_n \), parametric exciting forces \(\hat{{f}}_{n1}, \hat{{f}}_{n2}, \hat{{f}}_{n4}\) are of the order 1. To consider the influence of the cubic terms on non-linear dynamic characteristics of the composite laminated piezoelectric rectangular plate, we need to obtain the second-order approximate solution of Eqs. (1) and (2).

3 Perturbation analysis

The method of multiple scales [30–32] is applied to obtain a second-order approximation for the system, which is a powerful tool in determining periodic solutions of small amplitude. We seek an approximate solution of Eqs. (1) and (2) in the form

$$\begin{aligned}&\!\!\!\!u_n (t, {\upvarepsilon })={\upvarepsilon } u_{n1} (T_0, T_1, T_2)+{\upvarepsilon }^{2} u_{n2} (T_0, T_1, T_2)\nonumber \\&+\,{\upvarepsilon }^{3} u_{n3} (T_0, T_1, T_2) +O({\upvarepsilon }^{4}), \quad n=1, 2. \end{aligned}$$
(4)

where \(T_0 =t\) is a fast time scale associated with changes occurring at the frequencies \(\upomega _n \) and \(\Omega _{1}, \Omega _{2}, \Omega _{3}\) and \(\Omega _{4 }\) and \(T_1 ={\upvarepsilon } t,T_2 ={\upvarepsilon }^{2}t\) are slow time scales associated with modulations in the amplitudes and phases caused by the non-linearity, damping, and resonances. In terms of \(T_0, T_1, T_2 \) the time derivatives can be expressed as the following:

$$\begin{aligned}&\!\!\!\frac{d}{dt}=\frac{\partial }{\partial T_0 }+{\upvarepsilon } \frac{\partial }{\partial T_1 }+{\upvarepsilon }^{2}\frac{\partial }{\partial T_2 }=D_0 +{\upvarepsilon } D_1 +{\upvarepsilon }^{2} D_2, \end{aligned}$$
(5)
$$\begin{aligned}&\!\!\!\frac{d^{2}}{dt^{2}}=D_0^2 +2{\upvarepsilon } D_0 D_1 +{\upvarepsilon }^{2}(D_1^2 +2D_0 D_2), \end{aligned}$$
(6)

where \(D_n =\partial /{\partial T_n }\). Substituting Eqs. (3) and (4)–(6) into Eqs. (1)–(2) and equating the coefficients of like powers of \({\upvarepsilon }\), we obtain the following

$$\begin{aligned}&\!\!\!O({\upvarepsilon }):({D_0^{2} }+{\upomega }_1^{2}) u_{11} =0,\end{aligned}$$
(7)
$$\begin{aligned}&\!\!\!({D_0^{2}} +{\upomega }_2^{2}) u_{21} =0,\end{aligned}$$
(8)
$$\begin{aligned}&\!\!\!\!O({\upvarepsilon }^{2}):({D_0^{2}} +{\upomega }_1^{2}) u_{12} = {-2D_{0}} {D_{1}} u_{11} -\hat{{\upmu }}_1 D_0 u_{11}\nonumber \\&\!\!\!\quad -\,\,(\hat{{f}}_{11} \cos \Omega _{1} T_{0} +\hat{{f}}_{12} \cos \Omega _2 T_0\nonumber \\&\!\!\!\quad +\,\,\hat{{f}}_{14} \cos \Omega _4 T_0)u_{11} +\hat{{f}}_1 \cos \Omega _{3} T_0, \end{aligned}$$
(9)
$$\begin{aligned}&\!\!\!({D_0^{2}} +{\upomega }_2^2)u_{22}={-2D_{0}} {D_{1}} u_{21} -\hat{{\upmu }}_2 D_0 u_{21}\nonumber \\&\!\!\!\quad -(\hat{{f}}_{21} \cos \Omega _1 T_0 +\hat{{f}}_{22} \cos \Omega _2 T_0 \nonumber \\&\!\!\!\quad +\,\,\hat{{f}}_{24} \cos \Omega _4 T_0)u_{21} +\hat{{f}}_2 \cos \Omega _{3 } T_0, \end{aligned}$$
(10)
$$\begin{aligned}&\!\!\!O({\upvarepsilon }^{3}):(D_0^2 +{\upomega }_1^2) u_{13} =-D_1^2 u_{11} -2D_0 D_2 u_{11}\nonumber \\&\!\!\!\quad -\,\,2D_0 D_1 u_{12} -\hat{{\upmu }}_1 (D_0 u_{12} +D_1 u_{11})\nonumber \\&\!\!\!\quad -\,\,(\hat{{f}}_{11} \cos \Omega _1 T_0 +\hat{{f}}_{12} \cos \Omega _2 T_0 +\hat{{f}}_{14} \cos \Omega _4 T_0)u_{12}\nonumber \\&\!\!\!\quad -\,\,{\upalpha }_1 u_{11}^2 u_{21} -{\upalpha }_2 u_{21}^2 u_{11} -{\upalpha }_3 u_{11}^3 -{\upalpha }_4 u_{21}^3, \end{aligned}$$
(11)
$$\begin{aligned}&\!\!\!(D_0^2 +{\upomega }_2^2) u_{23} =-D_1^2 u_{21} -2D_0 D_2 u_{21}\nonumber \\&\!\!\!\quad -\,\,2D_0 D_1 u_{22} -\hat{{\upmu }}_2 (D_0 u_{22} +D_1 u_{21})\nonumber \\&\!\!\!\quad -\,\,(\hat{{f}}_{21} \cos \Omega _1 T_0 +\hat{{f}}_{22} \cos \Omega _2 T_0\nonumber \\&\!\!\!\quad +\,\,\hat{{f}}_{24} \cos \Omega _4 T_0)u_{22} -{\upbeta }_1 u_{21}^2 u_{11} -{\upbeta }_2 u_{11}^2 u_{21}\nonumber \\&\!\!\!\quad -\,\,{\upbeta }_3 u_{21}^3 -{\upbeta } _4 u_{11}^3 . \end{aligned}$$
(12)

The general solutions of Eqs. (7) and (8), can be written as

$$\begin{aligned} u_{11} =A_1 (T_1, T_2) \exp (i{\upomega }_{1 } T_0 )+\bar{{A}}_1 (T_1, T_2) \exp (-i{\upomega }_{1 } T_0),\nonumber \\ \end{aligned}$$
(13)
$$\begin{aligned} u_{21} =A_2 (T_1, T_2) \exp (i{\upomega }_{2 } T_0 )+\bar{{A}}_2 (T_1, T_2) \exp (-i{\upomega }_{2 } T_0),\nonumber \\ \end{aligned}$$
(14)

where \(\bar{{A}}_1, \bar{{A}}_2 \) are complex conjugates of \(A_1 , A_2 \), which are arbitrary complex functions of \(T_1 \) and \(T_2 \) at this level of approximation. It is determined by imposing the solvability conditions at the next levels of approximations. Substituting Eqs. (13) and (14) into Eqs. (9) and (10) and eliminating the secular terms, then the first-order approximations are given by

$$\begin{aligned} u_{12} (T_0, T_1, T_2)&= E_1 \exp (i{\upomega }_1 T_0)\nonumber \\&+\,\,E_2 \exp (i\Omega _3 T_0)\nonumber \\&+\,\,E_3 \exp (i(\Omega _1 \pm {\upomega }_1)T_0)\nonumber \\&+\,\,E_4\exp (i(\Omega _2 \pm {\upomega }_1)T_0)\nonumber \\&+\,\,E_5 \exp (i(\Omega _4 \pm {\upomega }_1)T_0)+cc, \end{aligned}$$
(15)
$$\begin{aligned} u_{22} (T_0, T_1, T_2)&= G_1 \exp (i{\upomega }_2 T_0) \nonumber \\&+\,\,G_2 \exp (i\Omega _3 T_0)\nonumber \\&+\,\,G_3 \exp (i(\Omega _1 \pm {\upomega }_2)T_0)\nonumber \\&+\,\,G_4 \exp (i(\Omega _2 \pm {\upomega }_2)T_0)\nonumber \\&+\,\,G_5 \exp (i(\Omega _4 \pm {\upomega }_2)T_0)+cc, \end{aligned}$$
(16)

where \(E_i, G_i (i=1, 2, \ldots ,5)\) are the complex functions in \(T_1 \)& \(T_2 \) and cc are the complex conjugates of the preceding terms. From Eqs. (13)–(16) into Eqs. (11) and (12) and eliminating the secular terms, the second-order approximations are given by

$$\begin{aligned} u_{13} (T_0, T_1, T_2)&= E_1 \exp (i{\upomega }_2 T_0)\nonumber \\&+\,\,E_2 \exp (i{\upomega }_3 T_0)+E_3 \exp (3i{\upomega }_1 T_0)\nonumber \\&+\,\,E_4 \exp (3i{\upomega }_2 T_0)+E_5 \exp (3i{\upomega }_3 T_0)\nonumber \\&+\,\,E_6 \exp (i({\upomega }_2 \pm 2{\upomega }_1)T_0)\nonumber \\&+\,\,E_7 \exp (i({\upomega }_3 \pm 2{\upomega }_1)T_0)\nonumber \\&+\,\,E_8 \exp (i(2{\upomega }_2 \pm {\upomega }_1)T_0)\nonumber \\&+\,\,E_9 \exp (i(2{\upomega }_3 \pm {\upomega }_1)T_0)\nonumber \\&+\,\,E_{10} \exp (i({\upomega }_2 \pm 2{\upomega }_3)T_0)\nonumber \\&+\,\,E_{11}\exp (i({\upomega }_3 \pm 2{\upomega }_2)T_0)\nonumber \\&+\,\,E_{12} \exp (i({\upomega }_3 \pm {\upomega }_2 \pm {\upomega } _1)T_0)\nonumber \\&+\,\,E_{13} \exp (i\Omega _3 T_0)\nonumber \\&+\,\,E_{14} \exp (i(\Omega _3 \pm \Omega _1)T_0)\nonumber \\&+\,\,E_{15} \exp (i(\Omega _3 \pm \Omega _2)T_0)\nonumber \\&+\,\,E_{16} \exp (i(\Omega _3 \pm \Omega _4)T_0)\nonumber \\&+\,\,E_{17} \exp (i(\Omega _1 \pm {\upomega }_1)T_0)\nonumber \\&+\,\,E_{18} \exp (i(\Omega _2 \pm {\upomega }_1)T_0)\nonumber \\&+\,\,E_{19} \exp (i(\Omega _4 \pm {\upomega }_1)T_0)\nonumber \\&+\,\,E_{20} \exp (i(2\Omega _1 \pm {\upomega }_1)T_0)\nonumber \\&+\,\,E_{21} \exp (i(2\Omega _2 \pm {\upomega }_1)T_0)\nonumber \\&+\,\,E_{22} \exp (i(2\Omega _4 \pm {\upomega }_1)T_0)\nonumber \\&+\,\,E_{23} \exp (i(\Omega _2 \pm {\upomega }_1 \pm {\upomega }_1)T_0)\nonumber \\&+\,\,E_{24} \exp (i(\Omega _4 \pm {\Omega }_1 \pm {\upomega }_1)T_0)\nonumber \\&+\,\,E_{25} \exp (i(\Omega _4 \pm {\Omega _2} \pm {\upomega }_1)T_0)+cc,\nonumber \\ \end{aligned}$$
(17)
$$\begin{aligned} u_{23} (T_0, T_1, T_2)&= G_1 \exp (i{\upomega }_1 T_0)+G_2 \exp (i{\upomega }_3 T_0)\nonumber \\&+\,\,G_3 \exp (3i{\upomega }_1 T_0)+G_4 \exp (3i{\upomega }_2 T_0)\nonumber \\&+\,\,G_5 \exp (3i{\upomega }_3 T_0)\nonumber \\&+\,\,G_6 \exp (i({\upomega }_2 \pm 2{\upomega }_1)T_0)\nonumber \\&+\,\,G_7 \exp (i(2{\upomega }_2 \pm {\upomega }_1)T_0)\nonumber \\&+\,\,G_8 \exp (i({\upomega }_3 \pm 2{\upomega }_1)T_0)\nonumber \\&+\,\,G_9 \exp (i(2{\upomega }_3 \pm {\upomega }_1)T_0)\nonumber \\&+\,\,G_{10} \exp (i({\upomega }_2 \pm 2{\upomega }_3)T_0)\nonumber \\&+\,\,G_{11} \exp (i(2{\upomega }_2 \pm {\upomega }_3)T_0)\nonumber \\&+\,\,G_{12} \exp (i({\upomega }_3 \pm {\upomega }_2 \pm {\upomega }_1)T_0)\nonumber \\&+\,\,G_{13} \exp (i\Omega _3 T_0)\nonumber \\&+\,\,G_{14} \exp (i(\Omega _3\pm \Omega _1)T_0)\nonumber \\&+\,\,G_{15} \exp (i(\Omega _3 \pm \Omega _2)T_0)\nonumber \\&+\,\,G_{16} \exp (i(\Omega _4 \pm \Omega _3)T_0)\nonumber \\&+\,\,G_{17} \exp (i(\Omega _1 \pm {\upomega }_2)T_0)\nonumber \\&+\,\,G_{18} \exp (i(\Omega _2 \pm {\upomega }_2)T_0)\nonumber \\&+\,\,G_{19}\exp (i(\Omega _4 \pm {\upomega }_2)T_0)\nonumber \\&+\,\,G_{20} \exp (i(2\Omega _1\pm {\upomega }_2)T_0)\nonumber \\&+\,\,G_{21} \exp (i(2\Omega _2 \pm {\upomega }_2)T_0)\nonumber \\&+\,\,G_{22} \exp (i(2\Omega _4 \pm {\upomega }_2)T_0)\nonumber \\&+\,\,G_{23} \exp (i(\Omega _2 \pm {\upomega }_1 \pm \upomega _2)T_0)\nonumber \\&+\,\,G_{24} \exp (i(\Omega _4 \pm \Omega _1 \pm {\upomega }_2)T_0)\nonumber \\&+\,\,G_{25} \exp (i(\Omega _4 \pm \Omega _2 \pm {\upomega }_2)T_0)+cc,\nonumber \\ \end{aligned}$$
(18)

where \(E_i, G_i (i=1, 2, \ldots ,25)\) are the complex functions in \(T_1 \) and \(T_2\). From the above-derived solutions, the reported resonance cases are

  • Primary resonance: \(\Omega _1 \cong {\upomega }_n, \Omega _2 \cong {\upomega }_n, \Omega _3 \cong {\upomega }_n, \Omega _4 \cong {\upomega }_n, n=1, 2\).

  • Sub-harmonic resonance: \(\Omega _1 \cong 2{\upomega }_n, \Omega _2 \cong 2{\upomega }_n, \Omega _4 \cong 2{\upomega }_n \).

  • Internal or secondary resonance: \({\upomega }_1 \cong {\upomega } _2, \upomega _1 \cong 3 {\upomega }_2, \upomega _2 \cong 3 {\upomega }_1 \).

  • Combined resonance: \(\Omega _3 \pm \Omega _t \cong {\upomega }_n,\Omega _4 \pm \Omega _m \cong 2{\upomega }_n,\Omega _2 \pm \Omega _1 \cong 2{\upomega }_n, t=1,2,4\) and \(m=1, 2\).

  • Simultaneous or incident resonance Any combination of the above resonance cases is considered as simultaneous resonance.

3.1 Simultaneous primary and internal resonance

For the simultaneous primary and internal resonance case \(\Omega _3 \cong {\upomega }_1, \upomega _1 \cong {\upomega }_2 \), we can introduce external and internal detuning parameters \({\upsigma }_1 \) and \({\upsigma } _2 \) such that:

$$\begin{aligned} \Omega _3 ={\upomega }_1 +{\upsigma }_1 ={\upomega }_1 +{\upvarepsilon } \hat{{{\upsigma } }}_1, \quad {\upomega }_2 ={\upomega }_1 +{\upsigma }_2 ={\upomega }_1 +{\upvarepsilon } \hat{{{\upsigma } }}_2 .\nonumber \\ \end{aligned}$$
(19)

Substituting Eq. (19) into Eqs. (9)–(12) and eliminating the secular terms leads to solvability conditions for the first and second-order expansions as:

$$\begin{aligned} 2i{\upomega }_1 D_1 A_1&= -i\hat{{{\upmu } }}_1 {\upomega }_1 A_1 +\frac{\hat{{f}}_1 }{2} \exp (i\hat{{{\upsigma } }}_{1 } T_1), \end{aligned}$$
(20)
$$\begin{aligned} 2i{\upomega }_2 D_1 A_2&= -i\hat{{{\upmu } }}_2 {\upomega }_2 A_2 +\frac{\hat{{f}}_2 }{2}\exp (i(\hat{{{\upsigma } }}_1 -\hat{{{\upsigma } }}_{2 })T_1), \end{aligned}$$
(21)
$$\begin{aligned} 2i{\upomega }_1 D_2 A_1&= \frac{\hat{{{\upmu } }}_1^2 }{4}A_1 +\frac{i\hat{{{\upmu } }}_{1 } \hat{{f}}_1 }{8{\upomega }_1 }\exp (i\hat{{{\upsigma } }}_{1 } T_1)\nonumber \\&-\,\,\frac{\hat{{{\upsigma } }}_{1 } \hat{{f}}_1 }{4{\upomega }_1 }\exp (i\hat{{{\upsigma } }}_{1 } T_1)\nonumber \\&-\,\,\left\{ {\frac{\hat{{f}}_{11}^2 }{2(\Omega _1^2 -4{\upomega }_1^2 )}+\frac{\hat{{f}}_{12}^2 }{2(\Omega _2^2 -4{\upomega }_1^2)}}\right. \nonumber \\&\left. +\,\,{\frac{\hat{{f}}_{14}^2 }{2(\Omega _4^2 -4{\upomega }_1^2)}}\right\} A_1\nonumber \\&-\,\,\left\{ {2{\upalpha }_1 A_1 \bar{{A}}_1 +3{\upalpha }_4 A_2 \bar{{A}}_2 }\right\} A_2 \exp (i\hat{{{\upsigma } }}_{2 } T_1)\nonumber \\&-\,\,{\upalpha }_1 A_1^2 \bar{{A}}_2 \exp (-i\hat{{{\upsigma } }}_{2} T_1)\nonumber \\&-\,\,\left\{ {2{\upalpha }_2 A_2 \bar{{A}}_2 +3{\upalpha }_3 A_1 \bar{{A}}_1 }\right\} A_1, \end{aligned}$$
(22)
$$\begin{aligned}&2i{\upomega }_2 D_2 A_2 =\frac{\hat{{{\upmu } }}_2^2 }{4}A_2 +\frac{i\hat{{{\upmu } }}_{2 } \hat{{f}}_2 }{8{\upomega }_2 }\exp (i(\hat{{{\upsigma } }}_{1 } -\hat{{{\upsigma } }}_2)T_1)\nonumber \\&\quad -\,\,\frac{\hat{{{\upsigma }}}_{2 } \hat{{f}}_2 }{4{\upomega }_2 }\exp (i(\hat{{{\upsigma } }}_{1 } -\hat{{{\upsigma }}}_2)T_1)-\left\{ {\frac{\hat{{f}}_{21}^2 }{2(\Omega _1^2 -4{\upomega }_2^2)}}\right. \nonumber \\&\quad \left. {+\,\,\frac{\hat{{f}}_{22}^2 }{2(\Omega _2^2 -4{\upomega }_2^2 )}+\frac{\hat{{f}}_{24}^2 }{2(\Omega _4^2 -4{\upomega }_2^2)}}\right\} A_2\nonumber \\&\quad -\,\,\left\{ {2{\upbeta }_1 A_2 \bar{{A}}_2 +3{\upbeta }_4 A_1 \bar{{A}}_1} \right\} A_1 \exp (-i\hat{{{\upsigma } }}_{2 } T_1)\nonumber \\&\quad -\,\,{\upbeta }_1 A_2^2 \bar{{A}}_1 \exp (i\hat{{{\upsigma } }}_{2 } T_1)-{\upbeta }_2 A_1^2 \bar{{A}}_2 \exp (-2i\hat{{{\upsigma } }}_{2 } T_1)\nonumber \\&\quad -\,\,\left\{ {2{\upbeta }_2 \bar{{A}}_1 A_1 +3{\upbeta }_3 A_2 \bar{{A}}_2 } \right\} A_2 . \end{aligned}$$
(23)

Letting \(A_n (T_1, T_2)=\frac{\hat{{a}}_n }{2} \exp (i{\upvarphi }_n) , a_n ={\upvarepsilon } \hat{{a}}_n, n=1, 2\) where \(a_{n}\) and \({\upvarphi }_n \) are real functions, and using \(\frac{dA_n }{d t}={\upvarepsilon } D_1 A_n +{\upvarepsilon }^{2} D_2 A_n \) and separating real and imaginary parts, we obtain the autonomous equation of the modulation of the amplitudes and phases of the response as follows:

$$\begin{aligned} \dot{a}_1&= -\frac{{\upmu }_1 }{2}a_1 -\frac{{\upalpha }_1 }{8{\upomega }_1 }a_1^2 a_2 \sin {\uptheta }_2-\frac{3{\upalpha }_4 }{8{\upomega }_1 }a_2^3 \sin {\uptheta }_2\nonumber \\&+\,\,\left\{ {\frac{f_1 }{2{\upomega }_1}-\frac{{\upsigma }_1 f_1 }{4{\upomega }_1^2 }}\right\} \sin {\uptheta }_1 +\frac{{\upmu }_1 f_1 }{8{\upomega }_1^2 }\cos {\uptheta }_1,\nonumber \\ \end{aligned}$$
(24)
$$\begin{aligned} a_1 \dot{{\upvarphi } }_1&= \left\{ {-\frac{{\upmu }_1^2 }{8{\upomega }_1 }+\frac{\Gamma _1 }{2{\upomega }_1 }}\right\} a_1 +\frac{3{\upalpha }_1 }{8{\upomega }_1 }a_1^2 a_2 \cos {\uptheta }_2\nonumber \\&+\,\,\frac{3{\upalpha }_4 }{8{\upomega }_1 }a_2^3 \cos {\uptheta }_2 +\frac{{\upalpha } _2 }{4{\upomega }_1 }a_1 a_2^2 +\frac{3{\upalpha }_3 }{8{\upomega }_1 }a_1^3\nonumber \\&-\,\,\left\{ {\frac{f_1 }{2{\upomega }_1 }-\frac{{\upsigma }_1 f_1 }{4{\upomega } _1^2 }}\right\} \cos {\uptheta }_1 +\frac{{\upmu }_1 f_1 }{8{\upomega }_1^2 }\sin {\uptheta }_1,\nonumber \\ \end{aligned}$$
(25)
$$\begin{aligned} \dot{a}_2&= -\frac{{\upmu }_2 }{2}a_2 +\frac{{\upbeta }_2 }{8{\upomega }_2 }a_1^2 a_2 \sin 2{\uptheta }_2\nonumber \\&+\,\,\frac{3{\upbeta }_4 }{8{\upomega } _2 }a_1^3 \sin {\uptheta }_2 +\frac{{\upbeta }_1 }{8{\upomega }_2 }a_2^2 a_1 \sin {\uptheta }_2 \nonumber \\&+\,\,\frac{{\upmu }_2 f_2 }{8{\upomega }_2^2 }\cos ({\uptheta }_1 -{\uptheta }_2)\nonumber \\&+\,\,\left\{ {\frac{f_2 }{2{\upomega }_2 }-\frac{({\upsigma }_1 -{\upsigma }_2) f_2 }{4{\upomega }_2^2 }}\right\} \sin ({\uptheta }_1 -{\uptheta } _2),\nonumber \\ \end{aligned}$$
(26)
$$\begin{aligned} a_2 \dot{{\upvarphi } }_2&= \left\{ {-\frac{{\upmu }_2^2 }{8{\upomega }_2 }+\frac{\Gamma _2 }{2{\upomega }_2 }}\right\} a_2 +\frac{{\upbeta }_2 }{8{\upomega }_2 }a_1^2 a_2 \cos 2{\uptheta }_2\nonumber \\&+\,\,\frac{{\upbeta }_2 }{4{\upomega }_2 }a_1^2 a_2 +\frac{3{\upbeta }_3 }{8{\upomega }_2 }a_2^3 +\frac{3{\upbeta }_4 }{8{\upomega }_2 }a_1^3 \cos {\uptheta }_2 \nonumber \\&+\,\,\frac{3{\upbeta }_1}{8{\upomega }_2 }a_2^2 a_1 \cos {\uptheta }_2\nonumber \\&+\,\,\left\{ {\frac{({\upsigma }_1-{\upsigma }_2) f_2 }{4{\upomega }_2^2 } -\frac{f_2 }{2{\upomega }_2 }}\right\} \cos ({\uptheta }_1 -{\uptheta }_2)\nonumber \\&+\,\,\frac{{\upmu }_2 f_2 }{8{\upomega }_2^2 }\sin ({\uptheta }_1 -{\uptheta }_2),\nonumber \\ \end{aligned}$$
(27)

where \(\Gamma _n =\left\{ {\frac{f_{n1}^2 }{2(\Omega _1^2 -4{\upomega } _n^2)}+\frac{f_{n2}^2 }{2(\Omega _2^2 -4{\upomega }_n^2 )}+\frac{f_{n4}^2 }{2(\Omega _4^2 -4{\upomega }_n^2)}}\right\} , n=1,2, {\uptheta }_1 =\hat{{{\upsigma } }}_1 T_1 -{\upvarphi }_1 \) and \({\uptheta }_2 =\hat{{{\upsigma } }}_2 T_1 +{\upvarphi }_2 -{\upvarphi }_1 \).

Steady-state solutions of the system correspond to the fixed points of Eqs. (24)–(27), which in turn correspond to

$$\begin{aligned} \dot{{\upvarphi } }_1 ={\upsigma }_1\hbox { and } \dot{{\upvarphi } }_2 ={\upsigma }_1 -{\upsigma }_2 . \end{aligned}$$
(28)

Hence, the fixed points of Eqs. (24)–(27) are given by

$$\begin{aligned}&\!\!\!-\frac{{\upmu }_1 }{2}a_1 -\frac{{\upalpha }_1 }{8{\upomega }_1 }a_1^2 a_2 \sin {\uptheta }_2 -\frac{3{\upalpha }_4 }{8{\upomega }_1 }a_2^3 \sin {\uptheta }_2\nonumber \\&\!\!\!\quad +\left\{ {\frac{f_1 }{2{\upomega }_1 }-\frac{{\upsigma }_1 f_1 }{4{\upomega }_1^2 }}\right\} \sin {\uptheta }_1 +\frac{{\upmu }_1 f_1 }{8{\upomega }_1^2 }\cos {\uptheta }_1 =0, \end{aligned}$$
(29)
$$\begin{aligned}&\!\!\!a_1 {\upsigma }_1 +\left\{ {\frac{{\upmu }_1^2 }{8{\upomega }_1} -\frac{\Gamma _1 }{2{\upomega }_1 }}\right\} a_1 -\frac{3{\upalpha }_1}{8{\upomega }_1 }a_1^2 a_2 \cos {\uptheta }_2\nonumber \\&\!\!\!\quad -\,\,\frac{{\upalpha }_2 }{4{\upomega }_1}a_1 a_2^2 -\frac{3{\upalpha }_3 }{8{\upomega }_1 }a_1^3 -\frac{3{\upalpha }_4}{8{\upomega }_1 }a_2^3 \cos {\uptheta }_2 -\frac{{\upmu }_1 f_1 }{8{\upomega }_1^2}\sin {\uptheta }_1\nonumber \\&\!\!\!\quad +\,\,\left\{ {\frac{f_1 }{2{\upomega }_1 }-\frac{{\upsigma }_1 f_1 }{4{\upomega }_1^2 }}\right\} \cos {\uptheta }_1 =0, \end{aligned}$$
(30)
$$\begin{aligned}&\!\!\!-\frac{{\upmu }_2 }{2}a_2 +\frac{{\upbeta }_1 }{8{\upomega }_2} a_2^2 a_1 \sin {\uptheta }_2 +\frac{{\upbeta }_2 }{8{\upomega }_2 }a_1^2 a_2 \sin 2{\uptheta }_2\nonumber \\&\!\!\!\quad +\,\,\frac{3{\upbeta }_4 }{8{\upomega }_2 }a_1^3 \sin {\uptheta }_2 +\left\{ {\frac{f_2 }{2{\upomega }_2 }-\frac{({\upsigma }_1 -{\upsigma }_2) f_2 }{4{\upomega }_2^2 }}\right\} \sin ({\uptheta }_1 -{\uptheta }_2)\nonumber \\&\!\!\!\quad +\frac{{\upmu }_2 f_2 }{8{\upomega }_2^2 }\cos ({\uptheta }_1 -{\uptheta }_2)=0, \end{aligned}$$
(31)
$$\begin{aligned}&\!\!\!a_2 ({\upsigma }_2 -{\upsigma }_1)-\left\{ {\frac{{\upmu }_2^2 }{8{\upomega }_2 }-\frac{\Gamma _2 }{2{\upomega }_2 }}\right\} a_2 +\frac{3{\upbeta }_1 }{8{\upomega }_2 }a_2^2 a_1 \cos {\uptheta }_2\nonumber \\&\!\!\!\quad +\,\frac{{\upbeta }_2}{8{\upomega }_2 }a_1^2 a_2 \cos 2{\uptheta }_2 +\frac{{\upbeta }_2 }{4{\upomega }_2 }a_1^2 a_2 +\frac{3{\upbeta }_3 }{8{\upomega }_2 }a_2^3 +\frac{3{\upbeta }_4}{8{\upomega }_2 }a_1^3 \cos {\uptheta }_2\nonumber \\&\!\!\!\quad +\,\left\{ {\frac{({\upsigma }_1-{\upsigma }_2) f_2 }{4{\upomega }_2^2 } -\frac{f_2 }{2{\upomega }_2 }}\right\} \cos ({\uptheta }_1 -{\uptheta }_2)\nonumber \\&\!\!\!\quad +\,\frac{{\upmu }_2 f_2 }{8{\upomega }_2^2 }\sin ({\uptheta }_1 -{\uptheta }_2)=0. \end{aligned}$$
(32)

There are three possibilities besides the trivial solution

  1. (1)

    \(a_1 \ne 0, a_2 =0\) (Single mode)

  2. (2)

    \(a_2 \ne 0, a_1 =0\) (Single mode)

  3. (3)

    \(a_1 \ne 0, a_2 \ne 0\) (Two modes)

  • Case (1): In this case, where \(a_2 =0\), the frequency response equation is given by

    $$\begin{aligned}&\frac{9{\upalpha }_3^2 }{64{\upomega }_1^2 }a_1^6 +\left[ {R_3 +\frac{3{\upalpha }_3 {\upsigma }_1 }{4{\upomega }_1 }}\right] a_1^4\nonumber \\&+\left[ {R_2 +{\upsigma }_1^2 +\frac{{\upmu }_1^2 {\upsigma }_1 }{4{\upomega }_1} -\frac{\Gamma _1 {\upsigma }_1 }{{\upomega }_1 }}\right] a_1^2 -\frac{{\upmu } _1^2 f_1^2 }{64{\upomega }_1^4 }-R_1^2 =0.\nonumber \\ \end{aligned}$$
    (33)

    This is a single-mode solution.

  • Case (2): In this case, where \(a_1 =0\), the frequency response equation is given by

    $$\begin{aligned}&\!\!\!\frac{9{\upbeta }_3^2 }{64{\upomega }_2^2 }a_2^6 +\left[ {Q_3 +\frac{3{\upbeta } _3 ({\upsigma }_2 -{\upsigma }_1)}{4{\upomega }_2 }}\right] a_2^4 \nonumber \\&{+}\left[ {Q_2+({\upsigma }_2 -{\upsigma }_1)^{2}} {-\frac{{\upmu }_2^2 ({\upsigma } _2 -{\upsigma }_1)}{4{\upomega }_2 }{+}\frac{\Gamma _2 ({\upsigma }_2 -{\upsigma }_1 )}{{\upomega }_2 }}\right] a_2^2\nonumber \\&-\,\frac{{\upmu }_2^2 f_2^2 }{64{\upomega }_2^4 }-Q_1^2 =0. \end{aligned}$$
    (34)

    This is a single-mode solution.

  • Case (3): In this case, where \(a_1 \ne 0, a_2 \ne 0\), this is the practical case, the frequency response equations are given by

    $$\begin{aligned}&\!\!\!\frac{9{\upalpha }_3^2 }{64{\upomega }_1^2 }a_1^6 +\left[ {R_3+\frac{3{\upalpha }_3 {\upsigma }_1 }{4{\upomega }_1 }}\right] a_1^4\nonumber \\&\!\!\!\!\quad +\,\,\left[ {R_2 +{\upsigma }_1^2 +\frac{{\upmu }_1^2 {\upsigma }_1 }{4{\upomega }_1} -\frac{\Gamma _1 {\upsigma }_1 }{{\upomega }_1 }}\right] a_1^2\nonumber \\&\!\!\!\!\quad -\,\,\frac{{\upmu }_1^2 f_1^2 }{64{\upomega }_1^4 }-R_1^2 +\frac{3R_1 {\upalpha }_4 }{4{\upomega }_1 }a_2^3 +\frac{3R_1 {\upalpha }_1 }{4{\upomega }_1 }a_1^2 a_2\nonumber \\&\!\!\!\!\quad -\frac{9{\upalpha }_1^2 }{64{\upomega }_1^2 }a_1^4 a_2^2 -\frac{9{\upalpha }_1{\upalpha }_4 }{32{\upomega }_1^2 }a_1^2 a_2^4 -\frac{9{\upalpha }_4^2}{64{\upomega }_1^2 }a_2^6 =0, \end{aligned}$$
    (35)
    $$\begin{aligned}&\!\!\!\frac{9{\upbeta }_3^2 }{64{\upomega }_2^2 }a_2^6 +\left[ {Q_3 +\frac{3{\upbeta } _3 ({\upsigma }_2 -{\upsigma }_1)}{4{\upomega }_2 }}\right] a_2^4 \left[ {Q_2+({\upsigma }_2 -{\upsigma }_1)^{2}}\right. \nonumber \\&\!\!\!\!\quad \left. +\,\,-\frac{{\upmu }_2^2 ({\upsigma } _2 -{\upsigma }_1)}{4{\upomega }_2 }+\frac{\Gamma _2 ({\upsigma }_2 -{\upsigma }_1 )}{{\upomega }_2 }\right] a_2^2\nonumber \\&\!\!\!\!\quad -\,\,\frac{{\upmu }_2^2 f_2^2 }{64{\upomega }_2^4 } -Q_1^2 +\frac{3Q_1 {\upbeta }_1 }{4{\upomega }_2 }a_2^2 a_1 +\frac{3Q_1 {\upbeta }_4 }{4{\upomega }_2 }a_1^3\nonumber \\&\!\!\!\!\quad +\,\,\frac{Q_1 {\upbeta }_2 }{4{\upomega }_2 }a_1^2 a_2 -\frac{3{\upbeta }_2 \beta _4 }{32{\upomega }_2^2 }a_1^5 a_2\nonumber \\&\!\!\!\!\quad \,\,-\frac{9{\upbeta }_1^2 }{64{\upomega }_2^2 }a_2^4 a_1^2 -Q_4 a_1^4 a_2^2 -\frac{9{\upbeta }_4^2 }{64{\upomega }_2^2 }a_1^6\nonumber \\&\!\!\!\!\quad -\,\,\frac{3{\upbeta }_2 \beta _1 }{32{\upomega }_2^2 }a_1^3 a_2^3 =0, \end{aligned}$$
    (36)

    which is a two-mode solution. where

    $$\begin{aligned}&R_1 =\left[ {\frac{1}{2{\upomega }_1 }-\frac{{\upsigma }_1 }{4{\upomega } _1^2 }}\right] f_1 ,\\&R_2 =\left[ {\frac{{\upmu }_1^2 }{4}+\frac{{\upmu } _1^4 }{64{\upomega }_1^2 }+\frac{\Gamma _1^2 }{4{\upomega }_1^2 }-\frac{\Gamma _1 {\upmu }_1^2 }{8{\upomega }_1^2 }}\right] ,\\&R_3 =3\left[ {\frac{{\upmu }_1^2 }{32{\upomega }_1^2 }-\frac{\Gamma _1 }{8{\upomega }_1^2 }} \right] {\upalpha }_3,\\&Q_1 =\left[ {\frac{1}{2{\upomega }_2 }-\frac{({\upsigma }_1 -{\upsigma }_2)}{4{\upomega }_2^2 }}\right] f_2 ,\\&Q_2=\left[ {\frac{{\upmu }_2^2 }{4}+\frac{{\upmu }_2^4 }{64{\upomega }_2^2 }+\frac{\Gamma _2^2 }{4{\upomega }_2^2 }-\frac{\Gamma _2 {\upmu }_2^2 }{8{\upomega }_2^2 }}\right] ,\\&Q_3 =3\left[ {\frac{\Gamma _2 }{8{\upomega } _2^2 }-\frac{{\upmu }_2^2 }{32{\upomega }_2^2 }}\right] {\upbeta }_3 , Q_4 =\left[ {\frac{{\upbeta }_2^2 }{64{\upomega }_2^2 }+\frac{9{\upbeta }_1 \beta _4 }{32{\upomega }_2^2 }}\right] . \end{aligned}$$

4 Stability analysis

Here we study the problem of stability in two cases: linear and non-linear solutions.

4.1 Stability of linear solution

To study the stability of the linear solution, one investigates the solution of the linearized form of Eqs. (20)–(23) as

$$\begin{aligned} 2i{\upomega }_1 D_1 A_1&= -i\hat{{{\upmu } }}_1 {\upomega }_1 A_1 +\frac{\hat{{f}}_1 }{2} \exp (i\hat{{{\upsigma } }}_{1 } T_1), \end{aligned}$$
(37)
$$\begin{aligned} 2i{\upomega }_2 D_1 A_2&= -i\hat{{{\upmu } }}_2 {\upomega }_2 A_2 +\frac{\hat{{f}}_2 }{2}\exp (i(\hat{{{\upsigma } }}_1 -\hat{{{\upsigma } }}_{2 })T_1), \end{aligned}$$
(38)
$$\begin{aligned} 2i{\upomega }_1 D_2 A_1&= \frac{\hat{{{\upmu } }}_1^2 }{4}A_1 +\frac{i\hat{{{\upmu } }}_{1 } \hat{{f}}_1 }{8{\upomega }_1 }\exp (i\hat{{{\upsigma } }}_{1 } T_1)\nonumber \\&-\frac{\hat{{{\upsigma } }}_{1 } \hat{{f}}_1 }{4{\upomega }_1 }\exp (i\hat{{{\upsigma } }}_{1 } T_1)-\Gamma _{1 } A_1, \end{aligned}$$
(39)
$$\begin{aligned} 2i{\upomega }_2 D_2 A_2&= \frac{\hat{{{\upmu } }}_2^2 }{4}A_2 +\frac{i\hat{{{\upmu } }}_{2 } \hat{{f}}_2 }{8{\upomega }_2 }\exp (i(\hat{{{\upsigma } }}_{1 } -\hat{{{\upsigma } }}_2)T_1)\nonumber \\&-\frac{\hat{{{\upsigma }}}_{2 } \hat{{f}}_2 }{4{\upomega }_2 }\exp (i(\hat{{{\upsigma } }}_{1 } -\hat{{{\upsigma } }}_2)T_1)-\Gamma _{2 } A_2, \end{aligned}$$
(40)

we express \(A_n\) in the form

$$\begin{aligned}&A_n =\frac{1}{2}(\hat{{p}}_n -i\hat{{q}}_n)\exp (iv_{n } T_1) \quad p_n ={\upvarepsilon } \hat{{p}}_n, q_n\nonumber \\&\quad ={\upvarepsilon } \hat{{q}}_n\,\quad n=1,2, \end{aligned}$$
(41)

where \(v_1 ={\upsigma }_1, v_2 ={\upsigma }_1 -{\upsigma }_2 \). Separating real and imaginary parts into expression, \(\frac{dA_n }{d t}={\upvarepsilon } D_1 A_n +{\upvarepsilon }^{2} D_2 A_n \) we obtain the autonomous equation of the modulation of the amplitudes and phases of the response

$$\begin{aligned} \dot{p}_1&= -\left( {\frac{{\upmu }_1 }{2}}\right) p_1 -\left( {\frac{{\upmu }_1^2 }{8{\upomega }_1 }+{\upsigma }_1 -\frac{\Gamma _1}{2{\upomega }_1 }}\right) q_1 +\frac{{\upmu }_{1 } f_1 }{8{\upomega }_1^2 },\nonumber \\ \end{aligned}$$
(42)
$$\begin{aligned} \dot{q}_1&= \left( {\frac{{\upmu }_1^2 }{8{\upomega }_1 }+{\upsigma }_1 -\frac{\Gamma _1 }{2{\upomega }_1 }}\right) p_1 -\left( {\frac{{\upmu }_1 }{2}}\right) q_1 -\frac{{\upsigma }_{1 } f_1 }{4{\upomega } _1^2 }, \end{aligned}$$
(43)
$$\begin{aligned} \dot{p}_2&= \left( {\frac{{\upmu }_2 }{2}}\right) p_2 -\left( {\frac{\Gamma _2 }{2{\upomega }_2 }+{\upsigma }_2 -{\upsigma }_1 -\frac{{\upmu }_2^2 }{8{\upomega }_2 }}\right) q_2 +\frac{{\upmu }_{2 } f_2}{8{\upomega }_2^2 },\nonumber \\ \end{aligned}$$
(44)
$$\begin{aligned} \dot{q}_2&= -\left( {\frac{\Gamma _2 }{2{\upomega }_2 }+{\upsigma }_2 -{\upsigma }_1 -\frac{{\upmu }_2^2 }{8{\upomega }_2 }}\right) p_2 +\left( {\frac{{\upmu }_2 }{2}}\right) q_2\nonumber \\&\quad +\,\frac{f_2 }{2{\upomega }_2 }-\frac{({\upsigma }_1 -{\upsigma }_2)f_2 }{4{\upomega }_2^2 }\quad . \end{aligned}$$
(45)

The stability of a particular equilibrium solution is ascertained by investigating the eigenvalues of the Jacobian matrix of the right-hand sides of Eqs. (42)–(45). The stable (unstable) solutions have been represented by solid (dotted) lines on the \({\upsigma }_1 \) and \({\upsigma }_2 \)-axis.

4.2 Stability of non-linear solution

To analyze the stability of the fixed points by Liapunov’s first method, one lets

$$\begin{aligned} a_n =a_{n0} +a_{n1}\quad \hbox { and }\quad {\uptheta }_n ={\uptheta }_{n0} +{\uptheta }_{n1} \quad (n = 1, 2), \end{aligned}$$
(46)

where \(a_{n0}\) and \({\uptheta }_{n0}\) are the solutions of Eqs. (29)–(32). Inserting Eq. (46) into Eqs. (24)–(27), and keeping only the linear terms in \(a_{n1}, {\uptheta }_{n1} \) we obtain:

$$\begin{aligned} \dot{a}_{11}&= \left\{ {-\frac{{\upmu }_1 }{2}-\frac{{\upalpha }_1 a_{10} a_{20} }{4{\upomega }_1 }\sin {\uptheta }_{20} }\right\} a_{11}\nonumber \\&+\,\,\left\{ {\left( {\frac{f_1 }{2{\upomega }_1 }-\frac{{\upsigma }_{1 } f_1 }{4{\upomega } _1^2 }}\right) \cos {\uptheta }_{10} -\frac{{\upmu }_{1 } f_1 }{8{\upomega }_1^2 }\sin {\uptheta }_{10} }\right\} {\uptheta }_{11}\nonumber \\&\left. {-\,\,\left\{ {\left( {\frac{{\upalpha }_1 a_{10}^2 }{8{\upomega }_1 }+\frac{9{\upalpha }_4 a_{20}^2 }{8{\upomega }_1 }}\right) \sin {\uptheta }_{20} }\right. }\right\} a_{21}\nonumber \\&-\,\,\left\{ {\left( {\frac{3{\upalpha }_4 a_{20}^3 }{8{\upomega }_1 }+\frac{{\upalpha }_1 a_{10}^2 a_{20} }{8{\upomega }_1 }}\right) \cos {\uptheta }_{20} }\right\} {\uptheta } _{21}, \end{aligned}$$
(47)
$$\begin{aligned} \dot{{\uptheta } }_{11}&= \left\{ \frac{{\upsigma }_1 }{a_{10} }+\frac{{\upmu } _1^2 }{8{\upomega }_1 a_{10} }-\frac{\Gamma _1 }{2{\upomega }_1 a_{10} }-\frac{3{\upalpha }_{1 } a_{20} }{4{\upomega }_1 }\cos {\uptheta }_{20}\right. \nonumber \\&\left. -\,\,\frac{{\upalpha }_{2 } a_{20}^2 }{4{\upomega }_1 a_{10} }-\frac{9{\upalpha }_{3 } a_{10} }{8{\upomega }_1 }\right\} a_{11}\nonumber \\&{+}\left\{ {\left( {\frac{{\upsigma }_{1 } f_1 }{4{\upomega }_1^2 } {-}\frac{f_1 }{2{\upomega }_1 }}\right) \frac{1}{a_{10} }\sin {\uptheta }_{10}}\right. \left. {{-}\frac{{\upmu }_1 f_1 }{8{\upomega }_1^2 a_{10} }\cos {\uptheta }_{10} } \right\} {\uptheta }_{11}\nonumber \\&-\,\,\left\{ {\frac{3{\upalpha }_1 {a}_{10} }{8{\upomega }_1 }\cos {\uptheta }_{20} +\frac{9{\upalpha }_4 a_{20}^3 }{8{\upomega }_1 a_{10} }\cos {\uptheta }_{20} +\frac{{\upalpha }_2 a_{20} }{2{\upomega }_1 }} \right\} a_{21}\nonumber \\&+\,\,\left\{ {\frac{3{\upalpha }_1 a_{10} {a}_{20} }{8{\upomega }_1 }\sin {\uptheta }_{20} +\frac{3{\upalpha }_4 a_{20}^3 }{8{\upomega }_1 a_{10} }\sin {\uptheta }_{20} }\right\} {\uptheta }_{21}, \end{aligned}$$
(48)
$$\begin{aligned} \dot{a}_{21}&= \left\{ {\frac{\left( {{\upbeta }_1 a_{20}^2 {+}9{\upbeta }_4 a_{10}^2 }\right) }{8{\upomega }_2 }\sin {\uptheta }_{20} {+}\frac{{\upbeta }_2 a_{10} a_{20} }{4{\upomega }_2 }\sin 2{\uptheta }_{20} }\right\} a_{11}\nonumber \\&+\,\,\left\{ {\left( {\frac{f_2 }{2{\upomega }_2 }-\frac{({\upsigma }_{1 } -{\upsigma }_2)f_2 }{4{\upomega }_2^2 }}\right) \cos ({\uptheta }_{10} -{\uptheta } _{20})}\right. \nonumber \\&\left. {-\,\,\frac{{\upmu }_{2 } f_2 }{8{\upomega }_2^2 }\sin ({\uptheta }_{10} -{\uptheta }_{20})}\right\} {\uptheta }_{11}\nonumber \\&{+}\left\{ {-\frac{{\upmu }_2 }{2}{+}\frac{{\upbeta }_1 a_{10} a_{20} }{4{\upomega }_2 }\sin {\uptheta }_{20} {+}\frac{{\upbeta }_2 a_{10}^2 }{8{\upomega }_2 }\sin 2{\uptheta }_{20} } \right\} a_{21}\nonumber \\&+\,\,\left\{ -\left( {\frac{f_2 }{2{\upomega }_2 }-\frac{({\upsigma }_1 -{\upsigma } _2)f_2 }{4{\upomega }_2^2 }}\right) \cos ({\uptheta }_{10} -{\uptheta }_{20})\right. \nonumber \\&\left. +\,\,\frac{{\upmu }_{2 } f_2 }{8{\upomega }_2^2 }\sin ({\uptheta }_{10} -{\uptheta } _{20})+\frac{{\upbeta }_2 a_{20} a_{10}^2 }{4{\upomega }_2 }\cos 2{\uptheta }_{20}\right. \nonumber \\&\left. {+\,\,\frac{\left( {{\upbeta }_1 a_{10} a_{20}^2 +3{\upbeta } _4 a_{10}^3 }\right) }{8{\upomega }_2 }\cos {\uptheta }_{20} }\right\} {\uptheta }_{21}, \end{aligned}$$
(49)
$$\begin{aligned} \dot{{\uptheta } }_{21}&= \left\{ \frac{{\upsigma }_1 }{a_{10} }+\frac{{\upmu } _1^2 }{8{\upomega }_1 a_{10} }-\frac{\Gamma _1 }{2{\upomega }_1 a_{10} }-\frac{3{\upalpha }_1 a_{20} }{4{\upomega }_1 }\cos {\uptheta }_{20}\right. \nonumber \\&\left. -\,\,\frac{{\upalpha }_2 a_{20}^2 }{4{\upomega }_1 a_{10} }-\frac{9{\upalpha }_3 a_{10} }{8{\upomega }_1 }+\frac{{\upbeta }_2 a_{10} }{2{\upomega }_2 }+\frac{3{\upbeta }_1 a_{20} }{8{\upomega }_2 }\cos {\uptheta }_{20}\right. \nonumber \\&\left. {+\,\,\frac{9{\upbeta }_4 a_{10}^2 }{8{\upomega }_2 a_{20} }\cos {\uptheta }_{20} +\frac{{\upbeta }_2 a_{10} }{4{\upomega }_2 }\cos 2{\uptheta }_{20} }\right\} a_{11}\nonumber \nonumber \\&+\,\,\left\{ \left( {\frac{{\upsigma }_1 f_1 }{4{\upomega } _1^2 }-\frac{f_1 }{2{\upomega }_1 }}\right) \frac{1}{a_{10} }\sin {\uptheta } _{10} -\frac{{\upmu }_1 f_1 }{8{\upomega }_1^2 a_{10} }\cos {\uptheta } _{10}\right. \\&+\,\,\frac{{\upmu }_2 f_2 }{8{\upomega }_2^2 a_{20} }\cos ({\uptheta }_{10} -{\uptheta }_{20})-\left( \frac{({\upsigma }_1 -{\upsigma }_2)f_2 }{4{\upomega }_2^2 }-\frac{f_2 }{2{\upomega }_2 }\right) \nonumber \nonumber \\&\times \left. \frac{1}{a_{20} }\sin ({\uptheta }_{10} -{\uptheta }_{20})\right\} {\uptheta }_{11}\nonumber \\&+\,\,\left\{ {-\frac{3{\upalpha }_1 a_{10} }{8{\upomega }_1 }\cos {\uptheta }_{20} }\right. -\frac{9{\upalpha }_4 a_{20}^3 }{8{\upomega }_1 a_{10} }\cos {\uptheta }_{20} -\frac{{\upalpha }_2 a_{20} }{2{\upomega }_1 }\nonumber \nonumber \\&+\,\,\frac{({\upsigma }_2 -{\upsigma }_1)}{a_{20} } -\frac{{\upmu }_2^2 }{8{\upomega }_2 a_{20} }+\frac{\Gamma _2}{2{\upomega }_2 a_{20} } +\frac{3{\upbeta }_1 a_{10} }{4{\upomega }_2 }\cos {\uptheta }_{20}\nonumber \\&\left. {+\,\,\frac{{\upbeta }_2 a_{10}^2 }{8{\upomega }_2 a_{20} }\cos 2{\uptheta } _{20} +\frac{{\upbeta }_2 a_{10}^2 }{4{\upomega }_2 a_{20} }+\frac{9{\upbeta }_3 a_{20} }{8{\upomega }_2 }}\right\} a_{21}\nonumber \nonumber \\&+\,\,\left\{ {\frac{3{\upalpha }_1 a_{10} a_{20} }{8{\upomega }_1 }\sin {\uptheta }_{20} +\frac{3{\upalpha }_4 a_{20}^3 }{8{\upomega }_1 a_{10} }\sin {\uptheta }_{20} }\right. \nonumber \\&+\,\,\left( {\frac{({\upsigma }_1 -{\upsigma }_2)f_2 }{4{\upomega }_2^2 }-\frac{f_2 }{2{\upomega }_2 }}\right) \frac{1}{a_{20} }\sin ({\uptheta }_{10} -{\uptheta } _{20})\nonumber \\&-\,\,\frac{{\upmu }_2 f_2 }{8{\upomega }_2^2 a_{20} }\cos ({\uptheta }_{10} -{\uptheta }_{20})-\frac{3{\upbeta }_1 a_{10} a_{20} }{8{\upomega }_2 }\sin {\uptheta }_{20}\nonumber \\&\left. {-\,\,\frac{{\upbeta }_2 a_{10}^2 }{4{\upomega }_2 }\sin 2{\uptheta }_{20} -\frac{3{\upbeta }_4 a_{10}^3 }{8{\upomega }_2 a_{20} }\sin {\uptheta }_{20} }\right\} {\uptheta }_{21}, \end{aligned}$$
(50)

To study the stability of the fixed points corresponding to the practical case, we let \(a_{ n1} \ne 0\) and \({\uptheta }_{n1} \ne 0\) in Eqs. (47)–(50), and obtain the eigenvalues from the Jacobian matrix of the right hand sides. The zeros of the characteristic equation are given by

$$\begin{aligned} {\uplambda }^{4}+L_1 {\uplambda }^{3}+L_2 {\uplambda }^{2}+L_3 {\uplambda } +L_4 =0, \end{aligned}$$
(51)

where \(L_1,L_2,L_3 \) and \(L_4 \) are functions of the parameters \(( {\upomega }_1, \upomega _2,{\upmu }_1,{\upmu }_2, {\upalpha }_1 , {\upalpha }_2,{\upalpha }_3, {\upalpha }_4, {\upbeta }_1, \beta _2, {\upbeta }_3 ,\beta _4,f_1,f_2, {\uptheta }_1,\) \( {\uptheta }_2, {\upsigma }_1, {\upsigma }_2 )\). According to Routh–Huriwitz criterion, the necessary and sufficient conditions for all roots of Eq. (51) to possess negative real parts is that

$$\begin{aligned}&\!\!\!L_{1 } > 0, L_{1 }L_{2}-L_{3}>0, L_{3}(L_{1}L_{2}-L_{3})\nonumber \\&\quad -L_{1}^{2}L_{4}> 0, L_{4}> 0. \end{aligned}$$
(52)

In all frequency response curves, solid lines comprise the stable solutions whereas dotted lines stand for unstable solutions.

5 Numerical results

When the amplitude achieves a constant nontrivial value, a steady state vibration exists. Using the frequency response equations, we can assess the influence of the damping coefficients, the nonlinear parameters and the excitation amplitude on the steady state amplitudes. The frequency response Eqs. (33)–(36) are nonlinear equations in \(a_1, a_2 \) which are solved numerically. The numerical results are shown in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20 and 21. In all figures the region of stability of the nonlinear solutions is determined by applying the Routh-Hurwitz criterion. The non-linear solution has stable and unstable solutions which are represented on the frequency response curves by solid and dotted lines and also the linear solution has stable and unstable solutions which are represented by solid and dotted lines on the \({\upsigma }_1 \) and \({\upsigma }_2 \) -axis. From the geometry of the figures, we observe that the each curve are continuous and have stable and unstable solution.

Fig. 2
figure 2

Comparison between analytical prediction using multiple time scale and numerical integration of the first mode

Full size image
Fig. 3
figure 3

Effects of the nonlinear parameter \({\upalpha }_3 \)

Full size image
Fig. 4
figure 4

Effects of the external excitation \(f_1\)

Full size image
Fig. 5
figure 5

Effects of the linear damping \({\upmu }_1 \)

Full size image
Fig. 6
figure 6

Effects of the natural frequency \({\upomega }_1 \)

Full size image
Fig. 7
figure 7

Comparison between analytical prediction using multiple time scale and numerical integration of the second mode

Full size image
Fig. 8
figure 8

Effects of the nonlinear parameter \({\upbeta }_4 \)

Full size image
Fig. 9
figure 9

Effects of the external excitation \(f_2\)

Full size image
Fig. 10
figure 10

Effects of the linear damping \({\upmu }_2\)

Full size image
Fig. 11
figure 11

Effects of the natural frequency \({\upomega }_2 \)

Full size image
Fig. 12
figure 12

Effects of the detuning parameter \({\upsigma }_2 \)

Full size image
Fig. 13
figure 13

Effects of the external excitation \(f_1 \)

Full size image
Fig. 14
figure 14

Effects of the external excitation \(f_2 \)

Full size image
Fig. 15
figure 15

Effects of the nonlinear parameter \({\upalpha }_1 \)

Full size image
Fig. 16
figure 16

Effects of the nonlinear parameter \({\upbeta }_1 \)

Full size image
Fig. 17
figure 17

Effects of the natural frequencies

Full size image
Fig. 18
figure 18

Effects of the detuning parameter \({\upsigma }_1 \)

Full size image
Fig. 19
figure 19

Effects of the nonlinear parameter \({\upalpha }_2 \)

Full size image
Fig. 20
figure 20

Effects of the nonlinear parameter \({\upalpha }_3 \)

Full size image
Fig. 21
figure 21

Effects of the nonlinear parameter \({\upalpha }_4 \)

Full size image

5.1 Amplitude frequency responses

To check the accuracy of the analytical solution derived by the multiple time scale in predicting the amplitude of the first mode, we compare the amplitude of the first mode obtained from frequency response equation with values obtained from numerical integration of Eq. (1). Figure 2 shows a comparison of these outputs for the first mode. The effects of the detuning parameter \({\upsigma }_1 \) on the steady state amplitude of the first mode for the stability first case, where \(a_1 \ne 0, a_2 =0\), for the parameters: \({\upalpha }_3 =0.02,f_1 =2,{\upmu }_1 =0.2, f_{11} =0.1,f_{12} =0.2, \quad f_{14} =0.3, \Omega _1 =1, \Omega _2 =1.2, \Omega _4 =1.4, {\upomega }_1 =2.3\) is shown in Fig. 2. Figures 3, 4, 5 and 6, show the effects of the non-linear spring stiffness \({\upalpha }_{3}\), the external excitation amplitude \(f_{1} \), the damping coefficient \({\upmu }_1 \), the first mode natural frequency \({\upomega }_1 \) for the system. Figure 3 shows that as the non-linear spring stiffness \({\upalpha }_{3}\) is increased the continuous curve is moved downwards. Also, the negative and positive values of \({\upalpha }_{3}\), produce either hard or soft spring respectively as the curve is either bent to the right or to the left, leading to the appearance of the jump phenomenon. The region of stability is increased for increasing value of \({\upalpha }_{3}\). It is clear from Fig. 4 that the steady state amplitude \(a_1 \) is increasing for increasing value of external excitation force \(f_1 \), the curve bends more to the left, and hence the softening behavior becomes stronger and the zone of instability is increased. Figures 5 and 6 shows that the steady state amplitude \(a_1 \) is inversely proportional to \({\upmu }_1 \) and \({\upomega }_1 \) also for decreasing \({\upmu }_1 \) or \({\upomega }_1 \) the curve is bending to the left.

Figures 7, 8, 9, 10 and 11, show the effects of system parameters on the amplitude frequency response curves for the stability of the second case, where \(a_1 =0, a_2 \ne 0 \). Figure 7 shows a comparison between analytical prediction using multiple time scale and numerical integration of the second mode. A comparison between the solutions obtained numerically with that prediction from the multiple time scale show an excellent agreement in the amplitude of the second mode of a laminated composite piezoelectric rectangular plate near the bifurcation. Figure 7 shows the effects of the detuning parameter \({\upsigma }_2 \) on the steady state amplitude of the second mode \(a_2\) for the parameters \({\upmu }_2 =0.2, {\upbeta }_4 =0.01, {\upomega }_2 =2.3, f_2 =2, f_{21} =0.1, f_{22} =0.2, f_{24} =0.3, \Omega _1 =1, \Omega _2 =1.2, \Omega _4 =1.4, {\upsigma }_1 =0.04\). It can be seen from Fig. 7 that maximum steady state amplitude occurs when \({\upomega }_2 \cong {\upomega }_1 \). Figure 8 shows that as the non-linear spring stiffness \({\upbeta }_4 \) is increased the continuous curve is moved downwards. The positive and negative values of \({\upbeta }_4 \), produce either softening or hardening behavior respectively. Figure 9 shows variation of the amplitude of the second mode \(a_2 \) with the detuning parameter \({\upsigma }_2 \) for various values of the external excitation force \(f_2 \). In this case, the amplitude behavior is softening. We note that increasing the external excitation force leads to increase on the steady state amplitude and multi-valued solutions.

Figures 10 and 11 show that the steady state amplitude \(a_2 \) is inversely proportional to \({\upmu }_2, {\upomega }_2 \). Also, for decreasing \({\upmu }_2, {\upomega }_2 \) the curve is bending to the left producing softening behavior.

Figures 12, 13, 14, 15, 16, 17, 18, 19, 20 and 21, show the response of the third case \(a_1 \ne 0, a_2 \ne 0\) of simultaneous primary and internal resonance \(\Omega _3 \cong {\upomega }_1, \upomega _2 \cong {\upomega }_1 \) against detuning parameter \({\upsigma }_2 \). Figure 12 represents the main figure for the case of primary resonance in the presence of one-to-one internal resonance for the parameters \({\upmu }_1 =0.2, {\upmu }_2 =0.2, {\upalpha }_1 =0.05, {\upalpha }_2 =0.01,{\upalpha }_3 =0.02,{\upalpha }_4 =0.03,{\upbeta }_1 =0.02,\) \({\upomega }_1 =\upomega _2 =2.3, f_1 =f_2 =2\). Each mode has two branches, which are stable and unstable solutions. For increasing external excitations \(f_1 \) and \(f_2 \) we observe that the first and second modes have increasing magnitude and the upper branch of the first and second mode intersect with the lower branch, as shown in Figs. 13 and 14. The steady state amplitudes of the first and second modes are decreasing and increasing for decreasing non-linear stiffness \({\upalpha }_1 \), and the upper branch becomes stable as shown in Fig. 15. Figure 16 shows that for increasing nonlinear parameter \({\upbeta }_1 \) the steady state amplitudes of the two modes are decreased. For increasing natural frequencies we show that the lower branch becomes unstable and upper branch becomes stable and the steady state amplitudes of the first and second are increased as obtained in Fig. 17.

Figure 18 shows that the effects of the detuning parameter \({\upsigma }_1 \) on the amplitudes of the two modes. The two branches for both modes have stable and unstable solutions.

When \({\upalpha }_2 \) is increased up to 0.5, we observe that both modes have the magnitudes as in Fig. 18, i.e. both modes do not affect by increasing \({\upalpha }_2 \) but the regions of stability are increased as shown in Fig. 19. For increasing nonlinear parameters \({\upalpha }_3, {\upalpha }_4 \) we show that the steady state amplitude of two modes is decreasing as shown in Figs. 20 and 21.

5.2 Comparison with the previous work

In the previous work [16], The Shilnikov type multi-pulse orbits and chaotic dynamics of a four-edge simply supported laminated composite piezoelectric rectangular plate subjected to the in-plane, transverse and piezoelectric excitations are investigated by using the energy phase method. The four-dimensional averaged equation in the case of primary parametric resonance and 1:3 internal resonances is obtained by using the method of multiple scales. Numerical simulations indicate that there exist different shapes of the chaotic responses for laminated composite piezoelectric rectangular plate under combined parametric and transverse excitations. It is found from numerical simulations that the shapes of the chaotic motions in the two modes are completely different.

In our study, the nonlinear analysis and stability of a composite laminated piezoelectric rectangular plate under simultaneous external and parametric excitation forces are investigated. The second-order approximation is obtained to consider the influence of the quadratic and cubic terms on non-linear dynamic characteristics of the composite laminated piezoelectric rectangular plate using the multiple scale method. All possible resonance cases are extracted at this approximation order. The analytical results given by the method of multiple time scale are verified by comparing them with results of numerical integration of the modal equations. The study is focused on the case of 1:1 internal resonance and primary resonance, where \({\upomega }_2 \cong {\upomega }_1 \) and \(\Omega _3 \cong {\upomega }_1 \). The stability of the system and the effects of different parameters on system behavior have been studied using frequency response curves. Variation of the some parameters leads to multi-valued amplitudes and hence to jump phenomena.

6 Conclusions

The method of multiple scales is used to obtain a uniform second-order expansion for rectangular symmetric cross-ply laminated composite plate subjected to external and parametric excitations. Second-order approximate solutions are obtained to study the influence of the cubic terms on non-linear dynamic characteristics of the composite laminated piezoelectric rectangular plate. All possible resonance cases are extracted at this approximation order. The study is focused on the case of 1:1 internal resonance and primary resonance, where \({\upomega }_2 \cong {\upomega }_1 \) and \(\Omega _3 \cong {\upomega }_1 \). The stability of linear and nonlinear solutions of the system is investigated. The frequency response curves are calculated to study the stability of the system. From the above study, the following may be concluded:

  • A comparison between the solutions obtained numerically with that prediction from the multiple scales show an excellent agreement.

  • Variation of the parameters \({\upalpha }_3, {\upbeta }_{4 }, f_1, f_2, {\upmu }_1, {\upmu }_2, {\upomega }_1, \upomega _2 \) leads to multi-valued amplitudes and hence to jump phenomena.

  • The multi-valued solutions are disappeared for increasing linear damping coefficients \({\upmu }_1, {\upmu }_2 \).

  • For the first and second modes, the steady state amplitudes \(a_1 \) and \(a_2 \) are directly proportional to the excitation amplitude \(f_1 \) and \(f_2 \), and inversely proportional to the linear damping \({\upmu }_1, {\upmu }_2 \) and natural frequencies \({\upomega }_1 \) and \({\upomega }_2 \).

  • The zone of instability increase, which is undesirable, for increasing excitation amplitude \(f_1, f_2 \) and for negative values of non-linear stiffness \({\upalpha }_{3}, {\upbeta }_4 \).

  • The zone of stability increase, which is desirable, for increasing non-linear parameters \({\upalpha }_1, {\upalpha }_2 \).

  • Negative and positive values of non-linear stiffness \({\upalpha }_{3}, {\upbeta }_4 \) produce either hard or soft spring respectively.