Discrete element simulation of powder compaction in cold uniaxial pressing with low pressure

Abstract

This paper presents numerical studies of powder compaction in cold uniaxial pressing. The powder compaction in this work is considered as an initial stage of a hot pressing process so it is realized with relatively low pressure (up to 50 MPa). Hence the attention has been focused on the densification mechanisms at this range of pressure and models suitable for these conditions. The discrete element method employing spherical particles has been used in the numerical studies. Numerical simulations have been performed for two different contact models—the elastic Hertz–Mindlin–Deresiewicz model and the plastic Storåkers model. Numerical results have been compared with the results of laboratory tests of the die compaction of the NiAl powder. Comparisons have shown that the discrete element method is capable to represent properly the densification mechanisms by the particle rearrangement and particle deformation.

1 Introduction

Uniaxial pressing is one of the techniques of powder compaction and consolidation. The uniaxial pressing involves compaction of powder into a rigid die by applying pressure in a single axial direction through a punch. Figure 1 shows a schematic of this process. In this work, the powder compaction is considered as the initial stage of the hot pressing process; thus, the process conditions are determined. The investigated uniaxial pressing is performed at an ambient temperature and under low pressure. The compaction of the powder in hot pressing is performed under pressure which is lower than that of conventional powder compaction and it is usually up to 50 MPa. Hence the attention has been focused on the densification mechanisms at this range of pressure and models suitable for these conditions.

Densification during powder compaction has an influence for overall manufacturing process. Success of hot pressing depends on the density and microstructure achieved during uniaxial pressing. Mechanical properties of the material after sintering and dimensional accuracy of the manufactured parts are related to the density obtained in the die compaction.

The process of powder pressing in a die is influenced by a number of factors, including particle size, shape, composition, and size distribution. The present paper is aimed to verify possibility to reproduce behaviour of a metallic powder under pressure using the discrete element model.

Powder compaction has been typically modelled using two different approaches: the continuum modelling and the discrete one. Different models of powder compaction are reviewed in [4, 25]. In the continuum approach, the porous powder under compaction is treated as a continuous medium at the macro-scale. Its deformation behaviour is usually described by phenomenological elastoplastic models. Different cap plasticity models are commonly used [3, 8]. In the phenomenological modelling, constitutive model parameters are obtained by fitting experimental data [3].

Discrete models are based on a discrete representation of the compacted powder. A number of discrete models of powder compaction have been developed within the framework of the discrete element method [21]. A model assuming rigid-plastic behaviour according to the Hollomon stress–strain curve has been developed by Storåkers et al. [26, 27]. The Storåkers model is based on the assumption of the rigid plasticity therefore the contact force has a plastic character from the contact initiation. More accurate elasto-plastic models, cf. [1, 24, 30], consider both the elastic and plastic ranges of the contact interactions. The discrete element method allows us to model interaction of very large collections of particles. The contact interaction and deformation of individual powder particles can be analysed; in this way the microstructure evolution during the compaction can be analysed [33].

Fig. 1

Schematic of uniaxial pressing

The powder compaction modelling in the present work is viewed upon as a preliminary step in simulation of the whole hot pressing process in which the stage of uniaxial pressing is followed by the stage of pressure assisted sintering. The discrete element method has also been used to model the powder sintering [9, 12, 14, 19, 32]. Most of these works, however, consider the unconstrained sintering in which there is no additional pressure. There are few investigations in which the DEM is used to model the pressure assisted sintering, cf. [9, 14, 18]. The attention in these works is concentrated more on a proper representation of sintering mechanisms than on modelling of the initial pre-sintering compaction. Since the results of the sintering stage depend on the initial conditions it is important to reproduce properly the die compaction being the initial stage of the whole manufacturing process. The present work is aimed to investigate the basic assumptions for the contact model of the powder compaction within a pressure range typical for the hot pressing. The elastic and plastic contact models will be studied. The numerical results will be compared with own experimental results.

2 Experimental studies

Uniaxial pressing of an intermetallic nickel aluminide (NiAl) powder has been studied experimentally. The same powder material has been used in experimental investigation of the complete hot pressing process presented in [2, 17]. Those studies were focused on the densification during the sintering stage. The present studies have been aimed to provide more details for validation of a numerical model of the compaction stage.

Morphology of the intermetallic powder used for the studies is shown in Fig. 2. It can be clearly seen that the powder particles are characterized by high sphericity. The particle size of the starting powder was analysed with the Clemex image analysing system. The particle size distributions of the intermetallic NiAl are presented in Fig. 3.

Fig. 2

Morphology of the NiAl powder before the compaction

Fig. 3

Particle size distribution of the NiAl powder

The bulk density of the powder has been determined by measuring the volume of a known quantity of the powder in the loose poured condition. The results of these measurements are shown in Fig. 4. The histogram shows the relative bulk density obtained in six measurements. The relative density is obtained as a ratio of the bulk density of the powder to the density of the NiAl material, 5910 kg/m$^3$. The relative density is equivalent to the packing fraction (or packing density) which is defined as a fraction of space occupied by the particles. Table 1 presents the statistical data of the measurements of the bulk density. The mean value of 0.65 has been obtained for the bulk relative density of the NiAl powder.

Fig. 4

Measurements of the relative bulk density of the NiAl powder

Table 1 Statistics of the relative bulk density measurements

Fig. 5

Evolution of the powder height and relative bulk density during the compaction process

The compaction tests have been performed on the press HP50-7010 Thermal Technology. The powder has been compressed in a graphite cylindrical die with a diameter of 10 mm with a pressure exerted by a punch. The pressure has been increased slowly (50 MPa has been achieved in 15 min) in order to obtain quasi-static conditions. Figure 5 shows the evolution of the powder height and relative bulk density as functions of the applied pressure. Evolution of the powder height in Fig. 5 is represented by the change of the powder height $\Delta H$ normalized with respect to the initial powder height $H_0=16.65$ mm. As can be seen, the densification of the powder has a nonlinear character. It is faster in the initial stage and slower in the final stage of the process. The initial growth of the powder density can be related mainly to the particles rearrangement. Contribution of the elastoplastic particle deformation becomes more important at higher values of the pressure; however, nonsmooth density evolution indicates that the particle rearrangement occurs not only in the initial stage of powder compaction, which is in agreement with observations of other researchers [11].

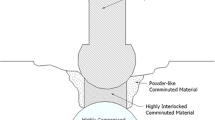
Figure 6 shows the morphology of the NiAl powder after the compaction process. It can be noticed that the particles have maintained the spherical shape. This indicates that the particle deformation at this level of pressure is small. Nevertheless, the traces of contacts can be noticed at some particles. The traces have been mainly produced by the indentation of small particles into bigger ones. This proves that the local stresses at contact points during the compaction exceed the yield stress.

Fig. 6

Morphology of the NiAl powder with visible traces of contacts after the compaction process

3 Discrete element model

3.1 Basic assumptions

A powder material is treated as an assembly of spherical particles whose translational and rotational motion is described by means of the Newton–Euler equations of rigid body dynamics. The equations of motion are integrated in time using an explicit central difference type algorithm, which is characterized with high efficiency of the solution at each time step. The known drawback of the explicit time integration scheme is its conditional numerical stability imposing the limitation on the time step.

Fig. 7

Rheological scheme of the contact model

The particles interact among one another with contact forces. Two different contact interaction models will be considered in this work. The first one is the Hertz–Mindlin–Deresiewicz model in which the normal interaction is described by a nonlinear relationship representing the elastic contact behaviour between two spheres. The second model will include the interaction law derived by Storåkers et al. [26, 27] assuming the plastic deformation of contacting spheres. A damping component will be included in the normal interaction force in both models. The tangential force will represent the effect of friction. A moment-type interaction or cohesion will not be taken into account. The detailed formulation of these contact models will be given below. The contact models have been implemented in the authors’ in-house version of the discrete/finite element code DEMpack [6].

3.2 Hertz–Mindlin–Deresiewicz model

We consider a dynamic contact of two spherical particles, i and j, with radii $R_i$ and $R_j$ from different materials. Assuming the elastic deformation of the particles we adopt the Hertz theory to describe the normal contact and the Mindlin–Deresiewicz model for the tangential contact interaction associated with the elastic deformation of the spheres [15]. Additionally, we introduce a viscous damping in the normal direction and a friction in the tangential direction as dissipative mechanisms. The rheological scheme of this model is shown in Fig. 7. The normal contact force $F_\mathrm{n}$ is a sum of the elastic force in the spring $F_\mathrm{n}^\mathrm{e}$ and the damping component $F_\mathrm{n}^\mathrm{d}$

$$\begin{aligned} F_\mathrm{n} = F_\mathrm{n}^\mathrm{e} + F_\mathrm{n}^\mathrm{d}\,. \end{aligned}$$

(1)

The elastic part of the normal contact force $F_\mathrm{n}^\mathrm{e}$ is evaluated according to the nonlinear Hertz equation

$$\begin{aligned} F_\mathrm{n}^\mathrm{e}=- \frac{4}{3}E^{*}\sqrt{R^*}|h|^{\frac{3}{2}}\,, \end{aligned}$$

(2)

where $E^*$ is the effective modulus of elasticity defined in terms of the Young’s moduli, $E_i$ and $E_j$, and the Poisson’s ratios, $\nu _i$ and $\nu _j$, of the two contacting particles

$$\begin{aligned} \frac{1}{E^*}=\frac{1-\nu _i^2}{E_i} + \frac{1-\nu _j^2}{E_j} \,, \end{aligned}$$

(3)

$R^*$ is the effective radius defined in terms of the particle radii, $R_i$ and $R_j$

$$\begin{aligned} \frac{1}{R^*}=\frac{1}{R_i} + \frac{1}{R_j} \,, \end{aligned}$$

(4)

and h is the particle overlap

$$\begin{aligned} h = d_{ij} - R_i - R_j\,, \end{aligned}$$

(5)

where $d_{ij}$ is the distance of the particle centres. Since no cohesion is allowed Eq. (2) is valid if $h\le 0$, otherwise $F_\mathrm{n}^\mathrm{e}=F_\mathrm{n}=0$.

The damping force $F_\mathrm{n}^\mathrm{d}$ is assumed to be a linear function of the normal relative velocity $v_\mathrm{rn}$

$$\begin{aligned} F_\mathrm{n}^\mathrm{d}=- c_\mathrm{n} v_\mathrm{rn} \end{aligned}$$

(6)

where $c_\mathrm{n}$ is the damping coefficient. The value of the damping coefficient $c_\mathrm{n}$ can be taken as a fraction $\xi$ of the critical damping $C_\mathrm{cr}$ for the system of two rigid bodies with masses $m_i$ and $m_j$, connected with a spring of the stiffness $k_\mathrm{n}$

$$\begin{aligned} c_\mathrm{n} = \xi C_\mathrm{cr} \end{aligned}$$

(7)

where the critical damping can be calculated as, cf. [29]:

$$\begin{aligned} C_\mathrm{cr}=2\sqrt{\frac{m_i m_j k_\mathrm{n}}{m_i+m_j} }\,. \end{aligned}$$

(8)

The normal stiffness $k_\mathrm{n}$ can be obtained as the derivative of the relationship (2)

$$\begin{aligned} k_\mathrm{n}= \frac{\displaystyle \mathrm{d}F_\mathrm{n}^\mathrm{e}}{\displaystyle \mathrm{d} h} =2E^{*}\sqrt{R^*|h|}\,. \end{aligned}$$

(9)

Using Eq. (2) in Eq. (9) the stiffness $k_\mathrm{n}$ can be written in terms of the force $F_\mathrm{n}^\mathrm{e}$

$$\begin{aligned} k_\mathrm{n}= \root 3 \of { \displaystyle 6{R^*}(E^{*})^2 | F_\mathrm{n}^\mathrm{e}| } \end{aligned}$$

(10)

The stiffness $k_\mathrm{n}$ will be used below to evaluate the damping coefficient.

The tangential contact force is calculated using an algorithm based on the Mindlin and Deresiewicz non-slip solution of the contact problem [15], which is commonly used in the framework of the DEM, cf. [7]. The tangential force ${\mathbf{F}}_{\mathrm{t}}$ is calculated incrementally, and its increments are given by the following expression

$$\begin{aligned} \Delta {\mathbf{F}}_{\mathrm{t}} = - k_{\mathrm{t}} \mathbf{v}_{\mathrm{rt}} \Delta t \end{aligned}$$

(11)

where $k_{\mathrm{t}}$ is the tangential stiffness, $\mathbf{v}_{\mathrm{rt}}$ is the relative tangential velocity and $\Delta t$ is the time step. The relative tangential velocity at the contact point depends on the linear and angular velocities of the contacting particles [23].

The tangential stiffness $k_{\mathrm{t}}$ depends on the particle overlap h

$$\begin{aligned} k_{\mathrm{t}} = 8 G^* \sqrt{\displaystyle {R^*}|h|} \end{aligned}$$

(12)

where ${R^*}$ is the equivalent radius defined by Eq. (4) and $G^*$ is the equivalent shear modulus

$$\begin{aligned} \frac{1}{G^*}=\frac{2-\nu _i}{G_i} + \frac{2-\nu _j}{G_j} \,. \end{aligned}$$

(13)

The tangential force ${\mathbf{F}}_{\mathrm{t}}$ is limited by the Coulomb friction

$$\begin{aligned} \Vert {\mathbf{F}}_{\mathrm{t}}\Vert \le \mu \ |F_\mathrm{n}| \ \,, \end{aligned}$$

(14)

where $\mu$ is the Coulomb friction coefficient.

Remark The contact model based on the Hertz and non-slip Mindlin–Deresiewicz theories, similar to the model described above, was labelled as H-MDns by Di Renzo and Di Maio [7]. These authors used the label H-MD for a model based on the implementation of the complete Mindlin–Deresiewicz theory for the tangential contact accounting more accurately for the effects of micro-slips. Further on, we will adopt the terminology of Di Renzo and Di Maio and we will use the name H-MDns for the model described above. The Hertz–Mindlin or Hertz–Mindlin–Deresiewicz theories are used in many implementations of contact models in the DEM [31]. The Hertz and Mindlin–Deresiewicz models are formulated for quasi-static contact problems, while in the DEM, we have a dynamic framework; therefore a dashpot providing viscous dissipation is usually incorporated in the Hertz–Mindlin–Deresiewicz models in the DEM in parallel to the spring representing the normal elastic interaction [5].

3.3 Storåkers model

The Hertz–Mindlin–Deresiewicz theory is valid for the elastic deformation while in powder compaction processes we usually deal with large deformation in which particles undergo the plastic deformation. The plastic deformation of the contacting spherical particles has been assumed in the model proposed by Storåkers et al. [26, 27]. This model considers a general viscoplastic behaviour combining strain hardening plasticity (for lower temperatures) and creep (for higher temperatures). Since the present work encompasses a quasi-static compaction at ambient temperature, only, our interest is limited to the plastic behaviour. Therefore a simplified formulation without strain rate effects is presented below.

Assuming the rigid-plastic properties of the particle materials are defined by the Hollomon stress–strain relationships

$$\begin{aligned} \sigma =\sigma ^{(a)}_0\varepsilon ^m\, \end{aligned}$$

(15)

where ${\sigma ^{(a)}_0}$, $a=i,j$, are material constants and m is the hardening exponent, the normal interaction force $F_\mathrm{n}^\mathrm{p}$ derived by Storåkers is given by the following Eq. [27]:

$$\begin{aligned} F_\mathrm{n}^\mathrm{p}= - 2^{1-m/2} 3^{1-m}\pi c^{2+m} \sigma ^*_0 (R^*)^{1-m/2} |h|^{1+m/2}\,, \end{aligned}$$

(16)

where $R^*$ is the effective radius defined by Eq. (4), h is the particle overlap given by Eq. (5), the parameter $c^{2+m}$ depends on the strain hardening exponent m:

$$\begin{aligned} c^{2+m}=1.43 \exp (-0.97 m) \end{aligned}$$

(17)

and the equivalent Hollomon constant $\sigma ^*_0$ is defined as follows

$$\begin{aligned} \left( \sigma ^{*}_0 \right) ^{ -{1/m}}= \left( \sigma ^{(i)}_{0} \right) ^{ -{1/m}} + \left( \sigma ^{{(j)}}_{0} \right) ^{ -{1/m}} \end{aligned}$$

(18)

The Storåkers model has been derived neglecting elastic deformation, cf. [10]. In such a model, unloading would be governed by the rigid behaviour (no change of deformation during unloading). A certain regularization would be necessary in the numerical algorithm in order to avoid non-unique force-displacement relationship during unloading. This is why Olsson and Larsson [20] combined the Storåkers model with the elastic unloading according to the Hertz model. This can be viewed upon as regularization of the Storåkers model. Our implementation follow the formulation presented [20]. The contact force during unloading is updated incrementally according to the following formula:

$$\begin{aligned} \Delta F_\mathrm{n}^\mathrm{p}= k^\mathrm{unl}_\mathrm{n} \Delta h \quad \text{ for }\quad \Delta h > 0\; \text{ and }\; h<0 \,, \end{aligned}$$

(19)

where $k^\mathrm{unl}_\mathrm{n}$ is defined analogously to Eq. (10):

$$\begin{aligned} k^\mathrm{unl}_\mathrm{n}= \root 3 \of { \displaystyle 6{R^*}(E^{*})^2 | F_\mathrm{n}^\mathrm{p}| }\,. \end{aligned}$$

(20)

Consequently, the total force during reoading is updated incrementally (until the previous maximum force is achieved) according to the elastic Hertz contact law.

The tangential contact force is evaluated assuming the regularized Coulomb friction model. The algorithm for calculation of the tangential force uses the incremental formula (11) with the tangential contact stiffness correlated to the normal stiffness:

$$\begin{aligned} k_{\mathrm{t}}= \beta k_\mathrm{n}^\mathrm{p}\,, \end{aligned}$$

(21)

where $\beta =0.5{-}5$ is suggested in [20], and the normal stiffness $k_\mathrm{n}^\mathrm{p}$ is determined as the derivative of the expression (16)

$$\begin{aligned}&k_\mathrm{n}^\mathrm{p}=\frac{ \mathrm{d} F_\mathrm{n}^\mathrm{p}}{\mathrm{d}h} = \left( 1+\frac{m}{2}\right) 2^{1-m/2} 3^{1-m}\pi c^{2+m}\nonumber \\&\quad \sigma ^*_0 (R^*)^{1-m/2} |h|^{m/2}\,. \end{aligned}$$

(22)

The constant value of the Coulomb friction coefficient $\mu$ is assumed in this work. A more accurate evaluation of the coefficient $\mu$ as a function of the angle of obliquity $\gamma = \mathrm{arc}\tan (v_{\mathrm{rt}}/v_\mathrm{rn})$ is proposed by Martin et al. [13].

3.4 Stability of time integration

Equations of motion in DEM are integrated in time using an explicit scheme. A known disadvantage of the explicit integration scheme is its conditional numerical stability imposing the limitation on the time step ${{\Delta t}}$, i.e.

$$\begin{aligned} {{\Delta t}} \le {{\Delta t}_\mathrm{cr}} \end{aligned}$$

(23)

where ${\Delta t}_\mathrm{cr}$ is a critical time step determined by the highest natural frequency of the system $\omega _\mathrm{max}$

$$\begin{aligned} {{\Delta t}_\mathrm{cr}}=\frac{2}{{\omega _\mathrm{max}}}\,. \end{aligned}$$

(24)

If damping exists, the critical time increment is given by

$$\begin{aligned} {{\Delta t}_\mathrm{cr}}=\frac{2}{{\omega _\mathrm{max}}}\left( \sqrt{ 1+\xi ^2}-\xi \right) \,, \end{aligned}$$

(25)

where $\xi$ is the fraction of the critical damping corresponding to the highest frequency $\omega _\mathrm{max}$.

Fig. 8

Particle settings for numerical studies a compression of two equal particles, b compression of three unequal particles

An exact calculation of the highest frequency $\omega _\mathrm{max}$ would require solution of the eigenvalue problem defined for the whole system of connected rigid particles. In practice, the critical time step is estimated taking the minimum value ${\Delta t}^\mathrm{min}_\mathrm{cr}$ of the critical time steps ${\Delta t}^{(i)}_\mathrm{cr}$ for independent mass–spring systems defined for each particle i with a certain safety margin specified by the parameter $\alpha$ ($0\le \beta < 1$):

$$\begin{aligned}&\Delta t \le \alpha {\Delta t}^\mathrm{min}_\mathrm{cr}\,, \end{aligned}$$

(26)

$$\begin{aligned}&{\Delta t}^\mathrm{min}_\mathrm{cr}=\min _i {\Delta t}^{(i)}_\mathrm{cr}\,, \end{aligned}$$

(27)

$$\begin{aligned}&{{\Delta t}^{(i)}_\mathrm{cr}}=\frac{2}{{\omega _{i}}}\left( \sqrt{1+\xi _{i}^2}-\xi _{i} \right) \,, \end{aligned}$$

(28)

$$\begin{aligned}&\omega _{i}= \sqrt{ \frac{k_{i}}{m_{i}} }\,. \end{aligned}$$

(29)

The value of $\beta$ has been studied by different authors. A good review can be found in [22], where the value close 0.17 is recommended for 3D simulation and 0.3—for a 2D case.

The stiffness $k_i$ for the calculation of the eigenfrequency according to Eq. (29) for the Hertz model is given by Eq. (9). Evaluation of the eigenfrequency for the Storåkers model requires consideration the type of loading. For the plastic loading, the stiffness $k_\mathrm{n}^\mathrm{p}$ given by Eq. (22) is taken, and for the elastic unloading/reloading, the stiffness $k^\mathrm{unl}_\mathrm{n}$ defined by Eq. (20) is taken. Thus, under the conditions of the elastic loading/reloading, the critical time step for the Storåkers contact model is the same as for the Hertz model.

A similar stability analysis can be performed for the rotational particle motion depending on the tangential stiffness. It can be shown that for equal values of the normal and tangential stiffness the rotational eigenfrequency is higher than the translational one [23]. In order to avoid the limitation imposed by the rotational eigenfrequency the rotational inertia of the particles in our simulations is scaled by factor 10.

4 Studies of particle interaction

Detailed studies of interaction of single NiAl particles under compression have been performed using the two contact models presented earlier, the elastic Hertz model and the plastic Storåkers one. The studies have been carried out for the particle settings shown in Fig. 8. In the first case (Fig. 8a), the compression of two equal particles with radii $R=10$ $\upmu \mathrm{m}$ has been analysed, while the other case (Fig. 8b) consists in compression of three particles aligned along a line, two of the particles are bigger ($R=10$ $\upmu \mathrm{m}$) and one of them, the middle one is smaller ($r=2$ $\upmu \mathrm{m}$). The assumed particle sizes are typical for the real powder particles, cf. Fig. 3.

The purpose of these studies was to: (i) identify the range of contact forces and particle deformations which can be expected in powder subjected to uniaxial compression under external pressure typical for hot pressing (up to 50 MPa), (ii) compare the force–indentation relationships for different models and model parameters, and (iii) explain experimental observations presented in Sect. 2.

The material properties of the NiAl are given in Table 2. The elastic properties have been determined in the authors’ own measurements [2], and the yield stress has been taken from [16]. The Storåkers model has been studied assuming the rigid-plastic behaviour without hardening and with strain hardening defined by three different exponents $m=0.05$, 0.1 and 0.2 in the Hollomon Eq. (15). All the stress–strain curves used in the Storåkers model are plotted in Fig. 9. The following pairs of the Hollomon constants have been investigated: (i) $m=0$, $\sigma _0=800$ MPa, (ii) $m=0.05$, $\sigma _0=1480$ MPa, (iii) $m=0.1$, $\sigma _0=1375$ MPa, (iv) $m=0.2$, $\sigma _0=2363$ MPa. The Hollomon constants $\sigma _0$ corresponding to the strain hardening exponents m have been evaluated assuming that all the curves pass through the point corresponding to the yield point in the elasto-plastic model: $(\sigma _Y/E, \sigma _Y)$.

Table 2 Material properties of NiAl

Fig. 9

Stress–strain curves for the Storåkers model

The compressive loading has been introduced by prescribing the displacements to the particle centres. In the second case, the displacement has been applied to the bigger particles, only. The displacement-driven loading has been applied with a constant velocity $10^{-4}$ m/s. Quasistatic loading conditions have been assumed so no damping has been considered. No rotation and no shear have been taken into account. The evolution of the contact forces F predicted by the Herz and Storåkers models as functions of the particle overlap (indentation) h is shown in Figs. 10 and 11 for compression of two and three particles, respectively. Figure 12 shows the critical time step evolution for compression of two particles.

Fig. 10

Force versus indentation curves for compression of two equal spheres for different contact models

Fig. 11

Force versus indentation curves for compression of three spheres for different contact models

Fig. 12

Critical time step versus indentation curves for compression of two equal spheres for different contact models

It is seen in Figs. 10 and 11 that initially the Hertz model predicts a softer behaviour; however, its response gets stiffer quickly and the stiffness of the Hertz contact becomes higher than that of the Storåkers model. The stiffness in the Storåkers model depends the exponent m. With the increasing exponent m, the response predicted by the Storåkers model gets stiffer. The critical time step evolution is correlated with the model stiffness. It is seen in Fig. 12 that initially when the stiffness in the Hertz model is smaller the critical time step is higher than in the Storåkers models. The critical time step gets smaller when the stiffness increases.

The Storåkers model is based on the assumption of the rigid plasticity; therefore, the contact force has a plastic character from the contact initiation. If we consider both the elastic and plastic ranges of the contact interactions, the transition between these ranges can be defined by the incipient yielding. The Hertz contact force corresponding to the onset of the yield in the contact of two equal spheres is given by the following formula:

$$\begin{aligned} F_Y=(1.61)^3 \frac{\pi ^3 R^2(1-\nu ^2)^2}{6E^2}\sigma _Y^3 \end{aligned}$$

(30)

obtained assuming the Mises yield criterion [31]. The indentation producing incipient yielding can be obtained by inverting Eq. (2) and substituting the value of the force calculated from Eq. (30). The point ($h=2.09 \times 10^{-9}$ m, $F= 2.822 \times 10^{-5}$ N), calculated in this way, representing the onset of yielding is plotted in Fig. 10. It can be seen that the yielding is initiated at very low values of indentation and force. A further increase of the compressive loading is associated with an increase of the plastic zone in the contact area and development of the plastic deformation in the sphere volume. Since the range of purely elastic deformation is very small it is justified to neglect it and apply the Storåkers model based on the assumption of the rigid-plastic deformation of the contacting spheres. It can be observed, however, that in the initial range the Storåkers model predicts a higher contact force than the elastic Hertz model. This is contradictory to the expectation that the plastic response should be softer than the elastic one. This problem can be cured simply by taking a minimum of the two forces, the one predicted by the Hertz elastic model and the other one given by the Storåkers plastic model, as it was done by Martin et al. [13]. On the other hand, the difference between the forces predicted by the two models is relatively small. The effect of the model will be studied in the next section for a specimen consisting of a large number of particles.

Now, we will determine a level of the forces and indentation which can be expected in compression in a real process of hot pressing. For this purpose, let us transform the equations defining the forces in the Hertz and Storåkers models. Let us divide both sides of Eqs. (2) and (16) by $4R^2$. Taking $F_\mathrm{n}^{e}=F$, $E^*=E/(2(1-\nu ^2))$ and $R^*=R/2$ Eq. (2) can be rewritten as follows:

$$\begin{aligned} \frac{F}{4R^2}=- \frac{1}{3}\frac{E}{1-\nu ^2} \left( \frac{|h|}{2R} \right) ^{\frac{3}{2}}\,. \end{aligned}$$

(31)

Similarly, Eq. (16) can be rewritten as follows:

$$\begin{aligned} \frac{F}{4R^2} = - 2^{1-m/2} 3^{1-m}\pi c^{2+m} \sigma _0 \left( \frac{|h|}{2R} \right) ^{1+m/2}\,. \end{aligned}$$

(32)

It can be easily noted that the pressure-type parameter $F/4R^2$ can be a reasonable estimate of the external pressure exerted on the particle assembly which is illustrated graphically in Fig. 8a. The parameter $F/4R^2$ would give exactly an external pressure for a regular cubic arrangement of equal spheres. Equations (31) and (32) express the pressure as functions of the dimensionless parameter |h| / 2R. Taking advantage of these equations, the force–displacement diagrams in Fig. 10 can be alternatively presented as the relationships $(F/4R^2)$ versus (|h| / 2R). The respective axes are scaled appropriately in Fig. 10.

Fig. 13

Generation of the geometrical model a filling the container with loose particles, b the cylindrical container with settled particles

The graphs in Fig. 10 allow us to estimate values of contact forces and particle deformations induced by a given external pressure exerted on an assembly of equal spheres. It can be found that the external pressure of 50 MPa exerted on an assembly of spheres with radii of 10 $\upmu$m can produce contact interactions of around 0.02 N and the indentation between the spheres according to the considered models is around 0.8–0.9% of the diameter. The indentation is very small, and so must be the deformation of the powder particle in the performed tests when they are in contact with other particle of a similar size. This can explain why the deformation of the powder particles after tests in Fig. 6 is barely visible.

A similar analysis can explain traces of the contact with smaller particles. Let us assume a similar value (0.02 N) of the contact force for the compression of three spheres shown in Fig. 8b. Then, the indentation between spheres with radii 10 and 2 $\upmu$m predicted by the Storåkers model (Fig. 11) is around 0.4–0.5 $\upmu$m (around 10–12.5% of the smaller particle diameter) and it is much larger than the indentation between spheres with equal radius of 10 $\upmu$m. If similar arrangements of particles (a small particle compressed between two larger ones) occur in a compressed powder, traces due to plastic indentation appear on the surfaces of the larger particles. The force–indentation diagrams in Fig. 11 show that in this case the difference between the elastic and plastic models for the level of expected forces is significant. The traces due to plastic deformation observed in the real powder indicate that the contact interaction assuming plasticity is more appropriate in this case.

Fig. 14

Particle size distribution in the discrete element model a number distribution, b volume distribution

5 Simulation of powder compaction in a cylindrical die

The die compaction process of the intermetallic NiAl powder, investigated experimentally in Sect. 2, has been studied numerically using the models presented in Sect. 3. Simulations have been performed using a reduced cylindrical specimen and keeping the real size and size distribution of the powder particles shown in Fig. 14. The specimen has been generated using a dynamic technique. A set of 1751 loose particles of diameters ranging from 1.5 to 18.5 $\upmu$m randomly distributed in space has been generated and poured through a funnel (Fig. 13a) to a cylindrical container of diameter 58 $\upmu$m. The cylindrical sample formed by the particles settled under gravity is shown in Fig. 13b. The simulation of this stage has been performed assuming the frictionless Hertz contact model with the elastic properties given in Table 2. A very small friction coefficient, 0.02, has been assumed for the contact between the particles and the walls of the cylinder in simulation of powder filling as well as pressing.

The particles have been generated using the real particle size distribution shown in Fig. 3. Due to a small size of the numerical specimen, the biggest particles of the intermetallic powder ($d_\mathrm{p} >20\,\mathrm {\upmu }$m) were not considered in the numerical model. The particle size distribution in the discrete element model according to the number and volume of particles is presented in Fig. 14a, b, respectively. The numerical distribution according to the number in Fig. 14b is compared with the experimental distribution, showing a good coincidence.

The top surface of the specimen shown in Fig. 13b has been flattened by the plate representing the punch under a prescribed small displacement of 3 $\upmu$m downwards from the first contact with particles (Fig. 15) and then unloaded. The height, $H_0= 95$ $\upmu$m, of the flattened specimen after unloading has been used to determine the initial specimen volume and the initial bulk density in the numerical model. The initial relative bulk density, 0.62, has been determined in this way.

This value is slightly lower than 0.65, the relative density obtained experimentally in the poured condition. We can suspect, however, that this value is strongly influenced by the so-called wall effect. The container wall affects a local packing structure of particles and the porosity near the wall is higher than in the centre of the container [28]. This decreases the value of the average bulk density calculated for the powder specimen. This effect is especially important for small containers and specimens.

In order to overcome this problem, an alternative way to calculate the bulk density based on the concept of the representative volume element (RVE) has been proposed here. A spherical RVE with the centre coinciding with the centre of the cylindrical sample has been introduced (Fig. 15). The diameter of the RVE, 54 $\upmu$m, has been assumed as possibly large and suitable to avoid the zone affected by the wall effect. The solid fraction in the RVE has been calculated exactly using analytical formulae for the intersection of the spheres. The relative bulk density of 0.66 has been determined for the RVE, which is a little higher than the experimental value. In further studies, the densities determined in both ways will be given.

Fig. 15

Idea of the bulk density evaluation

Fig. 16

Simulation of die compaction using the Hertz contact model a 0 MPa, b 2 MPa, c 25 MPa, d 50 MPa.

The particle specimen generated in this way has been used in simulations of the die compaction. The powder has been subjected to the compression exerted by the plate (Fig. 16) loaded with a linearly rising pressure from 0 to 50 MPa in time of $10^{-4}$ s. An appropriate damping (damping coefficient $\xi =0.9$) ensured a quasi-static character of the compaction process. The time integration has been carried out using the time steps estimated according to the procedure explained in Sect. 3.4 with the safety coefficient $\alpha =0.1$. The analyses have been performed assuming the Hertz–Mindlin–Deresiewicz and Storåkers models with the parameters used in the studies described in Sect. 4. The elastic material properties for the Hertz model are given in Table 2. The Storåkers model has been used with the following pairs of the Hollomon constants: (i) $m=0$, $\sigma _0=800$ MPa, (ii) $m=0.1$, $\sigma _0=1375$ MPa, (iii) $m=0.2$, $\sigma _0=2363$ MPa. The problem has been studied without and with friction. Figure shows the results of the simulation for the frictionless Hertz contact model. The reduction of the specimen height can be clearly observed. The change of the specimen height normalized with respect to the initial height $H_0$ obtained for all the analysed cases with zero friction is plotted in Fig. 17. The results are compared with the experimental data showing quite a good agreement.

The curves showing the relative density as functions of the applied pressure are given in Fig. 18. The numerical results in Fig. 18 have been obtained for the Hertz and Storåkers models with zero friction conditions. The bulk density has been obtained by averaging over the specimen and RVE. It can be noticed that averaging over the specimen gives lower values of the bulk density. Averaging over the RVE gives values very close to the experimental results. Having in mind that the averaging over the specimen volume is affected by the wall effect the numerical results based on the RVE averaging are more trustworthy. The evolution of the bulk density predicted in numerical simulations is similar to that determined experimentally. We have a high densification rate in the initial phase caused by particle rearrangement and the density changes slower in the later phase, at a higher density, when the rearrangement of the particles is more difficult. Then, the deformation of the particles becomes a more important densification mechanism. Differences between the numerical results obtained with different models are relatively small. This is because the differences between the force–indentation curves predicted by the compared models in the range of contact pressure in our studies are relatively small, cf. Fig. 10.

Zero friction conditions are favourable for particle rearrangement. The effect of friction on the densification rate has been studied for both numerical models. The relative density evolution for different friction coefficients ($\upmu =0, 0.01, 0.02$ and 0.05) for the Hertz–Mindlin–Deresiewicz and Storåkers ($m = 0.2$) models is shown in Figs. 19 and 20, respectively. It can be noticed that with the increase of friction the change of the density in the initial phase decreases. This means that friction resisting particle sliding creates mechanical locking between particles and blocks particle rearrangement. This effect is clearly visible even for relatively small friction coefficients. The friction coefficient is one of the model parameters which should be determined in model calibration. The results of the sensitivity studies presented in Figs. 19 and 20 show that changing the friction coefficient allows us to tune the numerical density evolution to the experimental results.

Fig. 17

Evolution of the specimen height during die compaction (numerical results for zero friction)

Fig. 18

Relative density as a function of pressure—comparison of the numerical results for zero friction with the experimental data

Fig. 19

Relative density as a function of pressure for the Hertz–Mindlin–Deresiewicz model with different friction coefficients

Fig. 20

Relative density as a function of pressure for the Storåkers model ($m = 0.2$) with different friction coefficients

6 Concluding remarks

The present work has been aimed to verify and validate discrete element models of powder compaction. The present work has been focused on the die compaction under a relatively low pressure. Experimental investigations of the die compaction of the NiAl powder have been performed in order to provide data for validation of numerical models.

The range of contact forces and pressure expected in compaction with a pressure up to 50 MPa has been identified, and possible particle deformation has been estimated assuming the elastic and plastic deformation. It has been shown that yielding at the contact is initiated at an early stage of the compression but the particle deformation at a low pressure is relatively small, especially in contact between equal particles. It has been shown that a more significant deformation can be produced between particles of different sizes. This has been confirmed by microscopic observations of the NiAl powder after compaction.

Numerical simulations of the die compaction have been performed for a reduced size specimen of particles with the size and size distribution the same as in the real powder. The use of the reduced specimen required a careful evaluation of averaged density in order to avoid the wall effect. Numerical evolution of the bulk density under pressure has been compared with experimental results. The comparisons have shown that under investigated range of pressure both models, the elastic Hertz model and the plastic Storåkers model, produce quite similar macroscopic behaviour. Nevertheless, studies of the local stresses indicate that the plastic Storåkers contact model is more suitable to represent a local interaction associated with yielding at the contact point.

The effect of the friction has also been investigated. It has been shown that the friction between particles can block their rearrangement. The results of the present work have confirmed that the spherical discrete element method is a suitable tool to model powder compaction.