1 Introduction

Streamflow forecasting is the process of estimating future streamflow in advance, based on available information. Timely streamflow may help the public to reduce the impacts of a flood or a drought. As streamflow is stochastic, time series analysis is a widely used method for streamflow forecasting. The most widely used models are autoregressive (AR) or autoregressive moving average (ARMA) models, which have been applied for forecasting streamflow under different conditions (Carlson et al. 1970; Haltiner and Salas 1988; Jones and Brelsfor 1967; Salas and Obeysekera 1982). However, the underlying linear assumption of these methods is the major drawback that sometimes limits their application (Elshorbagy et al. 2002). On the other hand, it has been shown that spectral analysis is capable of extracting significant information for understanding the streamflow process and prediction thereof (Fleming et al. 2002; Ghil et al. 2002; Labat 2005; Marques et al. 2006; Molenat et al. 1999). Thus, entropy theory is employed to combine spectral analysis and time series analysis for streamflow forecasting.

The development of Burg entropy spectral analysis (BESA) (Burg 1967, 1975) not only improved the resolution of the spectral density but also improved the reliability of prediction of streamflow. BESA has been applied to forecast hydrological series and it is recommended over classical methods (Krstanovic and Singh 1989, 1991a, b; Singh 2013). However, due to the weakness in determining multi-peak spectral density for non-stationary conditions (Boshnakov and Lambert-Lacroix 2012), it sometimes does not work well for monthly streamflow with strong seasonal and periodic characteristics.

The configurational entropy spectral analysis (CESA) was introduced by Frieden (1972) and Gull and Daniell (1978), which is sometimes also referred to as maximum entropy method 2 (MEM2) or spectral MESA (SMESA) (Katsakos-Mavromichalis et al. 1985; Tzannes et al. 1985; Tzannes and Avgeris 1981). Superior to BESA, CESA has been shown to be not restricted to the AR process (Liefhebber and Boekee 1987; Ortigueira et al. 1981). Configurational entropy has also been applied for spectral analysis and shown to have a better resolution than BESA for autoregressive moving average (ARMA) and moving average (MA) processes, and is comparable to BESA for the autoregressive (AR) process (Nadeu et al. 1981). It has been applied to forecast monthly streamflow and has shown better reliability than BESA for both high flow and low flow (Cui and Singh 2015).

Besides, there is relative entropy spectral analysis (RESA), which was developed by Shore (1979, 1981) as an extension of Burg’s maximum entropy spectral analysis, where the spectral power was considered as a random variable. RESA can be used for streamflow forecasting as well. Later, another version of RESA was developed by Tzannes et al. (1985), considering frequency as a random variable. The RESA spectra are reported to have higher resolution and are more accurate in detecting peak location than other methods for spectral computation (Papademetriou 1998). Besides, the RESA theory reduces the number of prediction coefficients by relying on the prior information (Schroeder 1982). However, RESA has not been applied to streamflow forecasting yet.

The objective of this paper is to review and compare three methods of entropy spectral analysis, which are Burg entropy spectral analysis (BESA), configurational entropy spectral analysis (CESA) and relative entropy spectral analysis (RESA).

2 Entropy Spectral Analyses

Let streamflow time series y(t) be denoted as y1,…, yT, where T is the total time period. Transferring to the frequency (f) domain, the information on streamflow is stored in the spectral density p(f). Considering frequency f as a random variable, the normalized spectral density p(f) can be taken as the probability density function. Thus, the Burg entropy can be defined as

$$ {H}_B(f)={\displaystyle \underset{-W}{\overset{W}{\int }} \ln \left[p(f)\right]df} $$
(1)

where W = 1/(2Δt) is the Nyquist fold-over frequency and f is the frequency that varies from –W to W, Δt is the sampling period. It is observed that the Burg entropy is defined as the sum of log of the spectral density values.

Taking the expectation of the integral of the log of spectral density, the configurational entropy is defined as

$$ {H}_C(f)=-{\displaystyle \underset{-W}{\overset{W}{\int }}p(f) \ln \left[p(f)\right]df} $$
(2)

On the other hand, with given prior spectral density q(f), the relative entropy of the spectral density p(f) can be defined as

$$ {H}_R(f)={\displaystyle \int p(f) \ln \left[p(f)/q(f)\right]df} $$
(3)

The prior spectral density can be taken as a background noise with the peak assumed at the observed periodicity. It is noted that when a uniform prior is taken, the relative entropy reduces to the configurational entropy.

The development of entropy spectral analyses comprises the following steps: (1) derivation of entropy-based spectral density, (2) computation of the Lagrange multipliers, (3) extension of the autocorrelation function, and (4) forecasting of streamflow.

2.1 Derivation of Entropy-Based Spectral Density

To obtain the least biased spectral density, one needs to maximize the Burg and configurational entropy but minimize the relative entropy to the prior subject to specified constraints. The constraints can be formed from the relationship between the spectral density and autocorrelation, which can written as

$$ {\rho}_n={\displaystyle \underset{-W}{\overset{W}{\int }}p(f){e}^{i2\pi fn\varDelta t}df},-N\le n\le N $$
(4)

where \( i=\sqrt{-1} \) and ρ n is the autocorrelation function of n-th lag. When n = 0, Eq. (4) reduces to

$$ {\rho}_0={\displaystyle \underset{-W}{\overset{W}{\int }}p(f)df=1} $$
(5)

Thus, entropy can be maximized or minimized, subject to the constraints, using the Lagrange multipliers, in which the Lagrangian function can be formulated as

$$ L(f)=H(f)-{\displaystyle \sum_{n=-N}^N{\lambda}_n\left[{\displaystyle \underset{-W}{\overset{W}{\int }}p(f) \exp \left(i2\pi fn\varDelta t\right)df}-{\rho}_n\right]} $$
(6)

where λ n , n = 0, 1, 2, …, N, are the Lagrange multipliers, and H(f) is the entropy to be maximized [as H B (f) or H C (f)] or to be minimized [as H R (f)]. Taking the partial derivative of L(f) with respect to the spectral density and equating to zero, \( \frac{\partial L(f)}{\partial p(f)}=0 \), the least-biased spectral densities obtained from the maximization of the Burg entropy and configurational entropy and from the minimization of the relative entropy, respectively, are

$$ {p}_B(f)=\frac{1}{{\displaystyle \sum_{n=-N}^N{\lambda}_n{e}^{-i2\pi fn\varDelta t}}} $$
(7)
$$ {p}_C(f)= \exp \left(-1-{\displaystyle \sum_{n=-N}^N{\lambda}_n{e}^{i2\pi fn\varDelta t}}\right) $$
(8)
$$ {p}_R(f)=q(f) \exp \left(-1-{\displaystyle \sum_{n=-N}^N{\lambda}_n{e}^{i2\pi fn\varDelta t}}\right) $$
(9)

It can be seen from the above three equations that the spectral density derived from the Burg entropy is in the form of inverse of polynomials, while the ones from the configurational entropy and relative entropy are in the exponential form. The form in Eq. (7) suggests that BESA is related to the linear prediction process.

2.2 Determination of Parameters

Due to the different forms of the spectral density, the ways of determining Lagrange multipliers are different. For the Burg entropy, the Lagrange multipliers and prediction coefficients can be computed from the Levinson-Burg algorithm developed by Burg (1967, 1975). The Levinson-Burg algorithm is a recursive algorithm for estimating prediction coefficients, and improves the original Levinson algorithm by computing forward and backward prediction error together to update the coefficient of next order (Collomb 2009; Lin and Wong 1990).

However, for the configurational entropy and relative entropy, the cepstrum analysis is incorporated. Taking the inverse Fourier transform of the log-magnitude of Eq. (9), one obtains

$$ {\displaystyle \underset{-W}{\overset{W}{\int }}\left\{1+ \log \left[p(f)\right]- \log \left[q(f)\right]\right\}{e}^{i2\pi fn\varDelta t}df}={\displaystyle \underset{-W}{\overset{W}{\int }}\left(-{\displaystyle \sum_{n=-N}^N{\lambda}_n{e}^{i2\pi fn\varDelta t}}\right){e}^{i2\pi fn\varDelta t}df} $$
(10)

It can be seen from Eq. (10) that there are two terms relating to the spectral density that can turn to the cepstrum of autocorrelation, which is also called autocepstrum.

Let the prior cepstrum of autocorrelation be denoted as e q.(n), which is transferred from the prior spectral density as

$$ {e}_q(n)={\displaystyle \underset{-W}{\overset{W}{\int }} \log q(f){e}^{i2\pi fn\varDelta t}df} $$
(11)

Similarly, the posterior cepstrum of autocorrelation e p (n) transform from the posterior spectral density can be expressed as

$$ {e}_p(n)={\displaystyle \underset{-W}{\overset{W}{\int }} \log p(f){e}^{i2\pi fn\varDelta t}df} $$
(12)

Doing the integration of both sides of Eq. (10), one gets

$$ {\delta}_n+{e}_p(n)-{e}_q(n)=-{\displaystyle \sum_{s=-N}^N{\lambda}_s{\delta}_{n-s}} $$
(13)

where δ n is the delta function defined as:

$$ {\delta}_n=\left\{\begin{array}{cc}\hfill 1,\hfill & \hfill n=0\hfill \\ {}\hfill 0,\hfill & \hfill n\ne 0\hfill \end{array}\right. $$
(14)

Equation (13) can be expanded as a set of N linear equations:

$$ \begin{array}{c}\hfill {\lambda}_0=-1-{e}_p(0)+{e}_q(0)\hfill \\ {}\hfill {\lambda}_1=-{e}_p(1)+{e}_q(1)\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill {\lambda}_k=-{e}_p(k)+{e}_q(k)\hfill \end{array} $$
(15)

Equation (15) enables to solve for the Lagrange multipliers in a straight-forward manner. Thus, the Lagrange multipliers can be estimated from the summation of the prior and posterior autocepstrums. The prior autocepstrum can be obtained from the observed periodicity of streamflow. The posterior autocepstrum can be estimated from the following recursive function introduced by Nadeu (1992) as

$$ {e}_p(n)=2\left[\rho (n)-{\displaystyle \sum_{k=1}^{n-1}\frac{k}{n}{e}_p(k)}\rho \left(n-k\right)\right]\begin{array}{cc}\hfill, \hfill & \hfill n\hfill \end{array}>0 $$
(16)

It is seen from Eq. (16) that the nth lag of cepstrum e p (n) is dependent on the previous n-1 lags of cepstrum and n-lags of autocorrelation. Thus, for given N lag autocorrelations, the cepstrum of autocorrelation can be computed up to lag N.

It can be noted that for solving parameters of the configurational entropy without prior, the cepstrum e q in Eq. (15) equals 0 and diminishes, and the Lagrange multipliers are solved from

$$ \begin{array}{c}\hfill {\lambda}_0=-1-{e}_p(0)\hfill \\ {}\hfill {\lambda}_1=-{e}_p(1)\hfill \\ {}\hfill \vdots \hfill \\ {}\hfill {\lambda}_k=-{e}_p(k)\hfill \end{array} $$
(17)

where e p (n) is computed from Eq. (16) as well.

2.3 Extension of Autocorrelation

According to Burg’s (1967, 1975) derivation, maximization of the Burg entropy allows the autocorrelation to be extended as a linear combination of previous lags with the prediction coefficients as

$$ {\rho}_{N+k}=-{\displaystyle \sum_{j=1}^m{\rho}_{N+k-j}{a}_j} $$
(18)

On the other hand, for the configurational entropy and relative entropy, the autocorrelation is extended with the inverse relationship of Eq. (16) using the autocepstrum as

$$ {\rho}_{N+k}=\frac{e_p\left(N+k\right)}{2}+{\displaystyle \sum_{j=1}^m\frac{k}{N+k}{e}_p(j)}\rho \left(N+k-j\right) $$
(19)

When no prior is given, Eq. (19) reduces to

$$ {\rho}_{N+k}={\displaystyle \sum_{j=1}^m\frac{k}{N+k}e(j)}\rho \left(N+k-j\right) $$
(20)

2.4 Streamflow Forecasting

Streamflow is forecasted in the manner that autocorrelation function is extended. Thus using BESA, streamflow is forecasted by a linear combination of past series weighted by the coefficients in Eq. (18) to extend the autocorrelation, which becomes

$$ {y}_{T+1}={a}_1{y}_T+{a}_2{y}_{T-1}+\dots +{a}_m{y}_{T+m-1} $$
(21)

When using CESA or RESA, streamflow is forecasted with cepstrum analysis which is the way autocorrelation is extended. Thus, streamflow is forecasted by

$$ {y}_{T+k}=\frac{c_p\left(T+k\right)}{2}+{\displaystyle \sum_{j=1}^m\frac{k}{T+k}{c}_q(j)}y\left(T+k-j\right) $$
(22)

where c(j) is the cepstrum of the time series and equals to \( \frac{1}{2}e(n) \). Then Eq. (22) can be written as

$$ {y}_{T+k}=\frac{1}{4}{e}_p\left(N+k\right)+\frac{1}{2}{\displaystyle \sum_{j=1}^m\frac{k}{T+k}{e_{\hbox{'}}}_q(j)}y\left(T+k-j\right) $$
(23)

When no prior is given, e p is 0, thus, streamflow forecasted by CESA becomes

$$ {y}_{N+k}=\frac{1}{2}{\displaystyle \sum_{j=1}^m\frac{k}{T+k}e(j)}y\left(T+k-j\right) $$
(24)

The order of forecasting model m is identified by the Akaike information criterion (AIC) or the Bayesian information criterion (BIC) (Box and Jenkins 1970; Hipel and McLeod 1994).

3 Application

The proposed three entropy spectral analysis methods, BESA, CESA and RESA, are verified using observed streamflow data from Iowa River. Iowa River is a tributary of Mississippi River, which is about 520 km long and has a drainage area of 33,000 km2. Two stations are chosen for comparison, one from the upstream and the other from the downstream. The upstream station of Iowa River has a mean monthly streamflow of 9.3 m3/s, while the downstream station has a mean of 305 m3/s.

3.1 Estimation of Spectral Density

First of all, the spectral densities, estimated by BESA, CESA and RESA, are compared to the one estimated from the Fast Fourier transform (FFT), as plotted in Fig. 1. As seen from the figure, the spectral density of the upstream station is more likely to be multi-peaked than that of the downstream station. For the upstream station, spectral peaks at frequencies 1/12th, 1/6th and 1/4th are significant and even peaks at frequencies 1/3th, 5/12th and 1/2th are visible. However, for the downstream station, there are no more peaks after frequency 1/4th. The performance of the three entropy spectral analyses was evaluated by the Itakura-Saito distortion, which is a measure of the perceptual difference between an original spectrum and its estimate. The distortion is defined as

$$ {D}_{I-S}\left(\widehat{p}(f),p(f)\right)=\frac{1}{2\pi }{\displaystyle \int \left[\frac{p(f)}{\widehat{p}(f)}- \log \left(\frac{p(f)}{\widehat{p}(f)}\right)-1\right]}df $$
(25)

where p(f) represents the spectral density from FFT and \( \widehat{p}(f) \) is the estimated spectral density. The smaller value represents a better fit.

Fig. 1
figure 1

Spectral density estimated by three entropy spectral analysis methods for a an upstream station on Iowa River and b a downstream station on Iowa River

Full size image

As seen in Fig. 1, BESA did not perform well in estimating the spectral density with multi-peaks. BESA estimated spectral peaks at frequencies 1/12th and 1/6th with the same significance for the upstream station and estimated spectral peaks at frequency 1/6th with higher significance than at 1/12th frequency. However, for monthly streamflow of Iowa River, the 12 month periodicity is the most important periodicity, and should always be most significant. On the contrary, the CESA and RESA methods correctly estimated the most significant peak at 1/12th frequency. One concern of CESA is that it ignores all less significant peaks to keep the peak at 1/12th frequency most significant. Though, using RESA, those less significant peaks were estimated, and were found to be consistent to the ones from FFT.

The Itakura-Saito distortion, listed in Table 1, had the largest values using BESA and smallest values using RESA for both upstream and downstream stations. Besides, the difference between BESA and CESA was larger than that between CESA and RESA. It suggests that for streamflow of Iowa River, the exponential form of CESA and RESA fits better than the polynomial form of BESA.

Table 1 Itakura-Saito distance of estimated spectral density
Full size table

3.2 Forecasted Streamflow

Streamflow was forecasted by the three entropy spectral analysis methods with a 3 year lead time for an upstream station and a 1 year lead time for a downstream station on Iowa River, as shown in Fig. 2. The goodness of forecasting was examined by RMSE, r 2 and NSE, which are defined as

$$ RMSE=\sqrt{\frac{{\displaystyle \sum_{i=1}^N{\left({Q}_o(i)-{Q}_f(i)\right)}^2}}{N-1}} $$
(26)
$$ {r}^2={\left\{\frac{{\displaystyle \sum_{i=1}^N\left({Q}_o(i)-\overline{Q_o}\right)\left({Q}_f(i)-\overline{Q_f}\right)}}{{\left[{\displaystyle \sum_{i=1}^N{\left({Q}_o(i)-\overline{Q_o}\right)}^2}\right]}^{0.5}{\left[{\displaystyle \sum_{i=1}^N{\left({Q}_f(i)-\overline{Q_f}\right)}^2}\right]}^{0.5}}\right\}}^2 $$
(27)
$$ NSE=1-\frac{{\displaystyle \sum_{i=1}^N{\left|{Q}_o(i)-{Q}_f(i)\right|}^j}}{{\displaystyle \sum_{i=1}^N{\left|{Q}_o(i)-\overline{Q_o}\right|}^j}} $$
(28)

where Q o (i) is the i-th observed streamflow; Q f (i) is the i-th forecasted streamflow; and \( \overline{Q_o} \) and \( \overline{Q_f} \) are the average values of observed and computed discharges, respectively.

Fig. 2
figure 2

Streamflow forecasted using entropy spectral analyses for a an upstream station on Iowa River and b a downstream station on Iowa River

Full size image

As shown in Fig. 2, observed monthly streamflow of Iowa River has the largest value in April every year. But it did not monotonically increase or decrease. After a small drop in the month of May, streamflow increases again in June then drops. During the low flow season from September to February, another small peak occurs in October or November. The entropy spectral analyses discussed in this paper, though not exactly, forecasted streamflow of the above characteristics and fitted the observations with r 2 of over 0.5. The forecasted streamflow by RESA was closest to the observations both for upstream and downstream stations, which led to r 2 higher than 0.8.

The peak streamflow of the upstream station in April was correctly forecasted by RESA with less than 2 % error, and by CESA and BESA with errors around 13–17 %. However, the peak time forecasted by BESA and CESA were different. The peak forecasted by BESA was earlier than by CESA, even earlier than the observed value in the 3rd lead year. The earlier peaks forecasted by BESA missed more streamflow volume during the high flow season than the other methods. For the downstream station of Iowa River, the forecast error in streamflow peak by RESA was still within 2 %, but BESA and CESA underestimated the peak by around 19 %.

During the low flow season, the advantage of RESA was significant than the others, where streamflow was forecasted close to the observation, as shown in Fig. 2. However, it is noted that BESA had the poorest forecasting during the low-flow season, compared to the other two methods. The forecasted streamflows in November of the second and third lead years were 4.8 and 3.2 m3/s over the observed value, which is around 1.5 times the observed value. CESA performs between RESA and BESA for forecasting flow in the low flow season.

All three measurements of goodness of fit in Table 2 show that RESA yielded forecasts closest to the observations, and CESA was slightly better than BESA. It seemed that the way of forecasting streamflow using the recursive function of cepstrum analysis had an advantage over linear forecasting used by BESA. The reason is that cepstrum analysis, especially when incorporating prior cepstrum by RESA, helps realize homomorphic characteristics of time series (Oppenheim and Schafer 2004), thus is more applicable than linear forecasting.

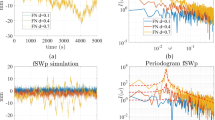
Table 2 Results of forecasting by three entropy spectral analyses
Full size table

The relative errors in forecasts in versus lead time are shown in Fig. 3. As shown in Fig. 3a, RESA generated the smallest errors around 0 and does not change much during the 3 year lead time. However, the relative errors by BESA and CESA tended to get larger as the lead time increased. Larger errors were noticed for forecasting streamflow during the low flow season for BESA and CESA, which is consistent with the previous finding. For the downstream station on Iowa River in Fig. 3b, the relative errors of CESA and RESA were distributed similarly and were closer to 0 than for BESA.

Fig. 3
figure 3

Relative errors by three methods for a an upstream station on Iowa River and b a downstream station on Iowa River

Full size image

4 Conclusions

Three entropy spectral analysis methods, developed from Burg entropy, configurational entropy and relative entropy, are reviewed in the paper. The relative entropy spectral analysis yields the highest resolution in estimating the spectral density of observed streamflow of Iowa River. It shows that the exponential form obtained from either CESA or RESA fit streamflow of Iowa River better than from BESA. The relative entropy spectral analysis also provides the highest reliability in streamflow forecasting. When forecasting lead time increases, RESA is more consistent than the other two methods.