A Novel Forecasting Method Based on F-Transform and Fuzzy Time Series

Abstract

The main goal of time series analysis is to establish forecasting model based on past observations and to reduce forecasting error. To achieve these goals, the present paper proposes a new forecasting algorithm based on the fuzzy transform (F-transform) and the fuzzy logical relationships. First, the F-transform is performed based on partitioning of the universe, and the fuzzy logical relationships are employed to forecast. Two experimental applications are used to illustrate and verify the proposed algorithm. The accuracies are evaluated on the basis of average forecasting error percentage and index of agreement to compare the proposed algorithm with other existing methods.

1 Introduction

One of the main goals of time series analysis is to construct forecasting model that is used to predict future values based on past historical observations. The traditional time series models such as ARIMA and ARCH can not deal with forecasting problems with vague or ambiguous observations represented by linguistic concept. An appropriate way of solving such problem is by the use of time series model based on the fuzzy set theory. In addition, the time series models based on the fuzzy set theory can be applied to small sample data which is not easy to handle in traditional data analysis. To date, many forecasting models based on the fuzzy set theory [45] have been established by many authors and used to reduce forecasting error.

In this paper, we propose a new algorithm to forecast time series which is based on the fuzzy transform (F-transform) and fuzzy logical relationship. The F-transform introduced by Perfilieva [25] has been studied and found useful in many applications in function approximation, image processing [22, 27], numerical solutions of partial differential equations [36], data analysis [29] or neural network approaches [37]. The F-transform converts original data into weighted mean values where the weights are given by the basic functions which are membership functions to identify fuzzy sets. This is a novel method to find an approximation of given data or function.

In a time series analysis and forecast, the use of F-transform and inverse F-transform has been reported in many studies [22, 23, 36,37,38, 41]. In some studies, the F-transform was used to extract a low-frequency trend component [23, 36, 37], whereas it was used for the modeling of an autoregression function in [22]. Also, the inverse F-transform was used as a technical indicator in a stock market instead of the commonly used simple and exponential moving averages in other study [4]. $\hbox {Nov}\acute{a}\hbox {k}$ et al. [23] have used inverse F-transform in combination with perception-based logical deduction, and $\breve{S}\hbox {t}\breve{e}\hbox {pni}\breve{k}\hbox {a}$ et al. [36, 37] have provided forecasts of the future F-transform components.

Song and Chissom [32, 33] firstly introduced fuzzy time series which is a new algorithm of time series forecasting based on fuzzy logic. Many authors have suggested methods to modify and improve the model of Song and Chissom [2, 4, 9,10,11,12,13, 32,33,34,35, 40]. Some authors have applied their models to temperature forecasting [3, 18, 19], and others have used stock index forecasting [9,10,11, 16, 18, 19, 43, 44] to verify their models. Lee and Hong [20] have applied into electric power load forecasting.

Our proposed algorithm using fuzzy transform as defuzzified value of fuzzy sets corresponding to the partitioned intervals of domain is constructed by fuzzy logical relationships based on fuzzy time series. Generally, the fuzzy time series has used the non-overlapped membership functions. However, the proposed fuzzy time series algorithm based on the F-transform allows overlapping membership functions. The weighted sum of defuzzified values based on overlapping membership functions may play an important role in reducing the forecasting error. The proposed algorithm is applied to two well-known data sets: the enrollments of the University of Alabama and the number of patents granted in Taiwan, to show that it is superior to existing methods.

The rest of this paper is structured as follows: In Sect. 2, some preliminary concepts which are required to develop the main results are presented. In Sect. 3, the procedure of a forecasting method based on the F-transform applying fuzzy logical relationship is proposed. In Sect. 4, the experimental applications with enrollment data [32] and patents granted data of Taiwan [21] are provided. Section 5 concludes this study.

2 Preliminaries

A fuzzy subset of ${\mathbb {R}}$ is a map, the so-called membership function, from ${\mathbb {R}}$ into [0, 1]. Thus, a fuzzy subset A is identified by its membership function $\mu _A(x)$. For any $\alpha \in (0,1]$, the crisp set $A_{\alpha }= \{ x \in {\mathbb {R}}: \mu _A(x) \ge \alpha \}$ is called the $\alpha$-cut or $\alpha$-level set of A. The set of all fuzzy numbers will be denoted by ${\mathcal {F}}_c({\mathbb {R}})$. As a special case, we often use the following parametric class of fuzzy numbers, the so-called LR-fuzzy numbers:

$$\begin{aligned} \mu _A(x) = \left\{ \begin{array}{ll} L\left( (m-x)/l\right) &{} \quad \text {if}\quad x\le m, \\ R\left( (x-m)/r\right) &{} \quad \text {if}\quad x>m \\ \end{array} \right. \quad \text{for}\,x \in {\mathbb {R}}, \end{aligned}$$

where $L,R: {\mathbb {R}}^{+} \rightarrow [0,1]$ are fixed left-continuous and non-increasing functions with $R(0) = L(0) = 1$ and $R(1) = L(1) = 0$. L and R are called left and right shape functions of A, m the mode of A and $l, r > 0$ are left, right spread of A. For any fuzzy set A, the function $\mu _A(x) : {\mathbb {R}} \rightarrow [0,1]$ represents the membership function for which $\mu _A(x)$ indicates the degree of membership of $x \in {\mathbb {R}}$ that belongs to the fuzzy set A.

Fuzzy partitions which are needed in F-transform are introduced in several studies [8, 22, 25]. Here, we introduce some basic concepts defined in [25, 26, 28].

Let $c_1< \cdots < c_k$ be fixed nodes within [a, b], such that $c_1 = a, c_k = b$ and $k \ge 2$. We say that fuzzy sets $A_1$, $\ldots$, $A_k$, identified with their membership functions $\mu _{A_1}(x)$, $\ldots$, $\mu _{A_k}(x)$ defined on [a, b], constitute a fuzzy partition of [a, b] if they fulfill the following conditions for $l = 1,\ldots , k$:

• 1. $\mu _{A_l} : [a, b] \rightarrow [0, 1]$, $\mu _{A_l}(c_l) = 1;$

• 2. $\mu _{A_l }(x) = 0$ if $x \not \in (c_{l-1}, c_{l+1})$ where for uniformity of the notation, we put $c_0 = a$ and $c_{k} = b$;

• 3. $\mu _{A_l} (x)$ is continuous;

• 4. For all $x \in [a, b]$,

  $$\sum _{l=1}^{k} \mu _{A_l} (x) >0.$$

  The membership functions $\mu _{A_1},\ldots , \mu _{A_k}$ are called basic functions.

The example of fuzzy sets $A_1, \ldots ,A_k$ with symmetric triangular membership functions on the interval [a, b] is given for $(l = 1, \ldots , k)$ below:

$$\begin{aligned} \mu _{A_l}(x) = {\left\{ \begin{array}{ll} 1-\left| \frac{x-c_l}{h_l} \right| &\quad x \in [c_{l-1}, c_{l+1 }], \\ 0 & \quad \text {otherwise,} \\ \end{array}\right. } \end{aligned}$$

where $h_l =c_{l+1}-c_l$, $c_0 =a$ and $c_{k+1} =b$.

Let a discrete function $f:X\rightarrow {\mathbb {R}}$ be given at a finite set of points $X= \{x_t : t=1 \ldots , n \} \subseteq [a,b]$. The F-transform of a discrete function f with respect to $A_1, \ldots , A_k$ defines the numerical vector $F_k[f]=[F_1, F_2, \ldots , F_k]$, where each $F_l$ is given by

$$F_l=\frac{\sum _{t=1}^{n}f(x_t) \mu _{A_l} (x_t )}{\sum _{t=1}^{n} \mu _{A_l} (x_t)}, \quad l=1, \ldots , k.$$

(1)

The $F_l$ are weighted mean values of f, where the weights are determined by the membership values. The $F_l$ are called components of the discrete F-transform.

Let $F_k[f]=[F_1, \ldots , F_k]$ be the F-transform of f with respect to $A_1, \ldots , A_k$. Then the function

$$f_{F,k}(x_t)=\frac{\sum _{l=1}^{k} \mu _{A_l} (x_t) F_l}{\sum _{l=1}^{k} \mu _{A_l}(x_t)}, \quad t=1, \ldots , n.$$

(2)

is called the inverse F-transform of f. The inverse F-transform $f_{F,k}$ can approximate f with an arbitrary precision. For various properties of the F- transform and detailed proofs, see [28].

Next, we give some definitions of fuzzy time series proposed by Song and Chissom [32,33,34] and present a well-known fuzzy time series algorithm.

Let $y_t (t=\ldots ,0,1,2,\ldots )$, a subset of ${\mathbb {R}}$, be the universe of discourse on which fuzzy sets $A_i (i=1,2, \ldots )$ are defined and let F(t) be a collection of $A_i$. Then, F(t) is called a fuzzy time series on $y_t (t=\cdots ,0,1,2,\ldots )$. If for any time t, $F(t)=F(t-1)$ and F(t) only has finite elements, then F(t) is called a time-invariant fuzzy time series. Otherwise, it is called a time-variant fuzzy time series.

Suppose $F(t-1)=A_i$ and $F(t)=A_j$, a fuzzy logical relationship is defined as $A_i \rightarrow A_j$. Fuzzy logical relationships can be further grouped together into fuzzy logical relationship groups according to the same left-hand sides of the fuzzy logical relationships. For example, there are fuzzy logical relationships: $A_i \rightarrow A_{j1}$, $A_i \rightarrow A_{j2}, \ldots$, and $A_i \rightarrow A_{jk}$. These fuzzy logical relationships can be grouped into a fuzzy logical relationship group as follows: $A_i \rightarrow A_{j1}, A_{j2},\ldots , A_{jk}.$

Song and Chissom employed five main procedures in fuzzy time series as follows: (1) define and partition the universe of discourse; (2) define fuzzy sets and fuzzify the observed data; (3) establish the fuzzy logical relationships; (4) divide the derived fuzzy logical relationships into fuzzy logical relationship groups and forecast; and (5) defuzzify the forecasting results.

3 Fuzzy Time Series Forecasting

It is assumed in this paper that observed time series $\{y_t\}$ is time invariant. In case $\{y_t\}$ is time variant, we transform it to invariant time series applying proper time differences with proper time lags. The prediction procedure is proposed as follows:

• 1. Determine the universe of discourse U. Let $D_{\text {max}}$ and $D_{\text {min}}$ be the maximum and the minimum values of the observed time series data $\{y_t : t=1,2, \ldots , n \}$. Then the universe of discourse U is defined by $[{D_{\text {min}} }-c_1, D_{\text {max}} + c_2]$, where $c_1$ and $c_2$ are the proper positive real numbers for simplifying these end points.

• 2. Partition the universe of discourse U into several subintervals and generate fuzzy sets $\{A_1, A_2, \ldots , A_{k}\}$ forming a fuzzy partition of U. A fuzzy partition for U is constructed by a decomposition $\{a=c_1< c_2< \cdots < c_k=b \}$ of U into $k-1$ subintervals $I_j=[c_j,c_{j+1}],$ $j=1,\ldots , k-1$ and by fuzzy sets $\{A_1, A_2, \ldots , A_{k}\}$ identified by the membership functions (the basic functions) $\mu _{A_1}(x),\ldots , \mu _{A_k}(x)$ for $x \in U$.

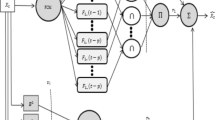
• 3. Fuzzify the observed time series data $\{y_t : t=1,2, \ldots , n \}$. Each of the data is fuzzified q times which is the number of overlapped membership functions of corresponding data. In Fig. 1a, if $y_t$ is included in the subinterval $I_j$ and membership function defined on $I_j$ is a left shape function of $\mu _{A_{j+1}}(x)$, then we obtain $A _{j+1}^{1}$ for its fuzzification. If membership function of defined on $I_j$ is a right shape function of $\mu _{A_{j}}(x)$, then we obtain $A _{j}^{2}$ for its fuzzification. In Fig. 1, the number of overlapped membership functions $q = 2$ in (a), (b) and $q = 3$ in (c) (Fig. 2).

• 4. Calculate $F_1^h, F_2^h, \ldots F_{k}^h$ $(h=1, 2, \ldots , q)$ which are corresponding to $A_1^h, A_2^h$, $\ldots , A_{k}^h$ based on the following formula:

  $$F_j^h=\frac{\sum _{t=1}^{n}y_t \mu _{A_j^h} (y_t )}{\sum _{t=1}^{n} \mu _{A_j^h} (y_t)}, \quad j=1, \ldots , k,$$

  (3)

  where $\mu _{A_j^h} (y_t)$ is the membership degree of $A_j^h$ at $y_t$.

• 5. Construction of fuzzy logical relationships. A fuzzy logical relationship is defined as the transition of the state at time $t-1$ to the state at time t. This is expressed as $A_i^h \rightarrow A_j^h (h = 1, 2, \ldots , p)$, where $A_i^h$ and $A_j^h$ are the states at $t- 1$ and t, respectively.

• 6. Calculate defuzzified predicted value $m_j^h$ for each h at time t. At time t, $m_j^h (h=1,\ldots , p)$ is determined by the following rules:

  • (i) Rule 1:  If the fuzzy logical relationship in the $\lambda$th order FLRGs is defined as

    $$A_{i \lambda }^h, A_{i(\lambda -1)}^h, \ldots , A_{i 2}^h, A_{i1}^h \longrightarrow A_{j}^h$$

    then the value of $m_j^h$ is equal to $F_j^h$ corresponding to $A_j^h$.

  • (ii) Rule 2:  If the fuzzy logical relationship in the FLRGs is shown as

    $$A_{i \lambda }^h, A_{i(\lambda -1)}^h, \ldots , A_{i 2}^h, A_{i1}^h \longrightarrow A_{j1}^h, A_{j2}^h,\ldots , A_{jr}^h(r \ge 2)$$

    then the value of $m_j^h$ is equal to average of $F_{j1}^h, F_{j2}^h, \ldots F_{jr}^h$ corresponding to $A_{j1}^h,A_{j2}^h, \ldots , A_{jr}^h$, respectively. Thus, $m_j^h$ is given by

    $$m_j^h=\frac{1}{r}\sum _{s=1}^{r}F_{js}^h.$$

    (4)

  • (iii) Rule 3:  If the fuzzy logical relationship in the FLRGs is shown as

    $$A_{i \lambda }^h, A_{i(\lambda -1)}^h, \ldots , A_{i 2}^h, A_{i1}^h \longrightarrow \text {empty}$$

    (5)

    then the value of $m_j^h$ is

    $$m_j^h=\frac{\lambda F_{i1}^h+(\lambda -1)F_{i2}^h +\cdots +1 F_{i \lambda }^h}{\lambda +(\lambda -1)+\cdots +1}.$$

    (6)

• 7. Calculate the forecasted value $m_j$ at time t as follows:

  $$m_j= \frac{\sum _{h=1}^{p}w_j^h m_j^h}{\sum _{h=1}^{p} w_j^h},$$

  (7)

  where $w_j^h= \frac{\lambda \mu _{A_{i1}^h}(y_t)+(\lambda -1) \mu _{A_{i2}^h}(y_t)+\cdots + \mu _{A_{i \lambda }^h}(y_t)}{\lambda +(\lambda -1)+\cdots +1}$ is the weighted value of $m_j^h$ with respect to its membership degree.

Based on the seven steps presented above, the estimator for time series prediction can be obtained using F-transform.

Fig. 1

Examples of basic functions. a Triangular function, b sinusoidal function, c trapezoidal function

Fig. 2

Comparison of the predicted value and the actual value

The accuracy of the forecast can be evaluated by the basis of the index of $\hbox {agreement}\,(D_1)$ and the basis of the index of $\hbox {agreement}\,(D_2)$ suggested by Willmott [42]. These are computed as follows:

$$D_1(\%)= \frac{1}{N}\sum _{i=1}^{N}\bigg |\frac{P_i -O_i}{O_i} \bigg |\times 100,$$

(8)

$$D_2= 1-\left[ \frac{\varSigma (P_i-O_i)^2}{\varSigma (|P_i-\bar{O}|+|O_i-\bar{O}|)^2}\right] ,\quad 0 \le D_2 \le 1,$$

(9)

where N is the total number of data and $O_i$, and $P_i$ are the observed and predicted loads, respectively. $O_i$ is the mean value of the observed value. The metric $D_2$ quantifies the relative contribution of systematic error to random error and has a value of 1 in a perfect model [42].

4 Applications

In this section, we compare the accuracies of the fuzzy time series predictions by the method using F-transform provided in Sect. 3 on two data sets which are frequently used in fuzzy time series analysis.

4.1 Enrollment Data

The enrollment of the University of Alabama was introduced by Song and Chissom [32]. Many authors have used this data set which is provided in Table 1 to compare their works with other methods [5,6,7, 14, 24, 30, 31, 39]. Before we apply the whole procedure, we transform the data to time-invariant data using difference. The enrollment data from 1971 to 1992 are used as training data set to forecast the enrollment from 1993 to 2006 as follows:

Table 1 Results of training set using $1\text{st}$ order FLR

• 1. Define the universe of discourse U as $[{D_{\text {min}} }-c_1, D_{\text {max}} + c_2]$ = $[-1000,1400]$, where $D_{\text {min}}=-955$ and $D_{\text {max}}=1291$ with proper constants $c_1$ and $c_2$.

• 2. Partition U into 8 intervals $I_j=[c_j, c_{j+1}]$ where $c_1=-1000$ and $c_{j+1}=-1000+300j$ $(j=1,\ldots ,8)$. Construct a fuzzy partition of an interval by fuzzy sets with symmetric triangular basic functions as follows: $A_1 =[-1000, -700]$, $A_2 =[-1000, -400]$, $A_3 =[-700, -100]$, $A_4 =[-400, 200]$, $A_5 =[-100, 500]$, $A_6 =[200, 800]$, $A_7 =[500, 1100]$, $A_8 =[800, 1400]$, $A_9 =[1000, 1400]$.

• 3. There are two triangular membership functions for each $y_t$; $y_t$ can be fuzzified into two different types. For example, at $t=1972$, 508 has corresponding membership degree 0.027 of fuzzy set $A_7=[500,1100]$; it is fuzzified into $A_7^1$. At the same time, 508 has corresponding membership degree 0.973 of fuzzy set $A_6=[200,800]$; it is fuzzified into $A_6^2$. Similarly, at $t=1973$, 304 has corresponding membership degree 0.347 of fuzzy set $A_6=[200,800]$; it is fuzzified into $A_6^1$. At the same time, 304 has corresponding membership degree 0.653 of fuzzy set $A_5$; it is fuzzified into $A_5^2$.

• 4. From (3), Table 2 shows $F_1^h, \ldots , F_9^h$ $(h=1,2)$ which are corresponding to fuzzy sets $(A_1^h, \ldots , A_9^h)$. All values are rounded off to three decimal places.

Table 2 Defuzzified values $F_j^h$ of fuzzy sets $A_j^h$

• 5. Table 3 shows 1st order fuzzy logical relationship obtained from given fuzzy time series.

Table 3 Fuzzy logical relationships of first order

• 6. From Table 3, defuzzified values of predicted can be obtained. For example, left and right FLRs at $t=1973$ are $A_7^1 \rightarrow \{ A_6^1, A_4^1\}$, $A_6^2 \rightarrow \{ A_5^2, A_3^2\}$, respectively. By Rule 2, defuzzified values of predicted fuzzy numbers are:

  $$m_{1973}^1=\frac{1}{2}\left( F_4^1 +F_6^1\right) =66.98, m_{1973}^2=\frac{1}{2}\left( F_3^2 +F_5^2\right) =-11.26$$

  At $t=1983$, left and right FLRs are $A_2^1 \rightarrow \{ A_5^1\}$, $A_1^2 \rightarrow \{ A_4^2\}$. By Rule 1, defuzzified values of predicted fuzzy numbers are:

  $$m_{1983}^1=F_5^1 =61.93, m_{1983}^2=F_4^2=39.46$$

• 7. Forecasted values can be obtained as follows: For example, for $1972 \rightarrow 1973$, the weight of 1th order FLR is $w_{1973}^h=\mu _{A_{l}^h(508)}$. So, we get $w_{1973}^1=0.027$, $w_{1973}^2=0.973$. Hence, the forecasted value at $t=1973$ is

  $$m_{1983}=\frac{0.027*66.98+0.973*(-11.26)}{0.027+0.973}+13{,}452=13{,}553.83.$$

  Similarly, when $1982 \rightarrow 1983$, $w_{1983}^1=0.150$, $w_{1983}^2=0.850$ are the weights. Hence, the forecasted value at $t=1983$ is

  $$m_{1983}=\frac{0.150*61.93+0.850*39.46}{0.150+0.850}+15{,}433=15{,}475.83.$$

For training set, we have used the data from 1971 to 1992. Table 3 shows 1st order FLR, and Table 4 shows the accuracies of the results. As it is shown in Table 5, generally higher order may improve the accuracy, but it may cause difficulties to find the forecasting value because of its complexity. Table 6 provides comparison with many method suggested by many authors such as Chen et al. [5].

Table 4 Results of training set using 1th order FLR

From the FLR of the training set in Table 3, the corresponding fuzzy set of $t=1992$ are $t=1992$ are $A_3^1$, $A_2^2$. So we obtain $m_{1993}^1=61.93$, $m_{1993}^2=39.46$, and $w_{1993}^1=0.797$, $w_{1993}^2=0.203$ at $t=1993$. So, the 1th order forecasted value at $t=1993$ can be represented by

$$m_{1993}=\frac{0.797*61.93+0.203*39.46}{0.797+0.203}+18{,}876=18{,}933.36.$$

Table 5 Forecasting results of high order

Table 6 The forecasting results of different forecasting methods

Forecasted value $(m_{1994})$ of $t=1994$ can be obtained after we add one more data item $(m_{1993})$ of $t=1993$ to the training data set. Table 7 shows the forecasted values from 1993 to 2006.

Table 7 Forecasted values and accuracies

4.2 The Number of Patents Granted in Taiwan

Table 8 shows the number of patents granted in Taiwan from 1980 to 2000 introduced by Liu [21]. The data set is transformed to be invariant time series by using first-order time difference because it is increasing. $[-7000, 11,000]$ is chosen to be the universe discourse based on minimum value $-6017$ and maximum value 10675. Here, we have used triangular fuzzy numbers for basic functions on 9 $\hbox {intervals}\,(q = 9)$. Forecasted data are provided in Table 8 with original data. Table 9 shows the accuracies after performing all 7 steps based on the orders of transform through time differences. 2nd order is chosen to forecast the data. Comparisons of the proposed method with other existing methods are provided in Table 10.

Table 8 Patents granted data and forecasted values

Table 9 Forecasting accuracies of patents granted data of Taiwan

Next, we perform validations to confirm the superiority of the proposed method. The data from 1980 to 1995 have been used for training data set, and from 1996 to 2000 for testing data. The data from 1980 to 1995 are used to forecast the data at $t=1996$. For forecasting the data at $t=1997$, we add the data at $t=1996$ to training data set. Likewise, we update the training data set adding one data point for the next forecasting. The forecasted results and the accuracies are provided in Table 11, which shows very good performances with $D_1=2.8826$ and $D_2=0.9882$.

Table 10 Comparison of accuracies of various forecasting methods

Table 11 Forecasted values and accuracies of high orders of patents granted data

5 Conclusions

In this paper, we propose a novel forecasting method based on F-transform and fuzzy time series to improve the forecasting accuracy. After applying F-transform to observed data, we construct a new fuzzy time series algorithm based on fuzzy logical relationships and F-transformed data. Through the real applications to enrollments of the University of Alabama and the number of patents granted in Taiwan, we show that forecasting accuracy can be further enhanced thorough applying F-transform. In addition, it is confirmed from these applications that the proposed method has better forecasting performances than existing methods. Future work involves extending the proposed method to handle two-factors fuzzy time series model and giving some results using various real applications to prove that it is correct.