1 Introduction

Biometrics and face recognition, in particular, have been one of the most intensively explored computer vision areas in the computer science community. It is motivated by a vast area of applications in border checking, surveillance systems, mobile devices, passport and driver’s license verification, etc. A choice of the biometrics method can depend upon an application, hardware, memory resources, time constraints and other factors. Modern approaches based on deep learning [17], sparse representation [46] or multimodal biometrics [20] led to good results. Classic methods such as principal component analysis (PCA [43]), linear discriminant analysis (LDA [6]), local descriptors [1] and others are still being enhanced. Moreover, there exist hybrid constructs such as the proposed in [48] or the proposals incorporating experts [23].

The strategies which save memory resources and potentially improve the accuracy of recognition processes are aggregation techniques. They can be divided into a few relatively similar groups, namely aggregations of classifiers based on particular non-overlapping facial regions where the final classification is a result of combining the specific results. In case of overlapping areas, we may talk information fusion. The next group is constituted by the multimodal biometrics. Slightly different class of methods are the approaches based on aggregation of information at the data level. A vast plethora of applications of fuzzy logic, e.g., [5, 30, 41] offers an attractive possibility of using fuzzy measure-based constructs to aggregate the classification results.

Let us briefly recollect some essential results reported in the literature. In [8], eyes, nose, mouth and the whole face scores are added when template matching strategy is applied producing significant improvement in recognition result. Again, a few aggregation proposals for the eigenfaces method for the selected facial areas are presented in [40]. Classifiers based on the RBF neural networks are fused through the majority rule in [15]. In [19], majority voting and Bayesian product are used to aggregate chosen methods of dimensionality reduction. The work [28] at the decision level suggests the weighted sum rule for fusion of similarity matrices. Utility functions serve as aggregation operators [12]. Three-valued and fuzzy set-based decision mechanisms are proposed as aggregation techniques in multimodal biometrics [2]. Finally, fuzzy measure and fuzzy integral find their applications in many facial and pattern recognition studies as an efficient aggregation techniques, namely [21, 24,25,26, 31,32,33,34,35,36,37,38]. Additionally, an interesting comparison of triangular norms in terms of their statistical non-distinguishability was present in [16].

Aggregation functions are widely studied because of their applications, mainly in decision-making theory, see [14]. They, in general, should satisfy the condition of monotonicity and special boundary conditions (see next section). We are interested in a generalization of Choquet integral in the context of introduction of some kind of structural flexibility by applying t-norms instead of product under the integral sign. In [9, 29], this weaker class of functions (when compared to the aggregation conditions) was introduced and called pre-aggregation functions. They are monotonic along a fixed direction which is called directional monotonicity.

The main goal of this study is to apply this broad class of functions to the problem of face recognition and, to compare their efficiency as the aggregation vehicle, to the initial Choquet integral operator which is one of the commonly encountered aggregation functions, which was proved in above-mentioned works. In particular, we are interested in building twenty-five classes of this kind of integral which are constructed on the basis of an application of t-norms instead of product under the integral sign. Using four well-known face recognition datasets: FERET [44], AT&T [4], Yale Face Database [47] and cropped version [45] of the Labeled Faces in the Wild [18], we compare the performance of the generalized Choquet integrals in an application to the methods such as PCA, LDA, LBP [1], multiscale block LBP [10, 27], chain code-based local descriptor (CCBLD, [22]) and full ranking [11] when applied to various facial part images and/or the images of the whole face.

The paper is organized as follows. The general properties of aggregation functions and the role of the fuzzy measure and Choquet integral in the process of face recognition are covered in Sect. 2. Section 3 discusses the experimental results while Sect. 4 presents conclusions and directions for the future studies.

2 Aggregation Functions and a General Processing Scheme

Let us recall the basic definitions and properties of pre-aggregation functions.

Definition 1

([7]) We say \(f:[0,\,1]^n\rightarrow [0,\,1]\) is an aggregation function if it satisfies the following conditions: (i) If \(x_i\le x,\) then \(f\left( x_1,\ldots ,x_{i-1},x_i,x_{i+1},\ldots ,x_n\right) \le f\left( x_1,\ldots ,x_{i-1},x,x_{i+1},\ldots ,x_n\right)\) for each \(x_i, i=1,\ldots ,n\); (ii) \(f\left( 0,\ldots ,0\right) = 0\); (iii) \(f\left( 1,\ldots ,1\right) = 1\).

Definition 2

([29]) A function \(f:[0,\,1]^n\rightarrow [0,\,1]\) is said to be \({\mathbf {r}}\)-increasing if for all points \((x_1,\ldots ,\ldots ,x_n)\) and for all \(c>0\)

$$\begin{aligned}{l} f\left( x_1,\ldots ,x_n\right) \le\, f\left( x_1+cr_1,\ldots ,x_n+cr_n\right), \hbox{ where } {\mathbf {r}}=\left( r_1,\ldots ,r_n\right) . \end{aligned}$$

Now, we recall the concepts of \(\lambda\)-fuzzy measure and Choquet integral. Since in this study we explore them in the context of face recognition, we use the terminology coming from this application domain.

Definition 3

([39]) Let \(X=\{x_1,\ldots ,x_n\}\) denote the whole face with \(x_1,\ldots ,\,x_n\) being the particular facial areas such as eyes, eyebrows, mouth. A set function \(g:P(X)\rightarrow [0,1]\) is called a fuzzy measure if it satisfies the following properties: (i) \(g(\emptyset )=0\); (ii) \(g(X)=1\); (iii) \(g(A)\le g(B)\) for \(A \subset B\), where \(A,B\in P(X)\).

If A and B are disjoint sets, \(\lambda\)-fuzzy measure [42] is a fuzzy measure that fulfills the following rule: \(g(A \cup B)=g(A)+g(B)+ \lambda g(A)g(B),\, \lambda >-1.\) The parameter \(\lambda \ne 0\) can be uniquely determined based on the following equality [42] \(1+ \lambda =\prod \nolimits _{i=1}^n(1+\lambda g_i),\) where \(g_i=g(\{x_i \})\) are fixed. Using the notation \(A_i=\{x_1,\ldots ,x_i \},\, A_{i+1}=\{x_1,\ldots ,x_i,x_{i+1} \}\) for overlapping facial areas, one can write the recursive relation \(g(A_{i+1} )=g(A_i )+g_{i+1}+ \lambda g(A_i ) g_{i+1},\) where \(g(A_1 )=g_1.\)

Definition 4

([39]) Using the above notation, Choquet integral is defined as follows

$$\begin{aligned} {\text {Ch}}\int h\circ g=\sum \limits _{i=1}^n\left( h\left( x_i \right) -h\left( x_{i+1} \right) \right) g\left( A_i \right) , \end{aligned}$$
(1)

where the function \(h:X\rightarrow \left[ 0,1\right]\) and \(h\left( x_{n+1}\right) =0\). Its values are reordered in a non-decreasing order so that \(h\left( x_i \right) \ge h\left( x_{i+1} \right) ,\, i=1,\ldots ,n.\)

Remark 1

In the experimental part, the following notation [26] is applied: \(h\left( y_{ik} \right) =\frac{1}{N_k} \sum \nolimits _{\mu _{ij}\in C_k} \mu _{ij}\) where \(N_k\) stands for a number of images in k-th class \(C_k\), and the membership grades \(\mu _{ij}\) are given by \(\mu _{ij}=\frac{1}{1+\frac{d_{ij}}{\bar{d_i}}}\). Here i is a classifier number, j is the training image index, \(\bar{d_i}\) is the average distance within ith classifier, and finally, \(d_{ij}\) means a distance between a given testing image and jth facial image within ith classifier.

Theorem 1

([29]) Let \(M : [0, 1]^2 \rightarrow [0, 1]\) satisfy \(M(x, y) \le x,\, M(x, 1) = x,\, M(0, y) = 0\) and let M be (1, 0)-increasing. Finally, let, for any fuzzy measure g, a generalized Choquet integral be a function of the form

$$\begin{aligned} Ch' \int h\circ g(M)=\sum \limits _{i=1}^nM\left( \left( h\left( x_i \right) -h\left( x_{i+1} \right) \right) , g(A_i)\right) , \end{aligned}$$
(2)

where \(h\left( x_{n+1}\right) =0.\) Then, there exists such a nonzero vector \({\mathbf {r}}\) that \(Ch'\) is \({\mathbf {r}}\)-increasing and it satisfies the conditions: \(f\left( 0,\ldots ,0\right) = 0, f\left( 1,\ldots ,1\right) = 1,\) and \(\min \left( x_1, \ldots , x_n\right) \le Ch' \le \max \left( x_1, \ldots , x_n\right).\)

This theorem suggests a potential applicability of the function (2) as a suitable aggregation operator, particularly in the decision-making problems. Hence, we discuss here a large collection of t-norm families which can be applied as the function \(M\left( x,y\right)\) [see formula (2)]. As the reference, we have used the monograph [3, p. 72, Table 2.6] and paper [29] where simple functions as minimum \(T_{M}\left( x,y\right) =\min \left( x,y\right)\), product \(T_{P}\left( x,y\right) =xy\), Łukasiewicz t-norm \(T_{L}\left( x,y\right) =\max \left( 0,x+y-1\right)\), drastic product \(T_{D}\left( x,y\right) =y\) or x or 0 for \(x=1\), \(y=1\), or \(x,\, y\ne 1\), respectively, nilpotent minimum \(T_{NM}\left( x,y\right) =\min \left( x,y\right)\) for \(x+y>1\) or 0 otherwise, and Hamacher product \(T_H\left( x,y\right) =xy/\left( x+y-xy\right)\) for \(x,y\ne 0\) and 0 otherwise were considered. For instance, the first family of the t-norms present in [3] is \(T_\alpha \left( x,y\right) =\left( \max \left[ x^{-\alpha }+y^{-\alpha }-1,0\right] \right) ^{-\frac{1}{\alpha }},\, \alpha \in \left( -\infty ,0\right) \cup \left( 0,\infty \right) .\) The range of a value of parameter \(\alpha\) may depend upon a choice of t-norm.

Example 1

Let us consider the reference data coming from [39]. Namely, let \(g_1=0.6,\,g_2 = 0.35,\,g_3 = 0.05,\,g_4 = 0.21,\, g_5 = 0.72\) and \(h_1=0.1,\, h_2 = 0.4,\, h_3 = 0.3,\, h_4 = 0.7,\, h_5 = 0.05\). Then, \({\text {Ch'}}\int h\circ g\left( T_P\right) \approx 0.31\), \({\text {Ch'}}\int h\circ g\left( T_M\right) \approx 0.61\), \({\text {Ch'}}\int h\circ g\left( T_L\right) \approx 0.05\), \({\text {Ch'}}\int h\circ g\left( T_D\right) \approx 0.31\), \({\text {Ch'}}\int h\circ g\left( T_{NM}\right) \approx 0.05,\) and \({\text {Ch'}}\int h\circ g\left( T_H\right) \approx 0.5\).

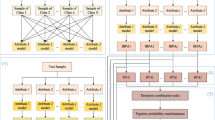
Now, let us present a general processing scheme. First, a face image is partitioned onto subimages corresponding to specific facial parts or this facial image (a whole face) is treated by a few transformation algorithms. Each of the algorithms or feature-based classifiers produces the distances between the testing image and training images, of course in a new feature space such as, for instance, new vectors generated by PCA transform corresponding to particular images. The distances obtained in the classification processes form an input to the Choquet integral with an assumption that the values \(h\left( \cdot \right)\) are defined as mentioned in Remark 1. The final decision about the belongingness to a particular class is made on the basis of the values of the Choquet integral. The highest value is suspected to point at the sought class, see Fig. 1. It is worth noting here that the function \(M\left( \cdot ,\cdot \right)\) appearing in (2) is replaced by any two-argument t-norm.

Fig. 1
figure 1

An overall processing scheme

Full size image

3 Experimental Studies

In the first series of experiments, we used the AT&T set of facial images. The faces were initially cropped and scaled. Next, we asked 18 people (members of our lab or friends) to provide the weights of saliency of six chosen facial parts considered in the processes of human or computer face recognition. According to their answers, we obtained the average weights shown in Table 1. Examples of related facial regions taken from the AT&T and FERET gray-scale subset (after scaling, cropping the face, and histogram equalization) are depicted in Fig. 2. Next, we conducted a series of 100 classification processes for the well-known methods such as PCA (separately, for the two norms serving as distances between vectors representing facial features after the image transformation, which are the Euclidean and Canberra distances). In each series of experiments, five images of each person were randomly selected to the training set and the rest five to the testing set. In Table 2, listed are the values of parameter \(\alpha\) for corresponding t-norm families for which the average classification results were higher than for the classic Choquet integral with product t-norm. Moreover, the maximal difference and its corresponding argument are presented. It is worth to stress here that the obtained values of classification are not important in this comparison, since the Choquet integral has demonstrated to be one of the best aggregation operators used in face recognition, see, for instance [26]. Hence, only the positive differences are discussed to find an alternative operator, if any. Additionally, two functions which can be considered as aggregation operators, namely median and voting (denoted in the resulting tables as m and v, respectively), were compared. Similar statistics are presented in Table 3, where LDA method with three norms (Euclidean, cosine and Canberra) was incorporated. Tables 4 and 5 present the analogous results for six local descriptors: LBP, MBLBP with 3, 5 and 7 pixel width block sizes, full ranking and CCBLD, respectively. The descriptors here were used in their simplest forms without division of the images into subregions. Relatively similar tests were conducted for the FERET database. In 100 repetitions, two images were randomly selected to the training and one image was chosen to the testing set, respectively. The results for selected three norms, namely Euclidean, cosine and correlation, are listed (see Table 6). Finally, a series of experiments for Yale dataset, where all above-mentioned local descriptors were compared with their best settings for the whole images, is established. Five images of each person were randomly selected to constitute the training set in each of the 100 repetitions. Eight methods (PCA and LDA with Euclidean norm) and six local descriptors were tested for the PCA whole faces with the same protocol as previously. Finally, the LFW dataset was checked for CCBLD, full ranking, MBLBP with 5 px width blocks and simple LBP. The images of people having six photographs were selected. Four of the images were randomly selected to the training set and one was selected to the testing set. The weights needed to construct the Choquet integral were initially obtained in the pretests for each of the classifiers separately. The three last sets of test results are gathered in Table 7. It is worth noting that we checked all the 25 functions with the parameter \(\alpha\) not lower than \(-10\) and not higher than 10 by considering the successive values \(-10,\, -9.9,\,\ldots ,\, 9.9,\,10,\) assuming that such range for the parameter represents a satisfactory level of covering of its values. The results gathered in Tables 2, 3, 4, 5, 6 and 7 show the potential value of a few familes of functions, namely 1st, 3rd, 4th, 5th, 6th, 9th, 10th, 11th, 14th, 15th, 20th and 25th (their indexes correspond to the indexes introduced in [3, p. 72, Table 2.6]) function as the aggregation operator. Moreover, the median and voting functions show that can be substitutes of Choquet integral. However, Table 8 shows the finding which can be relatively surprising in this context. Namely, only the function no. 10, i.e.,

$$\begin{aligned} T_\alpha \left( x,y\right) =\frac{xy}{\left[ 1+\left( 1-x^\alpha \right) \left( 1-y^\alpha \right) \right] ^{\frac{1}{\alpha }}},\, \alpha \in \left( 0,\infty \right) , \end{aligned}$$
(3)

for \(\alpha >3.1\) and median give slightly higher recognition rates when the averages of all 17 considered test cases are taken into consideration. This means that the functions produced the best accuracy rates when substituted into (2) in the place of the function \(M\left( \cdot ,\cdot \right) .\) For each method (classifier), the interval for which a given aggregating function gives the best results varies. Therefore, it is difficult to explicitly predict its value. Even median does not produce the results totally outclassing the rest of functions. On the other hand, the functions no. 16, 19 and 22 have not appeared in any tables; namely, they have never hit the results produced by the classic Choquet integral.

Table 1 Average weights of facial parts
Full size table
Fig. 2
figure 2

Facial regions selected from the AT&T (left) and FERET (right) images, for details, see [24]

Full size image
Table 2 AT&T PCA
Full size table
Table 3 LDA (AT&T)
Full size table
Table 4 Local descriptors (AT&T)
Full size table
Table 5 Local descriptors 2 (AT&T)
Full size table
Table 6 LDA (FERET)
Full size table
Table 7 Various techniques
Full size table
Table 8 Average results
Full size table

4 Conclusions and Future Work

In the study, we have investigated 25 families of well-known t-norms which can replace the product used in the definition of Choquet integral serving as the aggregation operator for the classifiers in face recognition. The classifiers used various facial parts such as eyebrows, eyes, nose, mouth, left and right cheek or the methods such as principal component analysis, linear discriminant analysis, local descriptors based on binary or string words. We selected a single family of functions (3) which can potentially replace the product. Moreover, a collected set of data can serve as the initial values of parameters for the functions considered as potential aggregation operators. The future work can be an application of optimization methods to find the proper parameter value, an application of generalized Choquet integrals to other than face recognition classification problems, and improvement in other fuzzy integrals such as Sugeno or Shilkret [13]. Furthermore, a problem of optimal choice of classifiers taking part in the aggregation process is still open; for instance, the question about the number of facial parts and their saliency in relation to the kind of aggregation operator has not been fully addressed in the literature of the area.