Robust Fuzzy Filter Design for Nonlinear Parabolic Partial Differential Systems with Continuous Wiener Noise and Discontinuous Poisson Noise

Abstract

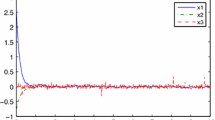
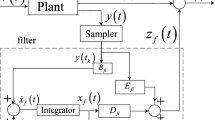
This paper addresses a robust $H_{\infty }$ fuzzy filter design problem for nonlinear stochastic partial differential systems (NSPDSs) with continuous random fluctuation, discontinuous Poisson jumping noise, random external disturbance and measurement noise in the spatiotemporal domain. For NSPDSs, the robust $H_{\infty }$ filter design problem through a measurement output needs to solve a complex second-order Hamilton Jacobi integral inequality. In order to simplify the design procedure, a fuzzy stochastic partial differential system based on a fuzzy interpolation approach is proposed to approximate the NSPDS. Then, the robust $H_{\infty }$ fuzzy filter design problem can be reformulated as a diffusion matrix inequality (DMI) problem. Since the DMI problem is difficult to be solved via traditional algebraic techniques, we utilize the divergence theorem and Poincare inequality to transform the DMIs to a set of linear matrix inequalities (LMIs) which could be easily solved with the help of MATLAB LMI Toolbox. Finally, a robust state estimation problem of an ecology system with intrinsic spatiotemporal continuous Wiener noise and discontinuous Poisson jump fluctuation is provided as an example to illustrate the design procedure and to confirm the $H_{\infty }$ filtering performance of the proposed $H_{\infty }$ fuzzy filter design method.

Appendices

Appendix A: Proof of Theorem 1

Let us choose a positive definition functional $V\left( {\overline{y}}\left( x,t\right) \right) \in C^{2}\left( {\mathbb {R}} ^{n}\right) >0$, $\forall {\overline{y}}\left( x,t\right) \ne 0$, and $V\left( 0\right) =0$. First, we discuss the augmented PDSs in (8) with ${\overline{v}}\left( x,t\right) \ne 0$. By the Itô-Lévy formula in (3), we have

$$\begin{aligned} &E\left\{ \int _{U}\int _{0}^{t_{f}}\left\| e\left( x,t\right) \right\| ^{2}{\text {d}}t{\text {d}}x\right\}&= E\int _{U}\int _{0}^{t_{f}}\left\| e\left( x,t\right) \right\| ^{2}+\frac{\partial V\left( {\overline{y}}\left( x,t\right) \right) }{\partial t}{\text {d}}t{\text {d}}x \nonumber \\&\quad+E\left\{ \int _{U}V\left( {\overline{y}}_{0}\left( x\right) \right) {\text {d}}x\right\} \nonumber \\&-E\left\{ \int _{U}V\left( {\overline{y}}\left( x,t_{f}\right) \right) {\text {d}}x\right\} \nonumber \\& \le E\left\{ \int _{U}V\left( {\overline{y}}_{0}\left( x\right) \right) {\text {d}}x\right\} \nonumber \\&\quad+E\int _{U}\int _{0}^{t_{f}}{\overline{y}}^{\mathrm{T}}\left( x,t\right) Q^{\mathrm{T}}Q\overline{y }\left( x,t\right) \nonumber \\&+\left( \frac{\partial V\left( {\overline{y}}\left( x,t\right) \right) }{\partial {\overline{y}}}\right) ^{\mathrm{T}}\times {\overline{D}} \nabla ^{2}{\overline{y}}\left( x,t\right) \nonumber \\&\quad+\left( \frac{\partial V\left( {\overline{y}}\left( x,t\right) \right) }{ \partial {\overline{y}}}\right) ^{\mathrm{T}}F\left( {\overline{y}}\left( x,t\right) \right) \nonumber \\&\quad+\left( \frac{\partial V\left( {\overline{y}}\left( x,t\right) \right) }{\partial {\overline{y}}}\right) ^{\mathrm{T}}{\overline{G}}_{v}{\overline{v}}\left( x,t\right) \nonumber \\&\quad+\frac{1}{2}F_{W}^{\mathrm{T}}\left( y\left( x,t\right) \right) \times \frac{\partial V^{2}\left( {\overline{y}}\left( x,t\right) \right) }{\partial {\overline{y}}^{2} }F_{W}\left( y\left( x,t\right) \right) \nonumber \\&+\lambda \left[ V\left( {\overline{y}}\left( x,t\right) +T\left( y\left( x,t\right) \right) \right) -V\left( {\overline{y}}\left( x,t\right) \right) \right] {\text {d}}t{\text {d}}x \end{aligned}$$

(A1)

According to Lemma 2 with $X=\left( \frac{\partial V\left( {\overline{y}} \left( x,t\right) \right) }{\partial {\overline{y}}}\right) ^{\mathrm{T}}{\overline{G}} _{v}$ and $Y={\overline{v}}\left( x,t\right)$, the inequality in (A1) can be rewritten as follows:

$$\begin{aligned} E\left\{ \int _{U}\int _{0}^{t_{f}}\left\| e\left( x,t\right) \right\| ^{2}{\text {d}}t{\text {d}}x\right\}& \le E\left\{ \int _{U}V\left( {\overline{y}}_{0}\left( x\right) \right) {\text {d}}x\right\} \nonumber \\&+E\int _{U}\int _{0}^{t_{f}}{\overline{y}}^{\mathrm{T}}\left( x,t\right) Q^{\mathrm{T}}Q{\overline{y}}\left( x,t\right) \nonumber \\&+\left( \frac{\partial V\left( {\overline{y}}\left( x,t\right) \right) }{\partial {\overline{y}}}\right) ^{\mathrm{T}} {\overline{D}} \nabla ^{2}{\overline{y}}\left( x,t\right) \nonumber \\&+\left( \frac{\partial V\left( {\overline{y}}\left( x,t\right) \right) }{ \partial {\overline{y}}}\right) ^{\mathrm{T}}F\left( {\overline{y}}\left( x,t\right) \right) \nonumber \\&+\frac{1}{4\gamma }\left( \frac{\partial V\left( {\overline{y}}\left( x,t\right) \right) }{\partial {\overline{y}}}\right) ^{\mathrm{T}}{\overline{G}}_{v} {\overline{G}}_{v}^{\mathrm{T}}\left( \frac{\partial V\left( {\overline{y}}\left( x,t\right) \right) }{\partial {\overline{y}}}\right) \nonumber \\&+\gamma {\overline{v}}^{\mathrm{T}}\left( x,t\right) {\overline{v}}\left( x,t\right) + \frac{1}{2}F_{W}^{\mathrm{T}}\left( y\left( x,t\right) \right) \nonumber \\&\frac{\partial V^{2}\left( {\overline{y}}\left( x,t\right) \right) }{\partial {\overline{y}}^{2} }F_{W}\left( y\left( x,t\right) \right) \nonumber \\&\lambda \left[ V\left( {\overline{y}}\left( x,t\right) +T\left( y\left( x,t\right) \right) \right) -V\left( {\overline{y}}\left( x,t\right) \right) \right] {\text {d}}t{\text {d}}x \end{aligned}$$

(A2)

If the following HJII holds

$$\begin{aligned} \begin{array}{l} \int _{U}{\overline{y}}^{\mathrm{T}}\left( x,t\right) Q^{\mathrm{T}}Q{\overline{y}}\left( x,t\right) +\left( \frac{\partial V\left( {\overline{y}}\left( x,t\right) \right) }{\partial {\overline{y}}}\right) ^{\mathrm{T}}F\left( {\overline{y}}\left( x,t\right) \right) \ \\ \quad +\left( \frac{\partial V\left( {\overline{y}}\left( x,t\right) \right) }{ \partial {\overline{y}}}\right) ^{\mathrm{T}}{\overline{D}}\nabla ^{2}{\overline{y}}\left( x,t\right) \\ \quad +\frac{1}{2}F_{W}^{\mathrm{T}}\left( y\left( x,t\right) \right) \frac{\partial V^{2}\left( {\overline{y}}\left( x,t\right) \right) }{\partial {\overline{y}}^{2} }F_{W}\left( y\left( x,t\right) \right) \\ \quad +\frac{1}{4\gamma }\left( \frac{\partial V\left( {\overline{y}}\left( x,t\right) \right) }{\partial {\overline{y}}}\right) ^{\mathrm{T}}{\overline{G}} _{v}\times {\overline{G}}_{v}^{\mathrm{T}}\left( \frac{\partial V\left( {\overline{y}} \left( x,t\right) \right) }{\partial {\overline{y}}}\right) \\ \quad +\lambda \left[ V\left( {\overline{y}}\left( x,t\right) +T\left( y\left( x,t\right) \right) \right) -V\left( {\overline{y}}\left( x,t\right) \right) \right] {\text {d}}x<0 \end{array} \end{aligned}$$

(A3)

i.e., the inequality (11) holds, then the robust $H_{\infty }$ filter performance on the spatiotemporal domain U achieves to (10) if the initial state $V\left( {\overline{y}}_{0}\left( x\right) \right) \ne 0$, or the robust $H_{\infty }$ filter performance achieves to (9) if the initial state $V\left( {\overline{y}}_{0}\left( x\right) \right) =0$.

In the case ${\overline{v}}\left( x,t\right) =0$, for all $x\in U$ and $t\in \left[ 0,\infty \right)$. Then, (10) becomes

$$\begin{aligned} E\left\{ \int _{U}\int _{0}^{t_{f}}\left\| e\left( x,t\right) \right\| ^{2}{\text {d}}t{\text {d}}x\right\} \le E\left\{ \int _{U}V\left( {\overline{y}}_{0}\left( x\right) \right) {\text {d}}x\right\} \end{aligned}$$

(A4)

Since the right-hand side of (A4) is a finite value dependent on the bounded initial state ${\overline{y}}_{0}\left( x\right)$ and the compact set U. Then, $\left\| e\left( x,t\right) \right\| ^{2}\rightarrow 0$ as $t_{f}\rightarrow \infty$, $\forall x\in U$; i.e., the filtering error system without external disturbance ${\overline{v}}\left( x,t\right)$ in (8) is asymptotically zero in the mean square sense. We finish the proof of Theorem 1. $\square$

Appendix B: Proof of Theorem 2

We consider the filtering error system in (18) and Lyapunov functional (20). Similar to the proof of Theorem 1, by using the Lemma 1 and Lemma 2, (A2) can be rearranged as follows:

$$\begin{aligned} & {\{E}\left\{ \int _{U}\int _{0}^{t_{f}}e^{\mathrm{T}}\left( x,t\right) e\left( x,t\right) {\text {d}}t{\text {d}}x\right\} {\le E}\left\{ \int _{U}V\left( {\overline{y}}_{0}\left( x\right) \right) {\text {d}}x\right\} \\ &\quad {+\gamma }\left\{ E\int _{U}\int _{0}^{t_{f}}{\overline{v}} ^{\mathrm{T}}\left( x,t\right) {\overline{v}}\left( x,t\right) {\text {d}}t{\text {d}}x\right\} {+E}\int _{U}\int _{0}^{t_{f}}{\overline{y}}^{\mathrm{T}}\left( x,t\right) {Q}^{\mathrm{T}}{Q}{\overline{y}}\left( x,t\right) \\ &\quad {+\nabla }^{2}{\overline{y}}^{\mathrm{T}}\left( x,t\right) {\overline{D}}^{\mathrm{T}} {\overline{P}}{\overline{y}}\left( x,t\right) {+}{\overline{y}} ^{\mathrm{T}}\left( x,t\right) {\overline{P}}{\overline{D}}{\nabla }^{2} {\overline{y}}\left( x,t\right) {+}{\overline{y}}^{\mathrm{T}}\left( x,t\right) {\overline{A}}_{i}^{\mathrm{T}}{\overline{P}}{\overline{y}}\left( x,t\right) \\ &\quad {+}{\overline{y}}^{\mathrm{T}}\left( x,t\right) {\overline{P}}{\overline{A}}_{i} {\overline{y}}\left( x,t\right) {+}\frac{1}{\gamma }{\overline{y}} ^{\mathrm{T}}\left( x,t\right) {\overline{P}}{\overline{G}}_{v}{\overline{G}}_{v}^{\mathrm{T}} {\overline{P}}{\overline{y}}\left( x,t\right) \\ &\quad {+}{\overline{y}}^{\mathrm{T}}\left( x,t\right) {\overline{P}}{\overline{L}}_{i} {\overline{L}}_{i}^{\mathrm{T}}{\overline{P}}{\overline{y}}\left( x,t\right) {+} {\overline{\varepsilon }}^{\mathrm{T}}\left( y\left( x,t\right) \right) \overline{ \varepsilon }\left( y\left( x,t\right) \right) \\ &\quad {+}{\overline{y}}^{\mathrm{T}}\left( x,t\right) {\overline{A}}_{Wi}^{\mathrm{T}} {\overline{P}}{\overline{A}}_{Wi}{\overline{y}}\left( x,t\right) {+} {\overline{\varepsilon }}_{f_{W}}^{\mathrm{T}}\left( y\left( x,t\right) \right) {\overline{P}}{\overline{\varepsilon }}_{f_{W}}\left( y\left( x,t\right) \right) \\ &\quad {+}{\overline{y}}^{\mathrm{T}}\left( x,t\right) {\overline{A}}_{Wi}^{\mathrm{T}} {\overline{PP}}{\overline{A}}_{Wi}{\overline{y}}\left( x,t\right) {+} {\overline{\varepsilon }}_{f_{W}}^{\mathrm{T}}\left( y\left( x,t\right) \right) {\overline{\varepsilon }}_{f_{W}}\left( y\left( x,t\right) \right) \\ &\quad {+\lambda [}{\overline{y}}^{\mathrm{T}}\left( x,t\right) {\overline{N}} _{i}^{\mathrm{T}}{\overline{P}}{\overline{N}}_{i}{\overline{y}}\left( x,t\right) {+}{\overline{y}}^{\mathrm{T}}\left( x,t\right) {\overline{P}}{\overline{N}}_{i} {\overline{y}}\left( x,t\right) \\ &\quad {+}{\overline{y}}^{\mathrm{T}}\left( x,t\right) {\overline{N}}_{i}^{\mathrm{T}} {\overline{P}}{\overline{y}}\left( x,t\right) {+}{\overline{y}} ^{\mathrm{T}}\left( x,t\right) {P}{\overline{P}}{\overline{y}}\left( x,t\right) {+}{\overline{y}}^{\mathrm{T}}\left( x,t\right) {\overline{N}} _{i}^{\mathrm{T}}{\overline{P}}{\overline{P}}{\overline{N}}_{i}{\overline{y}}\left( x,t\right) \\ &\quad {+2}{\overline{\varepsilon }}_{\tau }^{\mathrm{T}}\left( y\left( x,t\right) \right) {\overline{\varepsilon }}_{\tau }\left( y\left( x,t\right) \right) {+}{\overline{\varepsilon }}_{\tau }^{\mathrm{T}}\left( y\left( x,t\right) \right) {{\bar{P}}}{\overline{\varepsilon }}_{\tau }\left( y\left( x,t\right) \right) {]{\text {d}}t{\text {d}}x\}} \end{aligned}$$

(B1)

Hence, if the following inequalities hold for $i=1,2,\ldots ,l$

$$\begin{aligned}&[{\overline{y}}^{\mathrm{T}}\left( x,t\right) {Q}^{\mathrm{T}}{Q} {\overline{y}}\left( x,t\right) {+\nabla }^{2}{\overline{y}} ^{\mathrm{T}}\left( x,t\right) {\overline{D}}^{\mathrm{T}}{\overline{P}}{\overline{y}}\left( x,t\right) {+}{\overline{y}}^{\mathrm{T}}\left( x,t\right) {\overline{P}} {\overline{D}}{\nabla }^{2}{\overline{y}}\left( x,t\right) \\&\qquad {+}{\overline{y}}^{\mathrm{T}}\left( x,t\right) {\overline{A}}_{i}^{\mathrm{T}} {\overline{P}}{\overline{y}}\left( x,t\right) {+}{\overline{y}} ^{\mathrm{T}}\left( x,t\right) {\overline{P}}{\overline{A}}_{i}{\overline{y}}\left( x,t\right) {+}\frac{1}{\gamma }{\overline{y}}^{\mathrm{T}}\left( x,t\right) {\overline{P}}{\overline{G}}_{v}{\overline{G}}_{v}^{\mathrm{T}}{\overline{P}}{\overline{y}} \left( x,t\right) \\&\qquad {+}{\overline{y}}^{\mathrm{T}}\left( x,t\right) {\overline{P}}{\overline{L}}_{i} {\overline{L}}_{i}^{\mathrm{T}}{\overline{P}}{\overline{y}}\left( x,t\right) {+} {\overline{\varepsilon }}^{\mathrm{T}}\left( y\left( x,t\right) \right) \overline{ \varepsilon }\left( y\left( x,t\right) \right) \\&\qquad {+}{\overline{y}}^{\mathrm{T}}\left( x,t\right) {\overline{A}}_{Wi}^{\mathrm{T}} {\overline{P}}{\overline{A}}_{Wi}{\overline{y}}\left( x,t\right) {+} {\overline{\varepsilon }}_{f_{W}}^{\mathrm{T}}\left( y\left( x,t\right) \right) {\overline{P}}{\overline{\varepsilon }}_{f_{W}}\left( y\left( x,t\right) \right) \\&\qquad {+}{\overline{y}}^{\mathrm{T}}\left( x,t\right) {\overline{A}}_{Wi}^{\mathrm{T}} {\overline{PP}}{\overline{A}}_{Wi}{\overline{y}}\left( x,t\right) {+} {\overline{\varepsilon }}_{f_{W}}^{\mathrm{T}}\left( y\left( x,t\right) \right) {\overline{\varepsilon }}_{f_{W}}\left( y\left( x,t\right) \right) \\&\qquad {+\lambda [}{\overline{y}}^{\mathrm{T}}\left( x,t\right) {\overline{N}} _{i}^{\mathrm{T}}{\overline{P}}{\overline{N}}_{i}{\overline{y}}\left( x,t\right) {+}{\overline{y}}^{\mathrm{T}}\left( x,t\right) {\overline{P}}{\overline{N}}_{i} {\overline{y}}\left( x,t\right) \\&\qquad {+}{\overline{y}}^{\mathrm{T}}\left( x,t\right) {\overline{N}}_{i}^{\mathrm{T}} {\overline{P}}{\overline{y}}\left( x,t\right) {+}{\overline{y}} ^{\mathrm{T}}\left( x,t\right) {P}{\overline{P}}{\overline{y}}\left( x,t\right) \\&\qquad {+}{\overline{y}}^{\mathrm{T}}\left( x,t\right) {\overline{N}}_{i}^{\mathrm{T}} {\overline{P}}{\overline{P}}{\overline{N}}_{i}{\overline{y}}\left( x,t\right) {+2}{\overline{\varepsilon }}_{\tau }^{\mathrm{T}}\left( y\left( x,t\right) \right) {\overline{\varepsilon }}_{\tau }\left( y\left( x,t\right) \right) \\&\qquad {+}{\overline{\varepsilon }}_{\tau }^{\mathrm{T}}\left( y\left( x,t\right) \right) {{\bar{P}}}{\overline{\varepsilon }}_{\tau }\left( y\left( x,t\right) \right) {]<0,} \end{aligned}$$

then the robust $H_{\infty }$ filtering performance in (10) on spatiotemporal domain U will be achieved if the effect of the initial state $V\left( {\overline{y}}_{0}\left( x\right) \right) \ne 0$, or the robust $H_{\infty }$ filter performance achieves to (9) if the effect of the initial state $V\left( {\overline{y}}_{0}\left( x\right) \right) =0$. $\square$

Appendix C: Proof of Theorem 3

Let us denote ${\overline{z}}=Q_{d}^{\frac{1}{2}}{\overline{y}}\left( x,t\right)$ and $Q_{d}={\overline{D}}^{\mathrm{T}}{\overline{P}}+{\overline{P}}{\overline{D}}$, then we get:

$$\begin{aligned} \left. \begin{array}{l} \nabla ^{2}{\overline{y}}^{\mathrm{T}}\left( x,t\right) {\overline{D}}^{\mathrm{T}}{\overline{P}} {\overline{y}}\left( x,t\right) +{\overline{y}}^{\mathrm{T}}\left( x,t\right) {\overline{P}} {\overline{D}}\nabla ^{2}{\overline{y}}\left( x,t\right) \\ \quad ={\overline{z}}\nabla ^{2}{\overline{z}}=\sum \limits _{i=1}^{n}{\overline{z}} _{i}\nabla ^{2}{\overline{z}}_{i} \end{array} \right. \end{aligned}$$

(C1)

where ${\overline{z}}=\left[ {\overline{z}}_{1}\ {\overline{z}}_{2}\ \cdots \ {\overline{z}}_{n}\right] ^{\mathrm{T}}$.

Based on the identity $\nabla \cdot \left( {\overline{z}}_{i}\nabla {\overline{z}}_{i}\right) ={\overline{z}}_{i}\nabla ^{2}{\overline{z}}_{i}+\left| \nabla {\overline{z}}_{i}^{2}\right|$, then we can rewrite (C1) as follows [43]:

$$\begin{aligned}&\nabla ^{2}{\overline{y}}^{\mathrm{T}}\left( x,t\right) {\overline{D}}^{\mathrm{T}}{\overline{P}} {\overline{y}}\left( x,t\right) +{\overline{y}}^{\mathrm{T}}\left( x,t\right) {\overline{P}} {\overline{D}}\nabla ^{2}{\overline{y}}\left( x,t\right) \nonumber \\&\quad =\sum \limits _{i=1}^{n}{\overline{z}}_{i}\nabla ^{2}{\overline{z}} _{i}=\sum \limits _{i=1}^{n}\nabla \cdot \left( {\overline{z}}_{i}\nabla {\overline{z}}_{i}\right) -\sum \limits _{i=1}^{n}\left| \nabla {\overline{z}} _{i}^{2}\right| \end{aligned}$$

(C2)

By using divergence theorem [43, 44] and the Neumann boundary condition and Dirichlet boundary condition in (2) with $\nabla {\overline{z}} _{i}\cdot \overrightarrow{n}_{a}=\frac{\partial {\overline{z}}_{i}}{\partial \overrightarrow{n}_{a}}$, then (C2) can be rewritten as [44, 45] :

$$\begin{aligned}&\int _{U}\sum \limits _{i=1}^{n}{\overline{z}}_{i}\nabla ^{2}{\overline{z}} _{i}{\text {d}}x=\oint \nolimits _{\partial U}\sum \limits _{i=1}^{n}\left( {\overline{z}} _{i}\nabla {\overline{z}}_{i}\right) \cdot \overrightarrow{n} _{a}{\text {d}}s-\int _{U}\sum \limits _{i=1}^{n}\left| \nabla {\overline{z}} _{i}\right| ^{2}{\text {d}}x \nonumber \\&\quad =\oint \nolimits _{\partial U}\sum \limits _{i=1}^{n}{\overline{z}}_{i}\left( \frac{\partial {\overline{z}}_{i}}{\partial \overrightarrow{n}_{a}}\right) {\text {d}}s-\int _{U}\sum \limits _{i=1}^{n}\left| \nabla {\overline{z}} _{i}\right| ^{2}{\text {d}}x=-\int _{U}\sum \limits _{i=1}^{n}\left| \nabla {\overline{z}}_{i}\right| ^{2}{\text {d}}x \end{aligned}$$

(C3)

Now, consider the eigenvalues of the Laplace operator $\nabla$ under Dirichlet boundary condition, which is defined as

$$\begin{aligned} \lambda _{k}^{(D)}=\sup \inf \frac{\int _{U}\left| \nabla \overline{z} \right| ^{2}{\text {d}}x}{\int _{U}\left| {\overline{z}}\right| ^{2}{\text {d}}x} \end{aligned}$$

(C4)

where the sup is taken over all choices of vector $\{\psi _{i}^{(D)}\}_{i=1}^{k-1}$ which are orthogonal basis to the set $D=\{y(x,t)\in L_{2}(U\times {\mathbb {R}} _{+}; {\mathbb {R}} ^{n})\mid y(x,t),\frac{\partial y(x,t)}{\partial x},\frac{\partial ^{2}y(x,t) }{\partial x^{2}}\in L_{2}(U\times {\mathbb {R}} _{+}; {\mathbb {R}} ^{n})\}$ and the inf is taken over all ${\overline{z}}\in D$ which is orthogonal to $\{\psi _{i}^{(D)}\}_{i=1}^{k-1}.$

The eigenvalues of laplace operator satisfy 0$<\lambda _{1}^{(D)}\le \lambda _{2}^{(D)}\le \lambda _{3}^{(D)}\le \lambda _{4}^{(D)}\le \cdots \le \lambda _{k}^{(D)}\le \cdots$. Also, the lowest eigenvalue $\lambda _{1}^{(D)}$ satisfies the following equality [28]:

$$\begin{aligned} \lambda _{1}^{(D)}=\inf _{{\overline{z}}\in D\backslash \{0\}}\frac{ \int _{U}\left| \nabla {\overline{z}}\right| ^{2}{\text {d}}x}{\int _{U}\left| {\overline{z}}\right| ^{2}{\text {d}}x} \end{aligned}$$

(C5)

Furthermore, we immediately have the following inequality:

$$\begin{aligned} -\int _{U}\left| \nabla {\overline{z}}\right| ^{2}{\text {d}}x\le -\lambda _{1}^{(D)}\int _{U}\left| {\overline{z}}\right| ^{2}{\text {d}}x,\forall {\overline{z}}\in D\backslash \{0\} \end{aligned}$$

(C6)

From (C2), (C3) , (C6) and integrating both sides from 0 to $t_{f}$ with respect to the variable t, we have the results.

$$\begin{aligned}&\int _{0}^{t_{f}}\int _{U}\nabla ^{2}{\overline{y}}^{\mathrm{T}}\left( x,t\right) {\overline{D}}^{\mathrm{T}}{\overline{P}}{\overline{y}}\left( x,t\right) +{\overline{y}} ^{\mathrm{T}}\left( x,t\right) {\overline{P}}{\overline{D}}\nabla ^{2}{\overline{y}}\left( x,t\right) {\text {d}}x{\text {d}}t \nonumber \\&\quad =-\int _{0}^{t_{f}}\int _{U}\left| \nabla {\overline{z}}\right| ^{2}{\text {d}}x{\text {d}}t\le -\lambda _{1}^{(D)}\int _{0}^{t_{f}}\int _{U}\left| \overline{z }\right| ^{2}{\text {d}}x{\text {d}}t \nonumber \\&\quad =-\lambda _{1}^{(D)}\int _{0}^{t_{f}}\int _{U}{\overline{y}}^{\mathrm{T}}\left( x,t\right) ({\overline{D}}^{\mathrm{T}}{\overline{P}}+{\overline{P}}{\overline{D}})\overline{y }\left( x,t\right) {\text {d}}x{\text {d}}t \end{aligned}$$

(C7)

Hence, we can choose $c_{p}=\lambda _{1}^{(D)}$ in Eq. (22) under Dirichlet boundary condition.

Now, we focus on the case Neumann boundary condition. Consider the eigenvalues of the Laplace operator $\nabla$ under Dirichlet boundary condition, which is defined as

$$\begin{aligned} \lambda _{k}^{(N)}=\sup \inf \frac{\int _{U}\left| \nabla \overline{z} \right| ^{2}{\text {d}}x}{\int _{U}\left| {\overline{z}}\right| ^{2}{\text {d}}x} \end{aligned}$$

(C8)

where the sup is taken over all choices of vector $\{\psi _{i}^{(N)}\}_{i=1}^{k-1}$ which are orthogonal basis of the set D and the inf is taken over all ${\overline{z}}\in D$ which is orthogonal to $\{\psi _{i}^{(D)}\}_{i=1}^{k-1}.$ Similar to the deviation of Eqs. (C1), (C2), (C3), (C4), (C6), (C7), we have the following results:

$$\begin{aligned}&\int _{0}^{t_{f}}\int _{U}\nabla ^{2}{\overline{y}}^{\mathrm{T}}\left( x,t\right) {\overline{D}}^{\mathrm{T}}{\overline{P}}{\overline{y}}\left( x,t\right) +{\overline{y}} ^{\mathrm{T}}\left( x,t\right) {\overline{P}}{\overline{D}}\nabla ^{2}{\overline{y}}\left( x,t\right) {\text {d}}x{\text {d}}t \nonumber \\&\quad \le -\lambda _{2}^{(N)}\int _{0}^{t_{f}}\int _{U}{\overline{y}}^{\mathrm{T}}\left( x,t\right) ({\overline{D}}^{\mathrm{T}}{\overline{P}}+{\overline{P}}{\overline{D}})\overline{y }\left( x,t\right) {\text {d}}x{\text {d}}t \end{aligned}$$

(C9)

Hence, we can choose $c_{p}=\lambda _{2}^{(D)}$ in Eq. (22) under Neumann boundary condition. Moreover, the eigenvalues $\lambda _{2}^{(N)},\lambda _{1}^{(D)}$ satisfy the following inequality [46,47,48] :

$$\begin{aligned} \frac{\pi ^{2}}{d(U)^{2}}\le \lambda _{2}^{(N)}\le \lambda _{1}^{(D)}, \end{aligned}$$

(C10)

where d(U) is the diameter of set U and U is any bounded convex domain.

Hence, Eqs. (C7) and (C9) can be written as

$$\begin{aligned}&\int _{0}^{t_{f}}\int _{U}\nabla ^{2}{\overline{y}}^{\mathrm{T}}\left( x,t\right) {\overline{D}}^{\mathrm{T}}{\overline{P}}{\overline{y}}\left( x,t\right) +{\overline{y}} ^{\mathrm{T}}\left( x,t\right) {\overline{P}}{\overline{D}}\nabla ^{2}{\overline{y}}\left( x,t\right) {\text {d}}x{\text {d}}t \nonumber \\&\quad \le -\frac{\pi ^{2}}{d(U)^{2}}\int _{0}^{t_{f}}\int _{U}{\overline{y}} ^{\mathrm{T}}\left( x,t\right) ({\overline{D}}^{\mathrm{T}}{\overline{P}}+{\overline{P}}{\overline{D}} ){\overline{y}}\left( x,t\right) {\text {d}}x{\text {d}}t \end{aligned}$$

(C11)

In other words, the constant $c_{p}$ can be chosen as $\frac{\pi ^{2}}{ d(U)^{2}}$ under the Dirichlet boundary condition and Neumann boundary condition if the domain U is bounded and convex. We finish the proof of Theorem 3. $\square$

Appendix D: Proof of Theorem 4

By using the result in Theorem 3 with bounds of the fuzzy approximation errors in (19) and constraints (24), (B1) can be rearranged as follows:

$$\begin{aligned}&\left. E\left\{ \int _{U}\int _{0}^{t_{f}}e^{\mathrm{T}}\left( x,t\right) e\left( x,t\right) {\text {d}}t{\text {d}}x\right\} \le E\left\{ \int _{U}V\left( {\overline{y}}_{0}\left( x\right) \right) {\text {d}}x\right\} \right. \nonumber \\&\qquad +E\int _{U}\int _{0}^{t_{f}}{\overline{y}}^{\mathrm{T}}\left( x,t\right) [Q^{\mathrm{T}}Q-c_{p}Q_{d}+{\overline{A}}_{i}^{\mathrm{T}}{\overline{P}}+{\overline{P}}{\overline{A}} _{i} \nonumber \\&\qquad +\frac{1}{\gamma }{\overline{P}}{\overline{G}}_{v}{\overline{G}}_{v}^{\mathrm{T}}\overline{P }+{\overline{P}}{\overline{L}}_{i}{\overline{L}}_{i}^{\mathrm{T}}{\overline{P}}+\xi + {\overline{A}}_{Wi}^{\mathrm{T}}{\overline{P}}{\overline{A}}_{Wi}+{\overline{A}}_{Wi}^{\mathrm{T}} {\overline{P}}{\overline{P}}{\overline{A}}_{Wi} \nonumber \\&\qquad +\lambda ({\overline{N}}_{i}^{\mathrm{T}}{\overline{P}}{\overline{N}}_{i}+{\overline{N}} _{i}^{\mathrm{T}}{\overline{P}}{\overline{P}}{\overline{N}}_{i}+{\overline{P}}{\overline{N}} _{i}+{\overline{N}}_{i}^{\mathrm{T}}{\overline{P}}+{\overline{P}}{\overline{P}})]{\overline{y}} \left( x,t\right) {\text {d}}t{\text {d}}x \nonumber \\&\qquad +\gamma E\left\{ \int _{U}\int _{0}^{t_{f}}{\overline{v}}^{\mathrm{T}}\left( x,t\right) {\overline{v}}\left( x,t\right) {\text {d}}t{\text {d}}x\right\} \end{aligned}$$

(D1)

with $\xi = {\text {diag}}((\sigma _{1}+(2+a+b)\sigma _{2}+(4+a+b)\lambda \sigma _{3}+\sigma _{4})I$ , 0).

If the following Riccati-like inequalities hold

$$\begin{aligned}&Q^{\mathrm{T}}Q-c_{p}Q_{d}+{\overline{A}}_{i}^{\mathrm{T}}{\overline{P}}+{\overline{P}}{\overline{A}} _{i}+\frac{1}{\gamma }{\overline{P}}{\overline{G}}_{v}{\overline{G}}_{v}^{\mathrm{T}} {\overline{P}} \nonumber \\&\qquad +{\overline{P}}{\overline{L}}_{i}{\overline{L}}_{i}^{\mathrm{T}}{\overline{P}}+\xi +\overline{ A}_{Wi}^{\mathrm{T}}{\overline{P}}{\overline{A}}_{Wi}+{\overline{A}}_{Wi}^{\mathrm{T}}{\overline{P}} {\overline{P}}{\overline{A}}_{Wi} \nonumber \\&\qquad +\lambda ({\overline{N}}_{i}^{\mathrm{T}}{\overline{P}}{\overline{N}}_{i}+{\overline{N}} _{i}^{\mathrm{T}}{\overline{P}}{\overline{P}}{\overline{N}}_{i}+{\overline{P}}{\overline{N}} _{i}+{\overline{N}}_{i}^{\mathrm{T}}{\overline{P}}+{\overline{P}}{\overline{P}})<0 \end{aligned}$$

(D2)

then the $H_{\infty }$ filtering performance in (9) or (10) is achieved.

Next, by applying the Schur complement and substituting matrices in (18) to (D2) , the Riccati-like inequalities in (D2) can be rearranged the following LMI with $Y_{i}=P_{2}L_{i}$:

$$\begin{aligned} {\tiny \begin{array}{c} \left[ \begin{array}{ccccccccc} \theta _{1}^{i} & 0 & N_{i}^{\mathrm{T}}P_{1} &{} 0 &{} P_{1} &{} 0 &{} N_{i}^{\mathrm{T}}P_{1} &{} 0 &{} P_{1}g_{v} \\ *&{} \theta _{2}^{i} &{} 0 &{} N_{i}^{\mathrm{T}}P_{2} &{} 0 &{} P_{2} &{} 0 &{} N_{i}^{\mathrm{T}}P_{2} &{} P_{2}g_{v} \\ *&{} *&{} -\frac{1}{\lambda }P_{1} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ *&{} *&{} *&{} -\frac{1}{\lambda }P_{2} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ *&{} *&{} *&{} *&{} -\frac{1}{\lambda }I &{} 0 &{} 0 &{} 0 &{} 0 \\ *&{} *&{} *&{} *&{} *&{} -\frac{1}{\lambda }I &{} 0 &{} 0 &{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} -\frac{1}{\lambda }I &{} 0 &{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} -\frac{1}{\lambda }I &{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} -\gamma I \\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *\\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *\\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *\\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *\\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *\\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *\\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} *\end{array} \right. \\ \left. \begin{array}{ccccccc} 0 &{} A_{wi}^{\mathrm{T}}P_{1} &{} 0 &{} A_{wi}^{\mathrm{T}}P_{1} &{} 0 &{} P_{1} &{} 0 \\ Y_{i}E_{m} &{} 0 &{} A_{wi}^{\mathrm{T}}P_{2} &{} 0 &{} A_{wi}^{\mathrm{T}}P_{2} &{} P_{2} &{} -Y_{i} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ -\gamma I &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ *&{} -P_{1} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ *&{} *&{} -P_{2} &{} 0 &{} 0 &{} 0 &{} 0 \\ *&{} *&{} *&{} -I &{} 0 &{} 0 &{} 0 \\ *&{} *&{} *&{} *&{} -I &{} 0 &{} 0 \\ *&{} *&{} *&{} *&{} *&{} -I &{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} -I \end{array} \right] \end{array} }<0 \end{aligned}$$

(D3)

where $\theta _{1}^{i}=A_{i}^{\mathrm{T}}P_{1}+P_{1}A_{i}+\lambda \left( N_{i}^{\mathrm{T}}P_{1}+P_{1}N_{i}\right) -c_{p}(DP_{1}+P_{1}D^{\mathrm{T}})+(\sigma _{1}+(2+a+b)\sigma _{2}+(4+a+b)\lambda \sigma _{3}+\sigma _{4})I_{3\times 3}$, $\theta _{2}^{i}=\lambda N_{i}^{\mathrm{T}}P_{2}+\lambda P_{2}N_{i}+A_{i}^{\mathrm{T}}P_{2}+P_{2}A_{i}-Y_{i}C_{i}-C_{i}^{\mathrm{T}}Y_{i}^{\mathrm{T}}-c_{p}(D^{\mathrm{T}}P_{2}+P_{2}D)+I$.i.e., if the LMIs in (D6) and (25) are with the solution $a>0$,$b>0$, $P_{1}>0$, $P_{2}>0$ and $Y_{i}$, then the robust $H_{\infty }$ filter performance in (10) on spatiotemporal domain U is achieved if the effect of the initial state $V\left( {\overline{y}}_{0}\left( x\right) \right) \ne 0$, or the robust $H_{\infty }$ filter performance in (9) is achieved if the effect of the initial state $V\left( {\overline{y}}_{0}\left( x\right) \right) =0$. We finish the proof of Theorem 4. $\square$