Introduction

Leptospirosis is a worldwide zoonotic disease which is commonly occurs in tropical and subtropical regions. The magnitude of the problem in the tropics and subtropics may be largely not only because of their climatic and environmental conditions, but also likely relationship with the caused leptospira contaminated environment, such as local agricultural practices and poor housing and disposal, all what will be many sources of infection [1, 2]. In tropical countries, people are always risky, especially if their contact with potentially infected areas, rodents and pets in a wet and hot climate. In template climate, the cattle, pits and dogs are the carriers for important source of leptospirosis [3]. Valuable information about the risk factor of leptospirosis disease can be found in [4].

To better understand the epidemiology of an infectious disease, mathematical modeling has played an important role [5–8]. These models provide us the quantitative descriptions of the complicated, non linear process of disease transmission and help us to obtain inside into the dynamics of the disease and we are able to make such decision for public health policy. Many mathematical models [9–11] have been proposed to represent the compartmental dynamics of both susceptible, infected and recovered human and vector population.

Various mathematical studies have been proposed on leptospirosis disease. Here, we give an overview. Triampo et al. presented a mathematical model for the transmission of leptospirosis disease in [12]. In their work, they considered a number of leptospirosis disease in Thailand and shown their numerical simulations. Zaman [13] considered the real data presented in [12] to studied the dynamical behavior and role of optimal control theory of this disease. Pongsumpun et al. [14] developed mathematical model to study the behavior of leptospirosis disease. In their work, they represent the rate of change for both the vector (rats) and human population. They divided the human population further into two main groups Juveniles and adults. Moreover, we refer the reader to see [15–17] and the references therein.

In epidemic models a variety of non linear incidence rate have been used [18–20]. Liu et al. [21] showed that the case where hosts can exhibit prolonged immunity to infection is not linear incidence rate of infection could greatly expand the breadth dynamics caused by this disease. The saturated incidence was first time used by Capasso and Serio [20] in cholera epidemic model.

In this work, we present analysis of nonlinear incidence in leptospirosis epidemic model. Here, we study the model presented in [22]. In [22], the authors used the standard optimal control technique Pontryagin’s Maximum Principle and used three control variables for possible eradication of the infection in the community. We study the model [22], to obtain its stability analysis on behalf of reproduction number. First, we find the threshold/ basic reproduction number for the model and then show that the Disease free equilibrium is locally as well as globally asymptotically stable for \(R_0< 1\) and unstable for \(R_0>1\). Further, we find that an endemic equilibrium is locally as well as globally asymptotically stable for \(R_0>1\). The global stability of an endemic equilibrium is shown by the geometric approach method. We solve, the proposed model numerically and the results are presented in the form of plots for justification purpose. Finally, the conclusion and references are presented.

This paper is organized as follows: section “Mathematical Model” is devoted to the mathematical formulation of the model. We discuss the equilibria and local stability of both the disease-free and endemic equilibrium in section “Equilibria and Local Stability”. In section “Global Stability”, we show the global stability of both the disease-free and endemic equilibrium. In section “Numerical Simulations” the theoretical results are demonstrated in the form of numerical graphics. Finally, we conclude our work by conclusion in section “Conclusion”.

Mathematical Model

In this section, we present the model formulation of the leptospirosis disease with their interaction with human population. The human population denoted by \(N_h(t)\), is subdivided into three compartments; \(S_h(t)\)-Susceptible individuals, \(I_h(t)\)-infected individuals (those who have been infected) and \(R_h(t)\)-recovered individuals(those who recovered from infection or removed), so

$$\begin{aligned} N_h(t)=S_h(t)+I_h(t)+R_h(t). \end{aligned}$$
(1)

The population of susceptible is increased by recruitment of the individuals (which is assumed susceptible), at the rate of \(b_h\). The susceptible population decreased by following the effective contact with the infected individuals and vectors (in the \(I_h\) and \(I_v\)) at a rate \(\lambda (t)\), where

$$\begin{aligned} \lambda (t)=\left( \frac{\beta _2 I_v}{1+\alpha _1 I_v}+\frac{\beta _1 I_h}{1+\alpha _2 I_h}\right) . \end{aligned}$$
(2)

In (2), \(\beta _2\) and \(\beta _1\) are the effective contact rate (capable of leading to infection). The population of susceptible is further decreased with the natural death \(\mu _h\), while increased with the number of individuals, which are susceptible again at a rate of \(\lambda _h\). So, we can write, the rate of change of the susceptible population given by

$$\begin{aligned} \frac{dS_h}{dt}= & {} b_h-\mu _h S_h -S_h \lambda (t)+\lambda _h R_h. \end{aligned}$$
(3)

The population of infected individuals is generated by the infection of susceptible individuals (at a rate \(\lambda (t)\)). The population of infected individuals is decreased by the natural mortality rate \(\mu _h\), disease induced death rate \(\delta _h\) and from the recovery rate of infection \(\gamma _h\). So, we can write their rate of change for infected population given by

$$\begin{aligned} \frac{dI_h}{dt}= & {} S_h\lambda (t)-(\mu _h+\delta _h+\gamma _h)I_h. \end{aligned}$$
(4)

The population of recovered individuals is generated by the rate of recovery \(\gamma _h\) (from infected class), while decreased by the natural death rate \(\mu _h\) and \(\lambda _h\) (those individuals who susceptible again). Thus, their rate of change can be expressed as follows:

$$\begin{aligned} \frac{dR_h}{dt}= & {} \gamma _h I_h-(\mu _h+\lambda _h)R_h. \end{aligned}$$
(5)

The vector population is denoted by \(N_v(t)\), is subdivided into two classes, \(S_v(t)\)-susceptible vector and \(I_v(t)\)-infected vector, so

$$\begin{aligned} N_v(t)=S_v(t)+I_v(t). \end{aligned}$$
(6)

The population of susceptible vector is generated by the recruitment of the vector at a rate of \(b_v\). The population of susceptible is decreased by following the effective contact with infected individuals \(I_h\) (at a rate of \(\overline{\lambda (t)})\), where \(\overline{\lambda (t)}=\beta _3 I_h/1+\alpha _2 I_h\) and \(\beta _3\) is the effective contact rate that leads to infection. Also, the population of susceptible vector is decreased by the natural death rate at a rate \(\gamma _v\). Thus, the rate of change for the susceptible vector is given by

$$\begin{aligned} \frac{dS_v}{dt}= & {} b_v-\gamma _v S_v- \overline{\lambda (t)}S_v. \end{aligned}$$
(7)

The population of infected vector is generated by the infection of susceptible vector at rate of \(\overline{\lambda (t)}\), while decreased by the natural death \(\gamma _v\) and disease related death rate \(\delta _v\). Their rate of change can be written as:

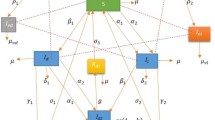
$$\begin{aligned} \frac{dI_v}{dt}= & {} \overline{\lambda (t)}S_v-\gamma _v I_v-\delta _v I_v. \end{aligned}$$
(8)

The complete transfer flow diagram of human and vector population is depicted in Fig. 1. Thus, the system for the transmission dynamics of the leptospirosis disease is given by the following nonlinear system of differential equations:

$$\begin{aligned} \begin{aligned} \frac{dS_h}{dt}&=b_h-\mu _h S_h -S_h \lambda (t)+\lambda _h R_h,\quad S_h(0)=S_0\ge 0,\\ \frac{dI_h}{dt}&=S_h\lambda (t)-(\mu _h+\delta _h+\gamma _h)I_h,\quad I_h(0) =I_0\ge 0,\\ \frac{dR_h}{dt}&=\gamma _h I_h-(\mu _h+\lambda _h)R_h,\quad R_h(0)=R_0\ge 0,\\ \frac{dS_v}{dt}&=b_v-\gamma _v S_v- \overline{\lambda (t)}S_v,\quad S_v(0)=S_0\ge 0,\\ \frac{dI_v}{dt}&=\overline{\lambda (t)}S_v-\gamma _v I_v-\delta _v I_v,\quad I_v(0)=I_0\ge 0, \end{aligned} \end{aligned}$$
(9)

Subject to nonnegative initial conditions.

Fig. 1
figure 1

The flow diagram of human and vector interaction

Full size image

One infected human will shed leptospirosis in their urine during and after the illness of the period, and thus may pose a risk of infection to others but only in a certain ways. Chief social interaction is perfectly safe, as airborne bacteria. Saliva is not consider high risky, because the bacteria cannot be tolerate the acidity of the human mouth for a long time, so even we advise against the risk of sharing food, cups or cutlery very small. Items that can dry out between uses, such as towels, also very low risk once they dry, but handle very blood soaked clothing, wet bed or similar may present risks, for detail see the reference [23]. Let \(N(h)=S_h+I_h+R_h\), shows the total dynamics of human population at time t, is given by

$$\begin{aligned} \frac{dN_{h}}{dt}=b_h-\mu _{h}N_{h}-\delta _{h}I_{h}\le b_h-\mu _{h}N_{h}, \end{aligned}$$

\(N(v)=S_v+I_v\), represent the total population of vector at time t, given by

$$\begin{aligned} \frac{dN_v}{dt}=b_v-N_{v}\gamma _{v}-\delta _{v} I_{v}\le b_v-N_{v}. \end{aligned}$$

The feasible region for the system (9) is

$$\begin{aligned} \Pi =\left( (S_h,I_h,R_h,S_v,I_v)\in {\mathbb {R}}_{+}^{5}, \quad \left( N_h\le \frac{b_h}{\mu _h}, N_v\le \frac{b_v}{\gamma _v}\right) \right) . \end{aligned}$$

It is easy to prove that the set \(\Pi \) is positively invariant with respect to system (9).

Lemma 2.1

Let the initial data \(S_h(0)>0, I_h(0)>0, R_h(0)>0, S_v(0)>0\) and \(I_v(0)>0\). Then the solution of \(S_h(t), I_h(t), R_h(t), S_v(t)\) and \(I_v(t)\) corresponding to model (9), are non-negative \(\forall \) time \(t>0\).

Proposition 2.1

Let \((S_h,I_h,R_h,S_v,I_v)\), be the solution of the system (9) with non-negative initial conditions and closed set

\(\Pi =((S_h, I_h, R_h, S_v, I_v)\in R_{+}^{5}, N_h\le \frac{b_h}{\mu _h},N_v\le \frac{b_v}{\gamma _v}),\) then \(\Pi \) is positively invariant and attracting under the flow described by system (9).

Proof

Consider the Lyapunov function

$$\begin{aligned} M(t)=(N_{h}(t), N_{v}(t)) =(S_h+I_h+R_h, S_v+I_v). \end{aligned}$$
(10)

The time derivative of Eq. (10) is

$$\begin{aligned} \frac{dM}{dt}=(b_h-\mu _h N_h- \delta _h I_h, \quad b_v-\gamma _v N_v-\delta _v I_v). \end{aligned}$$
(11)

Now it is easy to prove that

$$\begin{aligned} \frac{dN_h}{dt}\le & {} b_h-\mu _h N_h\le 0 \qquad for\quad \quad N_h\ge \frac{b_h}{\mu _h},\nonumber \\ \frac{dN_v}{dt}\le & {} b_v-\gamma _v N_v\le 0 \qquad for\quad \quad N_v\ge \frac{b_v}{\gamma _v}. \end{aligned}$$
(12)

Thus, it follows that \(\frac{dM}{dt}\le 0\) which implies that \(\Pi \) is positively invariant set. Also a standard comparison theorem [24] is used to show that

$$\begin{aligned} 0 \le (N_{h}, N_{v})\le ((N_h(0) e^{-\mu _{h} t} +\frac{b_{h}}{\mu _{h}}(1-e^{-\mu _{h} t}), \quad N_v(0) e^{-\gamma _{v} t}+\frac{b_v}{\gamma _{v}} (1-e^{-\gamma _{v} t})). \end{aligned}$$

Thus as t \(\rightarrow \) \(\infty \), 0 \(\le \) \((N_h,N_v)\) \(\le \) \((\frac{b_h}{\mu _h}\), \(\frac{b_v}{\gamma _v})\) and so \(\Pi \) is an attracting and positive invariant set. \(\square \)

Equilibria and Local Stability

To obtain the endemic equilibria of the system (9), setting the left side of the system (9) equal to zero, we get

$$\begin{aligned} \left\{ \begin{array}{ll} S^*_{h}=\frac{P_2 (1+\alpha _2 I^{*}_h)\left( P_1(\gamma _v(1+\alpha _2 I^*_h)+\beta _3 I^*_h)+\alpha _1 \beta _3 b_vI^{*}_h\right) }{\beta _2 \beta _3 b_v(1+\alpha _2 I^*_h)+\beta _1 \left( P_1 (\gamma _v (1+\alpha _2 I^*_h)+\beta _3 I^*_h)+\alpha _1 \beta _3b_v I^*_h\right) },\\ R^*_{h}=\frac{\gamma _h I^*_h}{(\mu _h+\delta _h)}, \\ S^*_{v}=\frac{b_v(1+\alpha _2 I^*_h)}{(\gamma _v(1+\alpha _2 I^*_h)+\beta _3 I^*_h)} \\ I^*_v=\frac{\beta _3b_vI^*_h}{(\gamma _v+\delta _v)(\gamma _v(1+\alpha _2 I^*_h)+\beta _3 I^*_h)}, \end{array} \right. \end{aligned}$$

where \(P_1=(\gamma _v+\delta _v),\qquad P_2=(\mu _h+\delta _h+\gamma _h)\),      \( P_3=(\mu _h+\lambda _h)\).

The disease free equilibrium of the system (9) at \(E_0\) is

$$\begin{aligned} S^0_h=\frac{b_h}{\mu _h},\quad S^0_v=\frac{b_v}{\gamma _v}. \end{aligned}$$

The basic reproduction number \(R_0\) for system (9) is

$$\begin{aligned} R_0=\frac{b_h\beta _2\beta _3 b_v+\beta _1(\gamma _v+\delta _v)b_h\gamma _v}{\mu _h(\gamma _v+\delta _v) (\mu _h+\delta _h+\gamma _h)\gamma _v}. \end{aligned}$$

Disease Free Local Stability

Theorem 3.1

For \(R_0< 1\), the DFE of the model (9) at \(E_0\) is stable locally asymptotically if \(((\mu _h+\delta _h+\gamma _h)-\beta _1b_h/\mu _h)>0\), otherwise unstable.

Proof

To show the local stability of the disease free equilibrium, we setting the left side of the system (9), equating to zero, we get the following jacobian matrix \(J_o\)

$$\begin{aligned} J_{o}=\left( \begin{array}{ccccc} -\mu _h &{} -\beta _1 S^o_h &{} \lambda _h &{} 0 &{} -\beta _2 S^o_h\\ \\ 0 &{} \beta _1 S^o_h-(\mu _h+\delta _h+\gamma _h) &{} 0 &{} 0 &{} \beta _2 S^o_h\\ \\ 0 &{} \gamma _h &{} -(\mu _h+\lambda _h) &{}0 &{} 0\\ \\ 0 &{} -\beta _3S^o_v &{} 0 &{} -\gamma _v &{} 0\\ \\ 0 &{} \beta _3S^o_v &{} 0 &{} 0 &{} -(\gamma _v+\delta _v) \end{array}\right) . \end{aligned}$$

The characteristics equation to the Jacobian matrix \(J_{o}\) is follows as

$$\begin{aligned} (\mu _h+\lambda )(\gamma _v+\lambda )(\lambda ^3+a_1\lambda ^2+a_2\lambda +a_3)=0, \end{aligned}$$
(13)

where,

$$\begin{aligned} a_1= & {} (\mu _h+\lambda _h)+(\gamma _v+\delta _v)+(\mu _h+\delta _h+\gamma _h)-\frac{\beta _1b_h}{\mu _h},\\\\a_2= & {} (\mu _h+\lambda _h)\Big ((\mu _h+\delta _h+\gamma _h)-\frac{\beta _1b_h}{\mu _h}\Big )+(\mu _h+\lambda _h)(\gamma _v+\delta _v)\\\\&+(\mu _h+\delta _h+\gamma _h)(\gamma _v+\delta _v)(1-R_0),\\\\a_3= & {} (\mu _h+\lambda _h)(\mu _h+\delta _h+\gamma _h)(\gamma _v+\delta _v)(1-R_0). \end{aligned}$$
(14)

Clearly, the two roots of the characteristics equation (14) are \(-\mu _h\) and \(-\gamma _v\) have negative real parts. The other roots can be determined from the cubic terms of the characteristics equation (14). Direct calculations by using (15), we get

$$\begin{aligned} a_1a_2-a_3= & {} \Big [(\mu _h+\lambda _h)+(\gamma _v+\delta _v)+(\mu _h+\delta _h+\gamma _h)-\frac{\beta _1b_h}{\mu _h}\Big ]\\\\&\times \Big [(\mu _h+\lambda _h)\Big \{(\gamma _v+\delta _v)+\Big ((\mu _h+\delta _h+\gamma _h)-\frac{\beta _1b_h}{\mu _h}\Big )\Big \}\Big ] \\\\&+(\gamma _v+\delta _v)\Big ((\mu _h+\delta _h+\gamma _h)-\frac{\beta _1b_h}{\mu _h}\Big )(\gamma _v+\delta _v)(\mu _h+\delta _h+\gamma _h)(1-R_0)>0. \end{aligned}$$

It follows from Routh-Hurwitz crietria, \(a_i>0\) for \(i=1, 2, 3\) and \(a_1a_2-a_3>0\). Thus, all the eigenvalues of the system (9) have negative real parts if \(R_0<1\) and \(((\mu _h+\delta _h+\gamma _h)-\beta _1b_h/\mu _h)>0\). Therefore, the system (9) at the disease free equilibrium \(E_0\) is locally asymptotically stable, if \(R_0<1\) and \(((\mu _h+\delta _h+\gamma _h)-\beta _1b_h/\mu _h)>0\). \(\square \)

The stability of the Disease free equilibrium of the system (9) for \(R_0< 1\) means that the disease dies out from the community. In this case the endemic equilibrium does not exists but we are interesting to find the properties of the model about the endemic equilibrium point \(E_1\), when \(R_0>1\). In the following, we show that the endemic equilibrium point \(E_1\) of the model (9) is locally asymptotically stable, when \(R_0>1\).

Local Stability of Endemic Equilibrium

In this subsection, we discuss the local stability of the model (9) at \(E_1\), by setting the left hand side of the system (9), equal to zero, we get the Jacobian matrix \(J^{*}\) in the following theorem.

Theorem 3.2

For \(R_0>1\), the endemic equilibrium point \(E_1\) of the system (9) is locally asymptotically stable if condition (18) and the terms under braces are positive, otherwise unstable.

Proof

The Jacobian matrix \(J^{*}\) of the system (9) at \(E_1\) is given by

$$\begin{aligned} J^{*}=\left[ \begin{array}{ccccc} -\mu _h-\frac{\beta _2 I^*_v}{1+\alpha _1 I^*_v}-\frac{\beta _1 I^*_h}{1+\alpha _2 I^*_h}&{}-\frac{\beta _1 S^*_h}{(1+\alpha _2 I^*_h)^2} &{} \lambda _h &{} 0 &{} -\frac{\beta _2 S^*_h}{(1+\alpha _1 I^*_v)^2} \\ \\ \frac{\beta _2 I^*_v}{1+\alpha _1 I^*_v}+\frac{\beta _1 I^*_h}{1+\alpha _2 I^*_h} &{} \frac{\beta _1 S^*_h}{(1+\alpha _2 I^*_h)^2}-(\mu _h+\delta _h+\gamma _h) &{} 0 &{} 0 &{} \frac{\beta _2 S^*_h}{(1+\alpha _1 I^*_v)^2}\\ \\ 0 &{} \gamma _h &{} -(\mu _h+\lambda _h) &{} 0 &{} 0\\ \\ 0 &{} -\frac{\beta _3 S^*_v}{(1+\alpha _2 I^*_h)^2} &{} 0 &{} -\gamma _v-\frac{\beta _3 I^*_h}{1+\alpha _2 I^*_h} &{} 0\\ \\ 0 &{} \frac{\beta _3 S^*_v}{(1+\alpha _2 I^*_h)^2} &{} 0 &{} \frac{\beta _3 I^*_h}{1+\alpha _2 I^*_h} &{} -(\gamma _v+\delta _v) \end{array}\right] . \end{aligned}$$
(15)

The characteristics equation of (15) is given by

$$\begin{aligned} \lambda ^5+A_1\lambda ^4+A_2\lambda ^3+A_3\lambda ^2+A_4\lambda +A_5=0, \end{aligned}$$
(16)

where

$$\begin{aligned} A_1= & {} B_4+\underbrace{(\mu _h+\lambda _h)-(B_1+B_3)}+(\gamma _v+\delta _v),\\\\A_2= & {} B_4(\gamma _v+\delta _v)+B_5B_6+(\underbrace{(\mu _h+\lambda _h)-(B_1+B_3)})(B_4+(\gamma _v+\delta _v))\\\\&+ \underbrace{[(B_2B_7-B_1B_3)-(B_3+B_1)(\mu _h+\lambda _h)]},\\\\A_3= & {} \underbrace{(\mu _h+\lambda _h)[B_2B_7-B_1B_3]-B_2\gamma _h\lambda _h}+\underbrace{[(B_2B_7-B_1B_3)-(B_3+B_1)(\mu _h+\lambda _h)]}\\\\&\times [B_4+(\gamma _v+\delta _v)]+[\underbrace{(\mu _h+\lambda _h)-(B_1+B_3)}]B_4(\gamma _v+\delta _v) +[(2\mu _h+\lambda _h)+\gamma _v]B_5B_6,\\\\ A_4= & {} \underbrace{\{(\mu _h+\lambda _h)[B_2B_7-B_1B_3]-B_2\gamma _h\lambda _h\}}[B_4+(\gamma _v+\delta _v)]\\\\&+B_4(\gamma _v+\delta _v)\underbrace{[(B_2B_7-B_1B_3)-(B_3+B_1)(\mu _h+\lambda _h)]} \\\\&+[(2\mu _h+\lambda _h)\gamma _v+\mu _h(\mu _h+\lambda _h)]B_5B_6,\\\\A_5= & {} B_4(\gamma _v+\delta _v)\underbrace{\{(\mu _h+\lambda _h)[B_2B_7-B_1B_3]-B_2\gamma _h\lambda _h\}}+B_5B_6\mu _h(\mu _h+\lambda _h)\gamma _v, \end{aligned}$$
(17)

and

$$\begin{aligned} B_1= & {} \mu _h+\frac{\beta _1I_h}{1+\alpha _2I_h}+\frac{\beta _2I_v}{1+\alpha _1I_v}, ~B_2=\frac{\beta _1I_h}{1+\alpha _2I_h}+\frac{\beta _2I_v}{1+\alpha _1I_v},~\\ B_3= & {} \frac{\beta _1S^*_h}{(1+\alpha _2I_h)^2}-(\mu _h+\delta _h+\gamma _h),\\\\B_4= & {} (\gamma _v+\frac{\beta _3I_h}{1+\alpha _2I_h}), B_5=\frac{\beta _3S_v}{(1+\alpha _2I_h)^2}, B_6=\frac{\beta _2S_h}{(1+\alpha _1I_v)^2},\\\\B_7= & {} \frac{\beta _1S_h}{(1+\alpha _2I_h)^2}, ~B_8=\frac{\beta _3I_h}{(1+\alpha _2I_h)} \end{aligned}$$

The Routh-Hurwitz criteria for (16) is follows as

$$\begin{aligned} H_5= & {} \left| \begin{array}{ccccc} A_1 &{} A_3 &{} A_5 &{} 0 &{} 0 \\ 1 &{} A_2 &{} A_4 &{} 0 &{} 0 \\ 0 &{} A_1 &{} A_3 &{} A_5 &{} 0 \\ 0 &{} 1 &{} A_2 &{} A_4 &{} 0 \\ 0 &{} 0 &{} A_1 &{} A_3 &{} A_5 \\ \end{array} \right| =A_1A_4A_5(A_2A_3-A_1A_4)-A_1A^2_2A^2_5\\\\&+A_1A_4A^2_5-A_4A_5(A^2_3-A_1A_5)+A_2A_3A^2_5-A^2_5>0 \end{aligned}$$
(18)

The eigenvalues of the characteristics equations (16) have negative real parts if \(A_i>0\) for \(i=1, 2, 3, 4, 5\), \(H_5>0\) and \(R_0>1\) and the terms under braces in positive. Thus, it follows from Routh-Hurtwiz criteria that the system (9) at the endemic equilibrium point \(E_1\) is locally asymptotically stable, if \(R_0>1\) and the terms under braces are positive and the conditions (18) are satisfied.\(\square \)

Global Stability

In this section, we investigate the global stability of the system (9) at the disease free equilibrium \(E_0\) and the endemic equilibrium at \(E_2\). In the following theorem, we first show the disease free global stability for the case \((\lambda _h = 0)\).

Theorem 4.1

The system (9) at \(E_0\) is globally asymptotically stable if \(R_0 < 1\), otherwise unstable.

Proof

In order to show this result, we construct the following lyapanove function:

$$\begin{aligned} L(t)= & {} (\gamma _v+\delta _v)\Big (S_h-S^0_h-S^0_h \log \frac{ S_h}{S^0_h}\Big )+(\gamma _v+\delta _v)I_h+\frac{\beta _2b_h}{\mu _h}\Big (S_v-S^0_v-S^0_v\log \frac{ S_v}{S^0_v}\Big )\\\\&+\frac{\beta _2b_h}{\mu _h} I_v. \end{aligned}$$
(19)

Taking the time derivative of (19) along the solutions of system (9), we obtain

$$\begin{aligned} L'(t)= & {} (\gamma _v+\delta _v)\Big (\frac{S_h-S^0_h}{S_h}\Big )[b_h-\mu _h S_h -(\frac{\beta _1I_h}{1+\alpha _2 I_h}+\frac{\beta _2I_v}{1+\alpha _1 I_v})S_h]\\\\&+(\gamma _v+\delta _v)[(\frac{\beta _1I_h}{1+\alpha _2 I_h}+\frac{\beta _2I_v}{1+\alpha _1 I_v})S_h-(\mu _h+\delta _h+\gamma _h)I_h]\\\\&+\frac{\beta _2b_h}{\mu _h}\Big (\frac{S_v-S^0_v}{S_v}\Big )[b_v-\gamma _vS_v- \frac{\beta _3S_vI_h}{1+\alpha _2I_h}]+\frac{\beta _2b_h}{\mu _h}[\frac{\beta _3S_vI_h}{1+\alpha _2I_h}\\\\&-(\gamma _v+\delta _v)I_v]. \end{aligned}$$
(20)

Making use of \(S^0_h=\frac{b_h}{\mu _h}\) and \(S^0_v=\frac{b_v}{\gamma _v}\) in equation (20), and taking some arrangements, we get

$$\begin{aligned} L'(t)= & {} -\mu _h (\gamma _v+\delta _v)\frac{(S_h-S^0_h)^2}{S_h} -\gamma _v \frac{\beta _2b_h}{\mu _h}\frac{(S_v-S^0_v)^2}{S_v}\\\\&-(\gamma _v+\delta _v)(\mu _h+\delta _h+\gamma _h)\alpha _2\frac{{I_{h}}^2}{1+\alpha _2I_h}\\\\&-\frac{(\gamma _v+\delta _v)\beta _2b_h\alpha _1}{\mu _h}\frac{{I_{v}}^2}{1+\alpha _1I_v}-\frac{I_h}{1+\alpha _2I_h}(\gamma +\delta _v)(\mu _h+\delta _h+\gamma _h)(1-R_0). \qquad \quad \end{aligned}$$
(21)

\(L'(t)\) is negative if \(R_0 < 1\) and \(L'(t)=0\) if \(S_h=S^0_h\), \(S_v=S^0_v\), \(I_h= I_v=0\). Hence, the largest compact invariant set \({(S_h, I_h, R_h, S_v, I_v)\in \Pi : L'(t)=0}\) is the singleton set \(E_0\), where \(E_0\) is the disease free equilibrium. Thus, by Principle [25], \(E_0\) is globally asymptotically stable in \(\Pi \). \(\square \)

To prove that the endemic equilibrium point \(E_1\) is globally asymptotically stable, we reduce the system (9), by using \(R_h=N_h-S_h-I_h\) in first equation of the system (9) and \(S_v=\frac{b_v-(\gamma _v+\delta _v)I_v}{\gamma _v}\) in fifth equation of the system (9), we obtain the following reduced system:

$$\begin{aligned} \frac{dS_h}{dt}= & {} b_h-\mu _h S_h-S_h\left( \frac{\beta _2 I_v}{1+\alpha _1 I_v}+\frac{\beta _1 I_h}{1+\alpha _2 I_h}\right) +\lambda _h (N_{h}-S_{h} -I_h),\nonumber \\ \frac{dI_h}{dt}= & {} S_h\left( \frac{\beta _2 I_v}{1+\alpha _1 I_v}+\frac{\beta _1 I_h}{1+\alpha _2 I_h}\right) -(\mu _h+\delta _h+\gamma _{h})I_{h},\nonumber \\ \frac{dI_v}{dt}= & {} \frac{\beta _3 I_h(b_v-(\gamma _v+\delta _v)I_v)}{\gamma _v(1+\alpha _2 I_h)}-(\gamma _v+\delta _v)I_v, \end{aligned}$$
(22)

subject to nonnegative initial conditions

$$\begin{aligned} S_h=S_h(0)\ge 0,~ I_h = I_h(0)\ge 0, \quad I_v = I_v(0)\ge 0. \end{aligned}$$

The endemic equilibrium of the system (22) is denoted by \(E_2\).

To prove the global stability of the endemic equilibrium, we first give the following lemma.

Lemma

If the model \(\frac{dx}{dt} = g (x)\), where \(g : D \longrightarrow R^n\), posses a unique equilibrium \(x^*\) and also a compact absorbing set exists for \(x^*\), then \(x^*\) is stable globally asymptotically given that the function P(x) and a Lozinskii measure \(\ell \) exist such that \(q= limit_{t\longrightarrow \infty }\) sup \(sup_{x}\frac{1}{t}\int ^{t}_{0}\ell (B(x(s,x)))ds<0\) [26]. The symbols P, \(\ell \) and B will stated in the following result.

Theorem 4.2

If \(R_0>1\), then the system (22) is globally asymptotically stable at \(E_2\).

Proof

At \(E_2\), the Jacobian matrix \(J(E_2)\) is given by

$$\begin{aligned} J(E_2)=\left( \begin{array}{ccc} -\mu _h-\frac{\beta _2 I_v}{1+\alpha _1 I_v}-\frac{\beta _1 I_h}{1+\alpha _2 I_h}-\lambda _h &{} -\frac{\beta _1 S_h}{(1+\alpha _2 I_h)^{2}}-\lambda _h &{} -\frac{\beta _2 S_h}{(1+\alpha _1 I_v)^{2}} \\ \frac{\beta _2 I_v}{1+\alpha _1 I_v}+\frac{\beta _1 I_h}{1+\alpha _2 I_h} &{} \frac{\beta _1 S_h}{(1+\alpha _2 I_h)^{2}}-(\mu _h+\delta _h+\gamma _h) &{} \frac{\beta _2 S_h}{(1+\alpha _1 I_v)^{2}}\\ 0&{} \frac{\beta _3 (b_v-(\gamma _v+\delta _v)I_v)}{\gamma _v(1+\alpha _2 I_h)^{2}} &{} -\frac{\beta _3 I_h(\gamma _v+\delta _v)}{\gamma _v(1+\alpha _2 I_h)}-(\gamma _v+\delta _v) \\ \end{array} \right) . \end{aligned}$$

The second additive compound matrix of \(J(E_2)\) is denoted by \(J^{[2]}\) given by

$$\begin{aligned} J^{[2]}=\left( \begin{array}{ccc} A_{11} &{} \frac{\beta _2 S_h}{(1+\alpha _1 I_v)^2} &{} \frac{\beta _2 S_h}{(1+\alpha _1 I_v)^2}\\ \frac{\beta _3 (b_v-(\gamma _v+\delta _v)I_v)}{\gamma _v(1+\alpha _2 I_h)^{2}} &{} A_{22} &{} -\frac{\beta _1 S_h}{(1+\alpha _2 I_h)^{2}}-\lambda _h\\ 0 &{} \frac{\beta _2 I_v}{1+\alpha _1 I_v}+\frac{\beta _1 I_h}{1+\alpha _2 I_h} &{} A_{33}\\ \end{array} \right) , \end{aligned}$$

where

$$\begin{aligned} A_{11}= & {} -\mu _h-\lambda _h- \frac{\beta _2 I_v}{1+\alpha _1 I_v}-\frac{\beta _1 I_h}{1+\alpha _2 I_h}+\frac{\beta _1 S_h}{(1+\alpha _2 I_h)^{2}}- (\mu _h+\delta _h+\gamma _h),\nonumber \\ A_{22}= & {} -\mu _h-\lambda _h- \frac{\beta _2 I_v}{1+\alpha _1 I_v}-\frac{\beta _1 I_h}{1+\alpha _2 I_h}-\frac{\beta _3(\gamma _v+\delta _v)I_h}{\gamma _v(1+\alpha _2 I_h)}-(\gamma _v+\delta _v),\nonumber \\ A_{33}= & {} \frac{\beta _1 S_h}{(1+\alpha _2 I_h)^{2}}-P_2-\frac{\beta _3(\gamma _v+\delta _v)I_h}{\gamma _v (1+\alpha _2 I_h)}-(\gamma _v+\delta _v), \end{aligned}$$
(23)

Consider the function

$$\begin{aligned} P= & {} P({S_h},{I_h},{I_v})=diag\bigg (1,\frac{{I_h}}{{I_v}},\frac{{I_h}}{{I_v}}\bigg ) \end{aligned}$$
(24)

with \(P^{-1}\) is

$$\begin{aligned} P^{-1}=diag\bigg (1,\frac{{I_v}}{{I_h}},\frac{{I_v}}{{I_h}}\bigg ). \end{aligned}$$

And

$$\begin{aligned} P_{f}=diag\left( 0,\frac{{I_v}{I'_{h}}-{I'_v}{I_h}}{{{I_v}}^{2}}, \frac{{I_v}{I'_{h}}-{I'_v}{I_h}}{{{I_v}}^{2}}\right) . \end{aligned}$$

\(P_{f}P^{-1}\) is

$$\begin{aligned} P_fP^{-1}=diag\left( 0,\frac{{{I'_{h}}}}{{I_h}}-\frac{{{I'_{v}}}}{{I_v}}, \frac{{{I'_{h}}}}{{I_h}}-\frac{{{I'_{v}}}}{{I_v}}\right) , \end{aligned}$$

And \(P_{f}J^{[2]}P^{-1}\) is

$$\begin{aligned} PJ^{[2]}P^{-1}=\left( \begin{array}{ccc} A_{11} &{} \frac{\beta _2 S_h}{(1+\alpha _1 I_v)^2}\frac{I_v}{I_h} &{} \frac{\beta _2 S_h}{(1+\alpha _1 I_v)^2}\frac{I_v}{I_h} \\ \\ \frac{\beta _3 (b_v-(\gamma _v+\delta _v)I_v)}{\gamma _v(1+\alpha _2 I_h)^{2}} \frac{I_h}{I_v}&{} A_{22} &{} -\frac{\beta _1 S_h}{(1+\alpha _2 I_h)^{2}}-\lambda _h \\ \\ 0 &{} \frac{\beta _2 I_v}{1+\alpha _1 I_v}+\frac{\beta _1 I_h}{1+\alpha _2 I_h} &{} A_{33}\\ \\ \end{array} \right) . \end{aligned}$$

So, we write

$$\begin{aligned} {B}=P_f P^{-1}+PJ^{[2]}P^{-1}=\left( \begin{array}{cc} {B_{11}} &{}\quad {B_{12}} \\ {B_{21}} &{}\quad {B_{22}} \\ \end{array} \right) , \end{aligned}$$

where

$$\begin{aligned} B_{11}= & {} -\mu _h-\lambda _h- \frac{\beta _2 I_v}{1+\alpha _1 I_v}-\frac{\beta _1 I_h}{1+\alpha _2 I_h}+\frac{\beta _1 S_h}{(1+\alpha _2 I_h)^{2}}-(\mu _h+\delta _h+\gamma _h),\\ B_{12}= & {} \max \left\{ \frac{\beta _2 S_h}{(1+\alpha _1 I_v)^{2}}\frac{I_v}{I_h},~\frac{\beta _2 S_h}{(1+\alpha _1 I_v)^{2}}\frac{I_v}{I_h}\right\} ,\\ B_{21}= & {} \left( \frac{I_h}{I_v}\frac{\beta _3(b_v-(\gamma _v+\delta _v)I_v)}{\gamma _v(1+\alpha _2 I_h)^{2}},0\right) ^{T},\\ B_{22}= & {} \left( \begin{array}{cc} T_{11}&{} T_{12}\\ T_{21}&{} T_{22} \end{array} \right) , \end{aligned}$$

where

$$\begin{aligned} T_{11}= & {} \frac{I'_h}{I_h}-\frac{I'_v}{I_v}-\mu _h-\lambda _h-\frac{\beta _2 I_v}{1+\alpha _1 I_v}-\frac{\beta _1 I_h}{1+\alpha _2 I_h} -\frac{\beta _3(\gamma _v+\delta _v)I_h}{\gamma _v(1+\alpha _2 I_h)}-(\gamma _v+\delta _v),\\\\T_{12}= & {} -\frac{\beta _1 S_h}{(1+\alpha _2 I_h)^{2}}-\lambda _h,\\\\T_{21}= & {} \frac{\beta _2 I_v}{1+\alpha _1 I_v}+\frac{\beta _1 I_h}{1+\alpha _2 I_h},\\ T_{22}= & {} \frac{I'_h}{I_h}-\frac{I'_v}{I_v}+\frac{\beta _1 S_h}{(1+\alpha _2 I_h)^{2}}-\frac{\beta _3(\gamma _v+\delta _v)I_h}{\gamma _v(1+\alpha _2 I_h)}-(\gamma _v+\delta _v)-(\mu _h+\delta _h+\gamma _h). \end{aligned}$$

Suppose the vector \((\hat{u},\hat{v},\hat{w})\) in \(R^{3}\) and its norm ||.|| will be defined as

$$\begin{aligned} ||(\hat{u},\hat{v},\hat{w})||=max\{|\hat{u}|,|\hat{v}|+|\hat{w}|\}. \end{aligned}$$

Suppose \(\mu {B}\) represent Lozinski measure with the above defined norm. So as described in [26], we choose

$$\begin{aligned} \mu ({B})\le \sup (g_1,~g_2), \end{aligned}$$

where

$$\begin{aligned} g_1= & {} \mu ({B_{11}})+{|B_{12}|},\quad g_2=|{B_{21}}|+\mu ({B_{22}}), \end{aligned}$$

\(|{B_{21}}|\) and \({|B_{12}|}\) are the matrix norm associated with vector \(\ell \) and \(\mu \) represent the Lozinski measure with respect to \(\ell \) norm, then

$$\begin{aligned} \mu (B_{11})= & {} -\mu _h-\lambda _h- \frac{\beta _2 I_v}{1+\alpha _1 I_v}-\frac{\beta _1 I_h}{1+\alpha _2 I_h}+\frac{\beta _1 S_h}{(1+\alpha _2 I_h)^{2}}-(\mu _h+\delta _h+\gamma _h),\\\\|B_{12}|= & {} \max \bigg \{\frac{\beta _2 S_h}{(1+\alpha _1 I_v)^{2}}\frac{I_v}{I_h},~\frac{\beta _2 S_h}{(1+\alpha _1 I_v)^{2}}\frac{I_v}{I_h}\bigg \}, \end{aligned}$$
(25)

Therefore,

$$\begin{aligned} g_1= & {} \mu (B_{11})+|B_{12}|\\\\= & {} -\mu _h-\lambda _h- \frac{\beta _2 I_v}{1+\alpha _1 I_v}-\frac{\beta _1 I_h}{1+\alpha _2 I_h}+\frac{\beta _1 S_h}{(1+\alpha _2 I_h)^{2}}+\frac{\beta _2 S_h}{(1+\alpha _1 I_v)^{2}}\frac{I_v}{I_h}-(\mu _h+\delta _h+\gamma _h),\\\\\le & {} -\mu _h-\lambda _h- \frac{\beta _2 I_v}{1+\alpha _1 I_v}-\frac{\beta _1 I_h}{1+\alpha _2 I_h}+\frac{\beta _1 S_h}{(1+\alpha _2 I_h)}+\frac{\beta _2 S_h}{(1+\alpha _1 I_v)}\frac{I_v}{I_h}-(\mu _h+\delta _h+\gamma _h),\\\\\le & {} \frac{I'_h}{I_h}-\mu _h-\lambda _h-\frac{\beta _2 I_v}{1+\alpha _1 I_v}-\frac{\beta _1 I_h}{1+\alpha _2 I_h}, \end{aligned}$$

using system (22),

$$\begin{aligned} \frac{I'_h}{I_h}= & {} \frac{I_v}{I_h}\frac{\beta _2 S_h}{(1+\alpha _1 I_v)}+{\frac{\beta _1 S_h}{1+\alpha _2 I_h}}-(\mu _h+\delta _h+\gamma _h), \end{aligned}$$

we get

$$\begin{aligned} g_1\le & {} \frac{I'_h}{I_h}-\mu _h-\lambda _h-\frac{\beta _2 I_v}{1+\alpha _1 I_v}-\frac{\beta _1 I_h}{1+\alpha _2 I_h}. \end{aligned}$$

Again

$$\begin{aligned} |B_{21}|= & {} \frac{I_h}{I_v}\frac{\beta _3(b_v-(\gamma _v +\delta _v)I_v)}{\gamma _v(1+\alpha _2 I_h)^{2}}, \end{aligned}$$
$$\begin{aligned} \mu (B_{22})= & {} Sup\Big \{\frac{I'_h}{I_h}-\frac{I'_v}{I_v}-\mu _h-\lambda _h-\frac{\beta _2 I_v}{1+\alpha _1 I_v}-\frac{\beta _1 I_h}{1+\alpha _2 I_h} -\frac{\beta _3(\gamma _v+\delta _v)I_h}{\gamma _v(1+\alpha _2 I_h)}\\\\&-(\gamma _v+\delta _v)+\frac{\beta _2 I_v}{1+\alpha _1 I_v}+\frac{\beta _1 I_h}{1+\alpha _2 I_h},~~ \frac{I'_h}{I_h}-\frac{I'_v}{I_v}+\frac{\beta _1 S_h}{(1+\alpha _2 I_h)^{2}}-\frac{\beta _3(\gamma _v+\delta _v)I_h}{\gamma _v(1+\alpha _2 I_h)}\\\\&-(\gamma _v+\delta _v)-(\mu _h+\delta _h+\gamma _h) -\frac{\beta _1 S_h}{(1+\alpha _2 I_h)^{2}}-\lambda _h\Big \},\\\\= & {} \frac{I'_h}{I_h}-\frac{I'_v}{I_v}-\mu _h-\lambda _h-(\gamma _v+\delta _v)-\frac{\beta _3(\gamma _v+\delta _v)I_h}{\gamma _v(1+\alpha _2 I_h)}-(\mu _h+\delta _h+\gamma _h)-\lambda _h. \end{aligned}$$

So

$$\begin{aligned} g_2= & {} \mu ({B_{22}})+|{B_{21}}|,\\= & {} \frac{I'_h}{I_h}-\frac{I'_v}{I_v}-\mu _h-\lambda _h-(\gamma _v+\delta _v)-\frac{\beta _3(\gamma _v+\delta _v)I_h}{\gamma _v(1+\alpha _2 I_h)}\\&-(\mu _h+\delta _h+\gamma _h)-\lambda _h+\frac{I_h}{I_v}\frac{\beta _3(b_v-(\gamma _v+\delta _v)I_v)}{\gamma _v(1+\alpha _2 I_h)^{2}},\\\le & {} \frac{I'_h}{I_h}-\frac{I'_v}{I_v}-\mu _h-\lambda _h-(\gamma _v+\delta _v)-\frac{\beta _3(\gamma _v+\delta _v)I_h}{\gamma _v(1+\alpha _2 I_h)}\\&-(\mu _h+\delta _h+\gamma _h)-\lambda _h+\frac{I_h}{I_v}\frac{\beta _3(b_v-(\gamma _v+\delta _v)I_v)}{\gamma _v(1+\alpha _2 I_h)},\\\le & {} \frac{I'_h}{I_h}-\mu _h-\lambda _h-\frac{\beta _3(\gamma _v+\delta _v)I_h}{\gamma _v(1+\alpha _2 I_h)}-(\mu _h+\delta _h+\gamma _h)-\lambda _h, \end{aligned}$$

we used in above \(g_2\), the third equation of the system (22),

$$\begin{aligned} \frac{I'_v}{I_v}=\frac{I_h}{I_v}\frac{\beta _3(b_v-(\gamma _v+\delta _v)I_v)}{\gamma _v(1+\alpha _2 I_h)^{2}}-(\gamma _v+\delta _v). \end{aligned}$$

So,

$$\begin{aligned} \mu {B}\le \sup (g_1,g_2)\le \frac{I'_h}{I_h}-\mu \end{aligned}$$

then,

$$\begin{aligned} q=\frac{1}{t}\int _{0}^{t}\mu {B}ds\le \frac{1}{t}\int _{0}^{t} \left( \frac{I'_h}{I_h}-\mu \right) ds=\frac{1}{t}ln\frac{I_h(t)}{I_h(0)}-\mu . \end{aligned}$$

Implies that \(q\le -\frac{\mu }{2}<0\). Thus the result [27], implies that the positive equilibrium point \(E_2\) of the system (22) is globally asymptotically stable. \(\square \)

Table 1 Parameter values used in numerical simulation
Full size table
Fig. 2
figure 2

Population behavior of human

Full size image
Fig. 3
figure 3

Population behavior of vector

Full size image
Fig. 4
figure 4

Represents the graph of susceptible human with the effect of \(\alpha _1\) and \(\alpha _2\) with the parameters \(\mu _h= 0.31\), \(b_h=099\), \(\alpha 1=0.83\), \(\alpha 2=0.083\), \(\delta _v=0.32\), \(\beta _1= 0.91\), \(b_v=290\), \(\gamma _h= 0.71\), \(\gamma _v=0.8\), \(\beta _3=0.22\), \(\delta _h=0.61\), \(\lambda _h=0.71\), \(\beta _2=0.92\)

Full size image
Fig. 5
figure 5

Represents the graph of infected human with the effect of \(\alpha _1\) and \(\alpha _2\) with the parameters \(\mu _h= 0.31\), \(b_h=099\), \(\beta _2=0.92\), \(\alpha 1=0.83\), \(\alpha 2=0.083\), \(\beta _1= 0.91\), \(\delta _v=0.32\), \(b_v=290\), \(\gamma _h= 0.71\), \(\gamma _v=0.8\), \(\beta _3=0.22\), \(\delta _h=0.61\), \(\lambda _h=0.71\)

Full size image
Fig. 6
figure 6

Represents the graph of recovered human with the effect of \(\alpha _1\) and \(\alpha _2\) with the parameters \(\mu _h= 0.31\), \(b_h=099\), \(\beta _1= 0.91\), \(\alpha 1=0.83\), \(\alpha 22=0.083\), \(\delta _v=0.32\), \(b_v=290\), \(\gamma _h= 0.71\), \(\beta _3=0.22\), \(\gamma _v=0.8\), \(\beta _2=0.92\), \(\delta _h=0.61\), \(\lambda _h=0.71\)

Full size image
Fig. 7
figure 7

Represents the graph of susceptible vector with the effect of \(\alpha _1\) and \(\alpha _2\) with the parameters \(\mu _h= 0.31\), \(b_h=099\), \(\alpha 1=0.83\), \(\beta _3=0.22\), \(\alpha 2=0.083\), \(\delta _v=0.32\), \(\beta _1= 0.91\), \(b_v=290\), \(\gamma _h= 0.71\), \(\gamma _v=0.8\), \(\beta _2=0.92\), \(\delta _h=0.61\), \(\lambda _h=0.71\)

Full size image
Fig. 8
figure 8

Represents the graph of susceptible vector with the effect of \(\alpha _1\) and \(\alpha _2\) with the parameters \(\mu _h= 0.31\), \(b_h=099\),\(\alpha 1=0.83\), \(\beta _3=0.22\), \(\alpha 2=0.083\), \(\delta _v=0.32\), \(b_v=290\), \(\gamma _h= 0.71\), \(\gamma _v=0.8\), \(\beta _1= 0.91\), \(\delta _h=0.61\), \(\lambda _h=0.71\), \(\beta _2=0.92\)

Full size image

Numerical Simulations

In this section, we present the numerical solution of the system (9). The parameter values used in the numerical solution are shown in Table 1. Figures 2 and 3 shows the population behavior of human and vector population respectively. Figures 4, 5, 6, 7 and 8 represents Susceptible human, infected human, recovered human, susceptible vector and infected vector with the parameters \(\alpha _1\) and \(\alpha _2\). Figure 2 represent the human population, the dashed line represent the behavior of susceptible human, the bold line shows the population behavior of infected individuals, the dot dashed line shows the population behavior of recovered human. Figure 3 shows the population of behavior of vector, the susceptible vector is represented by bold line and the dashed line shows the population of infected vector. The plot shows the susceptible human population with saturation effect for the values of \(\alpha _1\) and \(\alpha _2\) in Fig. 4. The graph of susceptible human decreases with the saturated effect, for the values of \(\alpha _1=0.83\) and \(\alpha _2=0.83\). The dotted line shows the population of susceptible human without saturation effect and the dashed line shows the saturation effect of human and the saturation effect of vector is represented by a dot dashed line. Due the effect of \(\alpha _1\) and \(\alpha _2\) the population of susceptible individuals change sharply. The plot shows the infected human population with the saturated effect of the values \(\alpha _1\) and \(\alpha _2\) in Fig. 5. The graph of infected human decreases with the saturated effect, for the values of \(\alpha _1=0.83\) and \(\alpha _2=0.83\). The dotted line shows the population of infected human without saturated effect and the dashed line shows the saturated effect. Due the effect of \(\alpha _1\) and \(\alpha _2\) the population of infected individuals changes. The plot shows the recovered human population with saturated effect for the values of \(\alpha _1\) and \(\alpha _2\) in Fig. 6. The graph of recovered human decreases with the saturated effect, for the values for \(\alpha _1=0.83\) and \(\alpha _2=0.83\). The dotted line shows the population of recovered human without saturated effect and the dashed line shows the saturated effect of human and the saturated effect of vector is represented by a dot dashed line. Due the effect of \(\alpha _1\) and \(\alpha _2\) the population of recovered individuals increases. The plot shows the vector population with saturated effect for the values of \(\alpha _1\) and \(\alpha _2\) in Fig. 7. The graph of susceptible vector decreases with the saturated infection rate, for the values for \(\alpha _1=0.83\) and \(\alpha _2=0.83\). The dotted line shows the population of susceptible human without saturated effect and the dashed line shows the saturated effect of human and the saturated effect of vector is represented by a dot dashed line. Due the effect of \(\alpha _1\) and \(\alpha _2\) the population of susceptible individuals decreases. The plot shows the infected vector population with the effect of \(\alpha _1\) and \(\alpha _2\) in Fig. 8. The graph of infected vector decreases with the with the saturation factor \(\alpha _1=0.83\) and \(\alpha _2=0.83\). The dotted line shows the population of infected vector without saturation effect and the dashed line shows the saturation effect of human and the saturated parameter effect of vector is represented by a dot dashed line. Due the effect of \(\alpha _1\) and \(\alpha _2\) the population of infected vector decreases. The suggested parameters \(\alpha _1=0.83\) and \(\alpha _2=0.83\) can reduce the infection in the leptospirosis disease interaction with human.

Conclusion

The dynamic behavior of leptospirosis disease with saturated incidence has been presented successfully. The mathematical results obtained with their mathematical interpretation. The stability of the disease free and endemic equilibrium is completely described by the basic reproduction number \(R_0\). We found, when \(R_0 < 1\), the disease free equilibrium at \(E_0\) is stable locally as well as globally. Further, the endemic equilibrium is obtained. We obtained that, when \(R_0>1\), the endemic equilibrium is stable both locally and globally. Moreover, the numerical results for the model is obtained and briefly discussed. The parameters \(\alpha _1\) and \(\alpha _2\) effect have been discussed in numerical solution.