Nonlinear Vibration Analysis of Sigmoid Functionally Graded Sandwich Plate with Ceramic-FGM-Metal Layers

Abstract

Purpose

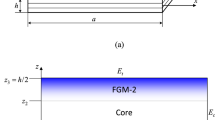
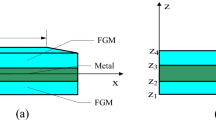
In the present study, free and forced nonlinear vibration characteristics of a sandwich functionally graded material (FGM) plate resting on Pasternak elastic foundation have been investigated. The formulation is based on non-polynomial higher-order shear deformation theory with inverse hyperbolic shape function. A new modified sigmoid law is presented to compute the effective material properties of sandwich FGM plate.

Methods

The governing equilibrium equations have been formulated using Hamilton’s principle and the governing nonlinear coupled ordinary differential equations are derived using stress function method in conjunction with Galerkin approach. The resulting equations are then solved using fourth order Runge–Kutta time integration scheme for simply supported plate with immovable edges.

Results

Comprehensive parametric studies have been performed to analyze the influence of geometric configuration, volume fraction exponent, and elastic medium parameter on nonlinear time series analysis for different configurations of sandwich plate. A nonlinear complex behaviour of the plate is studied using time displacement response, phase-plane plot and Poincaré map.

Conclusion

For Pasternak foundation, system shows multi-loop periodic nature while it losses its periodicity and shows the quasi-periodic nature for Winkler foundation. In addition, it has been observed that the system shows quasi-periodic route to chaotic nature for thick plate to thin plate.

Appendix

$$\begin{aligned} \kappa_{11} &= \frac{1}{{1 - \nu^{2} }}\left( {\frac{{B^{2} }}{A} - D} \right)\left( {\alpha^{2} + \beta^{2} } \right)^{2} - K_{w} - K_{p} \left( {\alpha^{2} + \beta^{2} } \right) \hfill \\ \kappa_{12}& = - \frac{\alpha }{{1 - \nu^{2} }}\left( {\frac{BF}{A} + \frac{{B^{2} \vartheta }}{A} - \left( {D\vartheta + H} \right)} \right)\left( {\alpha^{2} + \beta^{2} } \right) \hfill \\ \kappa_{13}& = - \frac{\beta }{{1 - \nu^{2} }}\left( {\frac{BF}{A} + \frac{{B^{2} \vartheta }}{A} - \left( {D\vartheta + H} \right)} \right)\left( {\alpha^{2} + \beta^{2} } \right) \hfill \\ \kappa_{nl}& = - \frac{A}{16}\left( {\alpha^{4} + \beta^{4} } \right),\,\,\psi_{11} = N_{{x_{0} }} \alpha^{2} + N_{{y_{0} }} \beta^{2} , \hfill \\ \end{aligned}$$

$$\begin{aligned} \kappa_{21}& = - \frac{\alpha }{{1 - \nu^{2} }}\left( {\frac{BF}{A} + \frac{{B^{2} \vartheta }}{A} - \left( {D\vartheta + H} \right)} \right)\left( {\alpha^{2} + \beta^{2} } \right) \hfill \\ \kappa_{22} &= - \left[ \left( {\frac{{\alpha^{2} }}{{1 - \nu^{2} }} + \frac{{\beta^{2} }}{{2\left( {1 + \nu } \right)}}} \right)\left( D\vartheta^{2} + 2H\vartheta \right.\right.\\ &\quad\left.\left. + J - \frac{{B^{2} \vartheta^{2} }}{A} - \frac{{F^{2} }}{A} - 2\frac{B\vartheta F}{A} \right) + \frac{1}{{2\left( {1 + \nu } \right)}}\left( {A\vartheta^{2} + 2\vartheta K + L} \right) \right] \hfill \\ \kappa_{23}& = - \frac{\alpha \beta }{{2\left( {1 - \nu } \right)}}\left( {D\vartheta^{2} + 2H\vartheta + J - \frac{{B^{2} \vartheta^{2} }}{A} - \frac{{F^{2} }}{A} - 2\frac{B\vartheta F}{A}} \right), \hfill \\ \end{aligned}$$

$$\begin{aligned} \kappa_{31} &= - \frac{\beta }{{1 - \nu^{2} }}\left( {\frac{BF}{A} + \frac{{B^{2} \vartheta }}{A} - \left( {D\vartheta + H} \right)} \right)\left( {\alpha^{2} + \beta^{2} } \right) \hfill \\ \kappa_{32}& = - \frac{\alpha \beta }{{2\left( {1 - \nu } \right)}}\left( {D\vartheta^{2} + 2H\vartheta + J - \frac{{B^{2} \vartheta^{2} }}{A} - \frac{{F^{2} }}{A} - 2\frac{B\vartheta F}{A}} \right) \hfill \\ \kappa_{33}& = - \left[ \left( {\frac{{\beta^{2} }}{{1 - \nu^{2} }} + \frac{{\alpha^{2} }}{{2\left( {1 + \nu } \right)}}} \right)\left( D\vartheta^{2} + 2H\vartheta + J - \frac{{B^{2} \vartheta^{2} }}{A}\right.\right.\\ &\quad\left.\left. - \frac{{F^{2} }}{A} - 2\frac{B\vartheta F}{A} \right) + \frac{1}{{2\left( {1 + \nu } \right)}}\left( {A\vartheta^{2} + 2\vartheta K + L} \right) \right], \hfill \\ \end{aligned}$$

$$\begin{aligned} M_{11} &= \left( {\frac{{I_{1}^{2} }}{{I_{0} }} - I_{2} } \right)\left( {\alpha^{2} + \beta^{2} } \right) - I_{0} \quad M_{21} = \alpha \left( {J_{2} - \frac{{I_{1} J_{1} }}{{I_{0} }}} \right) \\ M_{31} &= \beta \left( {J_{2} - \frac{{I_{1} J_{1} }}{{I_{0} }}} \right) \hfill \\ M_{12}& = \alpha \left( {J_{2} - \frac{{I_{1} J_{1} }}{{I_{0} }}} \right)\quad M_{22} = \left( {\frac{{J_{1}^{2} }}{{I_{0} }} - J_{3} } \right) \quad M_{32} = 0 \hfill\\ M_{13} & = \beta \left( {J_{2} - \frac{{I_{1} J_{1} }}{{I_{0} }}} \right) \quad M_{23} = 0 \quad M_{33} = \left( {\frac{{J_{1}^{2} }}{{I_{0} }} - J_{3} } \right), \hfill \\ \end{aligned}$$

$$\begin{aligned} \tilde{\tilde{\kappa }}_{11} &= \frac{{\alpha \left( {\left( { - 1} \right)^{m} - 1} \right)\left( {\left( { - 1} \right)^{n} - 1} \right)}}{{\pi^{2} mn\left( {1 - \nu^{2} } \right)}}\left( {B\vartheta + F} \right)\left( {\alpha^{2} + \nu \beta^{2} } \right),\\ \tilde{\tilde{\kappa }}_{12} &= \frac{{\beta \left( {\left( { - 1} \right)^{m} - 1} \right)\left( {\left( { - 1} \right)^{n} - 1} \right)}}{{\pi^{2} mn\left( {1 - \nu^{2} } \right)}}\left( {B\vartheta + F} \right)\left( {\nu \alpha^{2} + \beta^{2} } \right) \hfill \\ \tilde{\tilde{\kappa }}_{13} &= - \frac{{B\left( {\left( { - 1} \right)^{m} - 1} \right)\left( {\left( { - 1} \right)^{n} - 1} \right)}}{{\pi^{2} mn\left( {1 - \nu^{2} } \right)}}\left( {\alpha^{4} + 2\nu \alpha^{2} \beta^{2} + \beta^{4} } \right),\\ \tilde{\tilde{\tilde{\kappa }}}& = \left( {\kappa_{nl} - \frac{A}{{8\left( {1 - \nu^{2} } \right)}}\left( {\alpha^{4} + 2\nu \alpha^{2} \beta^{2} + \beta^{4} } \right)} \right). \hfill \\ \end{aligned}$$