1 Introduction

Concrete which is one of the major construction material has been plagued recently by high cost of the conventional constituent materials namely; cement, fine and coarse aggregate and water. This economic implications has made several researchers to utilize and incorporate supplementary cementious materials (SCM) in concrete. The SCMs are majorly derived from solid wastes which help in recycling and re-use of the waste [1]. In the quest to achieve renewable and sustainable materials, biological and agricultural wastes such as periwinkle shell ash, oyster shell ash, wood ash, corncob ash have been utilized as SCM in concrete infrastructures [2,3,4,5]. Incorporating these materials in the construction of infrastructures reduces cost of construction materials, alleviates environmental issues during cement production and reduces amount of solid discarded into the environment, thereby promoting the concrete’s characteristic behaviour by enhancing sustainability of fresh and hardened concrete [6,7,8].

The compressive strength of any material is its capacity or structure to withstand, absorb or resist compression force which is the force that squeezes material together. The concrete’s compressive strength is determined by the ability of the material to resist cracking and fissure failure. The ultimate compressive strength of a material is equal to the value of uniaxial compression stress attained at complete failure point and it depends on factors such as; compressive strength of the constituents, water-cement ratio, quality of materials, curing methods, air entrainment, temperature effects and proportion of mixture constituents. The compressive strength is one of the major engineering properties of concrete and has become a standard for industrial practise that concrete is classified based on the compressive strength (grades). It is important to note that several materials used in the construction works fracture at their compressive strength limit while some deform irreversibly; therefore, the compression load limit may be considered for a given amount of deformation. The use of rice husk ash (RHA) which is derived from solid waste and possesses high aluminosilicate content as a fifth component and not for partial replacement in concrete work is investigated in this research work. The idea in this research work is to totally integrate the pozzolanic material in the concrete mixture using statistical approach to obtain the optimum mixture combination of the five component concrete namely; cement, water fine and coarse aggregate and RHA. Using the statistical approach, Scheffe’s simplex second order regression model is generated to optimize the compressive strength property on the RHA concrete. The utilization of pozzolanic material such as RHA using statistical approach has been found to be a beneficial technique in engineering practice. In a research work carried out by Onuamah [9] laterite-RHA-water were utilized for the production of a hollow sandcrete block using Scheffe’s optimization approach. Hollow block sample of 450 mm × 225 mm × 150 mm dimension were produced and tested for strength after 28 days hydration period. The model generated was adequate when tested with student’s t test. The maximum obtainable compressive strength from the model results is 1.57 N/mm2. Also, Putra Jaya et al. [10] studied the strength characteristics of RHA under sodium sulphate attack. The durability performance of the concrete with cement partially replaced from 10 to 40% from their findings, concrete with 10 to 20% of replacements by RHA showed excellent durability performance, the results also indicated that due to the effect of the pozzolanic reaction of RHA, the amount of Ca(OH)2 in the cement-RHA concrete was lower than that of Portland cement. Furthermore, Nwakonobi and Osadebe [11] worked on the development of optimization model for proportioning mixture of clay-rice husk ash–cement mixture for animal building. It was observed that the quality of the clay soil as a building material can be improved but depends on the proper proportioning of its ingredients. The optimum value of compressive strength predicted by the generated model is 18.204 N/mm2 corresponding to 14.16, 8.04 and 77.80% of rice husk ash, cement and clay respectively.

This research study aims to utilize supplementary cementitous materials to partially replace cement portion in the concrete mixture to obtain a five component concrete mixture of water, coarse and fine aggregates, cement and rice husk ash. The main aim of this study is to obtain the optimum mix proportion for five component mixture of water, cement, rice husk ash, fine aggregate and coarse aggregate that will give the maximum compressive strength property of concrete. Generally, the concrete structures’ compressive strength is impacted by adequate proportioning of their components [12,13,14,15,16,17]. This research objective is the utilization of Scheffe’s simplex optimization approach in formulating mathematical model that would relate concrete’s compressive strength having rice husk ash as supplementary cementitious materials (SCM). This study will add to existing knowledge on optimization of concrete using SCM. The expected benefit of this study will enhance good decision making on the batching and grade of concrete that could be required for certain concrete structures.

1.1 Simplex-lattice design

Scheffe’s theory states that the factor space for mixture experiment is a regular (q − 1) dimensional simplex and for the mixture, the sum of the constituents of the mixture must sum to unity. This is expressed mathematically in Eq. (1);

$$X_{1} + X_{2} + \cdots + X_{q} = 1;\;{\text{where}}\; {0} \le X_{i} \le 1\;{\text{for}}\;i = 1,2, \ldots ,q$$
(1)

The simplex-lattice is an ordered arrangement of line joining the assumed experimental points of the mixture ingredient proportion design. Due to the sum to one constraint (Eq. 1); the representative geometry of the factor space containing the q-components consists of all points on or inside the boundaries of a regular (q − 1) dimensional simplex. The Factor space is a straight line for two mixture components q = 2; for three mixture components q = 3, the simplex factor space is an equilateral triangle. A {q, m} simplex lattice design for q factors (components) is defined by all possible combinations of component levels with the proportions being.

A simplex-lattice design of mixture with degree m consists of m + 1 points of the factor space which is equally spaced between values ranging from 0 to 1. For m = 2 which is the second order; then the fractions will be 0, 1/2, 1. For m = 3 the fraction values are 0, 1/3, 2/3, 1 giving us four points I.e. m + 1 points. However, the number of experimental trials in the optimization process is derived from the formula (Eq. 2):

$${\text{N}} = \frac{{\left( {{\text{q}} + {\text{m}} - 1} \right)!}}{{{\text{m}}!\left( {{\text{q}} - 1} \right)!}}.$$
(2)
$${\text{For}}\,{\text{a }}\,\left( {5,2} \right)\,{\text{lattice}}\,{\text{we}}\,{\text{have: }}\quad {\text{N}} = \frac{{\left( {5 + 2 - 1} \right)!}}{{2!\left( {5 - 1} \right)!}} = { }\frac{6!}{{2!4!}} = 15.$$

Since we have a five component mixture and fifteen trials, five out of the fifteen pseudo components are situated at the extreme vertices of the simplex. These five points are termed the pure or binary blends. Similarly, the remaining ten pseudo components are situated at the middle points of the adjoining line of the vertices of simplex. The fifteen pseudo component points are defined as follows; 1.[1:0:0:0:0], 2.[0:1:0:0:0], 3.[0:0:1:0:0], 4.[0:0:0:1:0], 5.[0:0:0:0:1], 6.[0.5:0.5:0:0:0], 7.[0.5:0:0.5:0:0], 8.[0.5:0:0:0.5:0], 9.[0.5:0:0:0:0.5], 10.[0:0.5:05:0:0], 11.[05:0:0:0.5:0], 12.[0:0.5:0:0:0.5], 13.[0:0:0.5:05:0], 14.[0:0:0.5:0:0.5], 15.[0:0:0:0.5:0.5].

The {5, 2} simplex lattice mixture have a factor space in the form of a three dimensional tetrahedron with five vertices and equidistant to the other; this is based on the imposed sum to one constraint (Eq. 1). This is shown in Fig. 1;

Fig. 1
figure 1

The {5, 2} simplex lattice

Full size image

Expanding Eq. (1), we get;

$$1 = X_{1} + X_{2} + X_{3} + X_{4} + X_{5}$$
(3)

Thus in the general canonical form of mixture models can be expressed mathematically as follows;

$${\text{Linear:}}\quad \eta = \sum\limits_{i = 1}^{q} {\beta_{i} x_{i} }$$
(4)
$${\text{Quadratic:}}\quad \eta = \sum\limits_{i = 1}^{q} {\beta_{i} x_{i} } + \sum\limits_{{}}^{{}} {\sum\limits_{i < j}^{q} {\beta_{ij} x_{i} } } x_{j}$$
(5)

Substituting the values of i and j in Eq. (5) the quadratic equation for \(\left( {0 \le i \le j \le 5} \right)\) transforms to

$${\text{Y}} = {\text{b}}_{{\text{o}}} + {\text{ b}}_{{1}} {\text{X}}_{{1}} + {\text{ b}}_{{2}} {\text{X}}_{{2}} + {\text{ b}}_{{3}} {\text{X}}_{{3}} + {\text{ b}}_{{4}} {\text{X}}_{{4}} + {\text{ b}}_{{5}} {\text{X}}_{{5}} + {\text{ b}}_{{{11}}} {\text{X}}_{{1}}^{{2}} + {\text{ b}}_{{{12}}} {\text{X}}_{{1}} {\text{X}}_{{2}} + {\text{ b}}_{{{13}}} {\text{X}}_{{1}} {\text{X}}_{{3}} + {\text{ b}}_{{{14}}} {\text{X}}_{{1}} {\text{X}}_{{4}} + {\text{ b}}_{{{15}}} {\text{X}}_{{1}} {\text{X}}_{{5}} + {\text{ b}}_{{{22}}} {\text{X}}_{{2}}^{{2}} + {\text{ b}}_{{{23}}} {\text{X}}_{{2}} {\text{X}}_{{3}} + {\text{ b}}_{{{24}}} {\text{X}}_{{2}} {\text{X}}_{{4}} + {\text{ b}}_{{{25}}} {\text{X}}_{{2}} {\text{X}}_{{5}} + {\text{ b}}_{{{33}}} {\text{X}}_{{3}}^{{2}} + {\text{ b}}_{{{34}}} {\text{X}}_{{3}} {\text{X}}_{{4}} + {\text{ b}}_{{{35}}} {\text{X}}_{{3}} {\text{X}}_{{5}} + {\text{ b}}_{{{44}}} {\text{X}}_{{4}}^{{2}} + {\text{ b}}_{{{45}}} {\text{X}}_{{4}} {\text{X}}_{{5}} + {\text{ b}}_{{{55}}} {\text{X}}_{{5}}^{{2}}$$
(6)

Thus, multiplying Eq. (3) by bo yields Eq. (7) below;

$$b_{0} = b_{0} X_{1} + b_{0} X_{2} + b_{0} X_{3} + b_{0} X_{4} + b_{0} X_{5}$$
(7)

The Xi parameter is successively multiplied with Eq. (3) to get Eq. (8)

$$\begin{aligned} & X_{1} - X_{1} X_{2} - X_{1} X_{3} - X_{1} X_{4} - X_{1} X_{5} = X_{1}^{2} \\ & X_{2} - X_{1} X_{2} - X_{2} X_{3} - X_{2} X_{4} - X_{2} X_{5} = X_{2}^{2} \\ & X_{3} - X_{1} X_{3} - X_{2} X_{3} - X_{3} X_{4} - X_{3} X_{5} = X_{3}^{2} \\ & X_{4} - X_{1} X_{4} - X_{2} X_{4} - X_{3} X_{4} - X_{4} X_{5} = X_{4}^{2} \\ & X_{5} - X_{1} X_{5} - X_{2} X_{5} - X_{3} X_{5} - X_{4} X_{5} = X_{5}^{2} \\ \end{aligned}$$
(8)

Substituting Eqs. (7) and (8) into Eq. (6) yields;

$$Y = \beta_{1} X_{1} + \beta_{2} X_{2} + \beta_{3} X_{3} + \beta_{4} X_{4} + \beta_{5} X_{5} + \beta_{12} X_{1} X_{2} + \beta_{13} X_{1} X_{3} + \beta_{14} X_{1} X_{4} + \beta_{15} X_{1} X_{5} + \beta_{23} X_{2} X_{3} + \beta_{24} X_{2} X_{4} + \beta_{25} X_{2} X_{5} + \beta_{34} X_{3} X_{4} + \beta_{35} X_{3} X_{5 + z} + \beta_{45} X_{4} X_{5}$$
(9)

The mathematical relationship between the actual response and Scheffe’s regression coefficients is expressed in Eq. (10)

$$\begin{aligned} & Y_{1} = \beta_{1,} Y_{2} = \beta_{2, } Y_{3} = \beta_{3} , Y_{4} = \beta_{4} ,Y_{5} = \beta_{5} , \beta_{12} = 4Y_{12} - 2Y_{1} - 2Y_{2,} \beta_{13} \\ & \quad \quad = 4Y_{13} - 2Y_{1} - 2Y_{3} ,\beta_{14} = 4Y_{14} - 2Y_{1} - 2Y_{4} ,\beta_{15} = 4Y_{15} - 2Y_{1} - 2Y_{5} ,\beta_{23} \\ & \quad \quad = 4Y_{23} - 2Y_{2} - 2Y_{3} , \beta_{24} = 4Y_{24} - 2Y_{2} - 2Y_{4} ,\beta_{25} = 4Y_{25} - 2Y_{2} - 2Y_{5} ,\beta_{34} \\ & \quad \quad = 4Y_{34} - 2Y_{3} - 2Y_{4} ,\beta_{35} = 4Y_{35} - 2Y_{3} - 2Y_{5} , \beta_{45} \\ & \quad \quad = 4Y_{45} - 2Y_{4} - 2Y_{5} \\ \end{aligned}$$
(10)

1.2 Pseudo and real components

The relationship between the real or actual and pseudo components is expressed mathematically in Eq. (11)

$$AX = AZ$$
(11)

where Z is the real components, X is for the pseudo components and A is a constant representing the pure or binary blends and also the initial mixture proportion ratio which will be chosen by the decision maker based on deep experience in concrete mixture experiments. This initial trial mix generates the matrix A which is shown as shown below;

$$\begin{aligned} & {\text{Z}}_{{1}} \left[ {0.{5}0:0.{9}0:{1}.{2}0:{1}.{4}0:0.{1}0} \right],{\text{ Z}}_{{2}} \left[ {0.{55}:0.{75}:{1}.{25}:{1}.{5}0:0.{25}} \right],{\text{ Z}}_{{3}} \left[ {0.{6}0:0.{65}:{1}.{3}0:{1}.{6}0:0.{35}} \right], \\ & \;{\text{Z}}_{{4}} \left[ {0.{65}:0.{6}0:{1}.{35}:{1}.{7}0:0.{4}0} \right]{\text{ and Z}}_{{5}} \left[ {0.{6}0:0.{5}0:{1}.{4}0:{1}.{8}0:0.{5}0} \right] \\ \end{aligned}$$

Putting these into a matrix form, we have [A] matrix:

$$\left( {\begin{array}{*{20}c} {0.50} & {0.55} & {0.60} & {0.65} & {0.60} \\ {0.90} & {0.75} & {0.65} & {0.60} & {0.50} \\ {1.20} & {1.25} & {1.30} & {1.35} & {1.40} \\ {1.40} & {1.50} & {1.60} & {1.70} & {1.80} \\ {0.10} & {0.25} & {0.35} & {0.40} & {0.50} \\ \end{array} } \right)$$

The corresponding pseudo component for this initial mix since it is situated at the vertices of the tetrahedron is a binary blend. The corresponding pseudo components is used to determine the corresponding actual mixture components, where X1 = water cement ratio fraction, X2 = Portland limestone cement fraction, X3 = fine aggregate fraction, X4 = coarse aggregate and X5 = fraction of rice husk ash fraction.

For \({\text{A}}_{12} ;\)

$$\left( {\begin{array}{*{20}c} {Z_{1} } \\ {Z_{2} } \\ {Z_{3} } \\ {Z_{4} } \\ {Z_{5} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {0.50} & {0.55} & {0.60} & {0.65} & {0.60} \\ {0.90} & {0.75} & {0.65} & {0.60} & {0.50} \\ {1.20} & {1.25} & {1.30} & {1.35} & {1.40} \\ {1.40} & {1.50} & {1.60} & {1.70} & {1.80} \\ {0.10} & {0.25} & {0.35} & {0.40} & {0.50} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {0.5} \\ {0.5} \\ 0 \\ 0 \\ 0 \\ \end{array} } \right)$$
$$Z_{1} = 0.525; Z_{2} = 0.825; Z_{3} = 1.225; Z_{4} = 1.45; Z_{5} = 0.175;$$

For \({\text{A}}_{13} ;\)

$$\left( {\begin{array}{*{20}c} {Z_{1} } \\ {Z_{2} } \\ {Z_{3} } \\ {Z_{4} } \\ {Z_{5} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {0.50} & {0.55} & {0.60} & {0.65} & {0.60} \\ {0.90} & {0.75} & {0.65} & {0.60} & {0.50} \\ {1.20} & {1.25} & {1.30} & {1.35} & {1.40} \\ {1.40} & {1.50} & {1.60} & {1.70} & {1.80} \\ {0.10} & {0.25} & {0.35} & {0.40} & {0.50} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {0.5} \\ 0 \\ {0.5} \\ 0 \\ 0 \\ \end{array} } \right)$$
$$Z_{1} = 0.55; Z_{2} = 0.775;Z_{3} = 1.25; Z_{4} = 1.5; Z_{5} = 0.225;$$

For \({\text{A}}_{14} ;\)

$$\left( {\begin{array}{*{20}c} {Z_{1} } \\ {Z_{2} } \\ {Z_{3} } \\ {Z_{4} } \\ {Z_{5} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {0.50} & {0.55} & {0.60} & {0.65} & {0.60} \\ {0.90} & {0.75} & {0.65} & {0.60} & {0.50} \\ {1.20} & {1.25} & {1.30} & {1.35} & {1.40} \\ {1.40} & {1.50} & {1.60} & {1.70} & {1.80} \\ {0.10} & {0.25} & {0.35} & {0.40} & {0.50} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {0.5} \\ 0 \\ 0 \\ {0.5} \\ 0 \\ \end{array} } \right)$$
$$Z_{1} = 0.575; Z_{2} = 0.75;Z_{3} = 1.275; Z_{4} = 1.55;Z_{5} = 0.25;$$

For \({\text{A}}_{15} ;\)

$$\left( {\begin{array}{*{20}c} {Z_{1} } \\ {Z_{2} } \\ {Z_{3} } \\ {Z_{4} } \\ {Z_{5} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {0.50} & {0.55} & {0.60} & {0.65} & {0.60} \\ {0.90} & {0.75} & {0.65} & {0.60} & {0.50} \\ {1.20} & {1.25} & {1.30} & {1.35} & {1.40} \\ {1.40} & {1.50} & {1.60} & {1.70} & {1.80} \\ {0.10} & {0.25} & {0.35} & {0.40} & {0.50} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {0.5} \\ 0 \\ 0 \\ 0 \\ {0.5} \\ \end{array} } \right)$$
$$Z_{1} = 0.55; Z_{2} = 0.70;Z_{3} = 1.30; Z_{4} = 1.60;Z_{5} = 0.30$$

For \({\text{A}}_{23} ;\)

$$\left( {\begin{array}{*{20}c} {Z_{1} } \\ {Z_{2} } \\ {Z_{3} } \\ {Z_{4} } \\ {Z_{5} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {0.50} & {0.55} & {0.60} & {0.65} & {0.60} \\ {0.90} & {0.75} & {0.65} & {0.60} & {0.50} \\ {1.20} & {1.25} & {1.30} & {1.35} & {1.40} \\ {1.40} & {1.50} & {1.60} & {1.70} & {1.80} \\ {0.10} & {0.25} & {0.35} & {0.40} & {0.50} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 0 \\ {0.5} \\ {0.5} \\ 0 \\ 0 \\ \end{array} } \right)$$
$$Z_{1} = 0.575; Z_{2} = 0.70;Z_{3} = 1.275; Z_{4} = 1.55; Z_{5} = 0.30$$

For \({\text{A}}_{24} ;\)

$$\left( {\begin{array}{*{20}c} {Z_{1} } \\ {Z_{2} } \\ {Z_{3} } \\ {Z_{4} } \\ {Z_{5} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {0.50} & {0.55} & {0.60} & {0.65} & {0.60} \\ {0.90} & {0.75} & {0.65} & {0.60} & {0.50} \\ {1.20} & {1.25} & {1.30} & {1.35} & {1.40} \\ {1.40} & {1.50} & {1.60} & {1.70} & {1.80} \\ {0.10} & {0.25} & {0.35} & {0.40} & {0.50} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 0 \\ {0.5} \\ 0 \\ {0.5} \\ 0 \\ \end{array} } \right)$$
$$Z_{1} = 0.60; Z_{2} = 0.675;Z_{3} = 1.30; Z_{4} = 1.60;Z_{5} = 0.325$$

For \({\text{A}}_{25} ;\)

$$\left( {\begin{array}{*{20}c} {Z_{1} } \\ {Z_{2} } \\ {Z_{3} } \\ {Z_{4} } \\ {Z_{5} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {0.50} & {0.55} & {0.60} & {0.65} & {0.60} \\ {0.90} & {0.75} & {0.65} & {0.60} & {0.50} \\ {1.20} & {1.25} & {1.30} & {1.35} & {1.40} \\ {1.40} & {1.50} & {1.60} & {1.70} & {1.80} \\ {0.10} & {0.25} & {0.35} & {0.40} & {0.50} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 0 \\ {0.5} \\ 0 \\ 0 \\ {0.5} \\ \end{array} } \right)$$
$$Z_{1} = 0.575; Z_{2} = 0.625;Z_{3} = 1.325; Z_{4} = 1.65;Z_{5} = 0.375$$

For \({\text{A}}_{34} ;\)

$$\left( {\begin{array}{*{20}c} {Z_{1} } \\ {Z_{2} } \\ {Z_{3} } \\ {Z_{4} } \\ {Z_{5} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {0.50} & {0.55} & {0.60} & {0.65} & {0.60} \\ {0.90} & {0.75} & {0.65} & {0.60} & {0.50} \\ {1.20} & {1.25} & {1.30} & {1.35} & {1.40} \\ {1.40} & {1.50} & {1.60} & {1.70} & {1.80} \\ {0.10} & {0.25} & {0.35} & {0.40} & {0.50} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 0 \\ 0 \\ {0.5} \\ {0.5} \\ 0 \\ \end{array} } \right)$$
$$Z_{1} 0.625; Z_{2} = 0.625;Z_{3} = 1.325; Z_{4} = 1.65;Z_{5} = 0.375$$

For \({\text{A}}_{35} ;\)

$$\left( {\begin{array}{*{20}c} {Z_{1} } \\ {Z_{2} } \\ {Z_{3} } \\ {Z_{4} } \\ {Z_{5} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {0.50} & {0.55} & {0.60} & {0.65} & {0.60} \\ {0.90} & {0.75} & {0.65} & {0.60} & {0.50} \\ {1.20} & {1.25} & {1.30} & {1.35} & {1.40} \\ {1.40} & {1.50} & {1.60} & {1.70} & {1.80} \\ {0.10} & {0.25} & {0.35} & {0.40} & {0.50} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 0 \\ 0 \\ {0.5} \\ 0 \\ {0.5} \\ \end{array} } \right)$$
$$Z_{1} = 0.60; Z_{2} = 0.575;Z_{3} = 1.35; Z_{4} = 1.70;Z_{5} = 0.425$$

For \({\text{A}}_{45} ;\)

$$\left( {\begin{array}{*{20}c} {Z_{1} } \\ {Z_{2} } \\ {Z_{3} } \\ {Z_{4} } \\ {Z_{5} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {0.50} & {0.55} & {0.60} & {0.65} & {0.60} \\ {0.90} & {0.75} & {0.65} & {0.60} & {0.50} \\ {1.20} & {1.25} & {1.30} & {1.35} & {1.40} \\ {1.40} & {1.50} & {1.60} & {1.70} & {1.80} \\ {0.10} & {0.25} & {0.35} & {0.40} & {0.50} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ {0.5} \\ {0.5} \\ \end{array} } \right)$$
$$Z_{1} = 0.625; Z_{2} = 0.55;Z_{3} = 1.375; Z_{4} = 1.75;Z_{5} = 0.45$$

The values of real components (Z1, Z2, Z3, Z4 and Z5) calculated are summarized in Table 1. While for the control points are shown in Table 2.

Table 1 Mixture formulation matrix table
Full size table
Table 2 Mixture proportion of control points showing actual and pseudo components
Full size table

1.3 Mixture proportion of control points showing actual and pseudo components

To test the adequacy of the generated model, the control points’ mixture formulation is computed with the response used to validate the optimization, the computation for the fifteen points are as follows;

For control point A1

$$\left( {\begin{array}{*{20}c} {Z_{1} } \\ {Z_{2} } \\ {Z_{3} } \\ {Z_{4} } \\ {Z_{5} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {0.50} & {0.55} & {0.60} & {0.65} & {0.60} \\ {0.90} & {0.75} & {0.65} & {0.60} & {0.50} \\ {1.20} & {1.25} & {1.30} & {1.35} & {1.40} \\ {1.40} & {1.50} & {1.60} & {1.70} & {1.80} \\ {0.10} & {0.25} & {0.35} & {0.40} & {0.50} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {0.3} \\ {0.3} \\ {0.3} \\ {0.1} \\ 0 \\ \end{array} } \right)$$
$$Z_{1} = 0.56; Z_{2} = 0.75;Z_{3} = 1.26;Z_{4} = 1.22;Z_{5} = 0.25$$

For control point A2

$$\left( {\begin{array}{*{20}c} {Z_{1} } \\ {Z_{2} } \\ {Z_{3} } \\ {Z_{4} } \\ {Z_{5} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {0.50} & {0.55} & {0.60} & {0.65} & {0.60} \\ {0.90} & {0.75} & {0.65} & {0.60} & {0.50} \\ {1.20} & {1.25} & {1.30} & {1.35} & {1.40} \\ {1.40} & {1.50} & {1.60} & {1.70} & {1.80} \\ {0.10} & {0.25} & {0.35} & {0.40} & {0.50} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {0.3} \\ {0.3} \\ {0.3} \\ 0 \\ {0.1} \\ \end{array} } \right)$$
$$Z_{1} = 0.555; Z_{2} = 0.74;Z_{3} = 1.265;Z_{4} = 1.23;Z_{5} = 0.26$$

For control point A3

$$\left( {\begin{array}{*{20}c} {Z_{1} } \\ {Z_{2} } \\ {Z_{3} } \\ {Z_{4} } \\ {Z_{5} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {0.50} & {0.55} & {0.60} & {0.65} & {0.60} \\ {0.90} & {0.75} & {0.65} & {0.60} & {0.50} \\ {1.20} & {1.25} & {1.30} & {1.35} & {1.40} \\ {1.40} & {1.50} & {1.60} & {1.70} & {1.80} \\ {0.10} & {0.25} & {0.35} & {0.40} & {0.50} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {0.3} \\ {0.3} \\ 0 \\ {0.3} \\ {0.1} \\ \end{array} } \right)$$
$$Z_{1} = 0.57; Z_{2} = 0.725;Z_{3} = 1.28;Z_{4} = 1.26;Z_{5} = 0.275$$

For control point A4

$$\left( {\begin{array}{*{20}c} {Z_{1} } \\ {Z_{2} } \\ {Z_{3} } \\ {Z_{4} } \\ {Z_{5} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {0.50} & {0.55} & {0.60} & {0.65} & {0.60} \\ {0.90} & {0.75} & {0.65} & {0.60} & {0.50} \\ {1.20} & {1.25} & {1.30} & {1.35} & {1.40} \\ {1.40} & {1.50} & {1.60} & {1.70} & {1.80} \\ {0.10} & {0.25} & {0.35} & {0.40} & {0.50} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {0.3} \\ 0 \\ {0.3} \\ {0.3} \\ {0.1} \\ \end{array} } \right)$$
$$Z_{1} = 0.585; Z_{2} = 0.695;Z_{3} = 1.295;Z_{4} = 1.29;Z_{5} = 0.305$$

For control point A5

$$\left( {\begin{array}{*{20}c} {Z_{1} } \\ {Z_{2} } \\ {Z_{3} } \\ {Z_{4} } \\ {Z_{5} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {0.50} & {0.55} & {0.60} & {0.65} & {0.60} \\ {0.90} & {0.75} & {0.65} & {0.60} & {0.50} \\ {1.20} & {1.25} & {1.30} & {1.35} & {1.40} \\ {1.40} & {1.50} & {1.60} & {1.70} & {1.80} \\ {0.10} & {0.25} & {0.35} & {0.40} & {0.50} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 0 \\ {0.3} \\ {0.3} \\ {0.3} \\ {0.1} \\ \end{array} } \right)$$
$$Z_{1} = 0.600; Z_{2} = 0.650;Z_{3} = 1.310;Z_{4} = 1.620;Z_{5} = 0.350$$

For control point A12

$$\left( {\begin{array}{*{20}c} {Z_{1} } \\ {Z_{2} } \\ {Z_{3} } \\ {Z_{4} } \\ {Z_{5} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {0.50} & {0.55} & {0.60} & {0.65} & {0.60} \\ {0.90} & {0.75} & {0.65} & {0.60} & {0.50} \\ {1.20} & {1.25} & {1.30} & {1.35} & {1.40} \\ {1.40} & {1.50} & {1.60} & {1.70} & {1.80} \\ {0.10} & {0.25} & {0.35} & {0.40} & {0.50} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {0.25} \\ {0.25} \\ {0.25} \\ {0.25} \\ 0 \\ \end{array} } \right)$$
$$Z_{1} = 0.575; Z_{2} = 0.725;Z_{3} = 1.275;Z_{4} = 1.300;Z_{5} = 0.275$$

For control point A13

$$\left( {\begin{array}{*{20}c} {Z_{1} } \\ {Z_{2} } \\ {Z_{3} } \\ {Z_{4} } \\ {Z_{5} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {0.50} & {0.55} & {0.60} & {0.65} & {0.60} \\ {0.90} & {0.75} & {0.65} & {0.60} & {0.50} \\ {1.20} & {1.25} & {1.30} & {1.35} & {1.40} \\ {1.40} & {1.50} & {1.60} & {1.70} & {1.80} \\ {0.10} & {0.25} & {0.35} & {0.40} & {0.50} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {0.25} \\ {0.25} \\ {0.25} \\ 0 \\ {0.25} \\ \end{array} } \right)$$
$$Z_{1} = 0.5625; Z_{2} = 0.700;Z_{3} = 1.2875;Z_{4} = 1.325;Z_{5} = 0.300$$

For control point A14

$$\left( {\begin{array}{*{20}c} {Z_{1} } \\ {Z_{2} } \\ {Z_{3} } \\ {Z_{4} } \\ {Z_{5} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {0.50} & {0.55} & {0.60} & {0.65} & {0.60} \\ {0.90} & {0.75} & {0.65} & {0.60} & {0.50} \\ {1.20} & {1.25} & {1.30} & {1.35} & {1.40} \\ {1.40} & {1.50} & {1.60} & {1.70} & {1.80} \\ {0.10} & {0.25} & {0.35} & {0.40} & {0.50} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {0.25} \\ {0.25} \\ 0 \\ {0.25} \\ {0.25} \\ \end{array} } \right)$$
$$Z_{1} = 0.575; Z_{2} = 0.6875;Z_{3} = 1.300;Z_{4} = 1.350;Z_{5} = 0.3125$$

For control point A15

$$\left( {\begin{array}{*{20}c} {Z_{1} } \\ {Z_{2} } \\ {Z_{3} } \\ {Z_{4} } \\ {Z_{5} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {0.50} & {0.55} & {0.60} & {0.65} & {0.60} \\ {0.90} & {0.75} & {0.65} & {0.60} & {0.50} \\ {1.20} & {1.25} & {1.30} & {1.35} & {1.40} \\ {1.40} & {1.50} & {1.60} & {1.70} & {1.80} \\ {0.10} & {0.25} & {0.35} & {0.40} & {0.50} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {0.25} \\ 0 \\ {0.25} \\ {0.25} \\ {0.25} \\ \end{array} } \right)$$
$$Z_{1} = 0.5875; Z_{2} = 0.6625;Z_{3} = 1.3125;Z_{4} = 1.375;Z_{5} = 0.3375$$

For control point A23

$$\left( {\begin{array}{*{20}c} {Z_{1} } \\ {Z_{2} } \\ {Z_{3} } \\ {Z_{4} } \\ {Z_{5} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {0.50} & {0.55} & {0.60} & {0.65} & {0.60} \\ {0.90} & {0.75} & {0.65} & {0.60} & {0.50} \\ {1.20} & {1.25} & {1.30} & {1.35} & {1.40} \\ {1.40} & {1.50} & {1.60} & {1.70} & {1.80} \\ {0.10} & {0.25} & {0.35} & {0.40} & {0.50} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 0 \\ {0.25} \\ {0.25} \\ {0.25} \\ {0.25} \\ \end{array} } \right)$$
$$Z_{1} = 0.600; Z_{2} = 0.625;Z_{3} = 1.325;Z_{4} = 1.650;Z_{5} = 0.375$$

For control point A24

$$\left( {\begin{array}{*{20}c} {Z_{1} } \\ {Z_{2} } \\ {Z_{3} } \\ {Z_{4} } \\ {Z_{5} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {0.50} & {0.55} & {0.60} & {0.65} & {0.60} \\ {0.90} & {0.75} & {0.65} & {0.60} & {0.50} \\ {1.20} & {1.25} & {1.30} & {1.35} & {1.40} \\ {1.40} & {1.50} & {1.60} & {1.70} & {1.80} \\ {0.10} & {0.25} & {0.35} & {0.40} & {0.50} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {0.15} \\ {0.15} \\ {0.15} \\ {0.15} \\ {0.40} \\ \end{array} } \right)$$
$${\text{Z}}_{1} = 0.600;{ }Z_{2} = 0.635;Z_{3} = 1.325;Z_{4} = 1.500;Z_{5} = 0.365$$

For control point A25

$$\left( {\begin{array}{*{20}c} {Z_{1} } \\ {Z_{2} } \\ {Z_{3} } \\ {Z_{4} } \\ {Z_{5} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {0.50} & {0.55} & {0.60} & {0.65} & {0.60} \\ {0.90} & {0.75} & {0.65} & {0.60} & {0.50} \\ {1.20} & {1.25} & {1.30} & {1.35} & {1.40} \\ {1.40} & {1.50} & {1.60} & {1.70} & {1.80} \\ {0.10} & {0.25} & {0.35} & {0.40} & {0.50} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {0.15} \\ {0.15} \\ {0.15} \\ {0.40} \\ {0.15} \\ \end{array} } \right)$$
$${\text{Z}}_{1} = 0.5975;Z_{2} = 0.660;Z_{3} = 1.3125;Z_{4} = 1.475;Z_{5} = 0.340$$

For control point A34

$$\left( {\begin{array}{*{20}c} {Z_{1} } \\ {Z_{2} } \\ {Z_{3} } \\ {Z_{4} } \\ {Z_{5} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {0.50} & {0.55} & {0.60} & {0.65} & {0.60} \\ {0.90} & {0.75} & {0.65} & {0.60} & {0.50} \\ {1.20} & {1.25} & {1.30} & {1.35} & {1.40} \\ {1.40} & {1.50} & {1.60} & {1.70} & {1.80} \\ {0.10} & {0.25} & {0.35} & {0.40} & {0.50} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {0.15} \\ {0.15} \\ {0.40} \\ {0.15} \\ {0.15} \\ \end{array} } \right)$$
$${\text{Z}}_{1} = 0.585;{ }Z_{2} = 0.6725;Z_{3} = 1.300;Z_{4} = 1.45;Z_{5} = 0.3275$$

For control point A35

$$\left( {\begin{array}{*{20}c} {Z_{1} } \\ {Z_{2} } \\ {Z_{3} } \\ {Z_{4} } \\ {Z_{5} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {0.50} & {0.55} & {0.60} & {0.65} & {0.60} \\ {0.90} & {0.75} & {0.65} & {0.60} & {0.50} \\ {1.20} & {1.25} & {1.30} & {1.35} & {1.40} \\ {1.40} & {1.50} & {1.60} & {1.70} & {1.80} \\ {0.10} & {0.25} & {0.35} & {0.40} & {0.50} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {0.15} \\ {0.40} \\ {0.15} \\ {0.15} \\ {0.15} \\ \end{array} } \right)$$
$${\text{Z}}_{1} = 0.5725;Z_{2} = 0.6975;Z_{3} = 1.2875;Z_{4} = 1.425;Z_{5} = 0.3025$$

For control point A45

$$\left( {\begin{array}{*{20}c} {Z_{1} } \\ {Z_{2} } \\ {Z_{3} } \\ {Z_{4} } \\ {Z_{5} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {0.50} & {0.55} & {0.60} & {0.65} & {0.60} \\ {0.90} & {0.75} & {0.65} & {0.60} & {0.50} \\ {1.20} & {1.25} & {1.30} & {1.35} & {1.40} \\ {1.40} & {1.50} & {1.60} & {1.70} & {1.80} \\ {0.10} & {0.25} & {0.35} & {0.40} & {0.50} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {0.40} \\ {0.15} \\ {0.15} \\ {0.15} \\ {0.15} \\ \end{array} } \right)$$
$${\text{Z}}_{1} = 0.560;{ }Z_{2} = 0.735;Z_{3} = 1.275;Z_{4} = 1.150;Z_{5} = 0.265$$

2 Materials and methods

2.1 Materials

The constituent ingredient materials used in this experimental investigation include cement, rice husk ash, fine and coarse aggregate and water. The Unicem brand of Portland Limestone Cement of grade 32.5 used in this study was purchased in an open market and it matches with the requirements of CEM II class of cements as defined in NIS 444-1 [18] composition, specifications and conformity criteria for common cements. Rice husk is an agricultural waste obtained during rice processing and production. The Rice husk ash (RHA) was obtained from a rice processing mill in Obubra Local Government Area, Cross River State and physical observation showed that RHA is greyish in colour after burning. The fine aggregates used for this study is river sand, collected from a river bed in Mkpat Enin, Akwa Ibom State, Nigeria and was prepared to BS EN 12620 [19]. The Coarse aggregate used for the experiment is crushed granite of maximum size 20 mm and conforms to BS EN 12620 [19]. Also, water which is an important constituent was used throughout the experimental investigation. The source of water for the experiment is within Akwa Ibom State University campus. It satisfies ASTM C1602-12 [20] requirement of water for use in concrete mixtures.

2.2 Methods

The methods used for this research work involves firstly the preparation of materials, characterization of the materials, gradation of the aggregates used, production of concrete samples according to the formulated mixture proportions, finally testing and development of the Scheffe’s regression model. The flow chart showing methodology of Scheffe’s model development which was adapted for this research study is shown in Fig. 2.

Fig. 2
figure 2

Methodology of Scheffe’s model development flow chart

Full size image

2.2.1 Oxide composition

The dominant elemental oxide composition of rice husk ash (RHA) was obtained at Defense Industry Co-operation of Nigeria (DICON), Kaduna, Nigeria, using the method of X-Ray Fluorescence.

2.2.2 Compressive strength test

The compressive strength test is used to ascertain the behaviour of materials under a compression load. Generally, compressive strength is commonly considered as the most important property of concrete. Three replicate concrete samples were made for the thirty mix ratios each in 150 mm × 150 mm × 150 mm moulds. After mixing and casting of the concrete, the concrete specimens are demoulded and cured for 28 days in a curing tank and then tested to ascertain its response with respect to compressive strength in accordance with BS EN 12390 [21]. The compressive strength of concrete was determined using the formula:

$${\text{F}} = \frac{{\text{P}}}{{\text{A}}}$$
(11)

where P is the failure load; A is the cross sectional area of the cube.

3 Results and discussion

3.1 Materials characterization

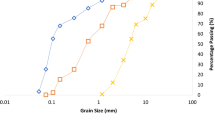
The particle size distribution for fine and coarse aggregates is shown in Figs. 3 and 4, respectively. The fine and coarse aggregates were sieved with the largest particles at 4.75 mm and 20 mm respectively in the BSI sieve. For the fine aggregate, the particle size distribution is shown in Fig. 3 and it reveals that the sand falls within zone 2 according to the grading limits for fine aggregates BS 882 [22], which lies within the acceptable range suitable for construction purposes. The sand satisfies the requirement of lower and upper limits of the percentage by mass passing as specified by BS 882 [22]. From the grading curve, it could be observed that the Coefficient of uniformity (Cu) and Coefficient of curvature (Cc) for the fine aggregates are 1.87 and 1.14 respectively. Thus, the sand can be said to be classified as uniformly graded since the value of Cu is less than 2 as stipulated in ASTM D 422-63 [23] whereas the coefficient of curvature (Cc) for coarse aggregate is 1.05.

Fig. 3
figure 3

Particle size distribution for fine aggregate

Full size image
Fig. 4
figure 4

Particle size distribution for coarse aggregate

Full size image

The chemical composition of RHA portrays that it is a highly reactive pozzolana due to a combined Al2O3, Fe2O3 and SiO2 content of 78.68%, which is higher than the minimum value of 70% as stipulated in ASTM C 618 [24]. The specific gravity of RHA was found to be 2.10 which falls within the range of 1.9 and 2.4 specified for pulverized fuel ash (PFA) as reported by Neville [25] while the specific gravity of cement was 3.15. The chemical composition of rice husk ash and Portland limestone cement used is presented in Table 3.

Table 3 Chemical properties of materials
Full size table

3.2 Compressive strength

The average 28 day compressive strength test result of laboratory response and average 28 day compressive strength test result showing the maximum and minimum obtainable response within the factor space is presented in Table 4.

Table 4 The 28 days compressive strength laboratory response
Full size table

3.3 Scheffe’s coefficients

The Scheffe’s coefficients of a second degree polynomial is determined from Eq. (10) which are as follows:

$${\upbeta }_{1} = 24,{{ \upbeta }}_{2} = 27.35,{{ \upbeta }}_{3} = 33.45,{{ \upbeta }}_{4} = 21,{{ \upbeta }}_{5} = 16.95,{{ \upbeta }}_{12} = 23.30,{{ \upbeta }}_{13} = 1.1, {\upbeta }_{14} = 21.40,{{ \upbeta }}_{15} = 22.10,{\upbeta }_{23} = - 15.40,{{ \upbeta }}_{24} = 3.30,{\upbeta }_{25} = 5.40,{\upbeta }_{34} = - 16.90, {\upbeta }_{35} = 23.80,{\upbeta }_{45} = - 3.90$$

Therefore, substituting the coefficients’ values into Eq. (9) yields:

$${\text{Y}}_{{{\text{Comp}}}} = 24{\text{X}}_{1} + 27.35{\text{X}}_{2} + { }33.45{\text{X}}_{3} + 21{\text{X}}_{4} + { }16.95{\text{X}}_{5} + 23.3{\text{X}}_{1} {\text{ X}}_{2} + 1.1{\text{X}}_{1} {\text{X}}_{3} + { }21.4{\text{X}}_{1} {\text{X}}_{4} + { }22.1{\text{X}}_{1} {\text{X}}_{5} - { }15.4{\text{X}}_{2} {\text{X}}_{3} + { }3.3{\text{X}}_{2} {\text{X}}_{4} + { }5.4{\text{X}}_{2} {\text{X}}_{5} - { }16.9{\text{X}}_{3} {\text{X}}_{4} - 23.8{\text{X}}_{3} {\text{X}}_{5} - { }3.9{\text{X}}_{4} {\text{X}}_{5}$$
(12)

Equation (12) is the modelled mathematical relationship to aid in optimization of compressive strength of rice husk ash concrete.

3.4 Validation and test of adequacy of the model

To ascertain whether the formulated model in Eq. (12) is acceptable to be used in predicting compressive strength, it is essential to carry out statistical test. The test for adequacy of the model was carried out with the aid of student’s t test and analysis of variance. Fifteen extra points were used to test the model’s validity and adequacy of the model was tested by comparing the experimental results of the control points with the predicted results. In this test, the two hypotheses tested are that:

There is no significant difference between the obtained laboratory results of the compressive strength and the model predicted values at 0.05 critical value \(\left( \alpha \right)\), this is the null hypothesis.

There is a significant difference between the obtained laboratory results of the compressive strength and the model predicted values at 0.05 critical value \(\left( \alpha \right)\), this is the alternate hypothesis.

3.4.1 Student’s t test results

A two-tailed student t test at 0.05 critical value \(\left( \alpha \right)\) was used to compare the two groups the criteria for decision is if t stat > t Critical two-tail, we reject the null hypothesis. Table 5 presents the experimental result and model result of compressive strength for the control points. For the t test, the t stat = -0.248389831 and t critical two-tail = 2.144786688, so t critical > t stat. Therefore, we accept the null hypothesis. The results is presented in Table 6.

Table 5 The experimental and model results for the control points
Full size table
Table 6 T-Test: paired two sample for means
Full size table

3.4.2 Analysis of Variance

If F > F crit, we reject the null hypothesis of the analysis of variance. Table 7 presents the result of the analysis, F = 0.006942 and F crit = 4.19597 so F crit > F. Therefore, we do not reject null hypothesis. However, this infers that there was no significant difference between the experiment result and the model result. Henceforth, the model is satisfactory for use in predicting the compressive strength of rice husk ash blended cement concrete.

Table 7 Anova single factor
Full size table

3.5 Discussion of results

Generally, Scheffe’s simplex method was applied in this study and the results of 28 days compressive strength were obtained. The results of the compressive strength obtained from both the laboratory response and model response are displayed in Tables 4 and 5. Based on the formulated model, the peak value of compressive strength of 33.45 N/mm2 was achieved with a corresponding mix ratio of 0.60: 0.65: 1.30: 1.60: 0.35 for fraction of water, cement, fine aggregate, coarse aggregate and rice husk ash respectively. It is interesting to note that the addition of about 7.78% by weight of rice husk ash to the concrete mix with a water cement ratio of 0.60 resulted to the peak value of compressive strength. The lowest compressive strength response was found to be 16.95 N/mm2 and this was as a result of adding about 10.42% by weight of rice husk ash to the concrete mix with a water cement ratio of 0.60. The optimization results achieved in this study indicates that both the minimum and maximum compressive strength of 16.95 and 33.45 N/mm2 were within the standard compressive strength of Portland Limestone cement grade 32.5 at 7 and 28 days respectively, as recommended in [26]. However, the peak value of 28 days compressive strength was above the minimum requirement of 20 and 25 N/mm2 cube strength of concrete for structural use NCP 1 [27] and for reinforced concrete according to BS 8110: Part 1 [28]. This result portrays that RHA been a good SCM could still be used as a construction material in concrete structures in a bid to improve environmental protection, eradicate waste management problem and sustainability.

4 Conclusion

In this study, Scheffe’s second degree polynomial was applied in formulating model for the optimization of compressive strength of rice husk ash blended cement concrete. The result revealed that the response predicted by the formulated model is in good agreement with the corresponding experimentally observed results. The maximum value of compressive strength of 33.45 N/mm2 was achieved with a corresponding mix ratio of 0.60: 0.65: 1.30: 1.60: 0.35 for fraction of water, cement, fine aggregate, coarse aggregate and rice husk ash respectively. Also, the minimum compressive strength response was found to be 16.95 N/mm2 with a corresponding mix ratio of 0.60: 0.50: 1.40: 1.8: 0.5. Based on the test of adequacy, student t test and the analysis of variance (ANOVA) test at 95% confidence level were applied to check the adequacy of the models and from the results, the p-value of 0.93 for the ANOVA while P (T ≤ t) two tail of 0.807 which indicates a very strong correlation between the experimental and model control results.