1 Introduction

A time series is loosely defined as a set containing measures of a random variable of interest, ordered in time. Thus, an electric energy load curve is a time series; consequently, the time series prediction and analysis techniques can be applied to estimate the future behavior of electric power demand [1].

The capacity to forecast electrical power demand time series is associated with the efficiency and efficacy of electric energy planning, which improves the financial results of the players in the industry [2, 3]. Once the predictors are robust and accurate, the results are used as input in tasks such as expansion planning, economical operation, security analysis, and control. So, if the demand is not adequately forecast, it can lead to financial losses for the utilities as well as for the users. The utilities lose when buying electrical energy with high costs, energy losses, and possible high financial penalties, depending on market design. The users are penalized according to their consumer class, with power interruptions and low-quality indexes.

Introducing information technologies in distribution networks, a process known as Smart Grids, will facilitate data acquisition at several aggregation levels. Electrical demand data are currently available for long time periods, with high resolution and in scenarios previously ignored, for example, individual consumers or small groups [4]. This data can be called disaggregated, as it is collected in more detailed levels than the usual; in a load curve context, it means to approach individual consumption levels in high time resolution.

There are some works on the literature dealing with these kinds of data, and they can be divided in two groups, such as residential [5,6,7,8,9,10,11] and nonresidential [12,13,14,15,16,17,18,19].

Thus, the electrical energy demand time series become larger, more disaggregated, and more detailed. These characteristics bring difficulties to the forecasting process, specially due the low aggregation level. It consists of data with high variability, resulting from the fact that it depends on the number of persons consuming simultaneously, the number of electric equipment turned on, etc. In contrast, in aggregated levels the fluctuations and noises of the individual consumers may cancel each other out while taking the sum [3].

The literature presents several prediction methods, which can, roughly, be divided in two groups: statistical and computational intelligence. The statistical includes, among others, the ARIMA family (Autoregressive integrated moving average), such as ARIMA, Seasonal ARIMA, and ARIMAX; another group contains ANNs (artificial neural networks), fuzzy logic, among others [20]. Each method presents its own advantages and disadvantages, depending on the characteristics of the time series, data quantity, and others.

For predictions in disaggregated levels, as the consumption can fluctuate heavily even in consecutive hours or consecutive days from any regular pattern [3], the principal characteristics to consider are the resolution and the data quantity, the randomness of the time series, atypical days, and noise levels.

For noise removal, this paper uses singular spectrum analysis (SSA), which is an algorithm with advantages over others used for the same task. SSA requires only two parameters to be chosen: window length and the eigenvectors used for the reconstructing. Analytical methods are not available to determine the former; nevertheless, the results are not overly sensitive to small variations of it [21]. For the latter, automatic selection strategies can be adopted based on hierarchical clustering. Unlike traditional methods, this technique works adequately for stationary signals as well as non-stationary signals. It is easily implementable and has low computational costs [22].

Noise removal is not common in load forecasting literature because most works are based on low-resolution data from large aggregated areas, where the problem is not common. However, some works show the advantages of preprocessing the data sets. For example, Ref. [23] showed accuracy in applying a moving average filter with delay corrector to the data to predict substation load demand with a general regression neural network (GRNN). In Ref. [24], an SSA filter is used to remove noise in the time series to be predicted in a feedforward neural network, thus improving the results as compared to prediction with rough data. The authors in [25] attained good results by applying SSA to further use autoregressive models for short-term load forecasting. Ref. [26] performed electrical load forecasting using an MLP (multi-layer perceptron) neural network optimized by metaheuristics and reducing noise with SSA. The authors in [27] presented good results using support vector regression optimized by the Cuckoo Search algorithm, as well as reducing the noise with SSA.

In the other hand, Fuzzy ARTMAP ANN has been shown to be a good option in terms of load forecasting. For example, references [28,29,30,31,32] have presented good results in comparison with other forecasting methods.

Therefore, it seems to be a logical approach to combine these two techniques aiming better forecast results. However, as there is no record in the literature of applying SSA together with Fuzzy ARTMAP ANN for load forecasting, this is an original contribution of this paper. In addition, in most of the literature, the load curves present less resolution and higher level of aggregation of electrical loads than the ones studied in this work (large geographical regions). The work herein is significantly different from previous works, in that disaggregated data are used along with a neural network based on adaptive resonance theory.

The data used in this work presents days with atypical load curves. It happens due to weekends, holydays and others. In disaggregated levels, they may cause a huge variation from the usual pattern [7]. Traditional predictors cannot incorporate the analyst’s previous knowledge to the model without adaptations. According to [33], the loads of these atypical days are different from other days and cannot be predicted, thus damaging the prediction of typical days.

Ref. [33] showed that the treatment of atypical days is not common in the literature, and sometimes they are substituted on the original series by forecasting within the sample for that day or a pre-determined day, manipulating the data to consider it as a typical day [34, 35]. This approach, however, does not consider the information contained that possibly could aid modeling the behavior of the following days. Another approach consists of separating atypical days from weekends and labor days by introducing a dummy variable, according to [33, 36, 37].

However, the causes of such behavior are not always known; therefore, it is important that the predictor is able to mitigate this situation.

This work compares three forecasting methods: a statistical model, SARIMA (seasonal autoregressive integrated moving average), because the data is seasonal; and two others from computational intelligence, i.e., MLP and Fuzzy ARTMAP, applied to short-term load forecasting (1, 3, and 7 days), with and without noise removal. The data originates from an intelligent microgrid (smart micro grid) in Brazil. Identifying weekends and atypical days is a task that the Fuzzy ARTMAP performs very well and is superior compared to the other methodologies tested, which cannot identify a normal day from an atypical day or a weekend. The noise removal with SSA for further modeling by the Fuzzy ARTMAP improves the forecasted results.

2 Scenario of study

This work uses real data from a smart microgrid in Foz do Iguassu, Brazil, and the load curve is composed of commercial sites, startups, research centers, laboratories, offices, and services.

Two scenarios of the same smart microgrid were studied, one composed by 46 daily measurements with interval of 30 min between them, and another, with 96 daily data, with an interval of 15 min. The patterns sets correspond to January, February, and March of 2017 (from January 1 to March 31). The data is available upon request from the authors.

The labor days are different and present variations; otherwise, the weekend demands are lower than that of labor days. In addition, atypical days exist in the time series used. Figure 1 presents the week prior to a national holiday in Brazil (Carnival), the week of the holiday, and the week following to the holiday (February 19 to March 11).

Fig. 1
figure 1

Load curves prior to, during, and following Carnival

Full size image

3 Fuzzy ARTMAP artificial neural network

The first mathematical neuron based on a biological neuron was presented in [38], leading to the first artificial neural network. This work forms the basis of further computational implementations [39], based on the ability of live organisms to assimilate knowledge when facing new situations.

ANNs can present answers even with data different from the training sets, which is the capacity to generalize. Different ANN architectures have been proposed to improve beyond the limits of previous ones or to perform new tasks [40].

Adaptive resonance theory (ART) neural networks are examples of an ANN development. ART theory solves the plasticity/stability problem, where the stability assures that every element has a category created, being plasticity the capacity to assume new patterns without losing the previously acquired knowledge.

Fuzzy ARTMAP ANN pertains to the supervised training paradigm, with the calculus based on fuzzy logic. The architecture is composed of two Fuzzy ART modules (\({\text{ART}}_{a}\) and \({\text{ART}}_{b}\)), where the \({\text{ART}}_{a}\) module processes the input vector and the \({\text{ART}}_{b}\) module processes the desired output vector.

The associative memory module Inter-ART receives the inputs of the \({\text{ART}}_{a}\) module (referred to as the associative connection J → K, where \(J\) and \(K\) are the active categories in modules \({\text{ART}}_{a}\) and \({\text{ART}}_{b}\), respectively. This module contains an auto-regulator mechanism called Match Tracking, which matches the categories of \({\text{ART}}_{a}\) with \({\text{ART}}_{b}\) [17]. The Fuzzy ARTMAP architecture is shown in Fig. 2.

Fig. 2
figure 2

Fuzzy ARTMAP ANN [14]

Full size image

First, none of the categories are active; therefore, the weight matrix (\(w\)) is 1. As the pairs in \({\text{ART}}_{a}\) and \({\text{ART}}_{b}\) are confirmed (according to Match-Tracking), the categories become active.

Below, the steps of Fuzzy ARTMAP ANN are shown:

  • Initial Module:

  • Reading the input (A) and output (B) patterns for training:

    $$A = \left[ {a_{1} ,a_{2} , \ldots ,a_{n} } \right]\,{\text{and}}\,B = \left[ {b_{1} ,b_{2} , \ldots ,b_{n} } \right];$$

  • Normalization of input (A) and output (B) vectors:

    $$\bar{a} = \frac{a}{\left| a \right|}\,{\text{and}}\,\bar{b} = \frac{b}{\left| b \right|},\,{\text{where}}\,\left| a \right| = \mathop \sum \limits_{i} \left| {a_{i} } \right|$$
    (1)

  • Input (A) and output (B) complement:

    $$\bar{a}_{i}^{c} = 1 - a_{i} \,{\text{and}}\,\bar{b}_{i}^{c} = 1 - b_{i} ;$$
    (2)

  • Input (A) and output (B) vectors normalized and complemented:

    $$I^{e} = \left[ {a\bar{a}} \right]\,{\text{and}}\,I^{s} = \left[ {b\bar{b}} \right];$$
    (3)

  • Initialization of weight matrices (value 1):

    $$w_{j}^{a} = 1;\,w_{k}^{b} = 1;\,w_{j}^{ab} = 1;\,{\text{showing}}\,{\text{that}}\,{\text{there}}\,{\text{is}}\,{\text{no}}\,{\text{active}}\,{\text{category}} .$$

  • Reading the parameters:

    $$\alpha ,\beta ,\rho_{a} ,\rho_{b} ,\rho_{ab} \,{\text{and}}\,\varepsilon ;$$

  • Fuzzy ARTb Module:

  • Calculus of function \(T_{k}^{b}\):

    $$T_{k}^{b} \left( {I^{s} } \right) = \frac{{\left| {I^{s} \wedge w_{k}^{b} } \right|}}{{\alpha + w_{k}^{b} }};$$
    (4)

  • Choose the category (\(K\)) for module Fuzzy ARTb:

    $$T_{k}^{b} = \hbox{max} \left\{ {T_{k}^{b} :k = 1, \ldots ,N_{b} } \right\} ;$$
    (5)

  • Verify if the vigilance criterion for Fuzzy ARTb is attended:

    $$\left| {x^{b} } \right| = \frac{{\left| {I^{s} \wedge w_{k}^{b} } \right|}}{{\left| {I^{s} } \right|}} \ge \rho_{b} ;$$
    (6)

  • If not: Reset: \(T_{k}^{b} = 0\);

  • If yes:

    Resonance, adaptation of Fuzzy ARTb weights

    $$w_{K}^{\text{new}} = \beta \left( {I^{s} \wedge w_{K}^{\text{old}} } \right) + \left( {1 - \beta } \right)w_{K}^{\text{old}} ;$$
    (7)

    and

    Calculus of the activity vector in \(F_{2}\):

    $$y_{k}^{b} = \left[ {y_{1}^{b} ,y_{2}^{b} , \ldots ,y_{N}^{b} } \right],\,{\text{where}}:y_{k}^{b} = \left\{ {\begin{array}{*{20}c} {1,} & {{\text{if}}\,\,k = K} \\ {0,} & {{\text{if}}\,\,k \ne K} \\ \end{array} } \right.$$
    (8)

  • Go to the Match Tracking module;

  • Fuzzy ART a Module:

  • Calculus of function \(T_{j}^{a}\):

    $$T_{j}^{a} \left( {I^{e} } \right) = \frac{{\left| {I^{e} \wedge w_{j}^{a} } \right|}}{{\alpha + w_{j}^{a} }}$$
    (9)

  • Choose the category (\(J\)) Fuzzy ARTa Module:

    $$T_{j}^{a} = \hbox{max} \left\{ {T_{j}^{a} :j = 1, \ldots ,N_{a} } \right\}$$
    (10)

  • Verify the vigilance criterion of Fuzzy ARTa Module:

    $$\left| {x^{a} } \right| = \frac{{\left| {I^{e} \wedge w_{j}^{a} } \right|}}{{\left| {I^{e} } \right|}} \ge \rho_{a}$$
    (11)

  • If yes: Calculus of activity vector in \(F_{2}\): \(y_{j}^{a} = \left[ {y_{1}^{a} ,y_{2}^{a} , \ldots ,y_{N}^{a} } \right]\), where:

    $$y_{j}^{a} = \left\{ {\begin{array}{*{20}c} {1,} & {{\text{if}}\,\,j = J} \\ {0,} & {{\text{if}}\,\,j \ne J} \\ \end{array} } \right.$$
    (12)

  • Go to the Match Tracking module;

  • Match Tracking module:

  • Verify if the vigilance criterion of Inter-ART module is attended:

    $$\left| {x^{ab} } \right| = \frac{{\left| {y^{b} \wedge w_{j}^{ab} } \right|}}{{\left| {y^{b} } \right|}} \ge \rho_{ab}$$
    (13)

  • If not: Increment the vigilance parameter:

    $$\rho_{a} = \frac{{\left| {I^{e} \wedge w_{j}^{a} } \right|}}{{\left| {I^{e} } \right|}} + \varepsilon$$
    (14)

  • Reset: \(T_{j}^{a}\) = 0;

  • If Match Tracking is attended:

  • Resonance, adaptation of \(Fuzzy\,{\text{ART}}_{a}\) weights:

    $$w_{J}^{\text{new}} = \beta \left( {I^{e} \wedge w_{J}^{\text{old}} } \right) + \left( {1 - \beta } \right)w_{J}^{\text{old}}$$
    (15)

  • Update the Inter-ART module weights:

    $$W_{JK}^{ab} = \left[ {y_{1}^{ab} ,y_{2}^{ab} , \ldots ,y_{N}^{ab} } \right],{\text{where}}:$$
    $$y_{jk}^{ab} = \left\{ {\begin{array}{*{20}c} {1,} & {{\text{if}}\,j = J;\,k = K} \\ {0,} & {{\text{if}}\,j \ne J;\,k \ne K} \\ \end{array} } \right.$$
    (16)

  • Verify if all training pairs were processed;

  • If not: \(\rho_{a} = \rho_{a}^{\text{original}}\) and continue in \(Fuzzy\,{\text{ART}}_{a}\) and \(Fuzzy\,{\text{ART}}_{b} ;\)

  • If yes: end training.

  • where \(\alpha\): chosen parameter (\(\alpha\) > 0); \(\beta\): training rate [0, 1]; \(\rho_{a}\):vigilance parameter of \({\text{ART}}_{a}\) module (0, 1]; \(\rho_{b}\):vigilance parameter of \({\text{ART}}_{b}\) module (0, 1]; \(\rho_{ab}\):vigilance parameter of \({\text{ART}}_{ab}\) module (0, 1]; \(\varepsilon\): increment of parameter \(\rho_{a}\); n: quantity of input patterns.

The Match-Tracking allows the increase in the vigilance parameter \(\rho_{a}\) (\({\text{ART}}_{a}\) module) to correct the error in \({\text{ART}}_{b}\) module. Hence, when a wrong prognostic is performed, generalization is maximized, whereas an error is minimized. The \({\text{ART}}_{a}\) module begins the search for a correct prognostic, or a new category, that is created for the current input.

The Fuzzy ARTMAP ANN, used in this work, is implemented according to references [41,42,43,44]. Other studies, also apply architectures based on ARTMAP artificial neural networks, to predict electricity consumption at more aggregate levels [29, 31]. ARTMAP ANN is also applied to other forecasting tasks [45,46,47].

4 Singular spectrum analysis: SSA

The singular spectrum analysis is a powerful tool for time series analysis. This technique incorporates the elements of multivariate statistics, classical time series analysis, multivariate geometry, dynamical systems, and signal processing. SSA can decompose the original time series in a small number of components, such as the tendency with low frequency variation, oscillatory components, and white noise.

Hence, it can extract complex and nonlinear tendencies, detect changes in a regime, remove seasonality with variable amplitude and periods, and smoothen time series. The advantages of SSA include the fact that, in general, short univariate time series are sufficient to obtain good results, depends on a small number of parameters, requires only basic knowledge on the series from the analyst, has low computational cost and the denoised series does not present delay in comparison with the original series [48, 49]. Other studies also apply SSA as a data denoising method, for example references [50,51,52].

The SSA algorithm is divided in two steps: decomposition and reconstruction [48, 53, 54]. Each of these two steps evolves into two other sub-steps. Thus, the decomposition is formed by incorporating and decomposing in single values, whereas the reconstruction includes the clustering and diagonal averaging.

During the sub-step incorporation, let \(y_{t } \left( {t = 1, 2, 3, \ldots ,N} \right)\) be an N dimensional time series to be analyzed using SSA. \(y_{t}\) is transformed in a sequence of \(K\) L-dimension vectors \(\varvec{x}_{1} , \ldots , \varvec{x}_{\varvec{K}}\) (L being the size of the window), which are used to form the trajectory matrix \(X\) as

$$\varvec{X} = \left[ {\varvec{x}_{1} , \ldots , \varvec{x}_{\varvec{K}} } \right] = \left( {\begin{array}{*{20}l} {\varvec{y}_{1} } \hfill & {\varvec{y}_{2} } \hfill & \ldots \hfill & {\varvec{y}_{\varvec{K}} } \hfill \\ {\varvec{y}_{2} } \hfill & {\varvec{y}_{3} } \hfill & \ldots \hfill & {\varvec{y}_{{\varvec{K} + 1}} } \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {\varvec{y}_{\varvec{L}} } \hfill & {\varvec{y}_{{\varvec{L} + 1}} } \hfill & \ldots \hfill & {\varvec{y}_{\varvec{N}} } \hfill \\ \end{array} } \right)$$
(17)

This matrix has size \(L\) by \(K\), where \(K = N - L + 1\). \(L\) must be contained in the interval \(2 \le L \le N - 1\). A method to find the optimal value for the parameter \(L\) is still an open discussion in the literature.

The decomposition in single values consists of transforming the trajectory matrix in a sum of matrices with rank 1. Let \(S = XX^{T}\), \(\lambda_{1} , \lambda_{2} , \ldots ,\lambda_{L}\) be the respective eigenvalues in decreasing order, and \(U_{1} , U_{2} , \ldots , U_{L}\) be the eigenvectors associated to \(\lambda_{1} , \lambda_{2} , \ldots ,\lambda_{L}\). If \(V_{i} = X^{T} U_{i} /\sqrt {\lambda_{i} }\), the trajectory matrix \(X\) can be written as \(X = X_{1} + X_{2} + \ldots + X_{L}\), where \(X_{i} = \lambda_{i} U_{i} V_{i}^{T}\). The set \(\left( {\lambda_{i} , U_{i} , V_{i} } \right)\) is called the ith eigentriple of matrix \(X\).

The clustering sub-step combines the eigentriples, such that, the group with less variability is adopted as tendency, one or more components are described as oscillatory with variable periods and, finally, the last one, with higher variability, is considered random noise. Thus, the \(L\) eigentriples are separated into \(m\) disjoint sets. Let \(I = \left\{ {i_{1} , i_{2} , \ldots ,i_{p} } \right\},\) the eigentriples index group in one of the \(m\) desired subsets; therefore, the resulting matrix \(X_{I}\) is determined as the sum of the corresponding matrices \(X_{i}\), i.e., \(X_{I} = X_{{i_{1} }} + X_{{i_{2} }} + \cdots + X_{{i_{p} }}\).

The diagonal averaging sub-step transforms each of the \(m\) matrices \(X_{I}\) in a univariate time subseries of size \(N\), called an SSA component. If \(L^{*} = { \hbox{min} }\left( {L,K} \right)\), \(K^{*} = { \hbox{max} }\left( {L,K} \right)\), and \(y_{{I_{t} }} \left( {t = 1,2, \ldots ,N} \right)\) is an SSA component, each element of \(y_{{I_{t} }}\) is given by:

$$y_{{I_{t} }} \left\{ {\begin{array}{*{20}c} {\frac{{\mathop \sum \nolimits_{i = 1}^{t} x_{{I_{{\left( {i,t - i + 1} \right)}} }} }}{t}, \quad \forall 1 \le t < L^{*} } \\ {\frac{{\mathop \sum \nolimits_{i = 1}^{{L^{*} }} x_{{I_{{\left( {i,t - i + 1} \right)}} }} }}{{L^{*} }}, \quad \forall L^{*} \le t \le K^{*} } \\ {\frac{{\mathop \sum \nolimits_{{i = t - K^{*} }}^{{N - K^{*} }} x_{{I_{{\left( {i,t - i + 1} \right)}} }} }}{{N - K^{*} }}, \quad \forall K^{*} < t \le N} \\ \end{array} } \right.$$
(18)

This step consists of calculating the average of the elements \(X_{I}\), called \(x_{{I_{{\left( {i,j} \right)}} }}\), where \(i + j = t + 1\) In this expression, \(t\) equals 1 gives \(y_{{I_{1} }} = x_{{I_{{\left( {1,1} \right)}} }}\), for \(t\) equals 2 then \(y_{{I_{2} }} = \frac{{x_{{I_{{\left( {1,2} \right)}} }} + x_{{I_{{\left( {2,1} \right)}} }} }}{2}\), and so on.

5 Methodology

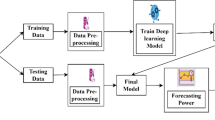
In summary, the methodology used in this paper consists in denoising the time series with SSA and, after that, using the denoised series as training set for the Fuzzy ARTMAP ANN which will then provide the forecast. Herein each step will be detailed.

5.1 SSA decomposition

This step and the next one consist in applying the methodology described in the SSA—singular spectrum analysis section of this paper.

SSA is used to reduce the noise level of the series by ignoring the component classified as noise when reconstructing. The only relevant parameter for this step of the method is the window length, set as two times the data periodicity in this work. According to [22, 48], using window lengths multiple of periodicity attains better separability of the data. In this step, just the data prior to the forecasting horizon was used.

5.2 Hierarchical clustering of SSA components and reconstruction

In this work, the SSA components are hierarchically clustered in three groups using the weighted-correlations matrix as distance criterion. Such groups are interpreted as the trend, the oscillatory components and noise, which are not considered when the smoothed series is reconstructed.

5.3 Fuzzy ARTMAP training and parameter optimization

Following that, the rebuilt series is presented to the Fuzzy ARTMAP ANN for training, as data to be forecasted was not included in the previous step, the training set does not contain the period to be forecasted. The Fuzzy ARTMAP ANN parameters were chosen considering appropriate values [43, 55, 56], the parameters \(\rho_{a}\), \(\rho_{b}\), and \(\alpha\) were fine tuned by a grid search, and the search is realized between values 0.93 and 0.97, 0.995 and 0.999, and 0.003 and 1.323, respectively, with variations of 0.01 for \(\rho_{a}\), 0.001 for \(\rho_{b}\), and 0.66 for \(\alpha\). The parameters \(\beta\) and \(\rho_{ab}\) were set to 1 and were not changed. The dimension of the input vectors used for the prediction phase is defined according to the results obtained during the validation phase, where tests were done for 1–7 days. Mean absolute percent error (MAPE) is the criterion for parameter selection and the lower value is chosen.

The figure below illustrates the described method (Fig. 3).

Fig. 3
figure 3

Fuzzy ARTMAP ANN flowchart

Full size image

To test the efficiency of the proposal, two well-known methods are used as benchmark: the SARIMA models and the feedforward MLP, with training done using the backpropagation algorithm [40]. The time series is forecasted with and without noise using SSA. The training set, for both the benchmarks and the Fuzzy ARTMAP ANN, was composed by the available data prior to the forecast horizon.

For choosing the SARIMA model order and calculating the coefficients, the automatic method described by [57] was used. This method is implemented by the auto.arima function of the R language forecast package.

The feedforward MLP weight calculations were made utilizing the mlp function of the RSNNS package, also available for the R language. Just one hidden layer with sigmoid activation function was used, as it is sufficient for the majority of the forecasting problems [58]. In the output layer just one neuron with linear activation function was used, the multi-step forecast is made iteratively, presenting the output of the previous step as an input for the next one. The number of neurons in the input and hidden layers was chosen by testing various architectures, and selecting the one that presented the minimal in-sample MAPE. For the input layer, the number of neurons tested was \(n = ks\), \(n = ks + 2\) or \(n = ks - 2\), where \(n\) is the number of neurons in the input layer, \(k\) an natural number lower than 5, and \(s\) the seasonality of the time series. The number of neurons in the hidden layer was a natural number greater than \(\frac{n}{2} - 3\) and lower than \(\frac{n}{2} + 3\).

The results were also compared with those provided by Fuzzy ARTMAP ANN without using the SSA. The forecast horizons are for 1, 3 and 7 days for all methods.

5.4 Performance evaluation

MAPE is used to evaluate the performance of the forecasts, according to Eq. 19:

$${\text{MAPE}} = \frac{1}{{n_{e} }}\mathop \sum \limits_{t = 1}^{{n_{e} }} \frac{{\left| {L_{t} - \underline{{F_{t} }} } \right|}}{{L_{t} }} \times 100$$
(19)

where \(L_{t}\): real electrical load at time \(t\); \(\underline{{F_{t} }}\): forecasted electrical load at time \(t\);

ne: quantity of inputs presented for the diagnosis phase.

In this paper, MAPE was used with the main purpose of measuring the forecast quality from the several methods. Aiming this, all the time series were split into two different sets, one for training and another for testing. The test set was not used for modeling, and was the reference in the forecasts MAPE calculations, being compared with the forecasts.

MAPE is one of the most popular measures of forecast accuracy, is scale-independent and easy to interpret, making it popular in the industrial sector, including the electrical energy companies, where it is a pattern to evaluate the performance of load forecasting [59, 60]. MAPE is recommended in most textbooks [61, 62]. Lower MAPE numbers indicate a more accurate result [63].

MAPE is not indicated when the real values are zero or close to zero. This situation is not verified in the data set used in this paper.

6 Results

Table 1 presents the MAPE scores for the forecasts provided by each method, for the series with 48 daily data using three different predictive horizons, 1, 3 and 7 days, Table 2, in its turn, shows the MAPEs calculated using the same methods and horizons, but for the series with 96 daily data. Bold values represent the best MAPE for each predictive horizon.

Table 1 MAPE of the predictions for load curve with 48 daily data
Full size table
Table 2 MAPE of the predictions for load curve with 96 daily data
Full size table

The performance of the Fuzzy ARTMAP ANN was improved by noise removal, reducing the MAPE indicator in all scenarios. In addition, it can be perceived that for the horizons of 3 and 7 days, no method had a superior performance in MAPE terms and, for the 1 day horizon, only SARIMA presented a smaller indicator.

Table 2 shows a similar scenario, being Fuzzy ARTMAP ANN plus SSA combination the method capable of providing the most assertive forecasts for the 3 and 7 days horizons. This demonstrates the power of maintenance of generalization capacity of this kind of ANN, even for larger forecasts horizons.

When comparing the two artificial neural network architectures used in this article, feedforward MLP and Fuzzy ARTMAP, it is not possible to generalize the statement that ANNs behave better in this type of scenario, since among all the models tested, feedforward MLP had some of the worst results, while Fuzzy ARTMAP ANN presented most of the best. Furthermore, it is also not possible to say if statistical or artificial intelligence methods are superior, since SARIMA obtained the best results in some of the scenarios.

Considering all the tested scenarios, ARTMAP Fuzzy ANN proved to be the most consistent predictor, since its results varied very little in all different scenarios, attesting to the robustness of the method. In addition, in various cases, the MAPE of the ARTMAP Fuzzy ANN was the best, showing its capacity in providing assertive results.

Figure 4 shows the performance of the three methods for 7 days in advance, where the load curve contains 96 measures. Considering this scenario, it is important to highlight that only the Fuzzy ARTMAP ANN is able to represent the real load shape, discerning labor days from weekends without any previous knowledge inserted by the researcher. By just extracting information from the data, it has the potential of being very useful when this kind of information is not available for the analyst.

Fig. 4
figure 4

Seven days in advance forecast (daily curve with 96 measures) without noise removal

Full size image

7 Conclusions

The use of the Fuzzy ARTMAP ANN with noise removal by SSA presents the best results when compared to other methods considered as the benchmark in literature, except for the results for a horizon of 1 day.

It is emphasized that the modeling is difficult due to the nature of the data. This occurs according to the aggregation level and the presence of atypical days in the series. The former causes a relative increase in randomness of the model, thereby increasing the amplitude of the noise due to unpredictable decisions. The latter is due to the fact that classical modeling methodologies, very often, do not capture such characteristics and are not prepared to incorporate previous knowledge to the forecasts. In this situation, Fuzzy ARTMAP ANN presents superior performance and, when enhanced with the use of the SSA, provides more generalization.

The use of noise removal with the other methods presents ambiguous results; however, for the load curves formed by 48 data, the results are promising, according to the MAPE for the 3 days and 7 days horizon. Nevertheless, the results for 7 days in advance must be carefully analyzed considering the presence of labor days and weekends in the interval of prediction. SARIMA and feedforward MLP cannot adapt to this situation; therefore, their prediction capacity is reduced, and noise removal does not matter.

The good results obtained by SARIMA for 1 day in advance are due to the behavior correlated with the previous days, consequently providing a good approximation by linear combination, which is characteristic of this model.

8 Future works

In future work, the authors will continue to incorporate data preprocessing as well as including previous information to the forecast methods. One approach is to cluster the data according to the nature of the days, and then use a specific model for each subset.