Hostname: page-component-848d4c4894-p2v8j Total loading time: 0.001 Render date: 2024-06-02T03:31:16.523Z Has data issue: false hasContentIssue false
  • English
  • Français

EXISTENCE AND STABILITY OF PERIODIC SOLUTIONS OF A RAYLEIGH TYPE EQUATION

Part of: Qualitative theory

Published online by Cambridge University Press:  17 April 2009

YONG WANG  and
XIAN-ZHI DAI
YONG WANG*
Affiliation:
School of Sciences, Southwest Petroleum University, Chengdu, Sichuan 610500, People’s Republic of China (email: odinswang@yahoo.com.cn, higher80@163.com)
XIAN-ZHI DAI
Affiliation:
School of Electronics and Information Engineering, Southwest Petroleum University, Chengdu, Sichuan 610500, People’s Republic of China
*
✉For correspondence; e-mail: odinswang@yahoo.com.cn, higher80@163.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this work, we shall be concerned with the following forced Rayleigh type equation: 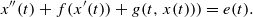Under certain assumptions, some criteria for guaranteeing the existence, uniqueness and asymptotic stability (in the Lyapunov sense) of periodic solutions of this equation are presented by applying the Manásevich–Mawhin continuation theorem, Floquet theory, Lyapunov stability theory and some analysis techniques. Moreover, an example is provided to demonstrate the applications of our results.

Keywords

Rayleigh equationperiodic solutionexistenceuniquenessstability

MSC classification

Secondary: 34C25: Periodic solutions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 79 , Issue 3 , June 2009 , pp. 377 - 390
Copyright
Copyright © Australian Mathematical Society 2009

Footnotes

This work is supported by SWPU Science and Technology Fund, China.

References

[1] Chen, H. and Li, Y., ‘Rate of decay of stable periodic solutions of Duffing equations’, J. Differential Equations 236 (2007), 493–503.CrossRefGoogle Scholar
[2] Coddington, E. A. and Levinson, N., Theory of Ordinary Differential Equations (McGraw-Hill, New York, 1955).Google Scholar
[3] Fletcher, N. H., ‘Autonomous vibration of simple pressure-controlled valves in gas flows’, J. Acoust. Soc. Am. 93 (1993), 2172–2180.CrossRefGoogle Scholar
[4] Gaines, R. and Mawhin, J., Coincidence Degree, and Nonlinear Differential Equations, Lecture Notes in Mathematics, 568 (Springer, Berlin, 1977).CrossRefGoogle Scholar
[5] Hardy, G. H., Littlewood, J. E. and Pólya, G., Inequalities (Cambridge University Press, London, 1964).Google Scholar
[6] Keith, W. L. and Rand, R. H., ‘Dynamics of a system exhibiting the global bifurcation of a limit cycle at infinity’, Int. J. Nonlinear. Mech. 20 (1985), 325–338.CrossRefGoogle Scholar
[7] Lazer, A. C. and McKenna, P. J., ‘On the existence of stable periodic solutions of differential equations of Duffing type’, Proc. Amer. Math. Soc. 110 (1990), 125–133.CrossRefGoogle Scholar
[8] Li, Y. and Huang, L., ‘New results of periodic solutions for forced Rayleigh-type equations’, J. Comput. Appl. Math. 221 (2008), 98–105.CrossRefGoogle Scholar
[9] Lu, S. and Ge, W., ‘Some new results on the existence of periodic solutions to a kind of Rayleigh equation with a deviating argument’, Nonlinear Anal. 56 (2004), 501–514.CrossRefGoogle Scholar
[10] Lu, S., Ge, W. and Zheng, Z., ‘Periodic solutions for a kind of Rayleigh equation with a deviating argument’, Appl. Math. Lett. 17 (2004), 443–449.CrossRefGoogle Scholar
[11] Manásevich, R. and Mawhin, J., ‘Periodic solutions for nonlinear systems with p-Laplacian-like operators’, J. Differential Equations 145 (1998), 367–393.CrossRefGoogle Scholar
[12] Mawhin, J., ‘Periodic solutions of some vector retarded functional differential equations’, J. Math. Anal. Appl. 45 (1974), 588–603.CrossRefGoogle Scholar
[13] Ortega, R., ‘Stability and index of periodic solutions of an equation of Duffing type’, Boll. Unione Mat. Ital. Sez. B Artic. Ric. Mat. (7) 3 (1989), 533–546.Google Scholar
[14] Shimizu, T., ‘Limit cycles and constants of motion in dissipative systems’, Phys. Lett. A 69 (1979), 379–381.CrossRefGoogle Scholar
[15] Shimizu, T. and Morioka, N., ‘Chaos and limit cycles in the Lorenz model’, Phys. Lett. A 66 (1978), 182–184.CrossRefGoogle Scholar
[16] Strutt [Lord Rayleigh], J. W., Theory of Sound, Volume 1 (Dover Publications, New York, 1877), reissued 1945.Google Scholar
[17] Wang, G. Q. and Cheng, S. S., ‘A priori bounds for periodic solutions of a delay Rayleigh equation’, Appl. Math. Lett. 12 (1999), 41–44.CrossRefGoogle Scholar
[18] Zhou, Y. and Tang, X., ‘On existence of periodic solutions of Rayleigh equation of retarded type’, J. Comput. Appl. Math. 203 (2007), 1–5.CrossRefGoogle Scholar